2024-2025学年山东省淄博市沂源县七年级(上)期中数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市沂源县七年级(上)期中数学试卷(五四学制)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 397.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 18:07:23 | ||
图片预览


文档简介
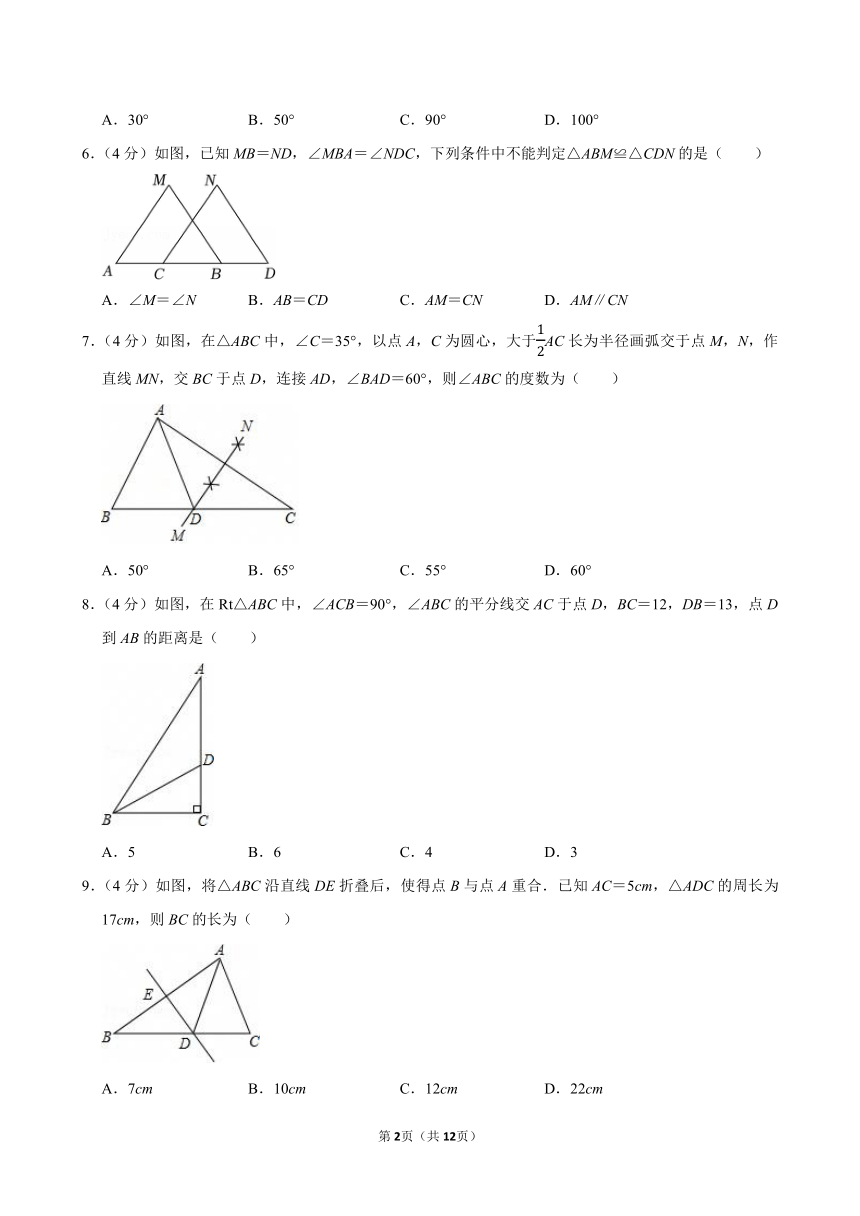
2024-2025学年山东省淄博市沂源县七年级(上)期中数学试卷(五四学制)
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(4分)下列图中不是轴对称图形的是( )
A. B. C. D.
2.(4分)下列图形中,对称轴数量最多的是( )
A. B. C. D.
3.(4分)人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
4.(4分)在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a﹣b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.不是直角三角形
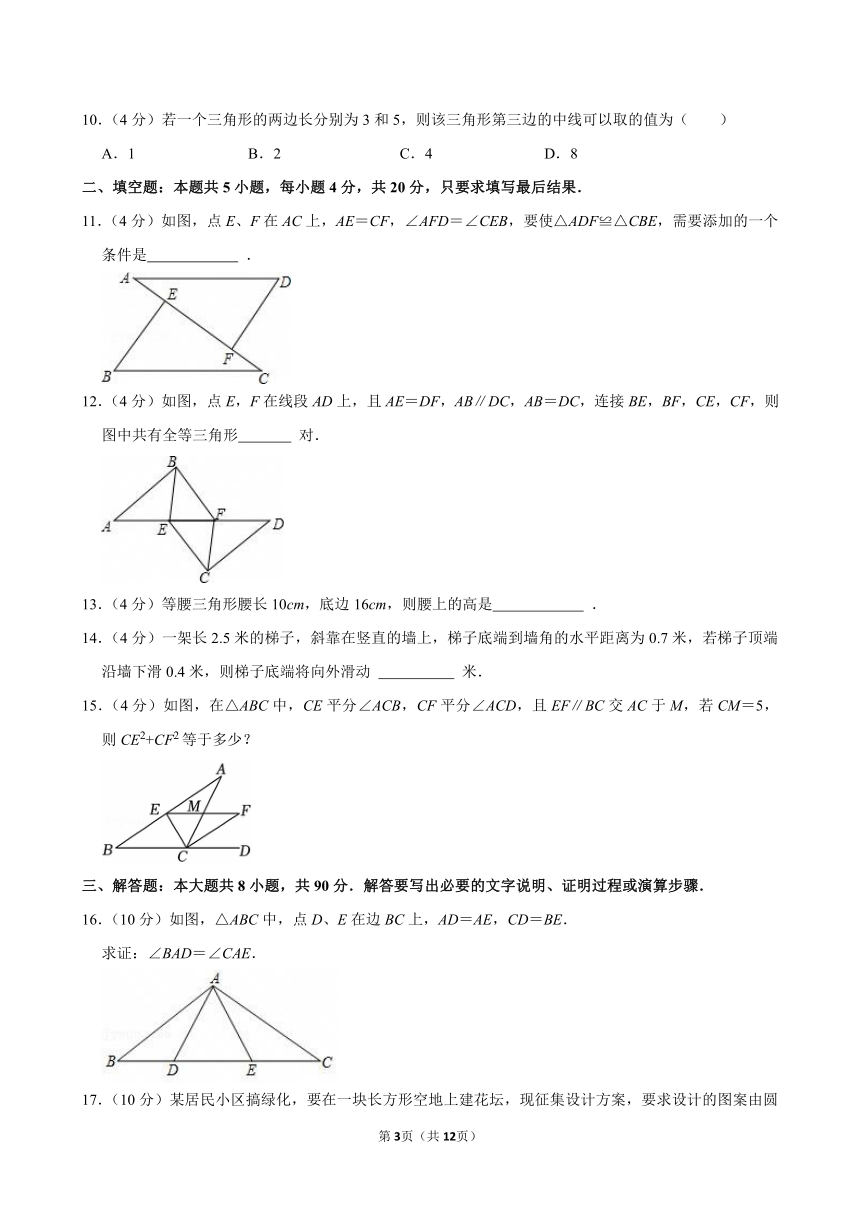
5.(4分)如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.(4分)如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
7.(4分)如图,在△ABC中,∠C=35°,以点A,C为圆心,大于AC长为半径画弧交于点M,N,作直线MN,交BC于点D,连接AD,∠BAD=60°,则∠ABC的度数为( )
A.50° B.65° C.55° D.60°
8.(4分)如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )
A.5 B.6 C.4 D.3
9.(4分)如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm B.10cm C.12cm D.22cm
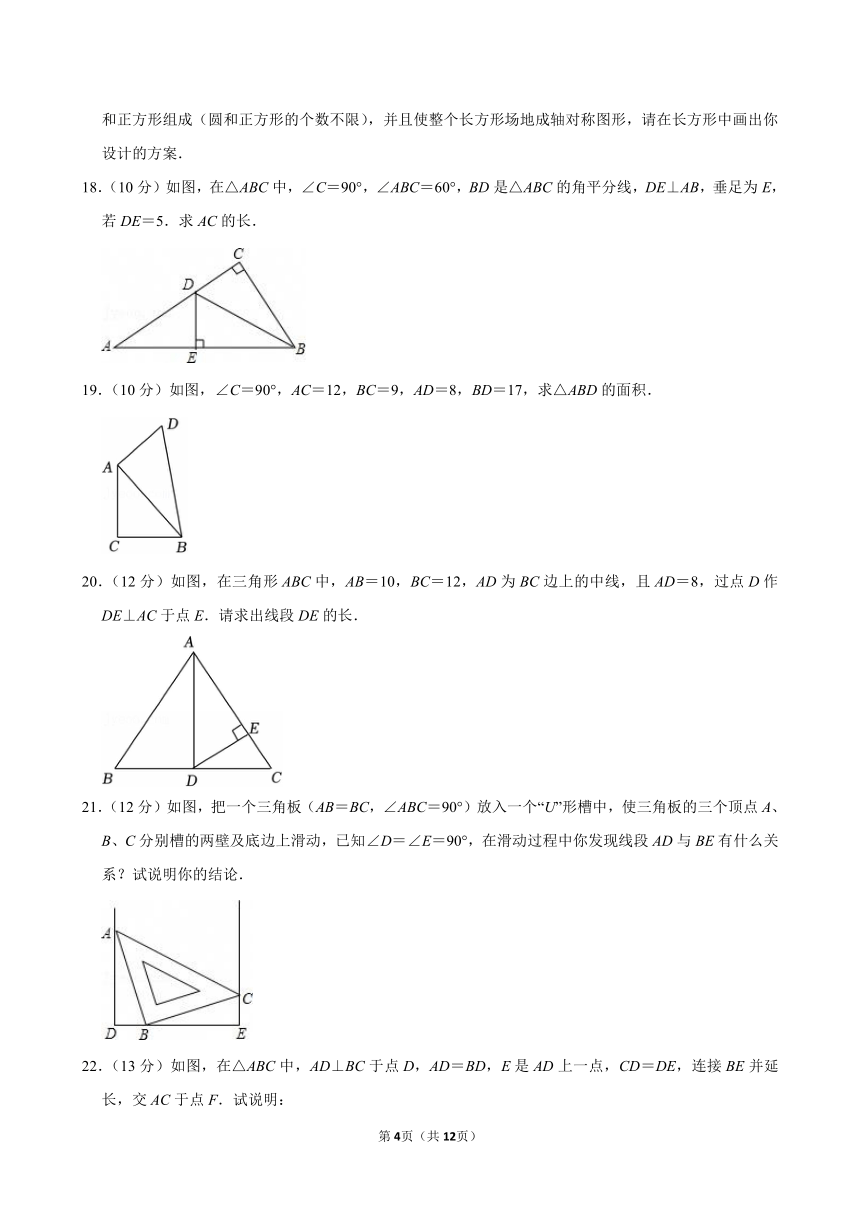
10.(4分)若一个三角形的两边长分别为3和5,则该三角形第三边的中线可以取的值为( )
A.1 B.2 C.4 D.8
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
11.(4分)如图,点E、F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是 .
12.(4分)如图,点E,F在线段AD上,且AE=DF,AB∥DC,AB=DC,连接BE,BF,CE,CF,则图中共有全等三角形 对.
13.(4分)等腰三角形腰长10cm,底边16cm,则腰上的高是 .
14.(4分)一架长2.5米的梯子,斜靠在竖直的墙上,梯子底端到墙角的水平距离为0.7米,若梯子顶端沿墙下滑0.4米,则梯子底端将向外滑动 米.
15.(4分)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于多少?
三、解答题:本大题共8小题,共90分.解答要写出必要的文字说明、证明过程或演算步骤.
16.(10分)如图,△ABC中,点D、E在边BC上,AD=AE,CD=BE.
求证:∠BAD=∠CAE.
17.(10分)某居民小区搞绿化,要在一块长方形空地上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆和正方形的个数不限),并且使整个长方形场地成轴对称图形,请在长方形中画出你设计的方案.
18.(10分)如图,在△ABC中,∠C=90°,∠ABC=60°,BD是△ABC的角平分线,DE⊥AB,垂足为E,若DE=5.求AC的长.
19.(10分)如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
20.(12分)如图,在三角形ABC中,AB=10,BC=12,AD为BC边上的中线,且AD=8,过点D作DE⊥AC于点E.请求出线段DE的长.
21.(12分)如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、B、C分别槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中你发现线段AD与BE有什么关系?试说明你的结论.
22.(13分)如图,在△ABC中,AD⊥BC于点D,AD=BD,E是AD上一点,CD=DE,连接BE并延长,交AC于点F.试说明:
(1)BE=AC;
(2)BF⊥AC.
23.(13分)如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点D在BC上,连接
CE.
(1)△ABD≌△ACE吗?请说明理由;
(2)若DF⊥AC,点F在线段CE上,且CF=2,FE=3,求BC的长.
2024-2025学年山东省淄博市沂源县七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D A D C A A C B
1.解:A、有四条对称轴,是轴对称图形,故本选项错误;
B、有三条对称轴,是轴对称图形,故本选项错误;
C、不是轴对称图形,因为找不到任何这样的一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义,故本选项正确;
D、有二条对称轴,是轴对称图形,故本选项错误.
故选:C.
2.解:A、正方形的对称轴为4条,故此选项不合题意;
B、正六边形的对称轴为6条,故此选项符合题意;
C、该图形的对称轴为3条,故此选项不合题意;
D、该图形的对称轴为4条,故此选项不合题意;
故选:B.
3.解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
4.解:∵(a+b)(a﹣b)=c2,
∴a2﹣b2=c2,即c2+b2=a2,故此三角形是直角三角形,a为直角三角形的斜边,
∴∠A为直角.
故选:A.
5.解:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°﹣∠A﹣∠C=180°﹣50°﹣30°=100°.
故选:D.
6.解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;
B、AB=CD,符合SAS,能判定△ABM≌△CDN,故B选项不符合题意;
C、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故C选项符合题意;
D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.
故选:C.
7.解:由作图可知MN是AC的垂直平分线,
∴DA=DC,
则∠DAC=∠C=35°,
∵∠BAD=60°,
∴∠B=180°﹣∠BAD﹣∠DAC﹣∠C
=180°﹣60°﹣35°﹣35°
=50°,
故选:A.
8.解:作DE⊥AB于E,
∵∠ACB=90°,BC=12,DB=13,
∴CD5,
∵BD是∠ABC的平分线,∠ACB=90°,DE⊥AB,
∴DE=CD=5,
故选:A.
9.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD,
∴BD+CD=12cm.
即BC=12cm,
故选:C.
10.解:如图所示,AB=3,AC=5,
设BC=2a,AD=x,
延长AD至E,使AD=DE,
在△BDE与△CDA中,
∵AD=DE,BD=CD,∠ADC=∠BDE,
∴△BDE≌△CDA,
∴AE=2x,BE=AC=5,
在△ABE中,
∵BE﹣AB<AE<AB+BE,即5﹣3<2x<3+5,
∴1<x<4.
故选:B.
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
11.解:
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵∠AFD=∠CEB,
∴可添加∠A=∠C,
在△ADF和△CEB中
∴△ADF≌△CEB(AAS),
故答案为:∠A=∠C.
12.解:图中全等三角形有:△BAF≌△CDE,△BAE≌△CDF,△BEF≌△CFE,共3对,
故答案为:3.
13.解:作AD⊥BC于D,
∵AB=AC,
∴BD=BC=8cm,
∴AD6cm,
∴S△ABCBC AD=48cm2,
腰上的高是48×2÷10=9.6cm.
故答案为:9.6cm.
14.解:由题意可得:AB=2.5m,AO=0.7m,
故BO2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向外滑动0.8m,
故答案为:0.8.
15.解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE∠ACB,∠ACF∠ACD,即∠ECF(∠ACB+∠ACD)=90°
∴△EFC为直角三角形,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=5,EF=10,
由勾股定理可知CE2+CF2=EF2=100.
三、解答题:本大题共8小题,共90分.解答要写出必要的文字说明、证明过程或演算步骤.
16.证明:∵AD=AE,
∴∠ADE=∠AED,
在△ADC和△AEB中,
,
∴△ADC≌△AEB(SAS),
∴∠BAE=∠DAC,
∴∠BAD=∠CAE.
17.解:如图所示:(答案不唯一)
18.解:∵BD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=5,
∵∠C=90°,∠ABC=60°,
∴∠A=90°﹣60°=30°,
∴AD=2DE=2×5=10,
∴AC=AD+CD=10+5=15.
19.解:∵∠C=90°,AC=12,BC=9,
∴AB2=AC2+CB2,
∴AB=15.
∵AD=8,BD=17,
∴DB2=AD2+AB2,
∴∠DAB=90°,
∴△ABD的面积AB×AD=60.
答:△ABD的面积为60.
20.解:∵BC=12,AD为BC边上的中线,
∴BD=DCBC=6,
∵AD=8,AB=10,
∴BD2+AD2=AB2,
∴∠ADB=90°,
即AD⊥BC;
∵AD⊥BC,AD为BC边上的中线,
∴AB=AC,
∵AB=10,
∴AC=10,
∵△ADC的面积SAD DCAC DE
∴,
解得:DE=4.8.
21.解:AD=BE,AD⊥BE.
理由如下:
∵∠D=90°,
∴∠ABD+∠BAD=90°
又∵∠ABC=90°,
∴∠ABD+∠EBC=90°
∴∠BAD=∠EBC;
又∵AB=BC,∠D=∠E;
∴△ABD≌△BCE(AAS);
∴AD=BE,AD⊥BE.
22.证明:(1)∵AD⊥BC,
∴∠ADC=∠BDE=90°,
在△ACD和△BED中
,
∴△ACD≌△BED(SAS),
∴BE=AC;
(2)由(1)可得∠CAD=∠CBF,
∵∠C+∠CAD=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴BF⊥AC.
23.(1)证明:△ABD≌△ACE,
理由:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵在△ABD和△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:
∵△ABD≌△ACE,
∴∠B=∠ACE,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACB=∠ACE,
∵在△CGD和△CGF中,,
∴△CGD≌△CGF,(ASA)
∴CF=CD,
∴BC=BD+CD=CE+CF=CF+EF+CF=7.
第2页(共2页)
一、选择题:本大题共10个小题,每小题4分,共40分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(4分)下列图中不是轴对称图形的是( )
A. B. C. D.
2.(4分)下列图形中,对称轴数量最多的是( )
A. B. C. D.
3.(4分)人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
4.(4分)在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a﹣b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.不是直角三角形
5.(4分)如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.(4分)如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
7.(4分)如图,在△ABC中,∠C=35°,以点A,C为圆心,大于AC长为半径画弧交于点M,N,作直线MN,交BC于点D,连接AD,∠BAD=60°,则∠ABC的度数为( )
A.50° B.65° C.55° D.60°
8.(4分)如图,在Rt△ABC中,∠ACB=90°,∠ABC的平分线交AC于点D,BC=12,DB=13,点D到AB的距离是( )
A.5 B.6 C.4 D.3
9.(4分)如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm B.10cm C.12cm D.22cm
10.(4分)若一个三角形的两边长分别为3和5,则该三角形第三边的中线可以取的值为( )
A.1 B.2 C.4 D.8
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
11.(4分)如图,点E、F在AC上,AE=CF,∠AFD=∠CEB,要使△ADF≌△CBE,需要添加的一个条件是 .
12.(4分)如图,点E,F在线段AD上,且AE=DF,AB∥DC,AB=DC,连接BE,BF,CE,CF,则图中共有全等三角形 对.
13.(4分)等腰三角形腰长10cm,底边16cm,则腰上的高是 .
14.(4分)一架长2.5米的梯子,斜靠在竖直的墙上,梯子底端到墙角的水平距离为0.7米,若梯子顶端沿墙下滑0.4米,则梯子底端将向外滑动 米.
15.(4分)如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于多少?
三、解答题:本大题共8小题,共90分.解答要写出必要的文字说明、证明过程或演算步骤.
16.(10分)如图,△ABC中,点D、E在边BC上,AD=AE,CD=BE.
求证:∠BAD=∠CAE.
17.(10分)某居民小区搞绿化,要在一块长方形空地上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆和正方形的个数不限),并且使整个长方形场地成轴对称图形,请在长方形中画出你设计的方案.
18.(10分)如图,在△ABC中,∠C=90°,∠ABC=60°,BD是△ABC的角平分线,DE⊥AB,垂足为E,若DE=5.求AC的长.
19.(10分)如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
20.(12分)如图,在三角形ABC中,AB=10,BC=12,AD为BC边上的中线,且AD=8,过点D作DE⊥AC于点E.请求出线段DE的长.
21.(12分)如图,把一个三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角板的三个顶点A、B、C分别槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中你发现线段AD与BE有什么关系?试说明你的结论.
22.(13分)如图,在△ABC中,AD⊥BC于点D,AD=BD,E是AD上一点,CD=DE,连接BE并延长,交AC于点F.试说明:
(1)BE=AC;
(2)BF⊥AC.
23.(13分)如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点D在BC上,连接
CE.
(1)△ABD≌△ACE吗?请说明理由;
(2)若DF⊥AC,点F在线段CE上,且CF=2,FE=3,求BC的长.
2024-2025学年山东省淄博市沂源县七年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D A D C A A C B
1.解:A、有四条对称轴,是轴对称图形,故本选项错误;
B、有三条对称轴,是轴对称图形,故本选项错误;
C、不是轴对称图形,因为找不到任何这样的一条直线,使它沿这条直线折叠后,直线两旁的部分能够重合,即不满足轴对称图形的定义,故本选项正确;
D、有二条对称轴,是轴对称图形,故本选项错误.
故选:C.
2.解:A、正方形的对称轴为4条,故此选项不合题意;
B、正六边形的对称轴为6条,故此选项符合题意;
C、该图形的对称轴为3条,故此选项不合题意;
D、该图形的对称轴为4条,故此选项不合题意;
故选:B.
3.解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
4.解:∵(a+b)(a﹣b)=c2,
∴a2﹣b2=c2,即c2+b2=a2,故此三角形是直角三角形,a为直角三角形的斜边,
∴∠A为直角.
故选:A.
5.解:∵△ABC和△A′B′C′关于直线l对称,∠A=50°,∠C′=30°,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=30°,
∴∠B=180°﹣∠A﹣∠C=180°﹣50°﹣30°=100°.
故选:D.
6.解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;
B、AB=CD,符合SAS,能判定△ABM≌△CDN,故B选项不符合题意;
C、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故C选项符合题意;
D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.
故选:C.
7.解:由作图可知MN是AC的垂直平分线,
∴DA=DC,
则∠DAC=∠C=35°,
∵∠BAD=60°,
∴∠B=180°﹣∠BAD﹣∠DAC﹣∠C
=180°﹣60°﹣35°﹣35°
=50°,
故选:A.
8.解:作DE⊥AB于E,
∵∠ACB=90°,BC=12,DB=13,
∴CD5,
∵BD是∠ABC的平分线,∠ACB=90°,DE⊥AB,
∴DE=CD=5,
故选:A.
9.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD,
∴BD+CD=12cm.
即BC=12cm,
故选:C.
10.解:如图所示,AB=3,AC=5,
设BC=2a,AD=x,
延长AD至E,使AD=DE,
在△BDE与△CDA中,
∵AD=DE,BD=CD,∠ADC=∠BDE,
∴△BDE≌△CDA,
∴AE=2x,BE=AC=5,
在△ABE中,
∵BE﹣AB<AE<AB+BE,即5﹣3<2x<3+5,
∴1<x<4.
故选:B.
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
11.解:
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵∠AFD=∠CEB,
∴可添加∠A=∠C,
在△ADF和△CEB中
∴△ADF≌△CEB(AAS),
故答案为:∠A=∠C.
12.解:图中全等三角形有:△BAF≌△CDE,△BAE≌△CDF,△BEF≌△CFE,共3对,
故答案为:3.
13.解:作AD⊥BC于D,
∵AB=AC,
∴BD=BC=8cm,
∴AD6cm,
∴S△ABCBC AD=48cm2,
腰上的高是48×2÷10=9.6cm.
故答案为:9.6cm.
14.解:由题意可得:AB=2.5m,AO=0.7m,
故BO2.4(m),
∵梯子顶端沿墙下滑0.4m,
∴DO=2m,CD=2.5m,
∴CO=1.5m,
∴AC=CO﹣AO=1.5﹣0.7=0.8(m).
答:梯子底端将向外滑动0.8m,
故答案为:0.8.
15.解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE∠ACB,∠ACF∠ACD,即∠ECF(∠ACB+∠ACD)=90°
∴△EFC为直角三角形,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=5,EF=10,
由勾股定理可知CE2+CF2=EF2=100.
三、解答题:本大题共8小题,共90分.解答要写出必要的文字说明、证明过程或演算步骤.
16.证明:∵AD=AE,
∴∠ADE=∠AED,
在△ADC和△AEB中,
,
∴△ADC≌△AEB(SAS),
∴∠BAE=∠DAC,
∴∠BAD=∠CAE.
17.解:如图所示:(答案不唯一)
18.解:∵BD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=5,
∵∠C=90°,∠ABC=60°,
∴∠A=90°﹣60°=30°,
∴AD=2DE=2×5=10,
∴AC=AD+CD=10+5=15.
19.解:∵∠C=90°,AC=12,BC=9,
∴AB2=AC2+CB2,
∴AB=15.
∵AD=8,BD=17,
∴DB2=AD2+AB2,
∴∠DAB=90°,
∴△ABD的面积AB×AD=60.
答:△ABD的面积为60.
20.解:∵BC=12,AD为BC边上的中线,
∴BD=DCBC=6,
∵AD=8,AB=10,
∴BD2+AD2=AB2,
∴∠ADB=90°,
即AD⊥BC;
∵AD⊥BC,AD为BC边上的中线,
∴AB=AC,
∵AB=10,
∴AC=10,
∵△ADC的面积SAD DCAC DE
∴,
解得:DE=4.8.
21.解:AD=BE,AD⊥BE.
理由如下:
∵∠D=90°,
∴∠ABD+∠BAD=90°
又∵∠ABC=90°,
∴∠ABD+∠EBC=90°
∴∠BAD=∠EBC;
又∵AB=BC,∠D=∠E;
∴△ABD≌△BCE(AAS);
∴AD=BE,AD⊥BE.
22.证明:(1)∵AD⊥BC,
∴∠ADC=∠BDE=90°,
在△ACD和△BED中
,
∴△ACD≌△BED(SAS),
∴BE=AC;
(2)由(1)可得∠CAD=∠CBF,
∵∠C+∠CAD=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°,
∴BF⊥AC.
23.(1)证明:△ABD≌△ACE,
理由:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵在△ABD和△ACE中,
∴△ABD≌△ACE(SAS);
(2)解:
∵△ABD≌△ACE,
∴∠B=∠ACE,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACB=∠ACE,
∵在△CGD和△CGF中,,
∴△CGD≌△CGF,(ASA)
∴CF=CD,
∴BC=BD+CD=CE+CF=CF+EF+CF=7.
第2页(共2页)
同课章节目录
