广东省深圳市2025年九年级下学期中考模拟数学练习卷(二)(含答案)
文档属性
| 名称 | 广东省深圳市2025年九年级下学期中考模拟数学练习卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 18:11:21 | ||
图片预览




文档简介
2025年九年级第二学期深圳中考数学练习卷(二)
说明:本卷共6页,考试时间90分钟,满分100分,题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码.考试结束后,请将本卷和题卡一并上交.
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.位于贵州的“中国天眼”是500米口径球面射电望远镜,简称,是世界上最大的单口径球面射电望远镜(如图所示),它的俯视图是( )
A. B.C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
4.如图,点P是的重心.过P作的平行线,分别交,于点D,E;作交于点F.若的面积为18,则四边形的面积为( )
A.6 B.8 C.10 D.12
5.化学实验室有四种溶液:分别是氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,从中随机取出两种适量溶液,充分混合,有气体生成的概率是( )
A. B. C. D.
6.我国古代数学名著《张丘建算经》中记载:“今有甲、乙怀钱,各不知其数,甲得乙十钱多乙余钱五倍,乙得甲十钱适等,问甲、乙怀钱各几何 ”译文为:现有甲、乙两人带有一些银子,都不知道数量,甲得到乙的10两银子,甲比乙多出的银子是乙的5倍,乙得到甲的10两银子,两人的银子恰好相等,问甲、乙各带了多少两银子 设甲带了两银子,乙带了两银子,那么可列方程组为( )
A. B.
C. D.
7.如图,四边形与四边形都是菱形,点E,F在上,已知,,则的值为( )
A. B. C. D.
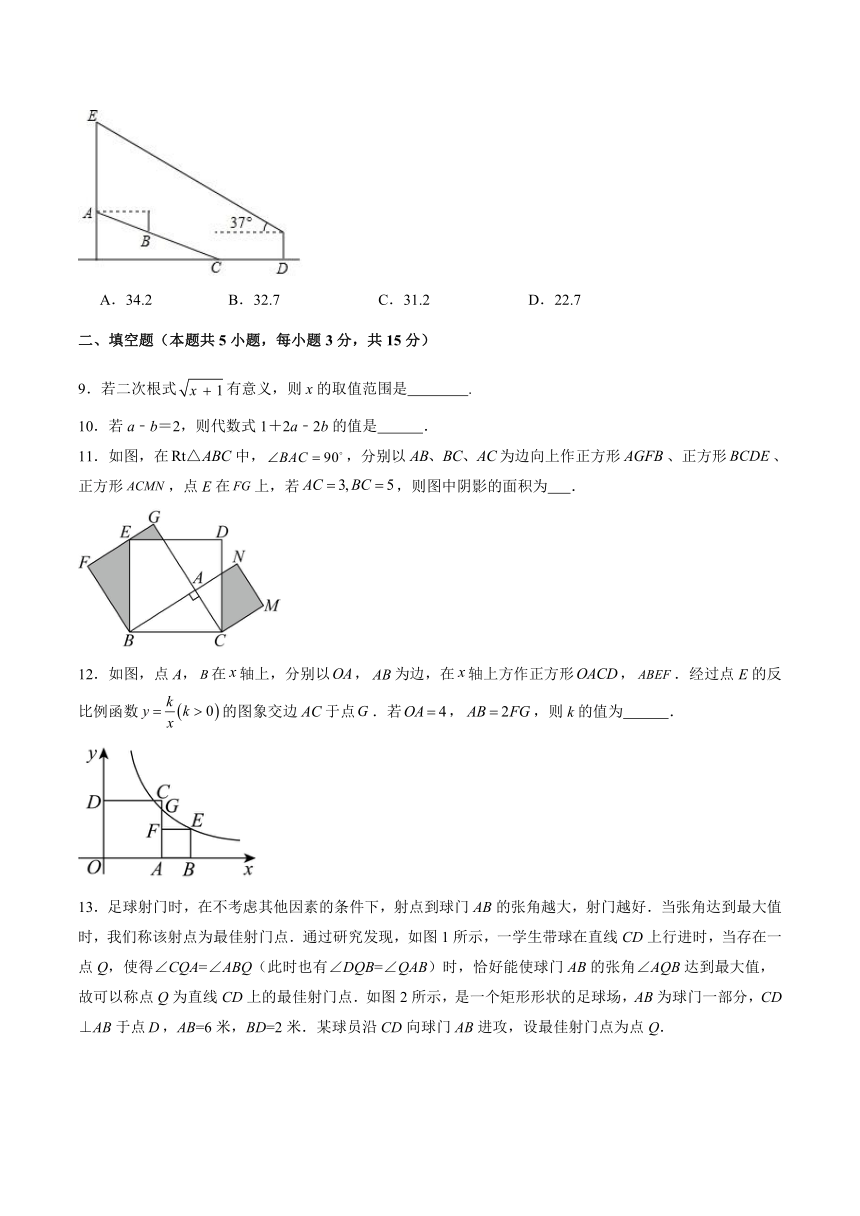
8.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.34.2 B.32.7 C.31.2 D.22.7
二、填空题(本题共5小题,每小题3分,共15分)
9.若二次根式有意义,则x的取值范围是 .
10.若a﹣b=2,则代数式1+2a﹣2b的值是 .
11.如图,在中,,分别以为边向上作正方形、正方形、正方形,点E在上,若,则图中阴影的面积为 .
12.如图,点A,在轴上,分别以,为边,在轴上方作正方形,.经过点E的反比例函数的图象交边于点.若,,则k的值为 .
13.足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好.当张角达到最大值时,我们称该射点为最佳射门点.通过研究发现,如图1所示,一学生带球在直线CD上行进时,当存在一点Q,使得∠CQA=∠ABQ(此时也有∠DQB=∠QAB)时,恰好能使球门AB的张角∠AQB达到最大值,故可以称点Q为直线CD上的最佳射门点.如图2所示,是一个矩形形状的足球场,AB为球门一部分,CD⊥AB于点,AB=6米,BD=2米.某球员沿CD向球门AB进攻,设最佳射门点为点Q.
(1)tan∠AQB = .
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.计算:.
15.先化简,再求值:,其中.
16.“绿水青山就是金山银山”,人们对生态环境的保护意识不断提高.某园区开展植树护林活动,据了解A种树木的单价比B种树木的单价多8元,且用400元购买A种树木的数量与用240元购买B种树木的数量相同.
(1)求A、B两种树木的单价;
(2)若该园区计划购买A,B两种树木共100棵,总费用不超过1600元,最多需要购买A种树木多少棵?
17.第四届全民阅读大会于2025年4月23日在山西太原开幕.大会的主题是“培育读书风尚 建设文化强国”.某校借此机会举办了主题为“书香校园 重读经典”的演讲比赛,满分为10分,得分均为整数,成绩达到6分及以上为合格,达到9分及以上为优秀.从九年级一班和九年级二班各随机抽取10名同学的成绩,并进行整理.
数据整理:小晋将随机抽取的两个班级的成绩整理成如下统计图:
数据分析:小晋对两个班级的成绩进行了如下分析:
班级 平均数/分 中位数/分 众数/分 合格率 优秀率
九年级一班
九年级二班
根据上述信息回答下列问题:
(1)填空:______,______,______.
(2)在所抽取同学的成绩中,每班成绩前的同学可以得到“阅读小能手”的称号.被抽到的小张同学的成绩是7分,他没有得到“阅读小能手”的称号.请你判断小张是哪个班级的同学,并说明理由.
(3)请你结合表格中的信息,对两个班级的成绩进行评价.(写出两条即可)
18.如图,为的内接三角形,为的直径,将沿直线翻折到,点在上.连接,交于点,延长,,两线相交于点,过点作的切线交于点.
(1)求证:;
(2)求证:;
(3)若,.求的值.
19.综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
20.综合与探究
问题情境:如图,在纸片中,,点D在边上,.沿过点D的直线折叠该纸片,使的对应线段与平行,且折痕与边交于点E,得到,然后展平.
猜想证明:(1)判断四边的形状,并说明理由;
拓展延伸:(2)如图,继续沿过点D的直线折叠该纸片,使点A的对应点落在射线上,且折痕与边交于点F,然后展平.连接交边于点G,连接.
①若,判断与的位置关系,并说明理由;
②若,,,当是以为腰的等腰三角形时,请直接写出的长.
参考答案
1.D
2.C
3.B
4.B
5.C
6.A
7.D
8.D
9.
10.5
11.12
12.12
13.
14.解:原式
.
15.解:
=
=
=,
当时,
.
16.(1)解:设每棵B种树木的单价是元,每棵A种树木的单价元
∵ 用元购买A种树木的数量与用元购买B种树木的数量相同,数量总价单价
∴
解得
经检验:是原方程的解,
∴
答:每棵A种树木的售价是20元,每棵B种树木的售价是12元.
(2)解:设需要购买A种树木棵,则购买B种树木棵
∵ 总费用不超过元,总费用A种树木费用B种树木费用,A种树木单价元,B种树木单价元
∴
解得
答:最多需要购买A种树木50棵.
17.(1)解:根据条形统计图可得,九年级一班得分中分的最多,则,
九年级二班得分分别为:则中位数为,
;
(2)小张是九年级二班的同学,理由如下:
九年级一班成绩的中位数是分,九年级二班成绩的中位数是分,小张的成绩是分
∵,且小张同学没有得到“阅读小能手”称号,
∴小张是力年级二班的同学;
(3)答案不唯一,例如∶
①九年级一班成绩的优秀率为,高于九年级二班成绩的优秀率,所以从优秀率角度看,九年级一班的成绩比九年级二班的成绩好;
②九年级一班成绩的合格率为,高于九年级二班成绩的合格率,所以从合格
率角度看,九年级一班的成绩比九年级二班的成绩好;
③九年级二班成绩的平均数为分,高于九年级一班成绩的平均数分,所以从平均数角度看,九年级二班的成绩比九年级一班的成绩好;
18.(1)证明:∵将沿直线翻折到,∴,
∵为的直径,是切线,∴,∴;
(2)解:∵是切线,∴,
∵为的直径,∴,∴,
∵由折叠可得,∴,
∵四边形是的内接四边形,
∴,
∴,
又∵,∴,∴,即;
(3)解:∵,设,则,
∴,∴,
∵由折叠可得,∴,
∵在中,,∴,
∵,,∴,
∴.
19.解:(1)∵四边形是矩形,四边形是平行四边形,,,,在边所在直线上,∴,,,
又∵如图2,在上,,,∴,
,,
当时,如图,设交于点,交于点,则,
此时遮阳区的面积为的面积,
∵,∴,,
∴,∴,
∴,
∴当时,随的增大而增大,的值从增大到;
当时,如图,设交于点,则,,,
此时遮阳区的面积为四边形的面积,
∵,∴四边形为梯形,
∴,
∴当时,随的增大而增大,的值从增大到;
综上所述,从初始起右移至图3情形的过程中,随的增大而增大;
(2)如图3,此时点落在上,则,
由(1)知:当时,;
∴图3情形时,,;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,
∴,,,
∴,,
∴,,
∴,,
∴
,
∴从图3情形起右移至与重合,该过程中关于的解析式为;
(4)当时,,
当时,的最大值为;当时,,
当时,的最大值为;
当时,,
∵,∴当时,的最大值为,
综上所述,当时,取得最大值,最大值为,
∴当遮阳区面积最大时,向右移动了.
20.(1)解:四边形是菱形,理由如下:
由折叠的性质可得,,
∵,∴,∴,
∴,∴,
∴四边形是菱形;
(2)①,理由如下:
由(1)知四边形是菱形,∴,
由折叠的性质得到,
∵,∴,
∴,∴,
∵,∴,∴;
②∵,,,
∴,
当是以为腰为底的等腰三角形时,如图,延长交于点H,设交点为,则,
∵,,∴,∴,
由折叠的性质得,,,
∴,∴;
∵,∴;
∵,∴,∴,
∴,
∵,
∴,∴,
设,
∴,
∵,∴,
∴,即,∴,
∴,∴,
∵,∴,
∴,
∵,∴,∴,
∴,解得,∴;
当是以为腰为底的等腰三角形时,如图,则,
同理得,,
设,
∴,
∵,∴,
∴,即,∴,
∴,∴,
∵是以为腰为底的等腰三角形,,
∴,∴,∴,
∵,∴,∴,
∴,解得,∴;
综上,的长为或.
说明:本卷共6页,考试时间90分钟,满分100分,题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码.考试结束后,请将本卷和题卡一并上交.
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.位于贵州的“中国天眼”是500米口径球面射电望远镜,简称,是世界上最大的单口径球面射电望远镜(如图所示),它的俯视图是( )
A. B.C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°
4.如图,点P是的重心.过P作的平行线,分别交,于点D,E;作交于点F.若的面积为18,则四边形的面积为( )
A.6 B.8 C.10 D.12
5.化学实验室有四种溶液:分别是氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,从中随机取出两种适量溶液,充分混合,有气体生成的概率是( )
A. B. C. D.
6.我国古代数学名著《张丘建算经》中记载:“今有甲、乙怀钱,各不知其数,甲得乙十钱多乙余钱五倍,乙得甲十钱适等,问甲、乙怀钱各几何 ”译文为:现有甲、乙两人带有一些银子,都不知道数量,甲得到乙的10两银子,甲比乙多出的银子是乙的5倍,乙得到甲的10两银子,两人的银子恰好相等,问甲、乙各带了多少两银子 设甲带了两银子,乙带了两银子,那么可列方程组为( )
A. B.
C. D.
7.如图,四边形与四边形都是菱形,点E,F在上,已知,,则的值为( )
A. B. C. D.
8.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.34.2 B.32.7 C.31.2 D.22.7
二、填空题(本题共5小题,每小题3分,共15分)
9.若二次根式有意义,则x的取值范围是 .
10.若a﹣b=2,则代数式1+2a﹣2b的值是 .
11.如图,在中,,分别以为边向上作正方形、正方形、正方形,点E在上,若,则图中阴影的面积为 .
12.如图,点A,在轴上,分别以,为边,在轴上方作正方形,.经过点E的反比例函数的图象交边于点.若,,则k的值为 .
13.足球射门时,在不考虑其他因素的条件下,射点到球门AB的张角越大,射门越好.当张角达到最大值时,我们称该射点为最佳射门点.通过研究发现,如图1所示,一学生带球在直线CD上行进时,当存在一点Q,使得∠CQA=∠ABQ(此时也有∠DQB=∠QAB)时,恰好能使球门AB的张角∠AQB达到最大值,故可以称点Q为直线CD上的最佳射门点.如图2所示,是一个矩形形状的足球场,AB为球门一部分,CD⊥AB于点,AB=6米,BD=2米.某球员沿CD向球门AB进攻,设最佳射门点为点Q.
(1)tan∠AQB = .
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.计算:.
15.先化简,再求值:,其中.
16.“绿水青山就是金山银山”,人们对生态环境的保护意识不断提高.某园区开展植树护林活动,据了解A种树木的单价比B种树木的单价多8元,且用400元购买A种树木的数量与用240元购买B种树木的数量相同.
(1)求A、B两种树木的单价;
(2)若该园区计划购买A,B两种树木共100棵,总费用不超过1600元,最多需要购买A种树木多少棵?
17.第四届全民阅读大会于2025年4月23日在山西太原开幕.大会的主题是“培育读书风尚 建设文化强国”.某校借此机会举办了主题为“书香校园 重读经典”的演讲比赛,满分为10分,得分均为整数,成绩达到6分及以上为合格,达到9分及以上为优秀.从九年级一班和九年级二班各随机抽取10名同学的成绩,并进行整理.
数据整理:小晋将随机抽取的两个班级的成绩整理成如下统计图:
数据分析:小晋对两个班级的成绩进行了如下分析:
班级 平均数/分 中位数/分 众数/分 合格率 优秀率
九年级一班
九年级二班
根据上述信息回答下列问题:
(1)填空:______,______,______.
(2)在所抽取同学的成绩中,每班成绩前的同学可以得到“阅读小能手”的称号.被抽到的小张同学的成绩是7分,他没有得到“阅读小能手”的称号.请你判断小张是哪个班级的同学,并说明理由.
(3)请你结合表格中的信息,对两个班级的成绩进行评价.(写出两条即可)
18.如图,为的内接三角形,为的直径,将沿直线翻折到,点在上.连接,交于点,延长,,两线相交于点,过点作的切线交于点.
(1)求证:;
(2)求证:;
(3)若,.求的值.
19.综合与实践
树人中学组织一次“爱心义卖”活动.九(5)班分配到了一块矩形义卖区和一把遮阳伞,遮阳伞在地面上的投影是一个平行四边形(如图1)
初始时,矩形义卖区与遮阳伞投影的平面图如图2所示,在上,,,,,,由于场地限制,参加义卖的同学只能左右平移遮阳伞.在移动过程中,也随之移动(始终在边所在直线上),且形状大小保持不变,但落在义卖区内的部分(遮阳区)会呈现不同的形状.如图3为移动到落在上的情形.
【问题提出】
西西同学打算用数学方法,确定遮阳区面积最大时的位置.
设遮阳区的面积为,从初始时向右移动的距离为.
【直观感知】(1)从初始起右移至图3情形的过程中,随的增大如何变化?
【初步探究】(2)求图3情形的与的值;
【深入研究】(3)从图3情形起右移至与重合,求该过程中关于的解析式;
【问题解决】(4)当遮阳区面积最大时,向右移动了多少?(直接写出结果)
20.综合与探究
问题情境:如图,在纸片中,,点D在边上,.沿过点D的直线折叠该纸片,使的对应线段与平行,且折痕与边交于点E,得到,然后展平.
猜想证明:(1)判断四边的形状,并说明理由;
拓展延伸:(2)如图,继续沿过点D的直线折叠该纸片,使点A的对应点落在射线上,且折痕与边交于点F,然后展平.连接交边于点G,连接.
①若,判断与的位置关系,并说明理由;
②若,,,当是以为腰的等腰三角形时,请直接写出的长.
参考答案
1.D
2.C
3.B
4.B
5.C
6.A
7.D
8.D
9.
10.5
11.12
12.12
13.
14.解:原式
.
15.解:
=
=
=,
当时,
.
16.(1)解:设每棵B种树木的单价是元,每棵A种树木的单价元
∵ 用元购买A种树木的数量与用元购买B种树木的数量相同,数量总价单价
∴
解得
经检验:是原方程的解,
∴
答:每棵A种树木的售价是20元,每棵B种树木的售价是12元.
(2)解:设需要购买A种树木棵,则购买B种树木棵
∵ 总费用不超过元,总费用A种树木费用B种树木费用,A种树木单价元,B种树木单价元
∴
解得
答:最多需要购买A种树木50棵.
17.(1)解:根据条形统计图可得,九年级一班得分中分的最多,则,
九年级二班得分分别为:则中位数为,
;
(2)小张是九年级二班的同学,理由如下:
九年级一班成绩的中位数是分,九年级二班成绩的中位数是分,小张的成绩是分
∵,且小张同学没有得到“阅读小能手”称号,
∴小张是力年级二班的同学;
(3)答案不唯一,例如∶
①九年级一班成绩的优秀率为,高于九年级二班成绩的优秀率,所以从优秀率角度看,九年级一班的成绩比九年级二班的成绩好;
②九年级一班成绩的合格率为,高于九年级二班成绩的合格率,所以从合格
率角度看,九年级一班的成绩比九年级二班的成绩好;
③九年级二班成绩的平均数为分,高于九年级一班成绩的平均数分,所以从平均数角度看,九年级二班的成绩比九年级一班的成绩好;
18.(1)证明:∵将沿直线翻折到,∴,
∵为的直径,是切线,∴,∴;
(2)解:∵是切线,∴,
∵为的直径,∴,∴,
∵由折叠可得,∴,
∵四边形是的内接四边形,
∴,
∴,
又∵,∴,∴,即;
(3)解:∵,设,则,
∴,∴,
∵由折叠可得,∴,
∵在中,,∴,
∵,,∴,
∴.
19.解:(1)∵四边形是矩形,四边形是平行四边形,,,,在边所在直线上,∴,,,
又∵如图2,在上,,,∴,
,,
当时,如图,设交于点,交于点,则,
此时遮阳区的面积为的面积,
∵,∴,,
∴,∴,
∴,
∴当时,随的增大而增大,的值从增大到;
当时,如图,设交于点,则,,,
此时遮阳区的面积为四边形的面积,
∵,∴四边形为梯形,
∴,
∴当时,随的增大而增大,的值从增大到;
综上所述,从初始起右移至图3情形的过程中,随的增大而增大;
(2)如图3,此时点落在上,则,
由(1)知:当时,;
∴图3情形时,,;
(3)当时,如图,设向右移动后得到,设交于点,交于点,交于点,则,,
此时遮阳区的面积为六边形的面积,
∴,,,
∴,,
∴,,
∴,,
∴
,
∴从图3情形起右移至与重合,该过程中关于的解析式为;
(4)当时,,
当时,的最大值为;当时,,
当时,的最大值为;
当时,,
∵,∴当时,的最大值为,
综上所述,当时,取得最大值,最大值为,
∴当遮阳区面积最大时,向右移动了.
20.(1)解:四边形是菱形,理由如下:
由折叠的性质可得,,
∵,∴,∴,
∴,∴,
∴四边形是菱形;
(2)①,理由如下:
由(1)知四边形是菱形,∴,
由折叠的性质得到,
∵,∴,
∴,∴,
∵,∴,∴;
②∵,,,
∴,
当是以为腰为底的等腰三角形时,如图,延长交于点H,设交点为,则,
∵,,∴,∴,
由折叠的性质得,,,
∴,∴;
∵,∴;
∵,∴,∴,
∴,
∵,
∴,∴,
设,
∴,
∵,∴,
∴,即,∴,
∴,∴,
∵,∴,
∴,
∵,∴,∴,
∴,解得,∴;
当是以为腰为底的等腰三角形时,如图,则,
同理得,,
设,
∴,
∵,∴,
∴,即,∴,
∴,∴,
∵是以为腰为底的等腰三角形,,
∴,∴,∴,
∵,∴,∴,
∴,解得,∴;
综上,的长为或.
同课章节目录
