广东省深圳市2025年九年级下学期中考模拟数学练习卷(三)(含答案)
文档属性
| 名称 | 广东省深圳市2025年九年级下学期中考模拟数学练习卷(三)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 958.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 18:12:37 | ||
图片预览



文档简介
2025年九年级第二学期深圳中考数学练习卷(三)
说明:本卷共6页,考试时间90分钟,满分100分,题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码.考试结束后,请将本卷和题卡一并上交.
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是
正确的)
1.下列由相同的小正方体搭成的几何体中,其主视图和左视图相同的是( )
A.B.C.D.
2.下列计算正确的是( )
A. B.
C. D.
3.如图是凸透镜成像原理图,已知物和像都与主光轴垂直,,则的度数为( )
A. B. C. D.
4.若,它们对应高的比为,那么它们面积的比为( )
A. B. C. D.
5.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是()
A. B. C. D.
6.用1块A型钢板可制成3块C型钢板和4块D型钢板;用1块B型钢板可制成5块C型钢板和2块D型钢板.现在需要58块C型钢板、40块D型钢板,问恰好用A型钢板、B型钢板各多少块?如果设用A型钢板块,用B型钢板块,则可列方程组为( )
A. B.
C. D.
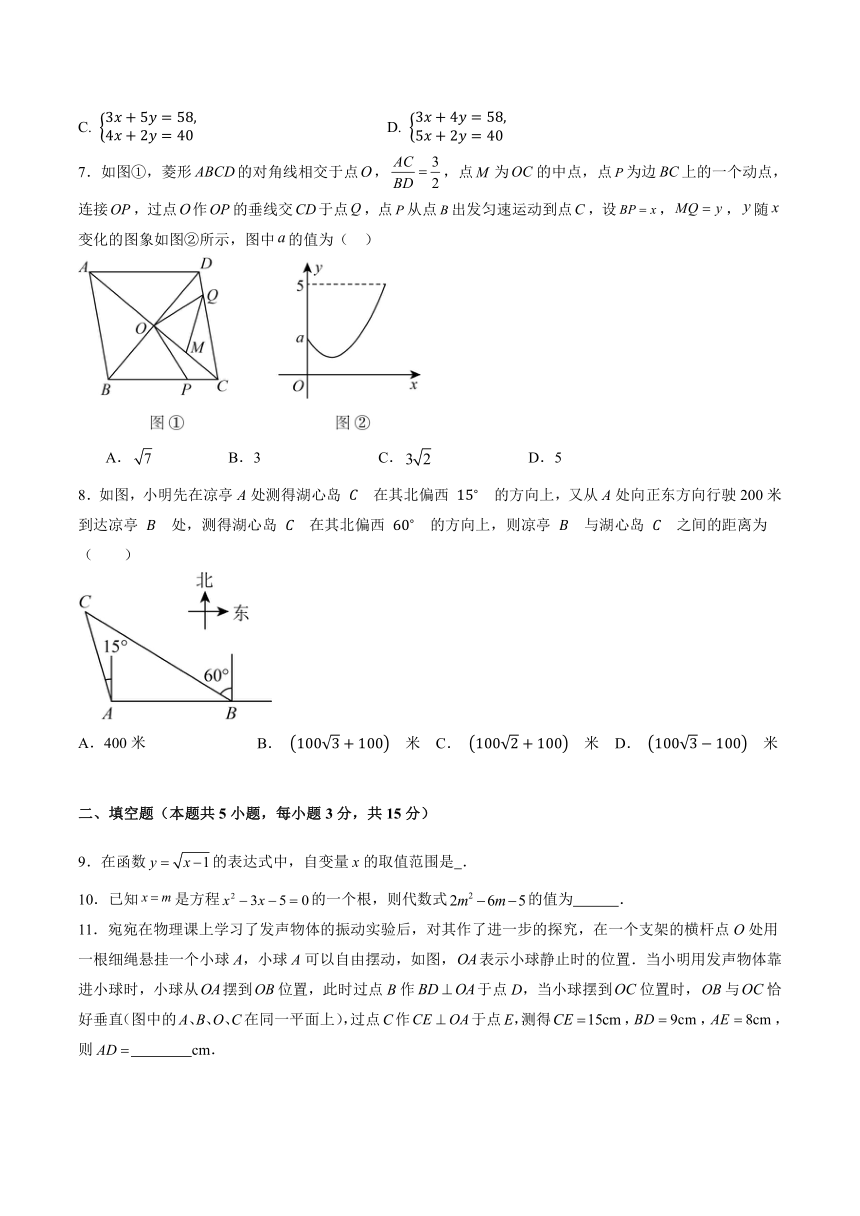
7.如图①,菱形的对角线相交于点,,点为的中点,点为边上的一个动点,连接,过点作的垂线交于点,点从点出发匀速运动到点,设,,随变化的图象如图②所示,图中的值为( )
A. B.3 C. D.5
8.如图,小明先在凉亭A处测得湖心岛 在其北偏西 的方向上,又从A处向正东方向行驶200米到达凉亭 处,测得湖心岛 在其北偏西 的方向上,则凉亭 与湖心岛 之间的距离为( )
A.400米 B. 米 C. 米 D. 米
二、填空题(本题共5小题,每小题3分,共15分)
9.在函数的表达式中,自变量x的取值范围是 .
10.已知是方程的一个根,则代数式的值为 .
11.宛宛在物理课上学习了发声物体的振动实验后,对其作了进一步的探究,在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠进小球时,小球从摆到位置,此时过点B作于点D,当小球摆到位置时,与恰好垂直(图中的A、B、O、C在同一平面上),过点C作于点E,测得,,,则 cm.
12.如图,已知反比例函数与正比例函数的图象,点,点与点均在反比例函数的图象上,点在直线上,四边形是平行四边形,则点的坐标为 .
13.如图,在矩形中,是的中点,过点E作的垂线交于点,对角线分别交,于点,,当时,则的值为 .
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.计算:.
15.先化简,再求值:,其中.
16.在2025年春晚舞台上,有扭秧歌的宇树人形机器人和.它们身着大红棉袄、扭着秧歌转着手绢,凭借流畅的舞姿和精准的互动,成为“科技顶流”.为了更好地开设智能机器人编程的校本课程,某学校打算购买A,B两种型号的机器人模型用于教学.A型机器人模型单价比B型机器人模型单价多80元,用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同.
(1)求A,B两种型号模型的单价;
(2)学校准备再次购买A型和B型机器人模型共20台,购买B型机器人模型不超过A型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠.问购买A型和B型机器人模型各多少台时花费最少?最少花费是多少元?
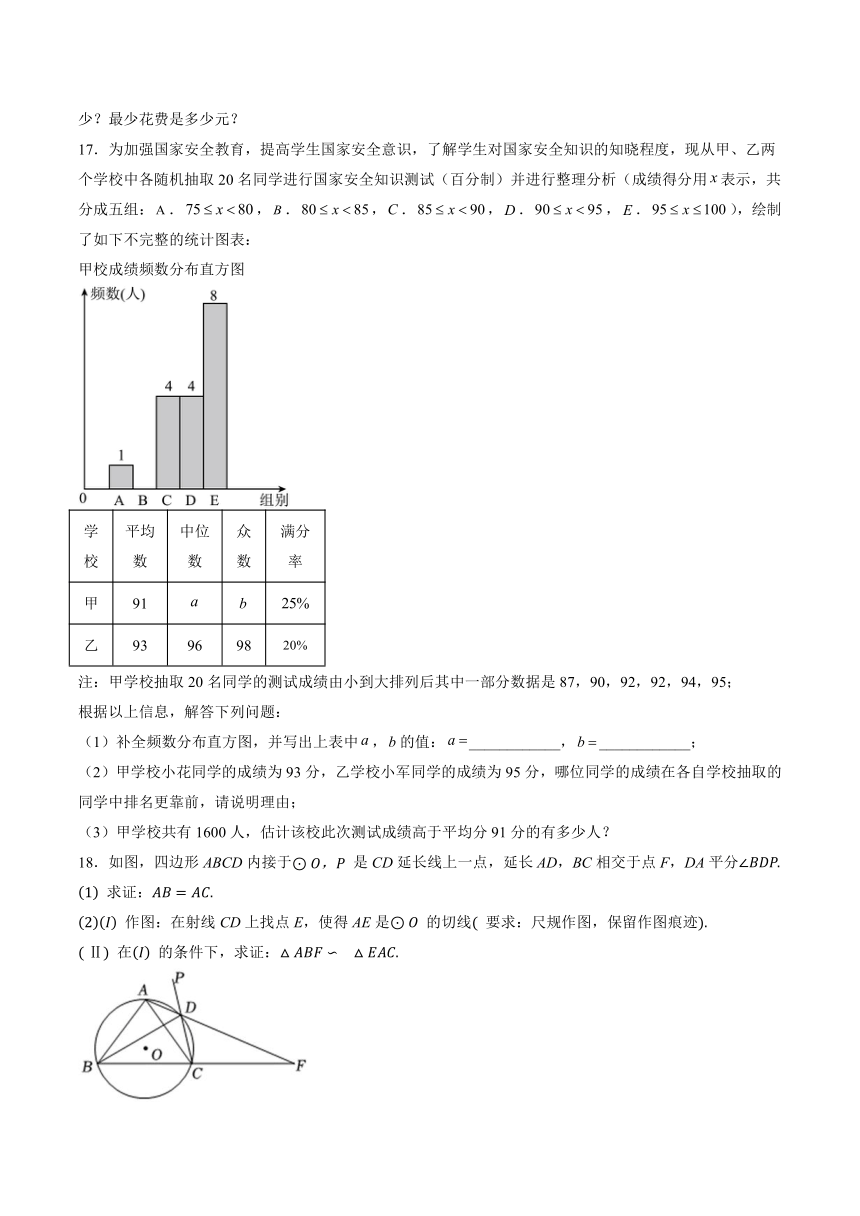
17.为加强国家安全教育,提高学生国家安全意识,了解学生对国家安全知识的知晓程度,现从甲、乙两个学校中各随机抽取20名同学进行国家安全知识测试(百分制)并进行整理分析(成绩得分用表示,共分成五组:.,.,.,.,.),绘制了如下不完整的统计图表:
甲校成绩频数分布直方图
学校 平均数 中位数 众数 满分率
甲 91
乙 93 96 98
注:甲学校抽取20名同学的测试成绩由小到大排列后其中一部分数据是87,90,92,92,94,95;
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并写出上表中,的值:____________,____________;
(2)甲学校小花同学的成绩为93分,乙学校小军同学的成绩为95分,哪位同学的成绩在各自学校抽取的同学中排名更靠前,请说明理由;
(3)甲学校共有1600人,估计该校此次测试成绩高于平均分91分的有多少人?
18.如图,四边形ABCD内接于 是CD延长线上一点,延长AD,BC相交于点F,DA平分
求证:
作图:在射线CD上找点E,使得AE是 的切线 要求:尺规作图,保留作图痕迹
Ⅱ 在 的条件下,求证:
19.问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为,在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴,建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
20.如图1,抛物线交轴于两点(点在点的左边),交轴于点.
(1)直接写出点的坐标.
(2)如图1,点为抛物线上一点,直线和直线交于点,若,求点坐标.
(3)如图2,点和分别是抛物线上两点,且点在点的左侧,点在点的右侧,直线和交于点,直线和交于点,连接,若点横坐标为,求证:的中点是定点,且在此抛物线上.
参考答案
1.D
2.D
3.D
4.B
5.A
6.C
7.B
8.B
9.
10.5
11.
12.(,)
13./
14.解:原式.
15.解:原式
16.(1)解:设B型机器人模型单价是x元,则A型机器人模型单价是元,
根据题意,得.
解得,
经检验,是原分式方程的解,
∴(元).
答:A型机器人模型单价是200元,B型机器人模型单价120元.
(2)解:设购买A型机器人模型a台,则购买B型机器人模型台,
根据题意,得,
解得,
设花费W元,
则,
,
∴W随a的减小而减小,
,
∴当时W值最小,,
∴(台),
答:购买A型机器人模型5台,B型机器人模型15台时花费最少,最少花费是2240元.
17.(1)解:甲校成绩组人数为(人),
故可补全频数分布直方图如下,
由统计表可知,甲学校抽取学生中的满分(100分)的有(人),
由统计表可知,组有8人,
结合由小到大排列后其中一部分数据是87,90,92,92,94,95,
可甲学校成绩按照从大到小的顺序排列,排在第10和11位的是92和92,
故甲校成绩的中位数;
甲学校成绩中,出现次数做多的是100,
故甲学校成绩的众数.
(2)小花同学的成绩在各自学校抽取的同学中排名更靠前,理由如下:
甲学校的中位数为92,而小花同学的成绩为93分,比其学校成绩的中位数大,
乙学校的中位数为96,而小军同学的成绩为95分,比其学校成绩的中位数小,
故小花同学的成绩在各自学校抽取的同学中排名更靠前;
(3)由图表可知,甲学校所抽取的学生成绩在91分以上的有11人,
(人),
所以,估计该校此次测试成绩高于平均分91分的有880人.
18. 证明: 平分 ,
,
四边形ABCD为圆的内接四边形,
,
,
,
;
Ⅰ 如图所示,点E即为所求;
Ⅱ 证明:连接AO并延长交BC于点G,如图,
由 知: ,
, ,
,
是 的切线,
,
,
, ,
是 的切线,
,
,
19.(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,解得,
则抛物线的表达式为;
将代入,解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,解得或(在对称轴右侧,舍),
∴,由抛物线对称性可得.
20.(1)解:把代入得,
解得:,,
∴,;
把代入得,
∴;
(2)解:当D点在第一象限时,将绕着A点顺时针旋转,得到,
∴为等腰直角三角形.
∴,
∴,
∵,
∴.
∵,
∴.
∴,
∵,,
∴.
∴,.
∴,设直线的解析式为,
代入H点坐标,得到:,
解得:,
∵BG//HC,
∴设直线的解析式为.
代入,可得:,
解得.
∴直线的解析式为,
联立抛物线,可得:,
解得:(舍).
∴D点坐标为.
过点B作,交于点,交抛物线于点,如图所示:
则,
∵,
∴,
∴此时点也符合题意,
过点D作轴于点E,
则,,,
∴,
∵,
∴,
∴,
∴,
即,
∴,
∴,
设直线的解析式为:,
把代入得:,
解得:,
∴直线的解析式为:,
令,
解得:,,
把代入得,
∴点坐标为;
综上分析可知点D的坐标为或.
(3)解:设直线的解析式为,直线的解析式为,
联立抛物线,可得:,
解得:,
同理:.
设直线的解析式为,设直线的解析式为,
联立抛物线,可得:,
解得:.
同理:.
因此,,.
整理得:,,
联立直线和,可得:,
解得:.
∵.
∴,
代入,,
∴,
∴.
同理,联立直线和,可得:,
∴,
∵,,
∴P点坐标为,Q点坐标为.
∵M是的中点,根据中点坐标公式可得:
M点横坐标是,
M点纵坐标是.
∵,
∴.
即:点M为定点,
且满足,
∴点M在抛物线上.
说明:本卷共6页,考试时间90分钟,满分100分,题前,请将姓名、考号、考点、考场和座位号填写在答题卡相应的区域,并贴好条形码.考试结束后,请将本卷和题卡一并上交.
一、选择题(本大题共8小题,每小题3分,共24分,每小题有四个选项,其中只有一个是
正确的)
1.下列由相同的小正方体搭成的几何体中,其主视图和左视图相同的是( )
A.B.C.D.
2.下列计算正确的是( )
A. B.
C. D.
3.如图是凸透镜成像原理图,已知物和像都与主光轴垂直,,则的度数为( )
A. B. C. D.
4.若,它们对应高的比为,那么它们面积的比为( )
A. B. C. D.
5.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是()
A. B. C. D.
6.用1块A型钢板可制成3块C型钢板和4块D型钢板;用1块B型钢板可制成5块C型钢板和2块D型钢板.现在需要58块C型钢板、40块D型钢板,问恰好用A型钢板、B型钢板各多少块?如果设用A型钢板块,用B型钢板块,则可列方程组为( )
A. B.
C. D.
7.如图①,菱形的对角线相交于点,,点为的中点,点为边上的一个动点,连接,过点作的垂线交于点,点从点出发匀速运动到点,设,,随变化的图象如图②所示,图中的值为( )
A. B.3 C. D.5
8.如图,小明先在凉亭A处测得湖心岛 在其北偏西 的方向上,又从A处向正东方向行驶200米到达凉亭 处,测得湖心岛 在其北偏西 的方向上,则凉亭 与湖心岛 之间的距离为( )
A.400米 B. 米 C. 米 D. 米
二、填空题(本题共5小题,每小题3分,共15分)
9.在函数的表达式中,自变量x的取值范围是 .
10.已知是方程的一个根,则代数式的值为 .
11.宛宛在物理课上学习了发声物体的振动实验后,对其作了进一步的探究,在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,表示小球静止时的位置.当小明用发声物体靠进小球时,小球从摆到位置,此时过点B作于点D,当小球摆到位置时,与恰好垂直(图中的A、B、O、C在同一平面上),过点C作于点E,测得,,,则 cm.
12.如图,已知反比例函数与正比例函数的图象,点,点与点均在反比例函数的图象上,点在直线上,四边形是平行四边形,则点的坐标为 .
13.如图,在矩形中,是的中点,过点E作的垂线交于点,对角线分别交,于点,,当时,则的值为 .
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.计算:.
15.先化简,再求值:,其中.
16.在2025年春晚舞台上,有扭秧歌的宇树人形机器人和.它们身着大红棉袄、扭着秧歌转着手绢,凭借流畅的舞姿和精准的互动,成为“科技顶流”.为了更好地开设智能机器人编程的校本课程,某学校打算购买A,B两种型号的机器人模型用于教学.A型机器人模型单价比B型机器人模型单价多80元,用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同.
(1)求A,B两种型号模型的单价;
(2)学校准备再次购买A型和B型机器人模型共20台,购买B型机器人模型不超过A型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠.问购买A型和B型机器人模型各多少台时花费最少?最少花费是多少元?
17.为加强国家安全教育,提高学生国家安全意识,了解学生对国家安全知识的知晓程度,现从甲、乙两个学校中各随机抽取20名同学进行国家安全知识测试(百分制)并进行整理分析(成绩得分用表示,共分成五组:.,.,.,.,.),绘制了如下不完整的统计图表:
甲校成绩频数分布直方图
学校 平均数 中位数 众数 满分率
甲 91
乙 93 96 98
注:甲学校抽取20名同学的测试成绩由小到大排列后其中一部分数据是87,90,92,92,94,95;
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并写出上表中,的值:____________,____________;
(2)甲学校小花同学的成绩为93分,乙学校小军同学的成绩为95分,哪位同学的成绩在各自学校抽取的同学中排名更靠前,请说明理由;
(3)甲学校共有1600人,估计该校此次测试成绩高于平均分91分的有多少人?
18.如图,四边形ABCD内接于 是CD延长线上一点,延长AD,BC相交于点F,DA平分
求证:
作图:在射线CD上找点E,使得AE是 的切线 要求:尺规作图,保留作图痕迹
Ⅱ 在 的条件下,求证:
19.问题背景:
综合与实践课上,老师让同学们设计一个家电装置图案,某小组设计的效果图如图所示.
外形参数:
如图1,装置整体图案为轴对称图形,外形由上方的抛物线,中间的矩形和下方的抛物线组成.抛物线的高度为,矩形的边,,抛物线的高度为,在装置内部安装矩形电子显示屏,点,在抛物线上,点,在抛物线上.
问题解决:
如图2,该小组以矩形的顶点为原点,以边所在的直线为轴,以边所在的直线为轴,建立平面直角坐标系.请结合外形参数,完成以下任务:
(1)直接写出,,三点的坐标;
(2)直接写出抛物线和的顶点坐标,并分别求出抛物线和的函数表达式;
(3)为满足矩形电子显示屏的空间要求,需要边的长为,求此时边的长.
20.如图1,抛物线交轴于两点(点在点的左边),交轴于点.
(1)直接写出点的坐标.
(2)如图1,点为抛物线上一点,直线和直线交于点,若,求点坐标.
(3)如图2,点和分别是抛物线上两点,且点在点的左侧,点在点的右侧,直线和交于点,直线和交于点,连接,若点横坐标为,求证:的中点是定点,且在此抛物线上.
参考答案
1.D
2.D
3.D
4.B
5.A
6.C
7.B
8.B
9.
10.5
11.
12.(,)
13./
14.解:原式.
15.解:原式
16.(1)解:设B型机器人模型单价是x元,则A型机器人模型单价是元,
根据题意,得.
解得,
经检验,是原分式方程的解,
∴(元).
答:A型机器人模型单价是200元,B型机器人模型单价120元.
(2)解:设购买A型机器人模型a台,则购买B型机器人模型台,
根据题意,得,
解得,
设花费W元,
则,
,
∴W随a的减小而减小,
,
∴当时W值最小,,
∴(台),
答:购买A型机器人模型5台,B型机器人模型15台时花费最少,最少花费是2240元.
17.(1)解:甲校成绩组人数为(人),
故可补全频数分布直方图如下,
由统计表可知,甲学校抽取学生中的满分(100分)的有(人),
由统计表可知,组有8人,
结合由小到大排列后其中一部分数据是87,90,92,92,94,95,
可甲学校成绩按照从大到小的顺序排列,排在第10和11位的是92和92,
故甲校成绩的中位数;
甲学校成绩中,出现次数做多的是100,
故甲学校成绩的众数.
(2)小花同学的成绩在各自学校抽取的同学中排名更靠前,理由如下:
甲学校的中位数为92,而小花同学的成绩为93分,比其学校成绩的中位数大,
乙学校的中位数为96,而小军同学的成绩为95分,比其学校成绩的中位数小,
故小花同学的成绩在各自学校抽取的同学中排名更靠前;
(3)由图表可知,甲学校所抽取的学生成绩在91分以上的有11人,
(人),
所以,估计该校此次测试成绩高于平均分91分的有880人.
18. 证明: 平分 ,
,
四边形ABCD为圆的内接四边形,
,
,
,
;
Ⅰ 如图所示,点E即为所求;
Ⅱ 证明:连接AO并延长交BC于点G,如图,
由 知: ,
, ,
,
是 的切线,
,
,
, ,
是 的切线,
,
,
19.(1)解:∵矩形的边,,
∴,,,,
∴,,;
(2)解:∵装置整体图案为轴对称图形,
如图,作出对称轴,分别交抛物线于,交抛物线于,交矩形于,,
结合矩形和抛物线的对称性,可得直线是抛物线和的对称轴,,,
∴四边形是矩形,
∴,
∵抛物线的高度为,抛物线的高度为,直线是抛物线和的对称轴,
∴,,
∴抛物线和的顶点坐标分别为,,
分别设抛物线和的表达式为,,
将代入,解得,
则抛物线的表达式为;
将代入,解得;
则抛物线的表达式为;
(3)解:∵装置整体图案为轴对称图形,
∴,,
∵轴,∴轴,
∵是矩形,
∴,
∴轴,
∴,
设,
∴,,
∴,解得或(在对称轴右侧,舍),
∴,由抛物线对称性可得.
20.(1)解:把代入得,
解得:,,
∴,;
把代入得,
∴;
(2)解:当D点在第一象限时,将绕着A点顺时针旋转,得到,
∴为等腰直角三角形.
∴,
∴,
∵,
∴.
∵,
∴.
∴,
∵,,
∴.
∴,.
∴,设直线的解析式为,
代入H点坐标,得到:,
解得:,
∵BG//HC,
∴设直线的解析式为.
代入,可得:,
解得.
∴直线的解析式为,
联立抛物线,可得:,
解得:(舍).
∴D点坐标为.
过点B作,交于点,交抛物线于点,如图所示:
则,
∵,
∴,
∴此时点也符合题意,
过点D作轴于点E,
则,,,
∴,
∵,
∴,
∴,
∴,
即,
∴,
∴,
设直线的解析式为:,
把代入得:,
解得:,
∴直线的解析式为:,
令,
解得:,,
把代入得,
∴点坐标为;
综上分析可知点D的坐标为或.
(3)解:设直线的解析式为,直线的解析式为,
联立抛物线,可得:,
解得:,
同理:.
设直线的解析式为,设直线的解析式为,
联立抛物线,可得:,
解得:.
同理:.
因此,,.
整理得:,,
联立直线和,可得:,
解得:.
∵.
∴,
代入,,
∴,
∴.
同理,联立直线和,可得:,
∴,
∵,,
∴P点坐标为,Q点坐标为.
∵M是的中点,根据中点坐标公式可得:
M点横坐标是,
M点纵坐标是.
∵,
∴.
即:点M为定点,
且满足,
∴点M在抛物线上.
同课章节目录
