人教A版(2019)必修第二册 8.1.2 样本相关系数 课件(共19张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册 8.1.2 样本相关系数 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览



文档简介
课前准备:
课本、笔记本、草稿纸、笔
天道酬勤,勤能补拙!
8.1.2样本相关系数
形
数
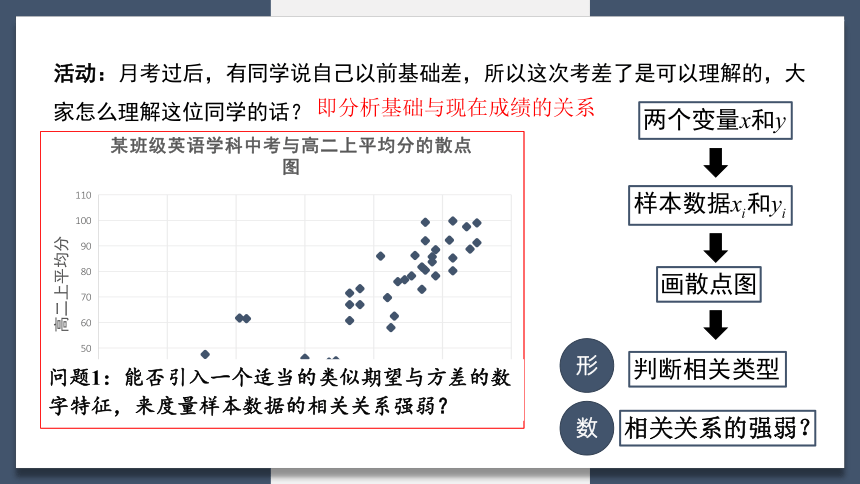
活动:月考过后,有同学说自己以前基础差,所以这次考差了是可以理解的,大家怎么理解这位同学的话?
问题1:能否引入一个适当的类似期望与方差的数字特征,来度量样本数据的相关关系强弱?
即分析基础与现在成绩的关系
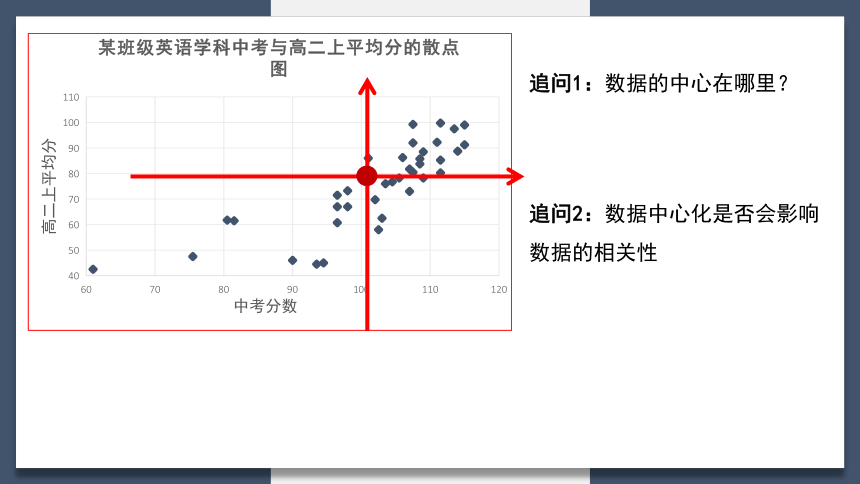
追问1:数据的中心在哪里?
追问2:数据中心化是否会影响数据的相关性
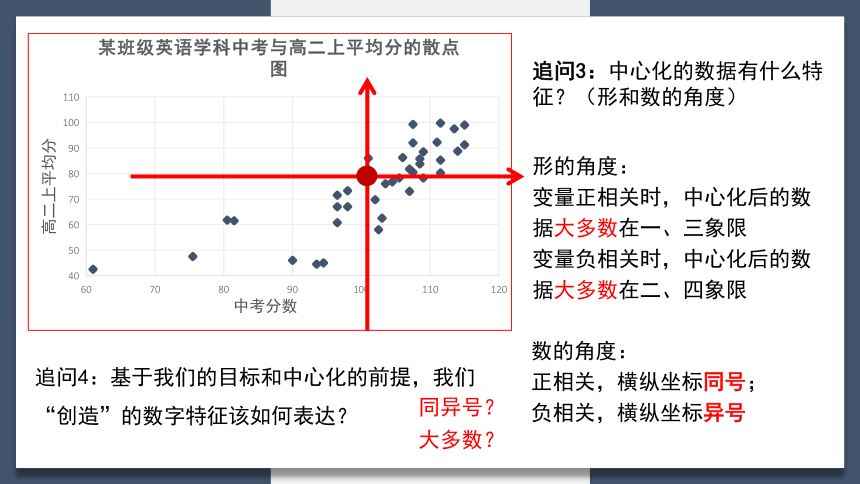
追问3:中心化的数据有什么特征?(形和数的角度)
追问4:基于我们的目标和中心化的前提,我们“创造”的数字特征该如何表达?
形的角度:
变量正相关时,中心化后的数据大多数在一、三象限
变量负相关时,中心化后的数据大多数在二、四象限
数的角度:
正相关,横纵坐标同号;
负相关,横纵坐标异号
大多数?
同异号?
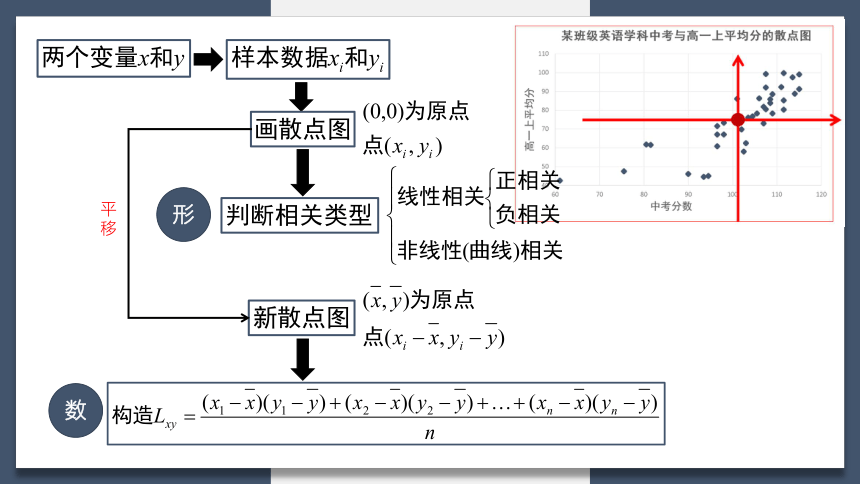
累加
“同异号”
“大多数”
平移
形
数
问题2:从计算角度思考式子中存在的局限性
容易受样本数据的度量单位影响!
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,
则相应的????????????将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
?
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
称r为变量x和变量y的样本相关系数(Sample Correlation coefficient)
“标准化”
形
数
Bug:Lxy的大小受数据的度量单位的影响,但单位的改变并不会导致两个变量之间相关程度的改变.
r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本相关系数:
问题3:r的取值范围是什么?
强
强
弱
弱
思考:若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-2x+1上,问这组样本数据的样本相关系数?
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,
故|r|越接近1时,线性相关程度越强;
|r|越接近0时,线性相关程度越弱;
思考:若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-2x+1上,问这组样本数据的样本相关系数?
卡尔·皮尔逊,是英国数学家,生物统计学家,数理统计学的创立者,自由思想者,对生物统计学、气象学、社会达尔文主义理论和优生学做出了重大贡献。他被公认是旧派理学派和描述统计学派的代表人物,并被誉为现代统计科学的创立者。是20世纪科学革命和哲学革命的先驱,“批判学派”代表人物之一。
“统计是科学的语法”
追问:r=0是否反映成对数据没有关系?
活动:月考过后,有听到同学说自己以前基础差,所以这次考差了是可以理解的,大家认同这句话吗?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}各科不同阶段与中考成绩的样本相关系数
高一上
高二上
语文
0.56
0.71
数学
0.66
0.46
英语
0.81
0.47
活动:月考过后,有听到同学说自己以前基础差,所以这次考差了是可以理解的,大家认同这句话吗?
1.学科上来看,初中的英语对高中学习有较大影响,即初中英语好的同学,大概率高中入学英语也不错。
2.从不同年段角度分析,数学与英语学科随着高中学习时间的增加,高中成绩的好坏与初中基础的相关程度降低。
天道酬勤,勤能补拙
=
作业:
1.完成分层作业
2.思考本节课你感到最难的内容是什么?我们是怎么突破的?
3.尝试证明下式:
4.周末尝试借助EXCEL分析其他学科的成绩数据,并总结收获
思考:本节课你感到最难的内容是什么?我们是怎么突破的?
=
作业:
1.完成分层作业
2.尝试证明下式:
3.周末尝试借助EXCEL分析其他学科的成绩数据,并总结收获
回顾:期望与方差的反映了数据怎样的数字特征
均值反映了随机变量取值的平均水平.
即反映随机变量变量分布的中心趋势
方差与标准差反映随机变量取值的离散程度
注:方差与标准差的单位不同,后者与数据单位一致
课本、笔记本、草稿纸、笔
天道酬勤,勤能补拙!
8.1.2样本相关系数
形
数
活动:月考过后,有同学说自己以前基础差,所以这次考差了是可以理解的,大家怎么理解这位同学的话?
问题1:能否引入一个适当的类似期望与方差的数字特征,来度量样本数据的相关关系强弱?
即分析基础与现在成绩的关系
追问1:数据的中心在哪里?
追问2:数据中心化是否会影响数据的相关性
追问3:中心化的数据有什么特征?(形和数的角度)
追问4:基于我们的目标和中心化的前提,我们“创造”的数字特征该如何表达?
形的角度:
变量正相关时,中心化后的数据大多数在一、三象限
变量负相关时,中心化后的数据大多数在二、四象限
数的角度:
正相关,横纵坐标同号;
负相关,横纵坐标异号
大多数?
同异号?
累加
“同异号”
“大多数”
平移
形
数
问题2:从计算角度思考式子中存在的局限性
容易受样本数据的度量单位影响!
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,
则相应的????????????将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
?
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
称r为变量x和变量y的样本相关系数(Sample Correlation coefficient)
“标准化”
形
数
Bug:Lxy的大小受数据的度量单位的影响,但单位的改变并不会导致两个变量之间相关程度的改变.
r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本相关系数:
问题3:r的取值范围是什么?
强
强
弱
弱
思考:若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-2x+1上,问这组样本数据的样本相关系数?
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,
故|r|越接近1时,线性相关程度越强;
|r|越接近0时,线性相关程度越弱;
思考:若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-2x+1上,问这组样本数据的样本相关系数?
卡尔·皮尔逊,是英国数学家,生物统计学家,数理统计学的创立者,自由思想者,对生物统计学、气象学、社会达尔文主义理论和优生学做出了重大贡献。他被公认是旧派理学派和描述统计学派的代表人物,并被誉为现代统计科学的创立者。是20世纪科学革命和哲学革命的先驱,“批判学派”代表人物之一。
“统计是科学的语法”
追问:r=0是否反映成对数据没有关系?
活动:月考过后,有听到同学说自己以前基础差,所以这次考差了是可以理解的,大家认同这句话吗?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}各科不同阶段与中考成绩的样本相关系数
高一上
高二上
语文
0.56
0.71
数学
0.66
0.46
英语
0.81
0.47
活动:月考过后,有听到同学说自己以前基础差,所以这次考差了是可以理解的,大家认同这句话吗?
1.学科上来看,初中的英语对高中学习有较大影响,即初中英语好的同学,大概率高中入学英语也不错。
2.从不同年段角度分析,数学与英语学科随着高中学习时间的增加,高中成绩的好坏与初中基础的相关程度降低。
天道酬勤,勤能补拙
=
作业:
1.完成分层作业
2.思考本节课你感到最难的内容是什么?我们是怎么突破的?
3.尝试证明下式:
4.周末尝试借助EXCEL分析其他学科的成绩数据,并总结收获
思考:本节课你感到最难的内容是什么?我们是怎么突破的?
=
作业:
1.完成分层作业
2.尝试证明下式:
3.周末尝试借助EXCEL分析其他学科的成绩数据,并总结收获
回顾:期望与方差的反映了数据怎样的数字特征
均值反映了随机变量取值的平均水平.
即反映随机变量变量分布的中心趋势
方差与标准差反映随机变量取值的离散程度
注:方差与标准差的单位不同,后者与数据单位一致
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
