人教A版(2019)必修第二册 8.4.1平面 课件(共30张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册 8.4.1平面 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 18:12:27 | ||
图片预览






文档简介
8.4.1 平面
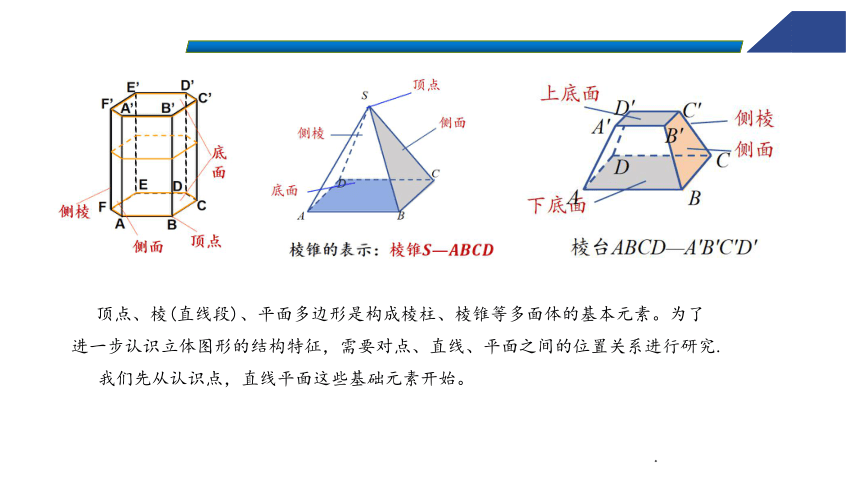
顶点、棱(直线段)、平面多边形是构成棱柱、棱锥等多面体的基本元素。为了进一步认识立体图形的结构特征,需要对点、直线、平面之间的位置关系进行研究.
我们先从认识点,直线平面这些基础元素开始。
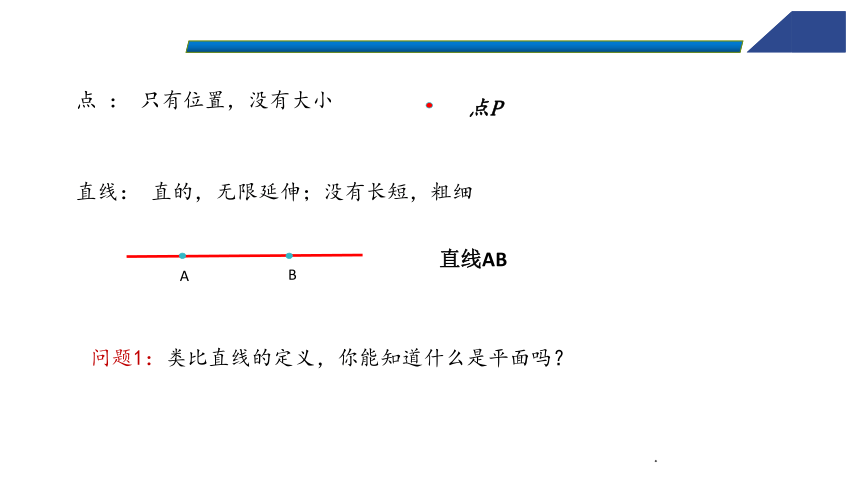
点 : 只有位置,没有大小
直线: 直的,无限延伸;没有长短,粗细
点P
A
B
直线AB
问题1:类比直线的定义,你能知道什么是平面吗?
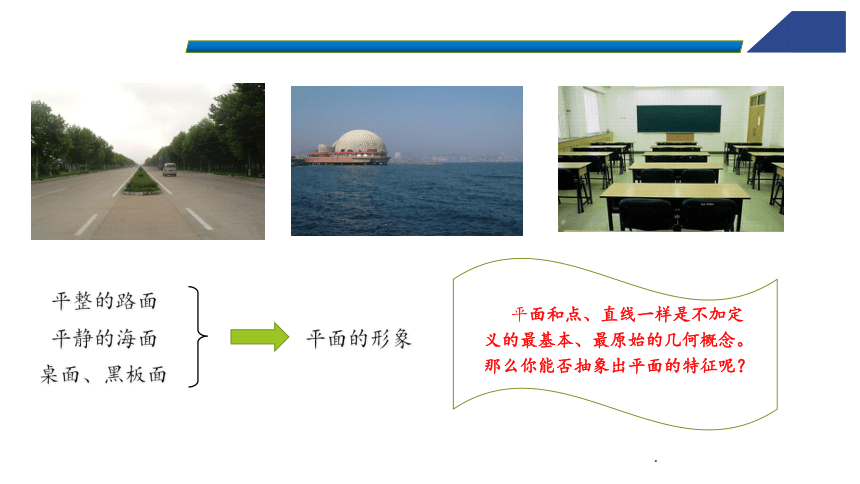
平整的路面
平静的海面
桌面、黑板面
平面的形象
平面和点、直线一样是不加定义的最基本、最原始的几何概念。那么你能否抽象出平面的特征呢?
几何里所说的“平面”(????????????????????)就是从这样的一些物体中抽象出来的,但是,几何里的平面是“平”的,无限延展的, 无薄厚之分 ,不计大小 .
?
问题2:如何用图形和符号表示平面?
直线的画法:画出直线的一部分来表示直线
平面的画法:画出平面的一部分来表示平面
类比生成
矩形直观图
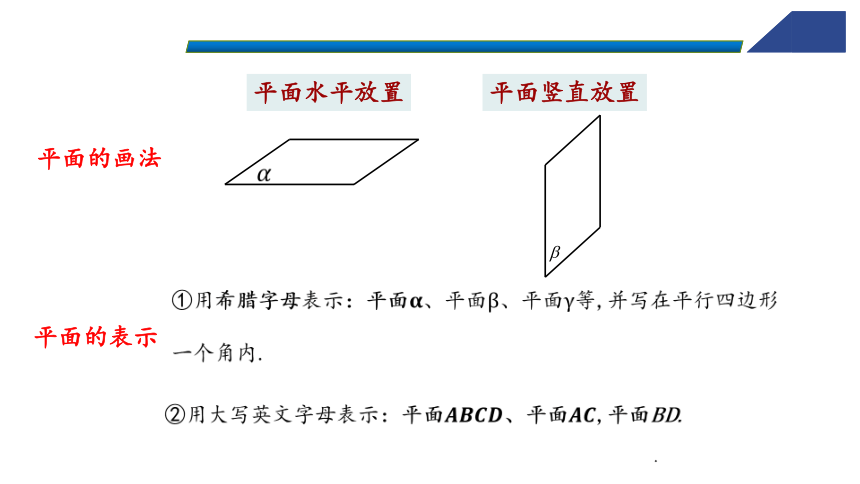
平面水平放置
平面竖直放置
????
?
平面的画法
①用希腊字母表示:平面????、平面β、平面γ等,并写在平行四边形一个角内.
?
②用大写英文字母表示:平面????????????????、平面????????,平面BD.
?
平面的表示
(1)古希腊时期的平面定义
早在公元前 5 世纪, 古希腊哲学家巴门尼德将平面定义为 “如果一个二维对象是直的表面, 那么它就是一个平面, 直线可在任意方向与之相合”。
这里, 巴门尼德将 “直” 作为平面的本质特征并利用直线来刻画这一特性, 其中强调平面是二维的, 是没有厚度的。
欧几里得将平面定义为 “与其上直线一样平放着的面”,这里欧几里得继续强调了用直线来刻画平面。
但巴门尼德和欧几里得的定义中用到了 “直” 和 “平放” 这些比较模糊的概念,定义还不精确。
平面概念发展的历史
(2)平面的包含式与构造性定义
18 世纪, 英国数学家辛松给出了平面的新定义: “平面是具有下列性质的面, 通过其上任意两点的直线完全包含在该面上。” 辛松的定义由于应用了 “直线包含于平面” 这一概念我们称之为平面的包含式定义。如 18 世纪法国数学家勒让德在其《几何与三角学基础》(1800)和苏格兰数学家普雷菲尔在《几何学基础》 (1829) 都采用此定义。
为了解决平面构造的问题, 数学家也给出了一系列平面的构造性定义。
德国数学家克雷尔给出平面的静态构造性定义: “平面是包含所有通过空间中一个定点并与另一条直线垂直的直线的面。”
法国数学家傅里叶给出了类似的定义: “平面由经过直线上一点且与直线垂直的所有直线构成。”
德国数学家莱布尼兹给出了平面的另一个构造性定义: “平面是与两点等距离的点的集合。”
匈牙利数学家 W·波尔约则采用动态的构造性定义: “平面是由一条直线绕着另一条与之垂直的直线旋转而成的面。”
动态构造定义与静态构造性本质上是相同的。
(3)平面的公理化定义 19 世纪末, 意大利数学家皮亚诺创立数学学派, 对算术和几何的公理化做出了巨大贡献, 其中的一名重要成员、意大利数学家皮埃里利用点、线段和运动对几何进行公理化。在此之后, 希尔伯特在其《几何基础》中建立了完全公理化的欧氏几何。希尔伯特可能受到当时数学抽象化和公理化趋势的影响, 并未对平面作出定义, 而将其作为一个基本的概念, 像点和直线一样。公理决定了基本概念之间的联系,概念的意义只有在公理中得到体现,因此,公理就起到了定义的作用。希尔伯特的公理被大部分数学家所接受, 同时也被数学教育界所接受, 大多数教科书也因此深受影响。现在教科书中平面的三大公理即由此而来。
思考1:我们知道,两点可以确定一条直线,那么几点可以确定一个平面?
基本事实1 过不在一条直线上的三个点,有且只有一个平面.
也可以简单说成:“不共线的三点确定一个平面”.
A
C
B
符号语言 A、B、C三点不共线?存在唯一的平面??????使????,????,???? ∈????
?
图形语言
应用: 基本事实1给出了确定一个平面的依据
问题3:直线、平面可以看成是点的集合,点线,点面之间有什么位置关系,
又应该如何表示?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形语言
文字语言
符号语言
???? 在 ???? 上
????∈????
???? 在 ???? 外
?????????
???? 在 α 内
????∈α
???? 在 α 外
?????α
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形语言
文字语言
符号语言
问题3:直线、平面可以看成是点的集合,点线,点面之间有什么位置关系,
又应该如何表示?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
直线 ???? 与平面????有一个公共点????,直线 ???? 不在平面????内
?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
直线 ???? 与平面????有两个公共点,直线在平面内
?
直线 ???? 与平面????有一个公共点????,直线 ???? 不在平面????内
?
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
α
l
A
B
图形语言
符号语言
应用: 利用基本事实2可以判断直线是否在平面内
问题4 平面具有“平”和“无限延展”的特征. 而基本事实2反映了直线与平面的位置关系、我们能不能利用这种位置关系,用直线的“直”和“无限延伸”刻画平面的“平”和“无限延展”?
思考3:如下图,把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点?????为什么?
?
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
符号语言
?
图形语言
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
符号语言 ????∈????,且????∈?????????∩????=????,且????∈????.
?
l
P
应用:
①判断两个平面相交的依据.(只要两个平面有公共点,就可以判定
这两个平面必相交于过这个点的一条直线)
②判断点在直线上.(点是某两个平面的公共点,线是这两个平面的公共交线,则这个点在交线上)
在画图时,如果图形的一部分被
另一部分遮住,可以把遮住部分
画成虚线,也可以不画.
图形语言
问题5:类似基本事实 2, 你能结合基本事实 3, 进一步说明平面的 “平” 和 “无线延展” 的基本特征吗?
l
P
平面是“平”的,因而两个相交平面才可能交于一条直线;否则交线就不是直的,而是曲的;
两个平面相交于一条直线,直线是无线延伸的,说明平面的交点由无数个,平面是“无限延展”的
问题6: 基本事实 1 给出了确定一个平面的一种方法. 利用基本事实1 和基本事实 2 ,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
问题6: 基本事实 1 给出了确定一个平面的一种方法. 利用基本事实1 和基本事实 2 ,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
α
?
????
?
A
推论1 经过一条直线和这条直线外一点,有且只有一个平面
α
?
b
????
?
b
P
P
P
推论2 经过两条相交直线,有且只有一个平面.
α
?
????
?
????
?
推论3 经过两条平行直线,有且只有一个平面.
几何之务,不在知其然而在知其所以然;
不在知其所以然,而在何由以知其所以然.
——著名数学家、教育家傅仲孙
顶点、棱(直线段)、平面多边形是构成棱柱、棱锥等多面体的基本元素。为了进一步认识立体图形的结构特征,需要对点、直线、平面之间的位置关系进行研究.
我们先从认识点,直线平面这些基础元素开始。
点 : 只有位置,没有大小
直线: 直的,无限延伸;没有长短,粗细
点P
A
B
直线AB
问题1:类比直线的定义,你能知道什么是平面吗?
平整的路面
平静的海面
桌面、黑板面
平面的形象
平面和点、直线一样是不加定义的最基本、最原始的几何概念。那么你能否抽象出平面的特征呢?
几何里所说的“平面”(????????????????????)就是从这样的一些物体中抽象出来的,但是,几何里的平面是“平”的,无限延展的, 无薄厚之分 ,不计大小 .
?
问题2:如何用图形和符号表示平面?
直线的画法:画出直线的一部分来表示直线
平面的画法:画出平面的一部分来表示平面
类比生成
矩形直观图
平面水平放置
平面竖直放置
????
?
平面的画法
①用希腊字母表示:平面????、平面β、平面γ等,并写在平行四边形一个角内.
?
②用大写英文字母表示:平面????????????????、平面????????,平面BD.
?
平面的表示
(1)古希腊时期的平面定义
早在公元前 5 世纪, 古希腊哲学家巴门尼德将平面定义为 “如果一个二维对象是直的表面, 那么它就是一个平面, 直线可在任意方向与之相合”。
这里, 巴门尼德将 “直” 作为平面的本质特征并利用直线来刻画这一特性, 其中强调平面是二维的, 是没有厚度的。
欧几里得将平面定义为 “与其上直线一样平放着的面”,这里欧几里得继续强调了用直线来刻画平面。
但巴门尼德和欧几里得的定义中用到了 “直” 和 “平放” 这些比较模糊的概念,定义还不精确。
平面概念发展的历史
(2)平面的包含式与构造性定义
18 世纪, 英国数学家辛松给出了平面的新定义: “平面是具有下列性质的面, 通过其上任意两点的直线完全包含在该面上。” 辛松的定义由于应用了 “直线包含于平面” 这一概念我们称之为平面的包含式定义。如 18 世纪法国数学家勒让德在其《几何与三角学基础》(1800)和苏格兰数学家普雷菲尔在《几何学基础》 (1829) 都采用此定义。
为了解决平面构造的问题, 数学家也给出了一系列平面的构造性定义。
德国数学家克雷尔给出平面的静态构造性定义: “平面是包含所有通过空间中一个定点并与另一条直线垂直的直线的面。”
法国数学家傅里叶给出了类似的定义: “平面由经过直线上一点且与直线垂直的所有直线构成。”
德国数学家莱布尼兹给出了平面的另一个构造性定义: “平面是与两点等距离的点的集合。”
匈牙利数学家 W·波尔约则采用动态的构造性定义: “平面是由一条直线绕着另一条与之垂直的直线旋转而成的面。”
动态构造定义与静态构造性本质上是相同的。
(3)平面的公理化定义 19 世纪末, 意大利数学家皮亚诺创立数学学派, 对算术和几何的公理化做出了巨大贡献, 其中的一名重要成员、意大利数学家皮埃里利用点、线段和运动对几何进行公理化。在此之后, 希尔伯特在其《几何基础》中建立了完全公理化的欧氏几何。希尔伯特可能受到当时数学抽象化和公理化趋势的影响, 并未对平面作出定义, 而将其作为一个基本的概念, 像点和直线一样。公理决定了基本概念之间的联系,概念的意义只有在公理中得到体现,因此,公理就起到了定义的作用。希尔伯特的公理被大部分数学家所接受, 同时也被数学教育界所接受, 大多数教科书也因此深受影响。现在教科书中平面的三大公理即由此而来。
思考1:我们知道,两点可以确定一条直线,那么几点可以确定一个平面?
基本事实1 过不在一条直线上的三个点,有且只有一个平面.
也可以简单说成:“不共线的三点确定一个平面”.
A
C
B
符号语言 A、B、C三点不共线?存在唯一的平面??????使????,????,???? ∈????
?
图形语言
应用: 基本事实1给出了确定一个平面的依据
问题3:直线、平面可以看成是点的集合,点线,点面之间有什么位置关系,
又应该如何表示?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形语言
文字语言
符号语言
???? 在 ???? 上
????∈????
???? 在 ???? 外
?????????
???? 在 α 内
????∈α
???? 在 α 外
?????α
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形语言
文字语言
符号语言
问题3:直线、平面可以看成是点的集合,点线,点面之间有什么位置关系,
又应该如何表示?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
直线 ???? 与平面????有一个公共点????,直线 ???? 不在平面????内
?
思考2:如果直线 ???? 与平面α有一个公共点????,直线 ???? 是否在平面????内?
如果直线 ???? 与平面α有两个公共点呢?
?
直线 ???? 与平面????有两个公共点,直线在平面内
?
直线 ???? 与平面????有一个公共点????,直线 ???? 不在平面????内
?
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
α
l
A
B
图形语言
符号语言
应用: 利用基本事实2可以判断直线是否在平面内
问题4 平面具有“平”和“无限延展”的特征. 而基本事实2反映了直线与平面的位置关系、我们能不能利用这种位置关系,用直线的“直”和“无限延伸”刻画平面的“平”和“无限延展”?
思考3:如下图,把三角尺的一个角立在课桌面上,三角尺所在平面与课桌面所在平面是否只相交于一点?????为什么?
?
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
符号语言
?
图形语言
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
符号语言 ????∈????,且????∈?????????∩????=????,且????∈????.
?
l
P
应用:
①判断两个平面相交的依据.(只要两个平面有公共点,就可以判定
这两个平面必相交于过这个点的一条直线)
②判断点在直线上.(点是某两个平面的公共点,线是这两个平面的公共交线,则这个点在交线上)
在画图时,如果图形的一部分被
另一部分遮住,可以把遮住部分
画成虚线,也可以不画.
图形语言
问题5:类似基本事实 2, 你能结合基本事实 3, 进一步说明平面的 “平” 和 “无线延展” 的基本特征吗?
l
P
平面是“平”的,因而两个相交平面才可能交于一条直线;否则交线就不是直的,而是曲的;
两个平面相交于一条直线,直线是无线延伸的,说明平面的交点由无数个,平面是“无限延展”的
问题6: 基本事实 1 给出了确定一个平面的一种方法. 利用基本事实1 和基本事实 2 ,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
问题6: 基本事实 1 给出了确定一个平面的一种方法. 利用基本事实1 和基本事实 2 ,再结合“两点确定一条直线”,你还可以得到一些确定一个平面的方法吗?
α
?
????
?
A
推论1 经过一条直线和这条直线外一点,有且只有一个平面
α
?
b
????
?
b
P
P
P
推论2 经过两条相交直线,有且只有一个平面.
α
?
????
?
????
?
推论3 经过两条平行直线,有且只有一个平面.
几何之务,不在知其然而在知其所以然;
不在知其所以然,而在何由以知其所以然.
——著名数学家、教育家傅仲孙
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
