湖北省黄石市第三中学2015-2016学年高二下学期期末考试数学(文)试题
文档属性
| 名称 | 湖北省黄石市第三中学2015-2016学年高二下学期期末考试数学(文)试题 | 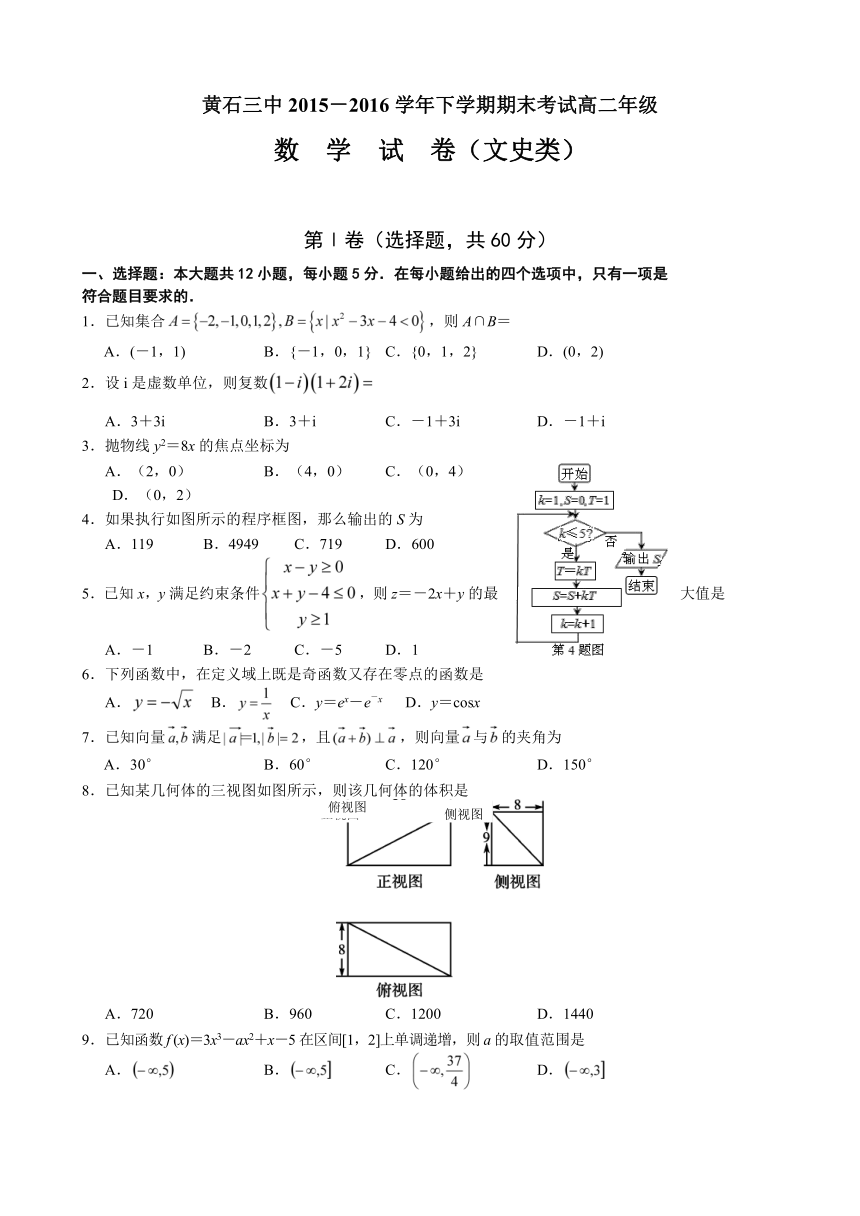 | |
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-02 22:15:46 | ||
图片预览



文档简介
黄石三中2015-2016学年下学期期末考试高二年级
数
学 试 卷(文史类)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合,则A∩B=
A.(-1,1)
B.{-1,0,1}
C.{0,1,2}
D.(0,2)
2.设i是虚数单位,则复数
A.3+3i
B.3+i
C.-1+3i
D.-1+i
3.抛物线y2=8x的焦点坐标为
A.(2,0)
B.(4,0)
C.(0,4)
D.(0,2)
4.如果执行如图所示的程序框图,那么输出的S为
A.119
B.4949
C.719
D.600
5.已知x,y满足约束条件,则z=-2x+y的最大值是
A.-1
B.-2
C.-5
D.1
6.下列函数中,在定义域上既是奇函数又存在零点的函数是
A.
B.
C.y=ex-e-x
D.y=cosx
7.已知向量满足,且,则向量与的夹角为
A.30°
B.60°
C.120°
D.150°
8.已知某几何体的三视图如图所示,则该几何体的体积是
A.720
B.960
C.1200
D.1440
9.已知函数f
(x)=3x3-ax2+x-5在区间[1,2]上单调递增,则a的取值范围是
A.
B.
C.
D.
10.同时具有性质“①最小正周期是,②图象关于直线对称”的一个函数是
A.
B.
C.
D.
11.下列有关命题的叙述错误的是
A.对于命题,则
B.若p∧q为假命题,则p,q均为假命题
C.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”
D.“x>2”是“x2-3x+2>0”的充分不必要条件
12.已知f
(x)是定义在R上的偶函数,对任意x∈R都有f
(x+6)=f
(x)+2f
(3),且f
(0)=3,则f
(2016)=
A.1
B.2
C.3
D.4
第Ⅱ卷(非选择题,共90分)
本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答.第22题—第24题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分.
13.若,且为第三象限角,则的值等于__________.
14.函数的定义域为__________.
15.设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a的值为__________.
16.若在区间(0,2)内任取两数,则椭圆的离心率大于的概率为__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知等差数列{an},满足a2=2,a4=4.
⑴求数列{an}的通项公式;
⑵求数列的前n项和.
18.(本小题满分12分)某校为了响应《
( http: / / www.21cnjy.com )中共中央国务院关于加强青少年体育增强青少年体质的意见》精神,落实“生命—和谐”教育理念和阳光体育行动的现代健康理念,学校特组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立的.成绩如下:(单位:个/分钟)
甲
80
81
93
72
88
75
83
84
乙
82
93
70
84
77
87
78
85
⑴用茎叶图表示这两组数据;
⑵从统计学的角度考虑,你认为选派哪位学生参加比赛合适,请说明理由;
⑶分别估计该班对甲乙两同学的成绩高于79个/分钟的概率.
(参考数据:
)
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
⑴求证:平面ABC1⊥平面A1ACC1;
⑵设D是线段BB1的中点,求三棱锥D-ABC1的体积.
20.(本小题满分12分)已知函数.
⑴求函数g(x)在x=e处的切线方程;
⑵a为何值时,函数y=f
(x)的图像与函数y=g(x)的图像有三个不同的交点.
21.(本小题满分12分)已知椭圆的左、右顶点分别为A1,A2,且,该椭圆的离心率为,以M(-3,2)为圆心,r为半径的圆与椭圆C交于A,B两点.
⑴求椭圆C的方程;
⑵若A,B两点关于原点对称,求圆M的方程;
⑶若点A的坐标为(0,2),求△ABM的面积.
请考生从第22、23、24题中任选一题作答,多答,则按所做的第一题记分.作答时请写清题号.
22.(本小题满分10分)选修4-1:几何证明选讲
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
⑴证明:EF∥BC;
⑵若AG等于⊙O的半径,且,求四边形EBCF的面积.
23.(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴的极坐标系中,曲线C:,直线l的参数方程:(t为参数),两曲线相交于M,N两点.
⑴写出曲线C的直角坐标方程和直线l的普通方程;
⑵若,求的值.
24.(本小题满分10分)选修4-5:不等式选讲
设函数,的最小值为m.
⑴求m的值;
⑵当时,求的最小值.
高二数学数学(文史类)答案
1.C
2.B
3.A
( http: / / www.21cnjy.com )4.C
5.A
6.C
7.C
8.C
9.B
10.D
11.B
12.C
13.
14.
15.
16.
17.解:⑴设等差数列的公差为d,则
解得,
∴,故an=n.
…………………………………6分
⑵,
…………………………………8分
故
=
=.
……………12分
18.解:⑴
……………4分
⑵
由于甲乙的平均成绩相等,而甲的方差较小,所以甲的成绩较稳定,派甲参赛比较合适
…8分
注:本小题的结论及理由不唯一,如果考生从统计学的角度分析,给出其他合理回答,同样给分;如派甲比较合适,理由如下:甲获得79个/分钟以上的概率为,乙获得79个/分钟以上的概率为.∵P1>P2,所以派甲参赛比较合适.
⑶甲获得79个/分钟以上的概率为,乙获得79个/分钟以上的概率为.
…………………………12分
19.⑴证明:在直三棱锥ABC—A1B1C1中,有A1A⊥面ABC,而面ABC,
∴A1A⊥AB,又A1A=AC
∴A1C⊥AC1,又BC1⊥A1C,,
BC1∩AC1=C1
∴A1C⊥面ABC1,而,则面ABC1⊥面A1ACC1
………6分
⑵在直三棱锥ABC—A1B1C1中,有A1A⊥面ABC,而面ABC,
∴A1A⊥AB,由⑴知A1C⊥面ABC1,A1C⊥AB,故AB⊥面,AB⊥AC,
则有AC⊥面ABB1A1,因为是线段的中,则.
…………………………12分
20.⑴由得g(e)=4,,
,
故函数g(x)在x=e处的切线方程为y-4=(x―e)
即.
…………………………4分
⑵令h(x)=g(x)―f
(x)=4lnx+x2―6x+a
(x>0)
则
=,
令
(x>0)
则
02,
令
(x>0)
则
1故h(x)在(0,1)上递增,(1,2)上递减,(2,+∞)上递增.
…………………………8分
要使的图像与函数的图像有三个不同的交点
则,
即解得,
故5………………………………12分
21.⑴由题意可知2a=4,即a=2,又,则,b2=4,
即椭圆C的方程为.
…………………………………4分
⑵因为A,B两点关于原点对称,所以O是AB的中点,由垂径定理可知MO⊥AB,又M(-3,2),所以直线MO的斜率为-,故直线AB的斜率为,则直线AB的方程为y=x,联立解得,由勾股定理得r2=MA2=MO2+OA2=9+4+,
所以圆M的方程为(x+3)2+(y-2)2=.
……………………………8分
⑶显然直线AB的斜率存在,设直线AB的方程为y=kx+2,联立得(1+3k2)x2+12kx=0,
则B(),线段AB的中点为E(),直线ME的斜率为
,∵AB⊥ME,∴·k=-1
∴(k-1)(2k2-k+1)=0,解得k=1,所以直线AB的方程为y=x+2,
B(-3,-1),所以|AB|=3,点M到直线AB的距离为,
故△ABM的面积为.
………………………………12分
22.解:⑴由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线,
又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF,
从而EF∥BC.
……………………5分
⑵由⑴知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为
⊙O的弦,所以O在AD上,连结OE,OM,则OE⊥AE,
由AG等于⊙O的半径,得AO=2OE,所以∠OAE=30°,
因此△ABC和△AEF都是等边三角形,
因为,所以AO=4,OE=2,
因为OM=OE=2,,所以OD=1,
于是AD=5,,
所以四边形EBCF的面积为.
……………………10分
23.⑴曲线C的直角坐标方程为y2=4x,直线l的普通方程为x-y-2=0.
……………………5分
⑵直线l的参数方程(t为参数)代入y2=4x,得到t2-12t+48=0,得M,N对应的参数分别为t1,t2,则t1+t2=12,t1t2=48>0,
∴|PM|+|PN|=|t1|+|t2|=|t1+t2|=12.
……………………10分
另解:由联立解得:.由两点间距离公式,得:|PM|+|PN|=12.
……………………10分
24.⑴f
(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1
(3≤x≤4时取等号)
故f
(x)的最小值为1,即m=1.
……………………5分
⑵(a2+b2+c2)·(12+22+32)≥(a+2b+3c)2=1,
故a2+b2+c2
当且仅当a=,b=,c=时取等号,
∴a2+b2+c2的最小值为.
……………………10分
正视图
侧视图
俯视图
B
D
·
C1
A1
B1
A
C
G
A
E
F
O
N
D
B
C
M
甲
乙
3
9
3
8
4
3
1
0
8
2
4
5
7
5
2
7
0
7
8
数
学 试 卷(文史类)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合,则A∩B=
A.(-1,1)
B.{-1,0,1}
C.{0,1,2}
D.(0,2)
2.设i是虚数单位,则复数
A.3+3i
B.3+i
C.-1+3i
D.-1+i
3.抛物线y2=8x的焦点坐标为
A.(2,0)
B.(4,0)
C.(0,4)
D.(0,2)
4.如果执行如图所示的程序框图,那么输出的S为
A.119
B.4949
C.719
D.600
5.已知x,y满足约束条件,则z=-2x+y的最大值是
A.-1
B.-2
C.-5
D.1
6.下列函数中,在定义域上既是奇函数又存在零点的函数是
A.
B.
C.y=ex-e-x
D.y=cosx
7.已知向量满足,且,则向量与的夹角为
A.30°
B.60°
C.120°
D.150°
8.已知某几何体的三视图如图所示,则该几何体的体积是
A.720
B.960
C.1200
D.1440
9.已知函数f
(x)=3x3-ax2+x-5在区间[1,2]上单调递增,则a的取值范围是
A.
B.
C.
D.
10.同时具有性质“①最小正周期是,②图象关于直线对称”的一个函数是
A.
B.
C.
D.
11.下列有关命题的叙述错误的是
A.对于命题,则
B.若p∧q为假命题,则p,q均为假命题
C.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”
D.“x>2”是“x2-3x+2>0”的充分不必要条件
12.已知f
(x)是定义在R上的偶函数,对任意x∈R都有f
(x+6)=f
(x)+2f
(3),且f
(0)=3,则f
(2016)=
A.1
B.2
C.3
D.4
第Ⅱ卷(非选择题,共90分)
本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答.第22题—第24题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分.
13.若,且为第三象限角,则的值等于__________.
14.函数的定义域为__________.
15.设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a的值为__________.
16.若在区间(0,2)内任取两数,则椭圆的离心率大于的概率为__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知等差数列{an},满足a2=2,a4=4.
⑴求数列{an}的通项公式;
⑵求数列的前n项和.
18.(本小题满分12分)某校为了响应《
( http: / / www.21cnjy.com )中共中央国务院关于加强青少年体育增强青少年体质的意见》精神,落实“生命—和谐”教育理念和阳光体育行动的现代健康理念,学校特组织“踢毽球”大赛,某班为了选出一人参加比赛,对班上甲乙两位同学进行了8次测试,且每次测试之间是相互独立的.成绩如下:(单位:个/分钟)
甲
80
81
93
72
88
75
83
84
乙
82
93
70
84
77
87
78
85
⑴用茎叶图表示这两组数据;
⑵从统计学的角度考虑,你认为选派哪位学生参加比赛合适,请说明理由;
⑶分别估计该班对甲乙两同学的成绩高于79个/分钟的概率.
(参考数据:
)
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
⑴求证:平面ABC1⊥平面A1ACC1;
⑵设D是线段BB1的中点,求三棱锥D-ABC1的体积.
20.(本小题满分12分)已知函数.
⑴求函数g(x)在x=e处的切线方程;
⑵a为何值时,函数y=f
(x)的图像与函数y=g(x)的图像有三个不同的交点.
21.(本小题满分12分)已知椭圆的左、右顶点分别为A1,A2,且,该椭圆的离心率为,以M(-3,2)为圆心,r为半径的圆与椭圆C交于A,B两点.
⑴求椭圆C的方程;
⑵若A,B两点关于原点对称,求圆M的方程;
⑶若点A的坐标为(0,2),求△ABM的面积.
请考生从第22、23、24题中任选一题作答,多答,则按所做的第一题记分.作答时请写清题号.
22.(本小题满分10分)选修4-1:几何证明选讲
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
⑴证明:EF∥BC;
⑵若AG等于⊙O的半径,且,求四边形EBCF的面积.
23.(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴的极坐标系中,曲线C:,直线l的参数方程:(t为参数),两曲线相交于M,N两点.
⑴写出曲线C的直角坐标方程和直线l的普通方程;
⑵若,求的值.
24.(本小题满分10分)选修4-5:不等式选讲
设函数,的最小值为m.
⑴求m的值;
⑵当时,求的最小值.
高二数学数学(文史类)答案
1.C
2.B
3.A
( http: / / www.21cnjy.com )4.C
5.A
6.C
7.C
8.C
9.B
10.D
11.B
12.C
13.
14.
15.
16.
17.解:⑴设等差数列的公差为d,则
解得,
∴,故an=n.
…………………………………6分
⑵,
…………………………………8分
故
=
=.
……………12分
18.解:⑴
……………4分
⑵
由于甲乙的平均成绩相等,而甲的方差较小,所以甲的成绩较稳定,派甲参赛比较合适
…8分
注:本小题的结论及理由不唯一,如果考生从统计学的角度分析,给出其他合理回答,同样给分;如派甲比较合适,理由如下:甲获得79个/分钟以上的概率为,乙获得79个/分钟以上的概率为.∵P1>P2,所以派甲参赛比较合适.
⑶甲获得79个/分钟以上的概率为,乙获得79个/分钟以上的概率为.
…………………………12分
19.⑴证明:在直三棱锥ABC—A1B1C1中,有A1A⊥面ABC,而面ABC,
∴A1A⊥AB,又A1A=AC
∴A1C⊥AC1,又BC1⊥A1C,,
BC1∩AC1=C1
∴A1C⊥面ABC1,而,则面ABC1⊥面A1ACC1
………6分
⑵在直三棱锥ABC—A1B1C1中,有A1A⊥面ABC,而面ABC,
∴A1A⊥AB,由⑴知A1C⊥面ABC1,A1C⊥AB,故AB⊥面,AB⊥AC,
则有AC⊥面ABB1A1,因为是线段的中,则.
…………………………12分
20.⑴由得g(e)=4,,
,
故函数g(x)在x=e处的切线方程为y-4=(x―e)
即.
…………………………4分
⑵令h(x)=g(x)―f
(x)=4lnx+x2―6x+a
(x>0)
则
=,
令
(x>0)
则
0
令
(x>0)
则
1
…………………………8分
要使的图像与函数的图像有三个不同的交点
则,
即解得,
故5
21.⑴由题意可知2a=4,即a=2,又,则,b2=4,
即椭圆C的方程为.
…………………………………4分
⑵因为A,B两点关于原点对称,所以O是AB的中点,由垂径定理可知MO⊥AB,又M(-3,2),所以直线MO的斜率为-,故直线AB的斜率为,则直线AB的方程为y=x,联立解得,由勾股定理得r2=MA2=MO2+OA2=9+4+,
所以圆M的方程为(x+3)2+(y-2)2=.
……………………………8分
⑶显然直线AB的斜率存在,设直线AB的方程为y=kx+2,联立得(1+3k2)x2+12kx=0,
则B(),线段AB的中点为E(),直线ME的斜率为
,∵AB⊥ME,∴·k=-1
∴(k-1)(2k2-k+1)=0,解得k=1,所以直线AB的方程为y=x+2,
B(-3,-1),所以|AB|=3,点M到直线AB的距离为,
故△ABM的面积为.
………………………………12分
22.解:⑴由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线,
又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF,
从而EF∥BC.
……………………5分
⑵由⑴知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为
⊙O的弦,所以O在AD上,连结OE,OM,则OE⊥AE,
由AG等于⊙O的半径,得AO=2OE,所以∠OAE=30°,
因此△ABC和△AEF都是等边三角形,
因为,所以AO=4,OE=2,
因为OM=OE=2,,所以OD=1,
于是AD=5,,
所以四边形EBCF的面积为.
……………………10分
23.⑴曲线C的直角坐标方程为y2=4x,直线l的普通方程为x-y-2=0.
……………………5分
⑵直线l的参数方程(t为参数)代入y2=4x,得到t2-12t+48=0,得M,N对应的参数分别为t1,t2,则t1+t2=12,t1t2=48>0,
∴|PM|+|PN|=|t1|+|t2|=|t1+t2|=12.
……………………10分
另解:由联立解得:.由两点间距离公式,得:|PM|+|PN|=12.
……………………10分
24.⑴f
(x)=|x-4|+|x-3|≥|(x-4)-(x-3)|=1
(3≤x≤4时取等号)
故f
(x)的最小值为1,即m=1.
……………………5分
⑵(a2+b2+c2)·(12+22+32)≥(a+2b+3c)2=1,
故a2+b2+c2
当且仅当a=,b=,c=时取等号,
∴a2+b2+c2的最小值为.
……………………10分
正视图
侧视图
俯视图
B
D
·
C1
A1
B1
A
C
G
A
E
F
O
N
D
B
C
M
甲
乙
3
9
3
8
4
3
1
0
8
2
4
5
7
5
2
7
0
7
8
同课章节目录
