1.3 第3课时 全等三角形的判定“角角边”(17张ppt)2025-2026学年数学苏科版八年级上册
文档属性
| 名称 | 1.3 第3课时 全等三角形的判定“角角边”(17张ppt)2025-2026学年数学苏科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 18:20:06 | ||
图片预览




文档简介
1.3 第3课时 全等三角形的判定 “角角边”
1.探索并掌握三角形全等的“角角边”条件,能用其证明三角形中的边或角相等
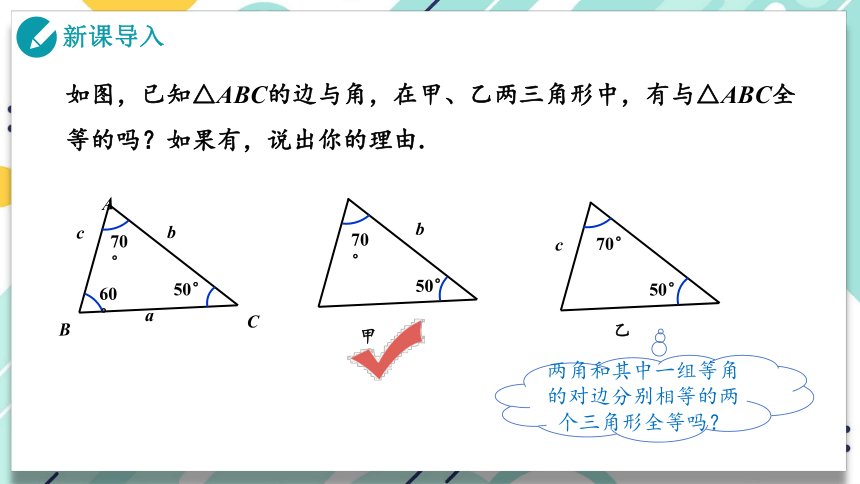
如图,已知△ABC的边与角,在甲、乙两三角形中,有与△ABC全等的吗?如果有,说出你的理由.
70°
50°
b
甲
70°
50°
c
乙
B
A
C
a
60°
50°
b
c
70°
两角和其中一组等角的对边分别相等的两个三角形全等吗?
如图,在△ABC 和△A′B′C′中,∠A=∠A′,∠C=∠C′,AB=A′B′,△ABC 与△A′B′C′全等吗?
A
B
C
A′
B′
C′
证明:在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△A′B′C′(ASA ).
∴ ∠B=180°-∠A-∠C.
同理 ∠B′=180°-∠A′-∠C′.
又∵∠A=∠A′,∠C=∠C′,
∴ ∠B=∠B′.
在△ABC和△A′B′C′中,
∠????=∠????′,????????=????′????′,∠????=∠????′.
?
根据三角形内角和定理,可知∠B = ∠B′
可由“ASA”证明△ABC 与△A′B′C′全等
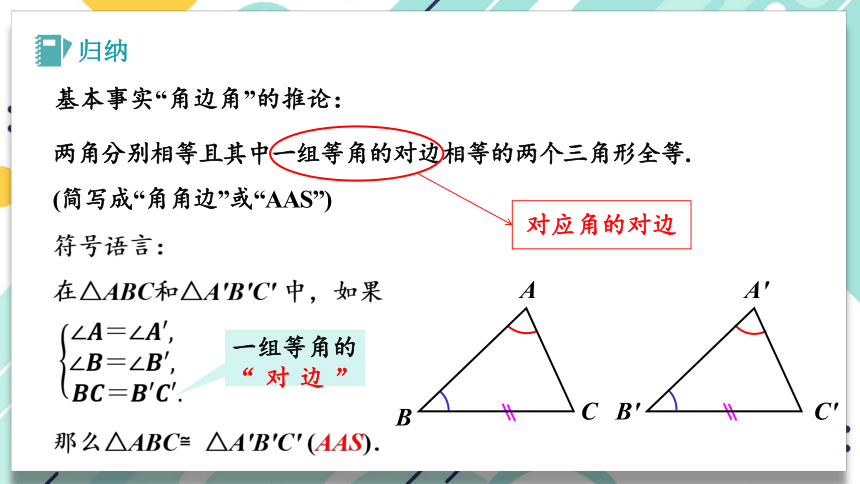
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(简写成“角角边”或“AAS”)
基本事实“角边角”的推论:
对应角的对边
符号语言:
在△ABC和△A′B′C′ 中,如果
∠????=∠????′,?∠????=∠????′,?????????=????′????′.
那么△ABC≌△A′B′C′ (AAS).
?
A
B
C
A′
B′
C′
一组等角的 “对边”
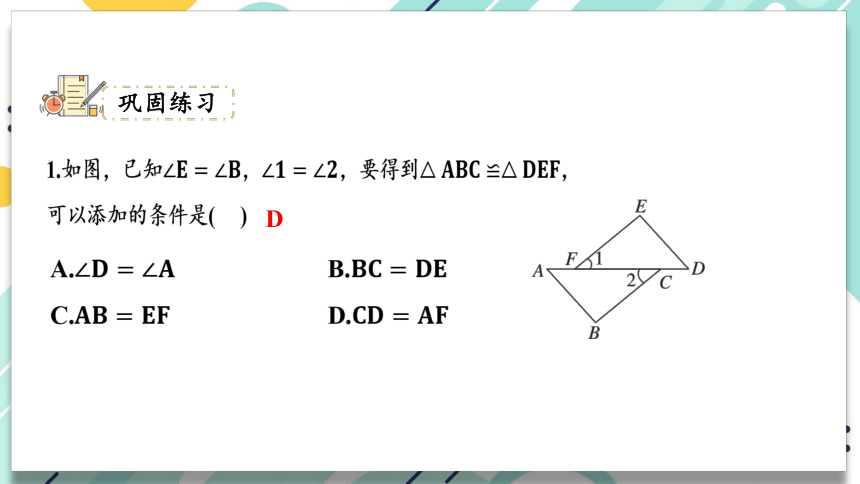
1.如图,已知∠????=∠???? ,∠????=∠????,要得到△????????????≌△???????????? ,
可以添加的条件是( )
?
D
A.∠????=∠???? B.????????=????????
C.????????=???????? D.????????=????????
?
巩固练习
“ASA”与“AAS”有什么区别和联系?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
区别
联系
“S”的意义
书写格式
ASA
AAS
“S”是两角的夹边.
“S”是其中一角的对边.
把夹边相等写在两角相等的中间.
把两角相等写在一起,边相等写在最后.
由三角形内角和定理可知,“AAS”可由“ASA”推导得出.
交流讨论
如图,△ABC≌△A?B?C?,AD,A?D?分别是△ABC和△A?B?C?的高.
求证:AD=A?D?.
A
B
C
D
A′
B′
C′
D′
要证AD=A'D',只要证△ABD≌△A' B'D'.
↑
两角及一角的对边
?
“AAS”证明
∠ADB=∠A′D′B′=90°
AB=A′B′
∠B=∠B′
?
由已知条件→
?
证明:∵ △ABC≌△A?B?C? ,
∴AB=A?B?,∠B=∠B? .
∵AD、A?D?分别是△ABC和△ A?B?C?的高,
∴∠ADB=∠A?D?B? = 90°.
在△ABD和△A?B?D?中,
∠????=∠?????,???????∠????????????=∠????????????????,?????????=??????????,?????????
△ABD≌△A?B?D?(AAS),
∴AD=A?D? .
?
如图,△ABC≌△A?B?C?,AD,A?D?分别是△ABC和△A?B?C?的高.
求证:AD=A?D?.
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? ,
∴AB=A?B?,∠B=∠B?,∠BAC=∠B?A?C? .
∵ AD、A?D?分别是△ABC和△ A?B?C?的角平分线,∴ ∠BAD= ????????∠BAC,∠B?A?D?=????????B?A?C? ,
∴ ∠BAD=∠B?A?D?.
在△ABD和△ A?B?D?中,
?∠????=∠?????,????????=??????????,∠????????????=∠????????????????,?
△ABC≌△A?B?C?(ASA),
∴AD=A?D?.
?
若AD,A?D?分别是△ABC和△ A?B?C?的角平分线,AD与A?D?相等吗?
A
B
C
D
A′
B′
C′
D′
探究
证△ABD≌△A' B'D'→AD=A'D'
?
“ASA”→
?
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? ,
∴AB=A?B?,∠B=∠B? ,BC=B?C? .
∵ AD、A?D?分别是△ABC和△ A?B?C?的中线,
∴ BD=????????BC,B?D?=???????? B?C? ,
∴ BD=B?D? .
在△ABD和△ A?B?D?中,
????????=??????????,?∠????=∠?????,?????????=???????????,???
△ABC≌△ A?B?C?(SAS),
∴AD=A?D?.
?
全等三角形的对应高、对应角平分线、对应中线相等.
归纳
若AD,A?D?分别是△ABC和△ A?B?C?的中线,AD与A?D?相等吗?
探究
证△ABD≌△A' B'D'→AD=A'D'
?
“SAS”→
?
2.如图,点????,????在????????上,∠????=∠????,∠????=∠???? ,
????????=????????.求证:????????=???????? .
?
证明:在△????????????和△????????????中,&∠????=∠????,&∠????=∠????,&????????=????????,
∴△????????????≌△????????????(????????????),
∴????????=???????? ,
∴?????????????????=?????????????????,即????????=???????? .
?
巩固练习
AAS判定
条件
两角+对应角的对边
应用
(先找角再找边,确认边是对应角的对边)
全等三角形对应高、中线、角平分线相等.
1.如图所示,已知∠????=∠???? ,则不一定能使
△????????????≌△???????????? 的条件是( )
?
B
A.????????=???????? B.????????=????????
C.∠????=∠???? D.????????平分∠????????????
?
2.如图,已知△????????????的六个元素,则甲、乙、丙三个三角形中和△????????????
全等的是( )
?
B
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
∠????????????=∠????????????
?
∠????=∠????
?
3.如图,已知点????,????,????,???? 在同一条直线上,∠????=∠????????????,????????=???????? ,现要说明△????????????≌△????????????,若要以“???????????? ”为依据,还需添加条件_______________;若要以“???????????? ”为依据,还需添加条件__________.
?
4. 如图,∠????=∠????=????????? ,∠????????????=∠???????????? .
(1)求证:△????????????≌△???????????? ;
(2)若∠????????????=????????? ,则∠????????????=____?? .
?
证明:(1)在△????????????和△????????????中,&∠????=∠????=?????????,&∠????????????=∠????????????,&????????=????????,
∴△????????????≌△????????????(????????????) .
?
20
1.探索并掌握三角形全等的“角角边”条件,能用其证明三角形中的边或角相等
如图,已知△ABC的边与角,在甲、乙两三角形中,有与△ABC全等的吗?如果有,说出你的理由.
70°
50°
b
甲
70°
50°
c
乙
B
A
C
a
60°
50°
b
c
70°
两角和其中一组等角的对边分别相等的两个三角形全等吗?
如图,在△ABC 和△A′B′C′中,∠A=∠A′,∠C=∠C′,AB=A′B′,△ABC 与△A′B′C′全等吗?
A
B
C
A′
B′
C′
证明:在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△A′B′C′(ASA ).
∴ ∠B=180°-∠A-∠C.
同理 ∠B′=180°-∠A′-∠C′.
又∵∠A=∠A′,∠C=∠C′,
∴ ∠B=∠B′.
在△ABC和△A′B′C′中,
∠????=∠????′,????????=????′????′,∠????=∠????′.
?
根据三角形内角和定理,可知∠B = ∠B′
可由“ASA”证明△ABC 与△A′B′C′全等
两角分别相等且其中一组等角的对边相等的两个三角形全等.
(简写成“角角边”或“AAS”)
基本事实“角边角”的推论:
对应角的对边
符号语言:
在△ABC和△A′B′C′ 中,如果
∠????=∠????′,?∠????=∠????′,?????????=????′????′.
那么△ABC≌△A′B′C′ (AAS).
?
A
B
C
A′
B′
C′
一组等角的 “对边”
1.如图,已知∠????=∠???? ,∠????=∠????,要得到△????????????≌△???????????? ,
可以添加的条件是( )
?
D
A.∠????=∠???? B.????????=????????
C.????????=???????? D.????????=????????
?
巩固练习
“ASA”与“AAS”有什么区别和联系?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
区别
联系
“S”的意义
书写格式
ASA
AAS
“S”是两角的夹边.
“S”是其中一角的对边.
把夹边相等写在两角相等的中间.
把两角相等写在一起,边相等写在最后.
由三角形内角和定理可知,“AAS”可由“ASA”推导得出.
交流讨论
如图,△ABC≌△A?B?C?,AD,A?D?分别是△ABC和△A?B?C?的高.
求证:AD=A?D?.
A
B
C
D
A′
B′
C′
D′
要证AD=A'D',只要证△ABD≌△A' B'D'.
↑
两角及一角的对边
?
“AAS”证明
∠ADB=∠A′D′B′=90°
AB=A′B′
∠B=∠B′
?
由已知条件→
?
证明:∵ △ABC≌△A?B?C? ,
∴AB=A?B?,∠B=∠B? .
∵AD、A?D?分别是△ABC和△ A?B?C?的高,
∴∠ADB=∠A?D?B? = 90°.
在△ABD和△A?B?D?中,
∠????=∠?????,???????∠????????????=∠????????????????,?????????=??????????,?????????
△ABD≌△A?B?D?(AAS),
∴AD=A?D? .
?
如图,△ABC≌△A?B?C?,AD,A?D?分别是△ABC和△A?B?C?的高.
求证:AD=A?D?.
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? ,
∴AB=A?B?,∠B=∠B?,∠BAC=∠B?A?C? .
∵ AD、A?D?分别是△ABC和△ A?B?C?的角平分线,∴ ∠BAD= ????????∠BAC,∠B?A?D?=????????B?A?C? ,
∴ ∠BAD=∠B?A?D?.
在△ABD和△ A?B?D?中,
?∠????=∠?????,????????=??????????,∠????????????=∠????????????????,?
△ABC≌△A?B?C?(ASA),
∴AD=A?D?.
?
若AD,A?D?分别是△ABC和△ A?B?C?的角平分线,AD与A?D?相等吗?
A
B
C
D
A′
B′
C′
D′
探究
证△ABD≌△A' B'D'→AD=A'D'
?
“ASA”→
?
A
B
C
D
A′
B′
C′
D′
证明:∵ △ABC≌△ A?B?C? ,
∴AB=A?B?,∠B=∠B? ,BC=B?C? .
∵ AD、A?D?分别是△ABC和△ A?B?C?的中线,
∴ BD=????????BC,B?D?=???????? B?C? ,
∴ BD=B?D? .
在△ABD和△ A?B?D?中,
????????=??????????,?∠????=∠?????,?????????=???????????,???
△ABC≌△ A?B?C?(SAS),
∴AD=A?D?.
?
全等三角形的对应高、对应角平分线、对应中线相等.
归纳
若AD,A?D?分别是△ABC和△ A?B?C?的中线,AD与A?D?相等吗?
探究
证△ABD≌△A' B'D'→AD=A'D'
?
“SAS”→
?
2.如图,点????,????在????????上,∠????=∠????,∠????=∠???? ,
????????=????????.求证:????????=???????? .
?
证明:在△????????????和△????????????中,&∠????=∠????,&∠????=∠????,&????????=????????,
∴△????????????≌△????????????(????????????),
∴????????=???????? ,
∴?????????????????=?????????????????,即????????=???????? .
?
巩固练习
AAS判定
条件
两角+对应角的对边
应用
(先找角再找边,确认边是对应角的对边)
全等三角形对应高、中线、角平分线相等.
1.如图所示,已知∠????=∠???? ,则不一定能使
△????????????≌△???????????? 的条件是( )
?
B
A.????????=???????? B.????????=????????
C.∠????=∠???? D.????????平分∠????????????
?
2.如图,已知△????????????的六个元素,则甲、乙、丙三个三角形中和△????????????
全等的是( )
?
B
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
∠????????????=∠????????????
?
∠????=∠????
?
3.如图,已知点????,????,????,???? 在同一条直线上,∠????=∠????????????,????????=???????? ,现要说明△????????????≌△????????????,若要以“???????????? ”为依据,还需添加条件_______________;若要以“???????????? ”为依据,还需添加条件__________.
?
4. 如图,∠????=∠????=????????? ,∠????????????=∠???????????? .
(1)求证:△????????????≌△???????????? ;
(2)若∠????????????=????????? ,则∠????????????=____?? .
?
证明:(1)在△????????????和△????????????中,&∠????=∠????=?????????,&∠????????????=∠????????????,&????????=????????,
∴△????????????≌△????????????(????????????) .
?
20
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
