1.3 第6课时 直角三角形全等的判定(16张ppt)2025-2026学年数学苏科版八年级上册
文档属性
| 名称 | 1.3 第6课时 直角三角形全等的判定(16张ppt)2025-2026学年数学苏科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 969.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 18:25:09 | ||
图片预览





文档简介
1.3 第6课时 直角三角形全等的判定
直角三角形是特殊三角形,判断两个直角三角形全等除了“SAS” “SSS” “ASA” “AAS”,还有没有特殊的方法?
SAS
ASA
AAS
AAS
三角形全等的判定需要三个条件,因为直角相等,所以还需要两个条件.
两个锐角相等可以吗?
两条边呢?
1.掌握用HL判定两个三角形全等的方法;
2.能用HL证明三角形中的边或角相等.
如图,给定直角三角形ABC (Rt△ABC),在透明纸上用直尺和圆规作△A'B'C′,使∠C'为直角,A'C'=AC,A'B'=AB.
B
C
A
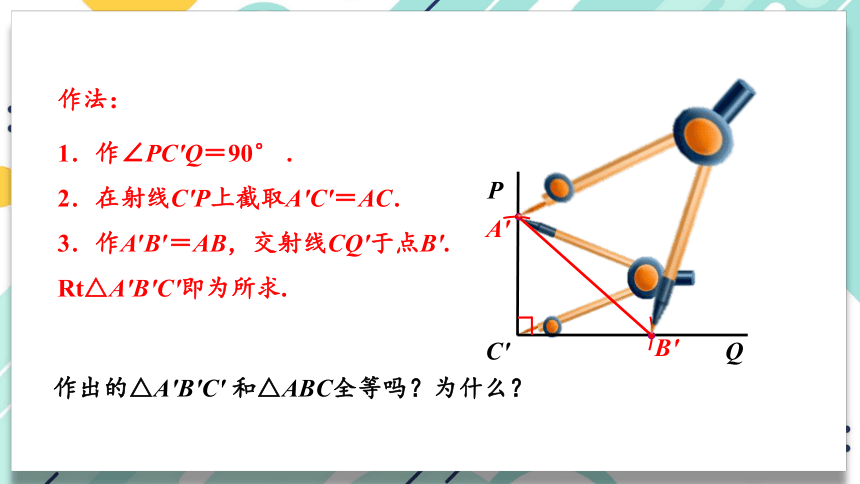
作法:
1.作∠PC′Q=90° .
2.在射线C′P上截取A′C′=AC.
3.作A′B′=AB,交射线CQ'于点B'.
Rt△A'B′C′即为所求.
Q
C′
P
A′
B′
作出的△A′B′C′ 和△ABC全等吗?为什么?
B
C
A
C′
B′
A′
P
Q
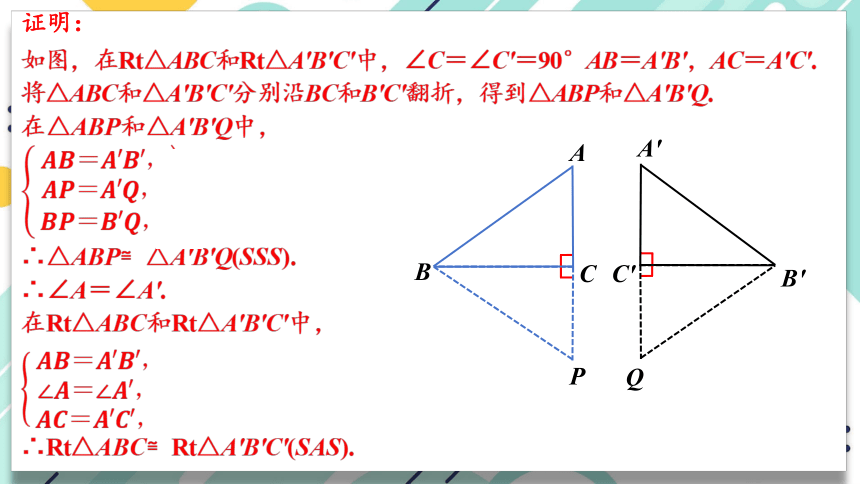
如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°AB=A′B′,AC=A′C′.
将△ABC和△A′B′C′分别沿BC和B′C′翻折,得到△ABP和△A'B′Q.
在△ABP和△A'B′Q中,
?????????=????′????′,????????=????′????,????????=????′????,
∴△ABP≌△A'B′Q(SSS).
∴∠A=∠A'.
在Rt△ABC和Rt△A'B′C′中,
?????????=????′????′,∠????=∠????′,????????=????′????′,
∴Rt△ABC≌Rt△A'B′C′(SAS).
?
证明:
判定两个直角三角形全等的定理:斜边和一条直角边分别相等的两个直角三角形全等.简记成“HL”.
符号语言:在 Rt△ABC 与 Rt△A'B'C' 中,∠C=∠C′=90°,如果
AC = A'C'
AB = A'B'
那么 Rt△ABC ≌ Rt△A'B'C' ( HL )
B'
A'
C'
B
A
C
不要丢了
1.如图,要用“????????”判定????????△????????????和????????△????′????′????′ 全等的条件可以是( )
?
C
A.????????=????′????′,????????=????′????′
B.∠????=∠????′,????????=????′????′
C.????????=????′????′,????????=????′????′
D.∠????=∠????′,????????=????′????′
?
活学活用
证明: ∵∠BAC=∠CDB=90°,
AC=DB,
BC=CB .
在 Rt△BCD 和Rt△CBA中,
∴ Rt△BCD≌Rt△CBA (HL).
B
C
A
D
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
例1 如图,∠BAC=∠CDB=90°, AC﹦DB,求证:AB﹦DC.
∴△BAC,△CDB都是直角三角形.
∴ AB﹦DC.
例2 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
A
D
C
B
O
分析:
1. AO与BO,CO与DO分别属于哪两个三角形?
2.证△ACO≌△BDO已有哪些条件?还缺什么条件?
3. AC、BD还属于哪两个三角形?
证明:在△ABC 和△BAD 中,∠C=∠D=90°,
????????=?????????,????????=????????,
∴ Rt△ABC≌Rt△BAD (HL).
∴ AC=BD.
在△AOC 和△BOD 中,
∠????=∠????,∠????????????=∠????????????,?????????=????????,???
∴△AOC≌△BOD,
∴AO=BO,CO=DO.
?
A
D
C
B
O
例2 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中, ????????=????????,????????=????????,?
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中, ????????=????????,????????=????????,?
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
?
活学活用
HL判定
条件
斜边+一条直角边(隐含条件:直角相等)
作图验证
应用
A
1.如图,????????⊥????????,????????⊥???????? ,????????=????????,能直接判断????????△????????????≌????????△???????????? 的理由是( )
A.???????? B.???????????? C.???????????? D.????????????
?
2.已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.求证:AB//DC.
A
B
C
D
O
证明:∵ AC⊥BD于点O,
∴∠AOB=∠DOC=90°,
∴△AOB和△COD都是直角三角形,
∵ OA=OC,AB=CD.
∴△AOB≌△COD(HL)
∴∠A=∠C
∴AB//DC.
A
F
C
E
D
B
3.如图,AB=CD ,BF⊥AC ,DE⊥AC ,AE=CF. 求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,
AB=CD,
AF=CE.
∴ Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
∴∠BFA=∠DEC=90 °.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
直角三角形是特殊三角形,判断两个直角三角形全等除了“SAS” “SSS” “ASA” “AAS”,还有没有特殊的方法?
SAS
ASA
AAS
AAS
三角形全等的判定需要三个条件,因为直角相等,所以还需要两个条件.
两个锐角相等可以吗?
两条边呢?
1.掌握用HL判定两个三角形全等的方法;
2.能用HL证明三角形中的边或角相等.
如图,给定直角三角形ABC (Rt△ABC),在透明纸上用直尺和圆规作△A'B'C′,使∠C'为直角,A'C'=AC,A'B'=AB.
B
C
A
作法:
1.作∠PC′Q=90° .
2.在射线C′P上截取A′C′=AC.
3.作A′B′=AB,交射线CQ'于点B'.
Rt△A'B′C′即为所求.
Q
C′
P
A′
B′
作出的△A′B′C′ 和△ABC全等吗?为什么?
B
C
A
C′
B′
A′
P
Q
如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°AB=A′B′,AC=A′C′.
将△ABC和△A′B′C′分别沿BC和B′C′翻折,得到△ABP和△A'B′Q.
在△ABP和△A'B′Q中,
?????????=????′????′,????????=????′????,????????=????′????,
∴△ABP≌△A'B′Q(SSS).
∴∠A=∠A'.
在Rt△ABC和Rt△A'B′C′中,
?????????=????′????′,∠????=∠????′,????????=????′????′,
∴Rt△ABC≌Rt△A'B′C′(SAS).
?
证明:
判定两个直角三角形全等的定理:斜边和一条直角边分别相等的两个直角三角形全等.简记成“HL”.
符号语言:在 Rt△ABC 与 Rt△A'B'C' 中,∠C=∠C′=90°,如果
AC = A'C'
AB = A'B'
那么 Rt△ABC ≌ Rt△A'B'C' ( HL )
B'
A'
C'
B
A
C
不要丢了
1.如图,要用“????????”判定????????△????????????和????????△????′????′????′ 全等的条件可以是( )
?
C
A.????????=????′????′,????????=????′????′
B.∠????=∠????′,????????=????′????′
C.????????=????′????′,????????=????′????′
D.∠????=∠????′,????????=????′????′
?
活学活用
证明: ∵∠BAC=∠CDB=90°,
AC=DB,
BC=CB .
在 Rt△BCD 和Rt△CBA中,
∴ Rt△BCD≌Rt△CBA (HL).
B
C
A
D
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
例1 如图,∠BAC=∠CDB=90°, AC﹦DB,求证:AB﹦DC.
∴△BAC,△CDB都是直角三角形.
∴ AB﹦DC.
例2 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
A
D
C
B
O
分析:
1. AO与BO,CO与DO分别属于哪两个三角形?
2.证△ACO≌△BDO已有哪些条件?还缺什么条件?
3. AC、BD还属于哪两个三角形?
证明:在△ABC 和△BAD 中,∠C=∠D=90°,
????????=?????????,????????=????????,
∴ Rt△ABC≌Rt△BAD (HL).
∴ AC=BD.
在△AOC 和△BOD 中,
∠????=∠????,∠????????????=∠????????????,?????????=????????,???
∴△AOC≌△BOD,
∴AO=BO,CO=DO.
?
A
D
C
B
O
例2 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°,
求证:AO=BO,CO=DO.
如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
E
D
A
C
B
F
证明:∵ AD,AF分别是△ABC和△ABE的高,
∴∠ADB=∠AFB=90°.
在Rt△ADC和Rt△AFE中, ????????=????????,????????=????????,?
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
在Rt△ADB和Rt△AFB中, ????????=????????,????????=????????,?
∴Rt△ADB≌Rt△AFB(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
?
活学活用
HL判定
条件
斜边+一条直角边(隐含条件:直角相等)
作图验证
应用
A
1.如图,????????⊥????????,????????⊥???????? ,????????=????????,能直接判断????????△????????????≌????????△???????????? 的理由是( )
A.???????? B.???????????? C.???????????? D.????????????
?
2.已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.求证:AB//DC.
A
B
C
D
O
证明:∵ AC⊥BD于点O,
∴∠AOB=∠DOC=90°,
∴△AOB和△COD都是直角三角形,
∵ OA=OC,AB=CD.
∴△AOB≌△COD(HL)
∴∠A=∠C
∴AB//DC.
A
F
C
E
D
B
3.如图,AB=CD ,BF⊥AC ,DE⊥AC ,AE=CF. 求证:BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,
AB=CD,
AF=CE.
∴ Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
∴∠BFA=∠DEC=90 °.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在Rt△ABF和Rt△CDE中,
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
