3.5找质数同步练习(含解析)北师大版数学五年级上册
文档属性
| 名称 | 3.5找质数同步练习(含解析)北师大版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 425.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 13:10:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.5找质数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面( )组数中的两个数都是质数。
A.1和2 B.9和11 C.13和31 D.49和51
2.19乘a是质数,则a是( )。
A.1 B.19 C.任一质数
3.一个合数为a,则a至少有( )因数。
A.一个 B.两个 C.三个 D.四个
4.将1-9的数字卡牌放入学具袋,任意抽出一张卡牌,抽中( )的可能性最大。
A.奇数 B.偶数 C.质数 D.合数
5.10以内所有质数的和是( )。
A.17 B.18 C.19
6.在所有的质数中,偶数的个数( )。
A.一个也没有 B.只有一个 C.有无数个
7.一个比1大的数除了1和它本身之外,没有其他的因数,这个数是( )。
A.质数 B.合数 C.奇数 D.偶数
8.一个三位数,个位上是最小的质数,十位上的数是个位上的数的3倍,百位上是最小的合数,这个三位数是( )。
A.264 B.254 C.432 D.462
9.20以内所有质数的和是( )。
A.76 B.77 C.78 D.80
10.下列说法正确的有( )个。
①所有的奇数都是质数。 ②两个相邻的非0自然数的和一定是合数。
③5的所有倍数都是合数。 ④奇数+奇数=偶数,奇数+偶数=奇数。
⑤奇数都不是2的倍数。 ⑥一个数的倍数一定大于它的因数。
A.2 B.3 C.4 D.5
二、填空题
11.2有( )个因数,它是( )(填“质”或“合”)数,也是( )(填“偶”或“奇”)数。
12.最小的质数是( ),最小的合数是( ),既是质数又是偶数的数是( ),既是质数又是奇数的最小数是( ),既不是质数又不是合数的是( )。
13.分一分,填一填,并与同伴交流你的想法。
1 10 12 25 37 54 102 417 23 298
14.2024年8月12日巴黎奥运会落下帷幕,中国队斩获40金,以91枚总奖牌排名奖牌榜第二名。阅读榜中所有包含数的相关信息(节选),再用其中的数填空。
国家 金牌 银牌 铜牌 合计
美国 40 44 42 126
中国 40 27 24 91
澳大利亚 18 19 16 45
(1)偶数有( ),奇数有( )。
(2)40的因数有( ),4的倍数有( )。
(3)找出一个与众不同的数是( ),它与众不同是因为( )。
15.在1—20中,既不是合数,也不是质数的是( );既是奇数,又是合数的是( );既是偶数,又是质数的是( )。
16.一个门禁密码是由5个数字ABCDE组成:A是最小的合数;B是5的最小倍数;C既是3的倍数,又是3的因数;D的所有因数是1、2、4、8;E既是质数又是偶数。这个门禁的密码是( )。
17.9有( )个因数,所以9是( )数(填“质”或“合”)。
18.陈景润“1+2”定理:一个偶数=一个质数+一个质数×一个质数,其中偶数必须充分大,请根据这个定理分一分下面的偶数。
19.中国女篮在2023年大运会决赛中战胜日本队夺冠。队员韩旭得18分,10篮板9助攻。比赛期间她穿的球衣号是比50小的两位数,是7的倍数。个位上的数字既不是质数也不是合数,她的球衣号码是( )。
20.一个合数至少有( )个因数。
三、判断题
21.13、81、47这3个数都是质数。( )
22.把合数减去1之后,都将变成质数。( )
23.除2外,其它质数中的任意两个的和都是偶数。( )
四、解答题
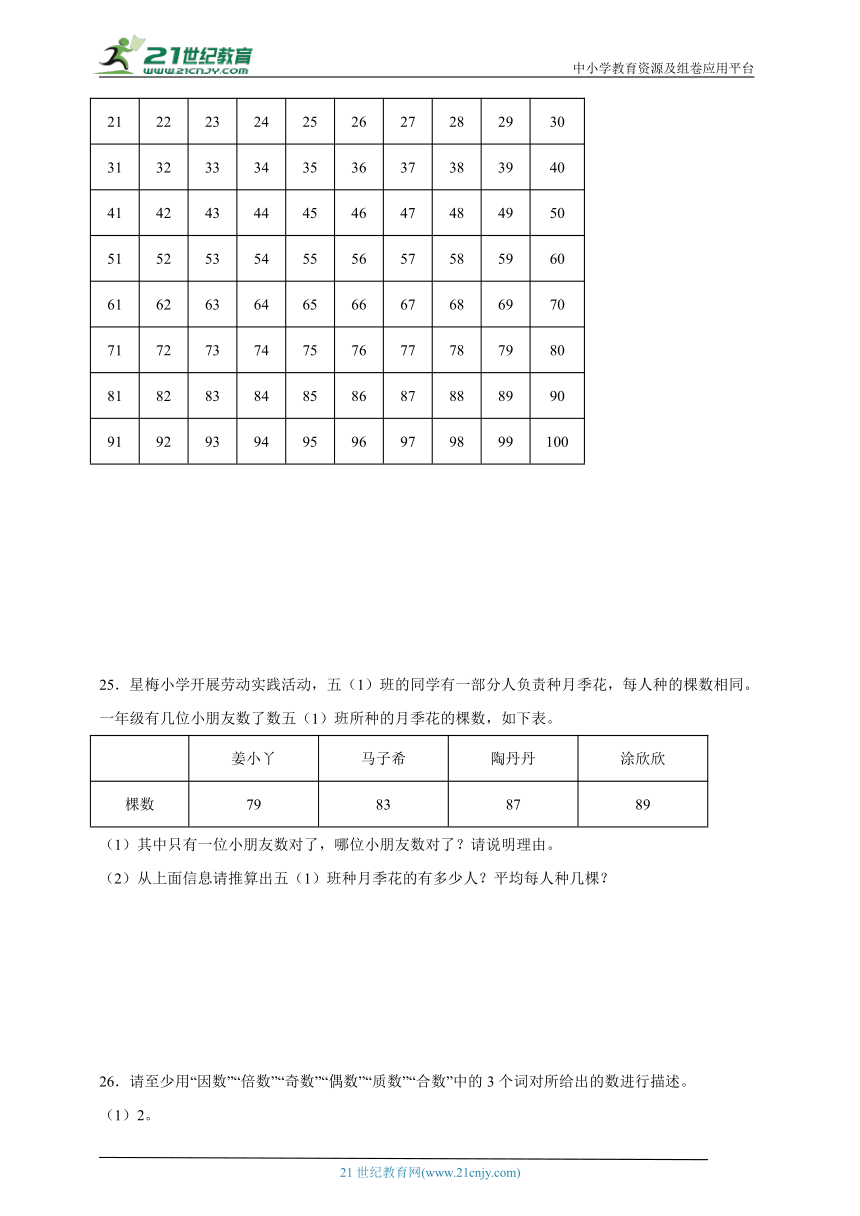
24.1~100中哪些数是质数?一位聪明的数学家想出了一个寻找质数的简单方法。在下面的百数表中:
①划掉1;
②划掉除2外所有2的倍数;
③划掉除3外所有3的倍数;
④划掉除5外所有5的倍数。
如此做下去,剩下的就是质数。
请在百数表中试着做一做,用彩色笔将质数圈起来。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
25.星梅小学开展劳动实践活动,五(1)班的同学有一部分人负责种月季花,每人种的棵数相同。一年级有几位小朋友数了数五(1)班所种的月季花的棵数,如下表。
姜小丫 马子希 陶丹丹 涂欣欣
棵数 79 83 87 89
(1)其中只有一位小朋友数对了,哪位小朋友数对了?请说明理由。
(2)从上面信息请推算出五(1)班种月季花的有多少人?平均每人种几棵?
26.请至少用“因数”“倍数”“奇数”“偶数”“质数”“合数”中的3个词对所给出的数进行描述。
(1)2。
(2)9。
27.小明家的门锁是个密码锁,已知这个密码锁的密码是一个6位数,第一位上的数是最小的质数;第二位上的数是最小合数的2倍;第三位上的数是3的倍数,且是最大的一位数;第四位上的数既是5的倍数又是5的因数;第五位上的数的所有因数是1,7;第六位上的数是第一位上数的3倍。这个密码锁的密码是多少?请写出你的理由。
28.茶叶店把84个小青柑装在不同的盒子里,每个盒子装的小青柑个数相同且为质数个,有几种不同的装法?每种装法各需要几个盒子?
《3.5找质数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C A A B A D B A
1.C
【分析】根据质数的意义:除了1和它本身,没有其它因数的数是质数;合数:除了1和它本身,还有其它因数的数是合数,1既不是质数也不是合数,据此即可逐项分析。
【详解】A.1既不是质数也不是合数;不符合题意;
B.9是合数,不符合题意;
C.13是质数,31也是质数,符合题意;
D.49是合数,51也是合数,不符合题意。
故答案为:C
【点睛】本题主要考查质数和合数的意义,熟练掌握它们的意义是解题的关键。
2.A
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,据此逐一分析即可。
【详解】由分析可得:
A.当a=1时,19×a=19×1=19,19只有1和19两个因数,所以19是质数,即a=1时19乘a是质数;
B.当a=19时,19×a=19×19=361,361不是质数,所以a=19时19乘a不是质数,不符合题意;
C.当a=任一质数,可以假设当a=2时,19×a=19×2=38,38不是质数,所以a=19时19乘a不是质数,不符合题意;
故答案为:A
【点睛】本题考查的是质数的有关知识,需要熟练掌握质数的概念,同时牢记常用的质数有哪些是解题的关键。
3.C
【分析】合数是指就除了1和它本身的两个因数以外还有其他的因数的数。据此解答。
【详解】根据合数的意义可知,一个合数为a,则a至少有三个因数。
故答案为:C
【点睛】此题主要考查合数的概念及意义。
4.A
【分析】奇数:不能被2整除的数,偶数:能被2整除的数,质数:除了1和它本身没有别的因数的数,合数:除了1和它本身还有别的因数的数;据此分别确定1-9中的奇数、偶数、质数、合数的个数,再根据哪种类型的卡牌最多,则抽中的可能性最大解答即可。
【详解】奇数:1,3,5,7,9,有5个;
偶数:2,4,6,8,有4个;
质数:2,3,5,7,有4个;
合数:4,6,8,9,有4个;
5>4,1-9中奇数最多。
将1-9的数字卡牌放入学具袋,任意抽出一张卡牌,抽中奇数的可能性最大。
故答案为:A
5.A
【分析】根据质数的意义:质数是指除了1和它本身的两个因数以外没有其他因数的数;找出10以内的质数,再相加,即可解答。
【详解】10以内的质数有:2、3、5、7。
2+3+5+7
=5+5+7
=10+7
=17
10以内所有质数的和是17。
故答案为:A
【点睛】本题考查质数的意义。
6.B
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,除了2以外,所有的质数都是奇数,据此答题即可。
【详解】由分析可得:
所有的质数中,只有一个偶数,就是2。
故答案为:B
【点睛】本题考查的是质数的有关知识,需要熟练掌握质数的概念,2是一个特殊的质数,经常会作为考点。
7.A
【详解】根据质数和合数的概念:除了1和它本身以外,不含其它因数的数是质数;除了1和它本身外,还含有其它因数的数是合数;据此解答即可。由次可知:一个比1大的数除了1和它本身之外,没有其他的因数,这个数是质数;
故答案为:A
8.D
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【详解】一个三位数,个位上是最小的质数,即2;
十位上的数是个位上的数的3倍,即2×3=6;
百位上是最小的合数,即4;
这个三位数是462。
故答案为:D
9.B
【分析】质数是指除了1和它本身的两个因数以外,再没有其他的因数,这样的数叫做质数;据此找出20以内的质数,即可解答。
【详解】20以内的质数有:2,3,5,7,11,13,17,19。
2+3+5+7+11+13+17+19=77
20以内所有质数的和是77。
故答案为:B
【点睛】熟练掌握质数的意义是解答本题的关键。
10.A
【分析】根据奇数与偶数定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据质数和合数的定义:一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数;一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数;根据运算性质:偶数+偶数=偶数;奇数+奇数=偶数;偶数+奇数=奇数;据此逐项进行判断。
【详解】①1是奇数,但1既不是质数也不是合数,因此不是所有的奇数都是质数,该说法是错误的。
②取两个相邻的非0自然数为:1和2,1+2=3,其中3是质数,因此两个相邻的非0自然数的和不一定是合数,该说法是错误的。
③5的倍数有:5,10,15,20,…,其中5是质数不是合数,因此该说法是错误的。
④根据运算性质:奇数+奇数=偶数,奇数+偶数=奇数,该说法是正确的。
⑤根据奇数的定义:不是2的倍数的数是奇数,因此该说法是正确的。
⑥一个数的最大的因数是它本身,一个数的最小的倍数是它本身,因此一个数的倍数也可以等于它的因数,该说法是错误的。
因此说法正确的有:④⑤,一共有2个。
故答案为:A
11. 2 质 偶
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。
只有1和它本身两个因数的数叫做质数;除了1和它本身,还有其它因数的数叫做合数。
不能被2整除的数叫做奇数,奇数的个位上是1,3,5,7或9;能被2整除的数叫做偶数,偶数个位上的数是0,2,4,6或8。据此解答。
【详解】2=1×2,则2的因数有1,2,共2个因数;2是质数,也是偶数。
12. 2 4 2 3 1
【分析】根据奇数与偶数定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据质数和合数的定义:一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数;一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数;据解答。
【详解】1既不是质数也不是合数,质数有:2,3,5,7,…,最小的质数是2;
合数有:4,6,8,9,10,…,最小的合数是4;
偶数有:0,2,4,6,8,…,既是质数又是偶数的数是2;
奇数有:1,3,5,7,9,…,既是质数又是奇数的数有:3,5,7,11,…
因此最小的质数是2;最小的合数是4;既是质数又是偶数的数是2;既是质数又是奇数的最小数是3;既不是质数又不是合数的是1。
13.
【分析】整数中,不能被2整除的数是奇数,能被2整除的数是偶数;质数:就是在所有比1大的整数中,除了1和它本身以外,不再有别的因数,这种整数叫做质数,合数是除了1和它本身还有其他因数,据此判断即可。。
【详解】奇数:个位上是1、3、5、7、9的数;
偶数:个位上是0、2、4、6、8的数;
1既不是质数也不是合数;
质数:只有1和它本身两个因数;
合数:除了1和它本身,还有其他因数;
据此把这些数填入各自的集合圈中。
【点睛】本题考查奇数与偶数、质数与合数,解答本题的关键是掌握奇数与偶数、质数与合数的特征。
14.(1) 40、44、42、126、24、18、16 27、91、19、45
(2) 40 40、44、24、16
(3) 19 它既是奇数又是质数
【分析】(1)整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
(2)找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
找一个数的倍数的方法:列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
(3)从这些数中找出一个与众不同的数,写出理由,合理即可。
【详解】(1)偶数有(40、44、42、126、24、18、16),奇数有(27、91、19、45)。
(2)40=1×40=2×20=4×10=5×8
40的因数有(40),4的倍数有(40、44、24、16)。
(3)找出一个与众不同的数是(19),它与众不同是因为(它既是奇数又是质数)。
(答案不唯一)
15. 1 9、15 2
【分析】
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
【详解】在1—20中,既不是合数,也不是质数的是1;既是奇数,又是合数的是9、15;既是偶数,又是质数的是2。
16.45382
【分析】最小的合数是4,则A是4;一个数的最小倍数是它本身,B是5的最小倍数,则B是5;C既是3的倍数,又是3的因数,则C是3;一个数的最大因数是它本身,D的所有因数是1、2、4、8,则D是8;E既是质数又是偶数,则E是2;据此解答即可。
【详解】由分析可知:这个门禁的密码是45382。
17. 3 合
【分析】根据一个数只有1和它本身两个因数,这个数叫作质数。一个数除了1和它本身以外还有别的因数,这个数叫作合数。1既不是质数,也不是合数。找出9的所有因数,从最小的自然数1找起,一直找到它本身,一对对找,即可解答。
【详解】9=1×9=3×3
9的因数有1、3、9,共3个,所以9是合数。
18.20=5+3×5
30=5+5×5
40=19+3×7或40=7+3×11
【分析】质数:只有1和它本身这两个因数的数是质数;奇数+奇数=偶数,偶数+偶数=偶数,据此填写即可。
【详解】由分析可知:
20=5+3×5
30=5+5×5
40=19+3×7或40=7+3×11
【点睛】本题考查质数的应用;注意:只有1和它本身这两个因数的数是质数。
19.21
【分析】根据题意,先列举出50以内7的倍数,再结合“个位上的数字既不是质数也不是合数”,那么这个两位数的个位上是1,由此确定她的球衣号码。
【详解】50以内7的倍数:7,14,21,28,35,42,49;
且个位上的数字既不是质数也不是合数,那么这个两位数的个位是1;
50以内7的倍数中只有21的个位是1,所以她的球衣号码是21。
20.3
【分析】一个大于1的自然数,除了1和它自身外,还能整除其他自然数的数,即除了1和它本身以外还有其他因数,这样的数叫合数。通过对合数概念的理解答题即可。
【详解】由分析可得:
合数至少有3个因数,比如4有因数1、2、4,所以4是合数;9有因数1、3、9,所以9是合数。
综上所述:一个合数至少有3个因数。
【点睛】本题考查了合数的概念,要求学生不能光死记硬背概念,而是要把对概念的理解,熟练的运用到题目中来。
21.×
【分析】一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数,据此判断即可。
【详解】由分析可知:
13和47是质数,81是合数,所以原题干说法错误。
故答案为:×
【点睛】本题考查质数和合数,明确它们的定义是解题的关键。
22.×
【分析】一个大于1的自然数,除了1和它自身外,还能整除其他自然数的数,即除了1和它本身以外还有其他因数,这样的数叫合数。在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,通过对合数和质数概念的理解和分析对此题进行判断即可。
【详解】由分析可得:
合数至少有3个因数,比如4有因数1、2、4,所以4是合数;9有因数1、3、9,所以9是合数。
9-1=8,8有因数1、2、4、8,8是合数,不是质数。
所以把合数减去1之后,并不一定都将变成质数。
故答案为:×
【点睛】本题考查了合数和质数的概念,要求学生不能光死记硬背概念,而是要把对概念的理解,熟练的运用到题目中来。
23.√
【分析】根据题意,除2以外的质数都是奇数,根据奇数+奇数=偶数,据此判断即可。
【详解】由分析可知:
除2外,其它质数中的任意两个的和都是偶数。说法正确。
故答案为:√
【点睛】此题考查的是质数和奇数的含义,明确质数中除了2之外,所有的质数都为奇数是解题关键。
24.见详解
【分析】百数表中,除2外所有2的倍数有4、6、8、10、12、14、16、18、20、22、24、26、28、30、32、34、36、38、40、42、44、46、48、50、52、54、56、58、60、62、64、66、68、70、72、74、76、78、80、82、84、86、88、90、92、94、96、98和100;
百数表中,划掉除3外所有3的倍数有6、9、12、15、18、21、24、27、30、33、36、39、42、45、48、51、54、57、60、63、66、69、72、75、78、81、84、87、90、93、96和99;
百数表中,划掉除5外所有5的倍数有10、15、20、25、30、35、40、45、50、55、60、65、70、75、80、85、90、95和100。
……
特别要注意的是百数表中的49,因为49=7×7,所以49不是质数,也要划掉。
【详解】
25.(1)陶丹丹数对了;理由见详解
(2))29人;3棵
【分析】(1)除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。因为总棵数=每人种的棵数×人数,总棵数的因数除了1和本身,还有每人种的棵数和人数,根据实际情况,总棵数应该是合数,据此分析。
(2)列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。据此求出总棵数的所有因数,根据总棵数=每人种的棵数×人数,结合实际情况确定人数和每人种的棵数。
【详解】(1)陶丹丹数对了;因为79、83、89都是质数,只有1和本身两个因数。要么每人只种一棵,那么人数就不符合实际人数。如果只有一个同学种,那么和有些同学负责种月季花不符合。所以只有87棵是对的。
(2)87=1×87=3×29
根据实际情况3和29是人数和每人种的棵数。
答:五(1)班种月季花的有29人,平均每人种3棵或有3人,平均每人种29棵。
26.见详解
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。
整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】(1)2是偶数中唯一的质数,2的因数只有1和它本身。
(2)9是奇数,也是合数,9的最小倍数是9。
27.289576;理由见详解
【分析】质数:一个数,只有1和它本身两个因数,这样的数叫做质数;最小的质数是2;
合数:一个数,除了1和它本数两个因数外,还有其他因数,这样的数叫做合数,最小的合数是4;一个数,最小的倍数和最大的因数是它本身;以及求一个数倍数的方法进行解答。
【详解】第一位:最小的质数是2,是2;
第二位:最小的合数是4;4×2=8,是8;
第三位:是3的倍数,且是最大的一位数,是9;
第四位:5既是5的倍数,也是5的因数,是5;
第五位:所有因数是1,7,1×7=7,是7;
第六位:是第一位上数的3倍,2×3=6,是6。
这个密码锁是289576。
答:这个密码锁是289576。
28.3种;每盒装2个,需要42个盒子,每盒装3个,需要28个盒子,每盒装7个,需要12个盒子。
【分析】首先对84分解质因数,得到84=2×2×3×7,有几个不同的质因数就有几种不同的装法;题目要求每个盒子装同样多小青柑且为质数个,所以可以将2、3、7看作小青柑的数量,用总个数分别除以每盒装的个数,可得需要几个盒子。
【详解】由分析可得:
84=2×2×3×7,分别有2、3、7三种不同质因数,所以有3种不同装法;
84÷2=42(个)
84÷3=28(个)
84÷7=12(个)
答:有3种不同的装法。每盒装2个,需要42个盒子,每盒装3个,需要28个盒子,每盒装7个,需要12个盒子。
【点睛】本题考查了分解质因数的灵活运用,解题的关键是明确分解出来的质因数就是每个盒子装的小青柑的个数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.5找质数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面( )组数中的两个数都是质数。
A.1和2 B.9和11 C.13和31 D.49和51
2.19乘a是质数,则a是( )。
A.1 B.19 C.任一质数
3.一个合数为a,则a至少有( )因数。
A.一个 B.两个 C.三个 D.四个
4.将1-9的数字卡牌放入学具袋,任意抽出一张卡牌,抽中( )的可能性最大。
A.奇数 B.偶数 C.质数 D.合数
5.10以内所有质数的和是( )。
A.17 B.18 C.19
6.在所有的质数中,偶数的个数( )。
A.一个也没有 B.只有一个 C.有无数个
7.一个比1大的数除了1和它本身之外,没有其他的因数,这个数是( )。
A.质数 B.合数 C.奇数 D.偶数
8.一个三位数,个位上是最小的质数,十位上的数是个位上的数的3倍,百位上是最小的合数,这个三位数是( )。
A.264 B.254 C.432 D.462
9.20以内所有质数的和是( )。
A.76 B.77 C.78 D.80
10.下列说法正确的有( )个。
①所有的奇数都是质数。 ②两个相邻的非0自然数的和一定是合数。
③5的所有倍数都是合数。 ④奇数+奇数=偶数,奇数+偶数=奇数。
⑤奇数都不是2的倍数。 ⑥一个数的倍数一定大于它的因数。
A.2 B.3 C.4 D.5
二、填空题
11.2有( )个因数,它是( )(填“质”或“合”)数,也是( )(填“偶”或“奇”)数。
12.最小的质数是( ),最小的合数是( ),既是质数又是偶数的数是( ),既是质数又是奇数的最小数是( ),既不是质数又不是合数的是( )。
13.分一分,填一填,并与同伴交流你的想法。
1 10 12 25 37 54 102 417 23 298
14.2024年8月12日巴黎奥运会落下帷幕,中国队斩获40金,以91枚总奖牌排名奖牌榜第二名。阅读榜中所有包含数的相关信息(节选),再用其中的数填空。
国家 金牌 银牌 铜牌 合计
美国 40 44 42 126
中国 40 27 24 91
澳大利亚 18 19 16 45
(1)偶数有( ),奇数有( )。
(2)40的因数有( ),4的倍数有( )。
(3)找出一个与众不同的数是( ),它与众不同是因为( )。
15.在1—20中,既不是合数,也不是质数的是( );既是奇数,又是合数的是( );既是偶数,又是质数的是( )。
16.一个门禁密码是由5个数字ABCDE组成:A是最小的合数;B是5的最小倍数;C既是3的倍数,又是3的因数;D的所有因数是1、2、4、8;E既是质数又是偶数。这个门禁的密码是( )。
17.9有( )个因数,所以9是( )数(填“质”或“合”)。
18.陈景润“1+2”定理:一个偶数=一个质数+一个质数×一个质数,其中偶数必须充分大,请根据这个定理分一分下面的偶数。
19.中国女篮在2023年大运会决赛中战胜日本队夺冠。队员韩旭得18分,10篮板9助攻。比赛期间她穿的球衣号是比50小的两位数,是7的倍数。个位上的数字既不是质数也不是合数,她的球衣号码是( )。
20.一个合数至少有( )个因数。
三、判断题
21.13、81、47这3个数都是质数。( )
22.把合数减去1之后,都将变成质数。( )
23.除2外,其它质数中的任意两个的和都是偶数。( )
四、解答题
24.1~100中哪些数是质数?一位聪明的数学家想出了一个寻找质数的简单方法。在下面的百数表中:
①划掉1;
②划掉除2外所有2的倍数;
③划掉除3外所有3的倍数;
④划掉除5外所有5的倍数。
如此做下去,剩下的就是质数。
请在百数表中试着做一做,用彩色笔将质数圈起来。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
25.星梅小学开展劳动实践活动,五(1)班的同学有一部分人负责种月季花,每人种的棵数相同。一年级有几位小朋友数了数五(1)班所种的月季花的棵数,如下表。
姜小丫 马子希 陶丹丹 涂欣欣
棵数 79 83 87 89
(1)其中只有一位小朋友数对了,哪位小朋友数对了?请说明理由。
(2)从上面信息请推算出五(1)班种月季花的有多少人?平均每人种几棵?
26.请至少用“因数”“倍数”“奇数”“偶数”“质数”“合数”中的3个词对所给出的数进行描述。
(1)2。
(2)9。
27.小明家的门锁是个密码锁,已知这个密码锁的密码是一个6位数,第一位上的数是最小的质数;第二位上的数是最小合数的2倍;第三位上的数是3的倍数,且是最大的一位数;第四位上的数既是5的倍数又是5的因数;第五位上的数的所有因数是1,7;第六位上的数是第一位上数的3倍。这个密码锁的密码是多少?请写出你的理由。
28.茶叶店把84个小青柑装在不同的盒子里,每个盒子装的小青柑个数相同且为质数个,有几种不同的装法?每种装法各需要几个盒子?
《3.5找质数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C A A B A D B A
1.C
【分析】根据质数的意义:除了1和它本身,没有其它因数的数是质数;合数:除了1和它本身,还有其它因数的数是合数,1既不是质数也不是合数,据此即可逐项分析。
【详解】A.1既不是质数也不是合数;不符合题意;
B.9是合数,不符合题意;
C.13是质数,31也是质数,符合题意;
D.49是合数,51也是合数,不符合题意。
故答案为:C
【点睛】本题主要考查质数和合数的意义,熟练掌握它们的意义是解题的关键。
2.A
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,据此逐一分析即可。
【详解】由分析可得:
A.当a=1时,19×a=19×1=19,19只有1和19两个因数,所以19是质数,即a=1时19乘a是质数;
B.当a=19时,19×a=19×19=361,361不是质数,所以a=19时19乘a不是质数,不符合题意;
C.当a=任一质数,可以假设当a=2时,19×a=19×2=38,38不是质数,所以a=19时19乘a不是质数,不符合题意;
故答案为:A
【点睛】本题考查的是质数的有关知识,需要熟练掌握质数的概念,同时牢记常用的质数有哪些是解题的关键。
3.C
【分析】合数是指就除了1和它本身的两个因数以外还有其他的因数的数。据此解答。
【详解】根据合数的意义可知,一个合数为a,则a至少有三个因数。
故答案为:C
【点睛】此题主要考查合数的概念及意义。
4.A
【分析】奇数:不能被2整除的数,偶数:能被2整除的数,质数:除了1和它本身没有别的因数的数,合数:除了1和它本身还有别的因数的数;据此分别确定1-9中的奇数、偶数、质数、合数的个数,再根据哪种类型的卡牌最多,则抽中的可能性最大解答即可。
【详解】奇数:1,3,5,7,9,有5个;
偶数:2,4,6,8,有4个;
质数:2,3,5,7,有4个;
合数:4,6,8,9,有4个;
5>4,1-9中奇数最多。
将1-9的数字卡牌放入学具袋,任意抽出一张卡牌,抽中奇数的可能性最大。
故答案为:A
5.A
【分析】根据质数的意义:质数是指除了1和它本身的两个因数以外没有其他因数的数;找出10以内的质数,再相加,即可解答。
【详解】10以内的质数有:2、3、5、7。
2+3+5+7
=5+5+7
=10+7
=17
10以内所有质数的和是17。
故答案为:A
【点睛】本题考查质数的意义。
6.B
【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,除了2以外,所有的质数都是奇数,据此答题即可。
【详解】由分析可得:
所有的质数中,只有一个偶数,就是2。
故答案为:B
【点睛】本题考查的是质数的有关知识,需要熟练掌握质数的概念,2是一个特殊的质数,经常会作为考点。
7.A
【详解】根据质数和合数的概念:除了1和它本身以外,不含其它因数的数是质数;除了1和它本身外,还含有其它因数的数是合数;据此解答即可。由次可知:一个比1大的数除了1和它本身之外,没有其他的因数,这个数是质数;
故答案为:A
8.D
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【详解】一个三位数,个位上是最小的质数,即2;
十位上的数是个位上的数的3倍,即2×3=6;
百位上是最小的合数,即4;
这个三位数是462。
故答案为:D
9.B
【分析】质数是指除了1和它本身的两个因数以外,再没有其他的因数,这样的数叫做质数;据此找出20以内的质数,即可解答。
【详解】20以内的质数有:2,3,5,7,11,13,17,19。
2+3+5+7+11+13+17+19=77
20以内所有质数的和是77。
故答案为:B
【点睛】熟练掌握质数的意义是解答本题的关键。
10.A
【分析】根据奇数与偶数定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据质数和合数的定义:一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数;一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数;根据运算性质:偶数+偶数=偶数;奇数+奇数=偶数;偶数+奇数=奇数;据此逐项进行判断。
【详解】①1是奇数,但1既不是质数也不是合数,因此不是所有的奇数都是质数,该说法是错误的。
②取两个相邻的非0自然数为:1和2,1+2=3,其中3是质数,因此两个相邻的非0自然数的和不一定是合数,该说法是错误的。
③5的倍数有:5,10,15,20,…,其中5是质数不是合数,因此该说法是错误的。
④根据运算性质:奇数+奇数=偶数,奇数+偶数=奇数,该说法是正确的。
⑤根据奇数的定义:不是2的倍数的数是奇数,因此该说法是正确的。
⑥一个数的最大的因数是它本身,一个数的最小的倍数是它本身,因此一个数的倍数也可以等于它的因数,该说法是错误的。
因此说法正确的有:④⑤,一共有2个。
故答案为:A
11. 2 质 偶
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。
只有1和它本身两个因数的数叫做质数;除了1和它本身,还有其它因数的数叫做合数。
不能被2整除的数叫做奇数,奇数的个位上是1,3,5,7或9;能被2整除的数叫做偶数,偶数个位上的数是0,2,4,6或8。据此解答。
【详解】2=1×2,则2的因数有1,2,共2个因数;2是质数,也是偶数。
12. 2 4 2 3 1
【分析】根据奇数与偶数定义:是2的倍数的数叫偶数,不是2的倍数的数叫奇数;根据质数和合数的定义:一个大于1的自然数,除了1和它本身以外不再有其他因数,这样的数叫质数;一个大于1的自然数,除了1和它本身以外还有其他因数,这样的数叫合数;据解答。
【详解】1既不是质数也不是合数,质数有:2,3,5,7,…,最小的质数是2;
合数有:4,6,8,9,10,…,最小的合数是4;
偶数有:0,2,4,6,8,…,既是质数又是偶数的数是2;
奇数有:1,3,5,7,9,…,既是质数又是奇数的数有:3,5,7,11,…
因此最小的质数是2;最小的合数是4;既是质数又是偶数的数是2;既是质数又是奇数的最小数是3;既不是质数又不是合数的是1。
13.
【分析】整数中,不能被2整除的数是奇数,能被2整除的数是偶数;质数:就是在所有比1大的整数中,除了1和它本身以外,不再有别的因数,这种整数叫做质数,合数是除了1和它本身还有其他因数,据此判断即可。。
【详解】奇数:个位上是1、3、5、7、9的数;
偶数:个位上是0、2、4、6、8的数;
1既不是质数也不是合数;
质数:只有1和它本身两个因数;
合数:除了1和它本身,还有其他因数;
据此把这些数填入各自的集合圈中。
【点睛】本题考查奇数与偶数、质数与合数,解答本题的关键是掌握奇数与偶数、质数与合数的特征。
14.(1) 40、44、42、126、24、18、16 27、91、19、45
(2) 40 40、44、24、16
(3) 19 它既是奇数又是质数
【分析】(1)整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
(2)找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
找一个数的倍数的方法:列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。
(3)从这些数中找出一个与众不同的数,写出理由,合理即可。
【详解】(1)偶数有(40、44、42、126、24、18、16),奇数有(27、91、19、45)。
(2)40=1×40=2×20=4×10=5×8
40的因数有(40),4的倍数有(40、44、24、16)。
(3)找出一个与众不同的数是(19),它与众不同是因为(它既是奇数又是质数)。
(答案不唯一)
15. 1 9、15 2
【分析】
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
【详解】在1—20中,既不是合数,也不是质数的是1;既是奇数,又是合数的是9、15;既是偶数,又是质数的是2。
16.45382
【分析】最小的合数是4,则A是4;一个数的最小倍数是它本身,B是5的最小倍数,则B是5;C既是3的倍数,又是3的因数,则C是3;一个数的最大因数是它本身,D的所有因数是1、2、4、8,则D是8;E既是质数又是偶数,则E是2;据此解答即可。
【详解】由分析可知:这个门禁的密码是45382。
17. 3 合
【分析】根据一个数只有1和它本身两个因数,这个数叫作质数。一个数除了1和它本身以外还有别的因数,这个数叫作合数。1既不是质数,也不是合数。找出9的所有因数,从最小的自然数1找起,一直找到它本身,一对对找,即可解答。
【详解】9=1×9=3×3
9的因数有1、3、9,共3个,所以9是合数。
18.20=5+3×5
30=5+5×5
40=19+3×7或40=7+3×11
【分析】质数:只有1和它本身这两个因数的数是质数;奇数+奇数=偶数,偶数+偶数=偶数,据此填写即可。
【详解】由分析可知:
20=5+3×5
30=5+5×5
40=19+3×7或40=7+3×11
【点睛】本题考查质数的应用;注意:只有1和它本身这两个因数的数是质数。
19.21
【分析】根据题意,先列举出50以内7的倍数,再结合“个位上的数字既不是质数也不是合数”,那么这个两位数的个位上是1,由此确定她的球衣号码。
【详解】50以内7的倍数:7,14,21,28,35,42,49;
且个位上的数字既不是质数也不是合数,那么这个两位数的个位是1;
50以内7的倍数中只有21的个位是1,所以她的球衣号码是21。
20.3
【分析】一个大于1的自然数,除了1和它自身外,还能整除其他自然数的数,即除了1和它本身以外还有其他因数,这样的数叫合数。通过对合数概念的理解答题即可。
【详解】由分析可得:
合数至少有3个因数,比如4有因数1、2、4,所以4是合数;9有因数1、3、9,所以9是合数。
综上所述:一个合数至少有3个因数。
【点睛】本题考查了合数的概念,要求学生不能光死记硬背概念,而是要把对概念的理解,熟练的运用到题目中来。
21.×
【分析】一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数,据此判断即可。
【详解】由分析可知:
13和47是质数,81是合数,所以原题干说法错误。
故答案为:×
【点睛】本题考查质数和合数,明确它们的定义是解题的关键。
22.×
【分析】一个大于1的自然数,除了1和它自身外,还能整除其他自然数的数,即除了1和它本身以外还有其他因数,这样的数叫合数。在自然数中,除了1和它本身外,没有别的因数的数为质数,比如3,只有1和它本身这两个因数,所以3是质数,通过对合数和质数概念的理解和分析对此题进行判断即可。
【详解】由分析可得:
合数至少有3个因数,比如4有因数1、2、4,所以4是合数;9有因数1、3、9,所以9是合数。
9-1=8,8有因数1、2、4、8,8是合数,不是质数。
所以把合数减去1之后,并不一定都将变成质数。
故答案为:×
【点睛】本题考查了合数和质数的概念,要求学生不能光死记硬背概念,而是要把对概念的理解,熟练的运用到题目中来。
23.√
【分析】根据题意,除2以外的质数都是奇数,根据奇数+奇数=偶数,据此判断即可。
【详解】由分析可知:
除2外,其它质数中的任意两个的和都是偶数。说法正确。
故答案为:√
【点睛】此题考查的是质数和奇数的含义,明确质数中除了2之外,所有的质数都为奇数是解题关键。
24.见详解
【分析】百数表中,除2外所有2的倍数有4、6、8、10、12、14、16、18、20、22、24、26、28、30、32、34、36、38、40、42、44、46、48、50、52、54、56、58、60、62、64、66、68、70、72、74、76、78、80、82、84、86、88、90、92、94、96、98和100;
百数表中,划掉除3外所有3的倍数有6、9、12、15、18、21、24、27、30、33、36、39、42、45、48、51、54、57、60、63、66、69、72、75、78、81、84、87、90、93、96和99;
百数表中,划掉除5外所有5的倍数有10、15、20、25、30、35、40、45、50、55、60、65、70、75、80、85、90、95和100。
……
特别要注意的是百数表中的49,因为49=7×7,所以49不是质数,也要划掉。
【详解】
25.(1)陶丹丹数对了;理由见详解
(2))29人;3棵
【分析】(1)除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。因为总棵数=每人种的棵数×人数,总棵数的因数除了1和本身,还有每人种的棵数和人数,根据实际情况,总棵数应该是合数,据此分析。
(2)列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。据此求出总棵数的所有因数,根据总棵数=每人种的棵数×人数,结合实际情况确定人数和每人种的棵数。
【详解】(1)陶丹丹数对了;因为79、83、89都是质数,只有1和本身两个因数。要么每人只种一棵,那么人数就不符合实际人数。如果只有一个同学种,那么和有些同学负责种月季花不符合。所以只有87棵是对的。
(2)87=1×87=3×29
根据实际情况3和29是人数和每人种的棵数。
答:五(1)班种月季花的有29人,平均每人种3棵或有3人,平均每人种29棵。
26.见详解
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。
整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。
【详解】(1)2是偶数中唯一的质数,2的因数只有1和它本身。
(2)9是奇数,也是合数,9的最小倍数是9。
27.289576;理由见详解
【分析】质数:一个数,只有1和它本身两个因数,这样的数叫做质数;最小的质数是2;
合数:一个数,除了1和它本数两个因数外,还有其他因数,这样的数叫做合数,最小的合数是4;一个数,最小的倍数和最大的因数是它本身;以及求一个数倍数的方法进行解答。
【详解】第一位:最小的质数是2,是2;
第二位:最小的合数是4;4×2=8,是8;
第三位:是3的倍数,且是最大的一位数,是9;
第四位:5既是5的倍数,也是5的因数,是5;
第五位:所有因数是1,7,1×7=7,是7;
第六位:是第一位上数的3倍,2×3=6,是6。
这个密码锁是289576。
答:这个密码锁是289576。
28.3种;每盒装2个,需要42个盒子,每盒装3个,需要28个盒子,每盒装7个,需要12个盒子。
【分析】首先对84分解质因数,得到84=2×2×3×7,有几个不同的质因数就有几种不同的装法;题目要求每个盒子装同样多小青柑且为质数个,所以可以将2、3、7看作小青柑的数量,用总个数分别除以每盒装的个数,可得需要几个盒子。
【详解】由分析可得:
84=2×2×3×7,分别有2、3、7三种不同质因数,所以有3种不同装法;
84÷2=42(个)
84÷3=28(个)
84÷7=12(个)
答:有3种不同的装法。每盒装2个,需要42个盒子,每盒装3个,需要28个盒子,每盒装7个,需要12个盒子。
【点睛】本题考查了分解质因数的灵活运用,解题的关键是明确分解出来的质因数就是每个盒子装的小青柑的个数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
