13.2命题与证明 同步练习(含答案)
文档属性
| 名称 | 13.2命题与证明 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 400.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 11:46:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.2 命题与证明
一、单选题
1.下列命题错误的是( )
A.两个周长相等的三角形一定是全等三角形
B.全等三角形的对应角相等
C.全等三角形的面积相等
D.全等三角形的对应边相等
2.下列命题是假命题的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
3.下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的平行四边形是菱形
4.下列命题是真命题的是( )
①,,c是直线,若,,则.
②,,是直线,若,,则.
③若与互余,与互余,则与互余.
A.① B.①② C.②③ D.①②③
5.下列命题是真命题的是( )
A.同位角相等 B.内错角相等
C.同角的补角相等 D.相等的角是对顶角
二、填空题
6.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为 .
7.请将命题“邻补角互补”写成“如果……那么……”的形式: .
8."内错角相等,两直线平行"的逆命题是 ,该命题是 (填"真"或"假")命题。
9.将等腰直角三角板按如图的方式摆放,如果,那么 .
10.把命题“同角的补角相等”改成“如果... 那么....”的形式 .
11.写出命题“如果两个实数都是正数,那么它们的积是正数”的逆命题是
三、综合题
12.写出定理“等腰三角形顶角的角平分线和底边上的高线互相重合”的逆命题,并证明这个命题是真命题。
逆命题: 。
已知: 。
求证: 。
证明:
13.指出下列命题的题设和结论:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)相交的两条直线一定不平行.
14.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)对顶角相等;
(2)同角的余角相等;
(3)三角形的内角和等于180°;
(4)角平分线上的点到角的两边距离相等.
四、判断题
15.判断下列语句哪些是命题,哪些不是命题(填“正确”或“错误”).
(1)方程2x-4=0的解是x=2.( )
(2)这朵小花是红色的.( )
(3)在△ABC中,若AB>AC,则∠C>∠B吗 ( )
(4)若ab>0,则a>0.( )
(5)两个相等的同位角的角平分线平行.( )
(6)两个无理数的和必是无理数.( )
(7)请画出一对对顶角.( )
(8)(a为实数).( )
16.三角形的外角和等于与它相邻的两个内角的和
五、计算题
17.小明不小心将一块三角形玻璃(记)打破成三块(分别Ⅰ、Ⅱ、Ⅲ),如图所示,他在玻璃碎片Ⅱ上任取一点,连接、,度量得到=100°,°,°,根据以上数据,你能计算出原中哪个内角的度数,是多少度?说明理由.
18.(1)如图1,试探究与,,并说明理由.(请补充下面的证明过程)
解:连接并延长至点,如图2,由外角定理可得 ,,且,,相加可得 ;
(2)如图3,,分别平分,,它们交于点,,,请求出的度数.
六、解答题
19.如图,在中,是边上的高,平分,,,求的度数.
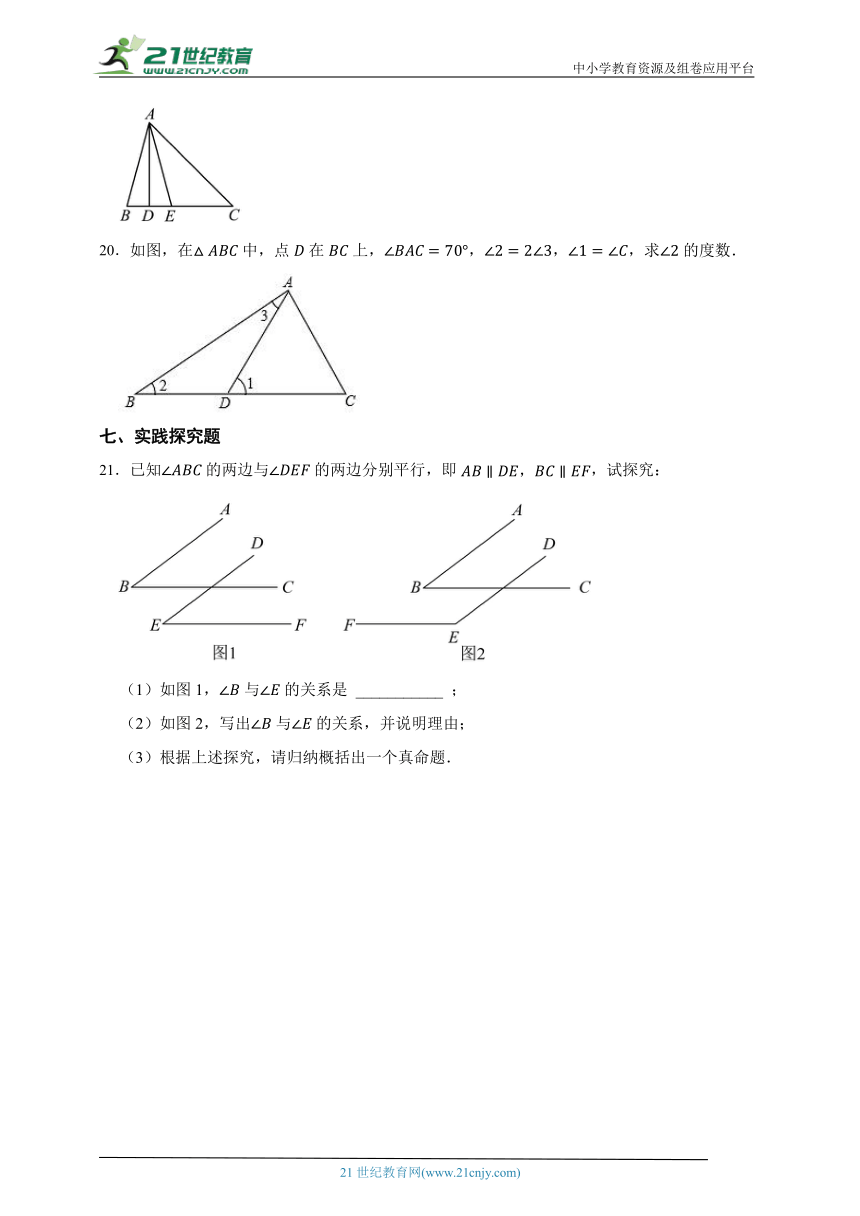
20.如图,在中,点在上,,,,求的度数.
七、实践探究题
21.已知的两边与的两边分别平行,即,试探究:
(1)如图1,与的关系是 ___________ ;
(2)如图2,写出与的关系,并说明理由;
(3)根据上述探究,请归纳概括出一个真命题.
答案解析部分
1.【答案】A
【知识点】真命题与假命题
2.【答案】B
【知识点】真命题与假命题;不等式的性质
3.【答案】C
【知识点】真命题与假命题
4.【答案】A
【知识点】余角、补角及其性质;平行公理及推论;平行线的判定;真命题与假命题
5.【答案】C
【知识点】余角、补角及其性质;平行线的性质;对顶角及其性质;真命题与假命题
6.【答案】145°
【知识点】三角形外角的概念及性质
7.【答案】如果两个角是邻补角,那么这两个角互补
【知识点】定义、命题、定理、推论的概念
8.【答案】两直线平行,内错角相等;真
【知识点】真命题与假命题;逆命题
9.【答案】150
【知识点】平行线的性质;三角形外角的概念及性质
10.【答案】如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题、定理、推论的概念
11.【答案】如果两个实数的积是正数,那么这两个数都是正数、
【知识点】逆命题
12.【答案】一边上的高线与这边对角的角平分线重合的三角形是等腰三角形;如图,AD⊥BC,AD是△ABC的角平分线 ;△ABC是等腰三角形。;∵AD是△ABC的角平分线, ∴∠BAD=∠CAD, 在△ADC和△ADB中, , ∴△ADC≌△ADB(AAS), ∴AB=AC, ∴△ABC是等腰三角形.
【知识点】真命题与假命题;逆命题
13.【答案】(1)解:题设是两条直线都与第三条直线平行,结论是这两条直线也互相平行
(2)解:“相交的两条直线一定不平行”可改写为“如果两条直线相交,那么它们一定不平行”,
故题设是两条直线相交,结论是它们一定不平行.
【知识点】定义、命题、定理、推论的概念
14.【答案】(1)解:如果两个角是对顶角,那么这两个角相等,
条件:两个角是对顶角,结论:这两个角相等
(2)解:如果两个角都是同一个角的余角,那么这两个角相等.
条件:两个角都是同一个角的余角,
结论:这两个角相等
(3)解:如果三个角是一个三角形的内角,那么这三个内角和等于180°.
条件:三个角是一个三角形的内角,
结论:这三个内角和等于180°
(4)解:如果一个点在角平分线上,那么它到角两边的距离相等.
条件:一个点在角平分线上,
结论:这个点到角两边的距离相等
【知识点】定义、命题、定理、推论的概念
15.【答案】(1)正确
(2)正确
(3)错误
(4)正确
(5)正确
(6)正确
(7)错误
(8)正确
【知识点】定义、命题、定理、推论的概念
16.【答案】错误
【知识点】三角形外角的概念及性质
17.【答案】可求出∠A=40°.
【知识点】三角形外角的概念及性质
18.【答案】(1); (2)
【知识点】三角形外角的概念及性质
19.【答案】
【知识点】三角形内角和定理;三角形外角的概念及性质
20.【答案】44°
【知识点】三角形内角和定理;三角形外角的概念及性质
21.【答案】(1)
(2)解:,理由如下:如下图,
∵,
∴,
又∵,
∴,
∴,
故答案为:;
(3)解:由题意得:如果两个角的两边分别平行,那么这两个角相等或者互补.
【知识点】平行线的性质;定义、命题、定理、推论的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.2 命题与证明
一、单选题
1.下列命题错误的是( )
A.两个周长相等的三角形一定是全等三角形
B.全等三角形的对应角相等
C.全等三角形的面积相等
D.全等三角形的对应边相等
2.下列命题是假命题的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
3.下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的平行四边形是菱形
4.下列命题是真命题的是( )
①,,c是直线,若,,则.
②,,是直线,若,,则.
③若与互余,与互余,则与互余.
A.① B.①② C.②③ D.①②③
5.下列命题是真命题的是( )
A.同位角相等 B.内错角相等
C.同角的补角相等 D.相等的角是对顶角
二、填空题
6.如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为 .
7.请将命题“邻补角互补”写成“如果……那么……”的形式: .
8."内错角相等,两直线平行"的逆命题是 ,该命题是 (填"真"或"假")命题。
9.将等腰直角三角板按如图的方式摆放,如果,那么 .
10.把命题“同角的补角相等”改成“如果... 那么....”的形式 .
11.写出命题“如果两个实数都是正数,那么它们的积是正数”的逆命题是
三、综合题
12.写出定理“等腰三角形顶角的角平分线和底边上的高线互相重合”的逆命题,并证明这个命题是真命题。
逆命题: 。
已知: 。
求证: 。
证明:
13.指出下列命题的题设和结论:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)相交的两条直线一定不平行.
14.指出下列命题的条件和结论,并改写成“如果……那么……”的形式:
(1)对顶角相等;
(2)同角的余角相等;
(3)三角形的内角和等于180°;
(4)角平分线上的点到角的两边距离相等.
四、判断题
15.判断下列语句哪些是命题,哪些不是命题(填“正确”或“错误”).
(1)方程2x-4=0的解是x=2.( )
(2)这朵小花是红色的.( )
(3)在△ABC中,若AB>AC,则∠C>∠B吗 ( )
(4)若ab>0,则a>0.( )
(5)两个相等的同位角的角平分线平行.( )
(6)两个无理数的和必是无理数.( )
(7)请画出一对对顶角.( )
(8)(a为实数).( )
16.三角形的外角和等于与它相邻的两个内角的和
五、计算题
17.小明不小心将一块三角形玻璃(记)打破成三块(分别Ⅰ、Ⅱ、Ⅲ),如图所示,他在玻璃碎片Ⅱ上任取一点,连接、,度量得到=100°,°,°,根据以上数据,你能计算出原中哪个内角的度数,是多少度?说明理由.
18.(1)如图1,试探究与,,并说明理由.(请补充下面的证明过程)
解:连接并延长至点,如图2,由外角定理可得 ,,且,,相加可得 ;
(2)如图3,,分别平分,,它们交于点,,,请求出的度数.
六、解答题
19.如图,在中,是边上的高,平分,,,求的度数.
20.如图,在中,点在上,,,,求的度数.
七、实践探究题
21.已知的两边与的两边分别平行,即,试探究:
(1)如图1,与的关系是 ___________ ;
(2)如图2,写出与的关系,并说明理由;
(3)根据上述探究,请归纳概括出一个真命题.
答案解析部分
1.【答案】A
【知识点】真命题与假命题
2.【答案】B
【知识点】真命题与假命题;不等式的性质
3.【答案】C
【知识点】真命题与假命题
4.【答案】A
【知识点】余角、补角及其性质;平行公理及推论;平行线的判定;真命题与假命题
5.【答案】C
【知识点】余角、补角及其性质;平行线的性质;对顶角及其性质;真命题与假命题
6.【答案】145°
【知识点】三角形外角的概念及性质
7.【答案】如果两个角是邻补角,那么这两个角互补
【知识点】定义、命题、定理、推论的概念
8.【答案】两直线平行,内错角相等;真
【知识点】真命题与假命题;逆命题
9.【答案】150
【知识点】平行线的性质;三角形外角的概念及性质
10.【答案】如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题、定理、推论的概念
11.【答案】如果两个实数的积是正数,那么这两个数都是正数、
【知识点】逆命题
12.【答案】一边上的高线与这边对角的角平分线重合的三角形是等腰三角形;如图,AD⊥BC,AD是△ABC的角平分线 ;△ABC是等腰三角形。;∵AD是△ABC的角平分线, ∴∠BAD=∠CAD, 在△ADC和△ADB中, , ∴△ADC≌△ADB(AAS), ∴AB=AC, ∴△ABC是等腰三角形.
【知识点】真命题与假命题;逆命题
13.【答案】(1)解:题设是两条直线都与第三条直线平行,结论是这两条直线也互相平行
(2)解:“相交的两条直线一定不平行”可改写为“如果两条直线相交,那么它们一定不平行”,
故题设是两条直线相交,结论是它们一定不平行.
【知识点】定义、命题、定理、推论的概念
14.【答案】(1)解:如果两个角是对顶角,那么这两个角相等,
条件:两个角是对顶角,结论:这两个角相等
(2)解:如果两个角都是同一个角的余角,那么这两个角相等.
条件:两个角都是同一个角的余角,
结论:这两个角相等
(3)解:如果三个角是一个三角形的内角,那么这三个内角和等于180°.
条件:三个角是一个三角形的内角,
结论:这三个内角和等于180°
(4)解:如果一个点在角平分线上,那么它到角两边的距离相等.
条件:一个点在角平分线上,
结论:这个点到角两边的距离相等
【知识点】定义、命题、定理、推论的概念
15.【答案】(1)正确
(2)正确
(3)错误
(4)正确
(5)正确
(6)正确
(7)错误
(8)正确
【知识点】定义、命题、定理、推论的概念
16.【答案】错误
【知识点】三角形外角的概念及性质
17.【答案】可求出∠A=40°.
【知识点】三角形外角的概念及性质
18.【答案】(1); (2)
【知识点】三角形外角的概念及性质
19.【答案】
【知识点】三角形内角和定理;三角形外角的概念及性质
20.【答案】44°
【知识点】三角形内角和定理;三角形外角的概念及性质
21.【答案】(1)
(2)解:,理由如下:如下图,
∵,
∴,
又∵,
∴,
∴,
故答案为:;
(3)解:由题意得:如果两个角的两边分别平行,那么这两个角相等或者互补.
【知识点】平行线的性质;定义、命题、定理、推论的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
