15.3角的平分线 同步练习(含答案)
文档属性
| 名称 | 15.3角的平分线 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 529.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 15:06:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
15.3 角的平分线
一、单选题
1.如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A.PC>PD B.PC=PD C.PC2.如图,∠B+∠DCB=180°,AC平分∠DAB,且∠D∶∠DAC=5∶2,则∠D的度数是( )
A.100° B.105° C.110° D.120°
3.如图, 是 的角平分线, ,垂足为 , , , ,则 的面积为( )
A.4 B.6 C.8 D.10
4.下面是“作角的平分线”的尺规作图方法:
(1)如图,以点为圆心,任意长为半径画弧,分别交,于点,;
(2)分别以,为圆心,以大于的同样长为半径作弧,两弧交于点;
(3)作射线.
所以射线即为所求.
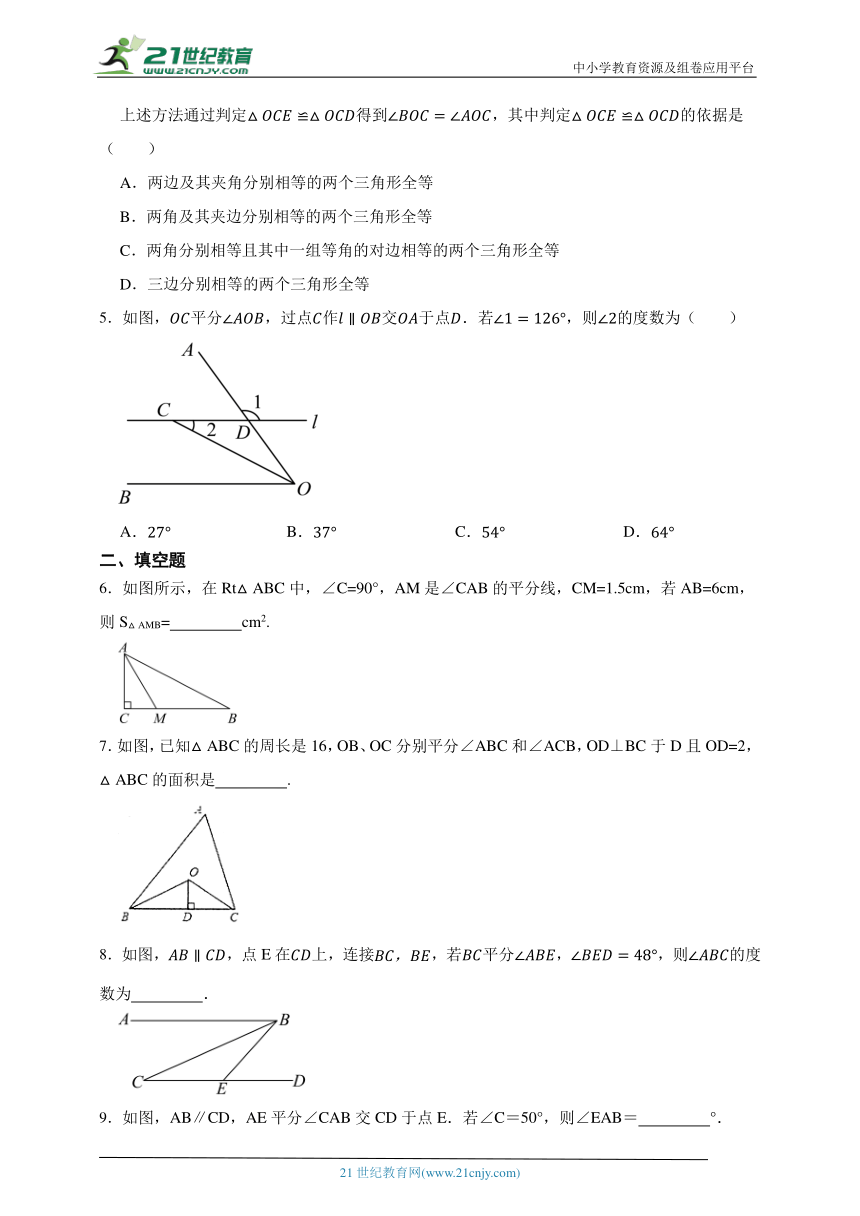
上述方法通过判定得到,其中判定的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两角分别相等且其中一组等角的对边相等的两个三角形全等
D.三边分别相等的两个三角形全等
5.如图,平分,过点作交于点.若,则的度数为( )
A. B. C. D.
二、填空题
6.如图所示,在Rt△ABC中,∠C=90°,AM是∠CAB的平分线,CM=1.5cm,若AB=6cm,则S△AMB= cm2.
7.如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是 .
8.如图,,点E在上,连接,若平分,,则的度数为 .
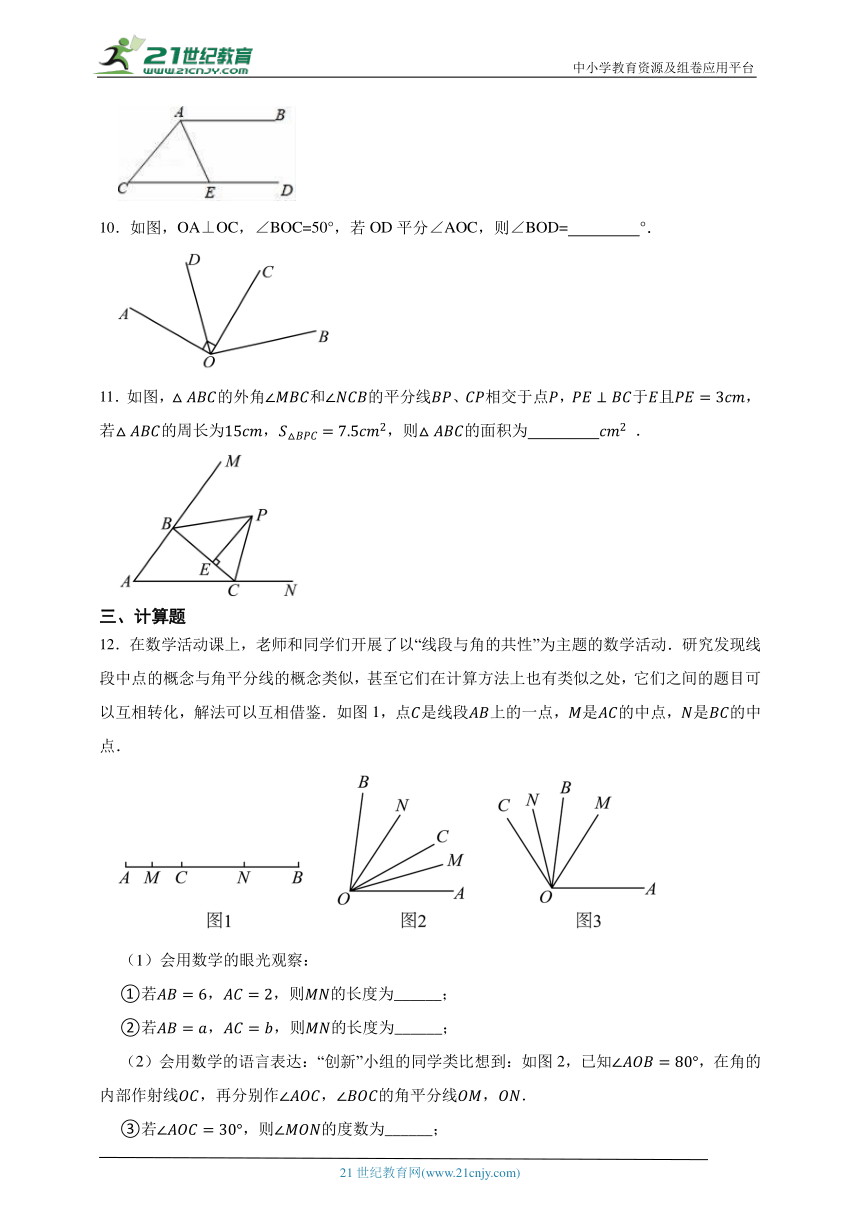
9.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠EAB= °.
10.如图,OA⊥OC,∠BOC=50°,若OD平分∠AOC,则∠BOD= °.
11.如图,的外角和的平分线、相交于点,于且,若的周长为,,则的面积为 .
三、计算题
12.在数学活动课上,老师和同学们开展了以“线段与角的共性”为主题的数学活动.研究发现线段中点的概念与角平分线的概念类似,甚至它们在计算方法上也有类似之处,它们之间的题目可以互相转化,解法可以互相借鉴.如图1,点是线段上的一点,是的中点,是的中点.
(1)会用数学的眼光观察:
①若,,则的长度为______;
②若,,则的长度为______;
(2)会用数学的语言表达:“创新”小组的同学类比想到:如图2,已知,在角的内部作射线,再分别作,的角平分线,.
③若,则的度数为______;
④若,则的度数为______;
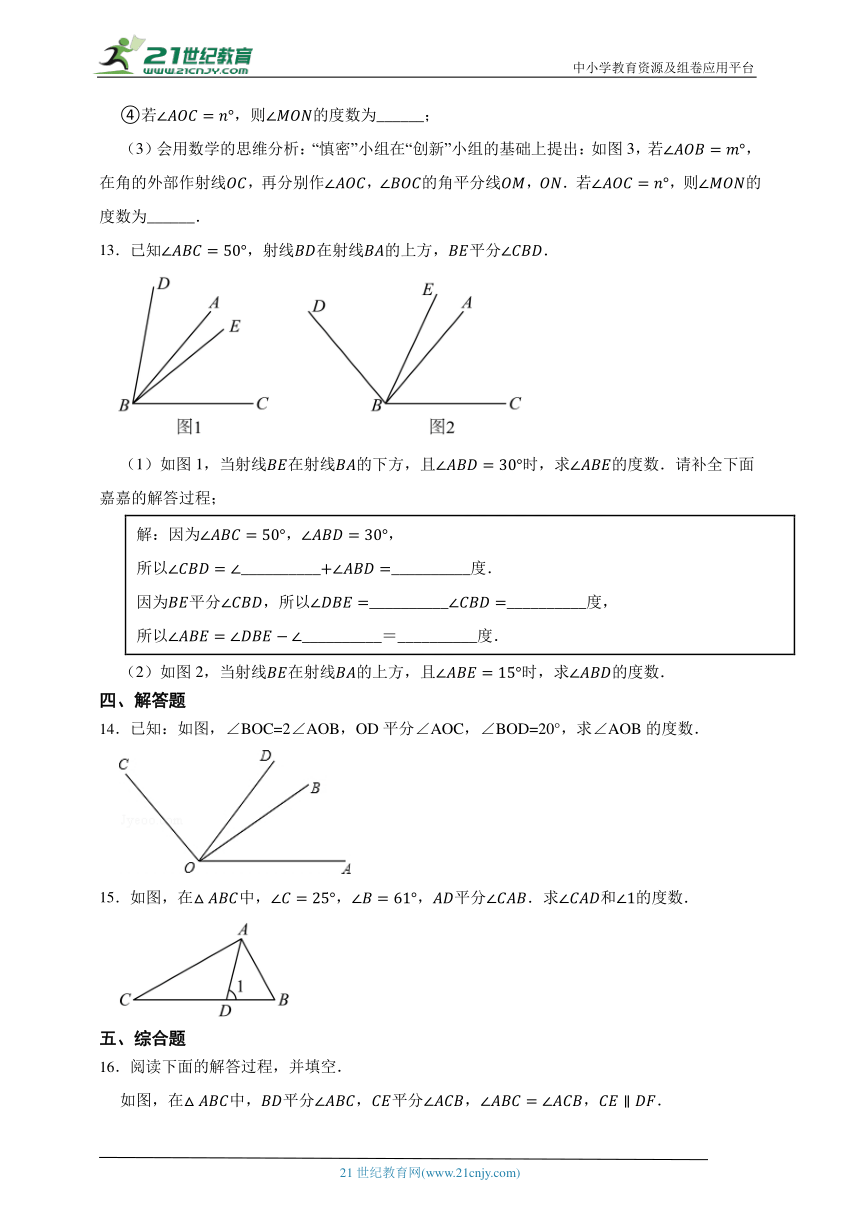
(3)会用数学的思维分析:“慎密”小组在“创新”小组的基础上提出:如图3,若,在角的外部作射线,再分别作,的角平分线,.若,则的度数为______.
13.已知,射线在射线的上方,平分.
(1)如图1,当射线在射线的下方,且时,求的度数.请补全下面嘉嘉的解答过程;
解:因为,, 所以____________________度. 因为平分,所以____________________度, 所以__________=__________度.
(2)如图2,当射线在射线的上方,且时,求的度数.
四、解答题
14.已知:如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,求∠AOB的度数.
15.如图,在中,,,平分.求和的度数.
五、综合题
16.阅读下面的解答过程,并填空.
如图,在中,平分,平分,,.
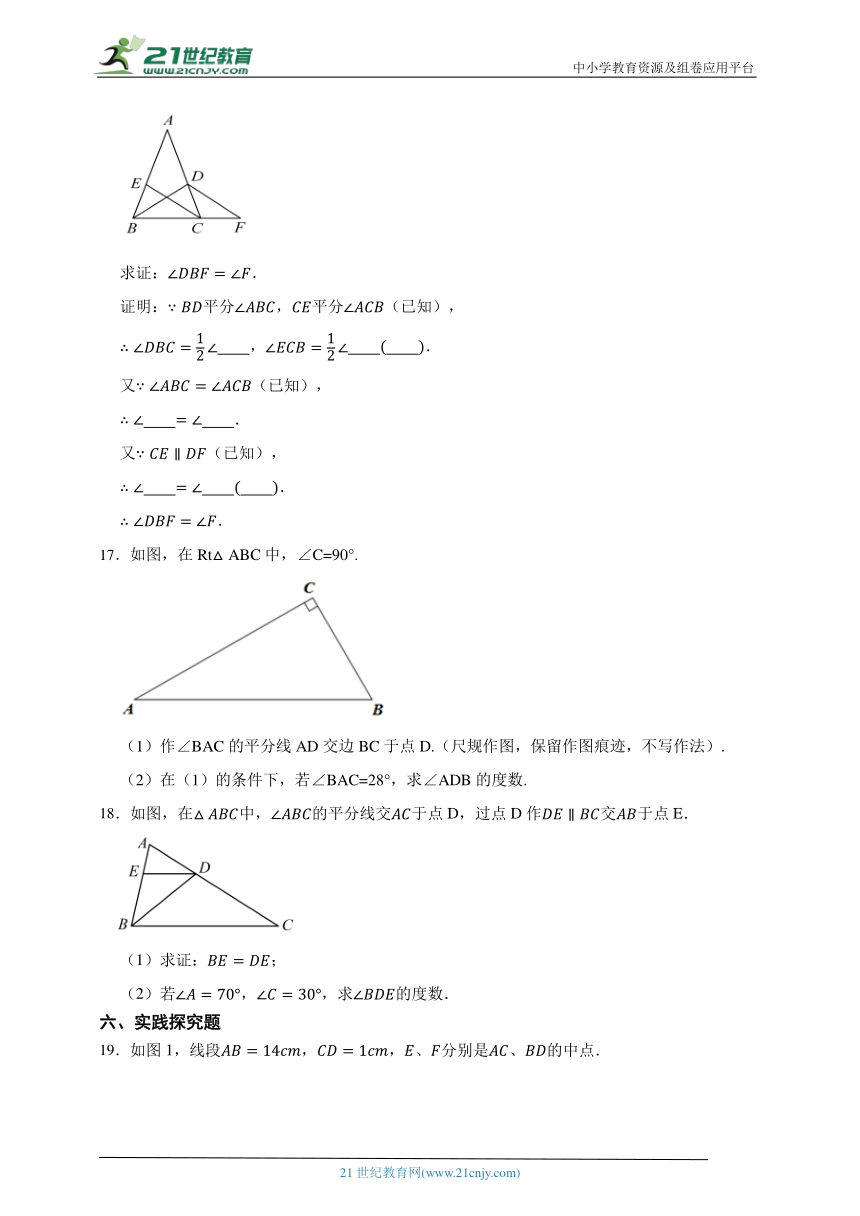
求证:.
证明:平分,平分(已知),
, .
又(已知),
.
又(已知),
.
.
17.如图,在Rt△ABC中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).
(2)在(1)的条件下,若∠BAC=28°,求∠ADB的度数.
18.如图,在中,的平分线交于点D,过点D作交于点E.
(1)求证:;
(2)若,,求的度数.
六、实践探究题
19.如图1,线段,,、分别是、的中点.
【问题发现】
(1)若,则________.
【拓展探究】
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变,求出的长度;如果变化,请说明理由.
【问题解决】
(3)我们发现角的很多规律和线段一样,如图2,、分别平分和.若,,求的度数.
答案解析部分
1.【答案】B
【知识点】角平分线的性质
2.【答案】A
【知识点】平行线的判定与性质;角平分线的性质
3.【答案】D
【知识点】三角形的面积;角平分线的性质
4.【答案】D
【知识点】三角形全等的判定-SSS;尺规作图-作角的平分线
5.【答案】A
【知识点】平行线的性质;角平分线的性质;邻补角
6.【答案】4.5
【知识点】角平分线的应用
7.【答案】16
【知识点】角平分线的性质;角平分线的应用
8.【答案】
【知识点】角平分线的性质;内错角的概念
9.【答案】65
【知识点】平行线的性质;角平分线的性质
10.【答案】95
【知识点】角平分线的性质
11.【答案】7.5
【知识点】角平分线的性质
12.【答案】(1)①3;②
(2)③;④
(3)
【知识点】角平分线的性质;线段的中点
13.【答案】(1);80;;40;;10
(2).
【知识点】角的运算;角平分线的性质
14.【答案】40°
【知识点】角平分线的性质;一元一次方程的实际应用-几何问题
15.【答案】,
【知识点】三角形内角和定理;三角形外角的概念及性质;角平分线的性质
16.【答案】,,角平分线定义,,,,,两直线平行,同位角相等.
【知识点】平行线的判定与性质;三角形内角和定理;角平分线的性质
17.【答案】(1)解:以A为圆心,以任意长为半径画弧,分别交AC,AB于M、N,再分别以M、N为圆心,以大于MN长的一半为半径画弧,两者交于点P,连接AP并延长与BC交于D,即为所求;
(2)∵∠C=90°,∠BAC=28°,
∴∠B=180°-∠C-∠BAC=62°,
∵AD平分∠BAC,
∴ ,
∴∠ADB=180°-∠BAD-∠B=104°.
【知识点】三角形内角和定理;角平分线的概念;尺规作图-作角的平分线
18.【答案】(1)证明:∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ;
(2)解:∵ , ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴
【知识点】平行线的判定;三角形内角和定理;角平分线的性质
19.【答案】(1) (2)的长度不变 (3)
【知识点】角的运算;角平分线的性质;线段的中点;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
15.3 角的平分线
一、单选题
1.如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A.PC>PD B.PC=PD C.PC
A.100° B.105° C.110° D.120°
3.如图, 是 的角平分线, ,垂足为 , , , ,则 的面积为( )
A.4 B.6 C.8 D.10
4.下面是“作角的平分线”的尺规作图方法:
(1)如图,以点为圆心,任意长为半径画弧,分别交,于点,;
(2)分别以,为圆心,以大于的同样长为半径作弧,两弧交于点;
(3)作射线.
所以射线即为所求.
上述方法通过判定得到,其中判定的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两角分别相等且其中一组等角的对边相等的两个三角形全等
D.三边分别相等的两个三角形全等
5.如图,平分,过点作交于点.若,则的度数为( )
A. B. C. D.
二、填空题
6.如图所示,在Rt△ABC中,∠C=90°,AM是∠CAB的平分线,CM=1.5cm,若AB=6cm,则S△AMB= cm2.
7.如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是 .
8.如图,,点E在上,连接,若平分,,则的度数为 .
9.如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C=50°,则∠EAB= °.
10.如图,OA⊥OC,∠BOC=50°,若OD平分∠AOC,则∠BOD= °.
11.如图,的外角和的平分线、相交于点,于且,若的周长为,,则的面积为 .
三、计算题
12.在数学活动课上,老师和同学们开展了以“线段与角的共性”为主题的数学活动.研究发现线段中点的概念与角平分线的概念类似,甚至它们在计算方法上也有类似之处,它们之间的题目可以互相转化,解法可以互相借鉴.如图1,点是线段上的一点,是的中点,是的中点.
(1)会用数学的眼光观察:
①若,,则的长度为______;
②若,,则的长度为______;
(2)会用数学的语言表达:“创新”小组的同学类比想到:如图2,已知,在角的内部作射线,再分别作,的角平分线,.
③若,则的度数为______;
④若,则的度数为______;
(3)会用数学的思维分析:“慎密”小组在“创新”小组的基础上提出:如图3,若,在角的外部作射线,再分别作,的角平分线,.若,则的度数为______.
13.已知,射线在射线的上方,平分.
(1)如图1,当射线在射线的下方,且时,求的度数.请补全下面嘉嘉的解答过程;
解:因为,, 所以____________________度. 因为平分,所以____________________度, 所以__________=__________度.
(2)如图2,当射线在射线的上方,且时,求的度数.
四、解答题
14.已知:如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,求∠AOB的度数.
15.如图,在中,,,平分.求和的度数.
五、综合题
16.阅读下面的解答过程,并填空.
如图,在中,平分,平分,,.
求证:.
证明:平分,平分(已知),
, .
又(已知),
.
又(已知),
.
.
17.如图,在Rt△ABC中,∠C=90°.
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).
(2)在(1)的条件下,若∠BAC=28°,求∠ADB的度数.
18.如图,在中,的平分线交于点D,过点D作交于点E.
(1)求证:;
(2)若,,求的度数.
六、实践探究题
19.如图1,线段,,、分别是、的中点.
【问题发现】
(1)若,则________.
【拓展探究】
(2)当线段在线段上运动时,试判断的长度是否发生变化?如果不变,求出的长度;如果变化,请说明理由.
【问题解决】
(3)我们发现角的很多规律和线段一样,如图2,、分别平分和.若,,求的度数.
答案解析部分
1.【答案】B
【知识点】角平分线的性质
2.【答案】A
【知识点】平行线的判定与性质;角平分线的性质
3.【答案】D
【知识点】三角形的面积;角平分线的性质
4.【答案】D
【知识点】三角形全等的判定-SSS;尺规作图-作角的平分线
5.【答案】A
【知识点】平行线的性质;角平分线的性质;邻补角
6.【答案】4.5
【知识点】角平分线的应用
7.【答案】16
【知识点】角平分线的性质;角平分线的应用
8.【答案】
【知识点】角平分线的性质;内错角的概念
9.【答案】65
【知识点】平行线的性质;角平分线的性质
10.【答案】95
【知识点】角平分线的性质
11.【答案】7.5
【知识点】角平分线的性质
12.【答案】(1)①3;②
(2)③;④
(3)
【知识点】角平分线的性质;线段的中点
13.【答案】(1);80;;40;;10
(2).
【知识点】角的运算;角平分线的性质
14.【答案】40°
【知识点】角平分线的性质;一元一次方程的实际应用-几何问题
15.【答案】,
【知识点】三角形内角和定理;三角形外角的概念及性质;角平分线的性质
16.【答案】,,角平分线定义,,,,,两直线平行,同位角相等.
【知识点】平行线的判定与性质;三角形内角和定理;角平分线的性质
17.【答案】(1)解:以A为圆心,以任意长为半径画弧,分别交AC,AB于M、N,再分别以M、N为圆心,以大于MN长的一半为半径画弧,两者交于点P,连接AP并延长与BC交于D,即为所求;
(2)∵∠C=90°,∠BAC=28°,
∴∠B=180°-∠C-∠BAC=62°,
∵AD平分∠BAC,
∴ ,
∴∠ADB=180°-∠BAD-∠B=104°.
【知识点】三角形内角和定理;角平分线的概念;尺规作图-作角的平分线
18.【答案】(1)证明:∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ;
(2)解:∵ , ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴
【知识点】平行线的判定;三角形内角和定理;角平分线的性质
19.【答案】(1) (2)的长度不变 (3)
【知识点】角的运算;角平分线的性质;线段的中点;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
