2025年秋期沪科版数学(2024)八年级上册期末试题(含答案)
文档属性
| 名称 | 2025年秋期沪科版数学(2024)八年级上册期末试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 628.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年秋期沪科版数学(2024)八年级上册期末试题
一、单选题
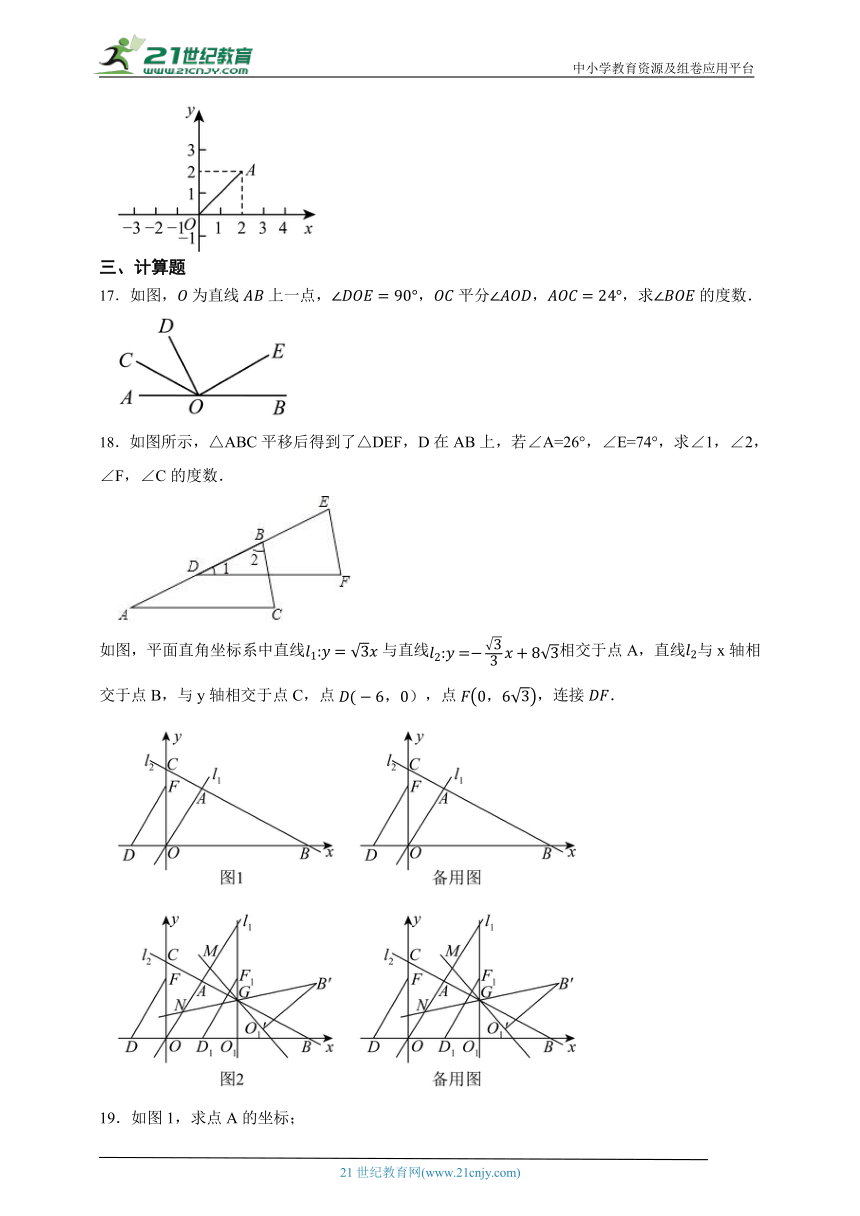
1.以下图形是轴对称图形的是( )
A. B. C. D.
2.若点在第一象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,在中,,分别以点,点为圆心,大于长为半径画弧,两弧交于,两点,作直线交于点,连接.若平分,则的度数为( )
A. B. C. D.
4.对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标志等作品的设计上,使对称之美惊艳了千年的时光.下列常见的运动图标是轴对称图形的是( )
A. B.
C. D.
5.如图,△OAC≌△OBD.若OC=12,OB=7,则AD=( )
A.5 B.6 C.7 D.8
6.若,,,则的大小为( )
A. B. C. D.
7.点在二、四象限的角平分线上,则( )
A. B.2 C. D.
8.如图所示,在中,,高,高交于点.若,,则的长度为( )
A.1.2 B.1.3 C.1.4 D.1.8
9.张院士的动力科学研究院实验基地内装有一段笔直的轨道,长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为,滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿,然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为,右端离点的距离为,记,与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数:滑块从点出发到最后返回点,整个过程总用时(含停顿时间).若在整个往返过程中,,则( ).
A.6或9 B.18 C.6或18 D.9或18
10.如图,为线段上一动点(不与点重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连接.下列结论①;②;③是等边三角形;④;⑤平分.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.在镜子中看到时钟显示的时间是,则实际时间是
12.已知点在x轴上,则a的值为 .
13.一次函数的图象与轴的交点坐标是 .
14.如图,在平面直角坐标系中,为原点,点,点,且.将线段平移后,平移后,的对应点分别为点,,其中.连接,,若点在直线上运动.连接,记三角形的面积为,其中,则的取值范围是 .
15. 如图,已知∠MON=30°,点A1,A2,A3 …在射线ON上,点B1、B2、B3 …在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=2,则△A4B4A5的边长是 .
16.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有 个.
三、计算题
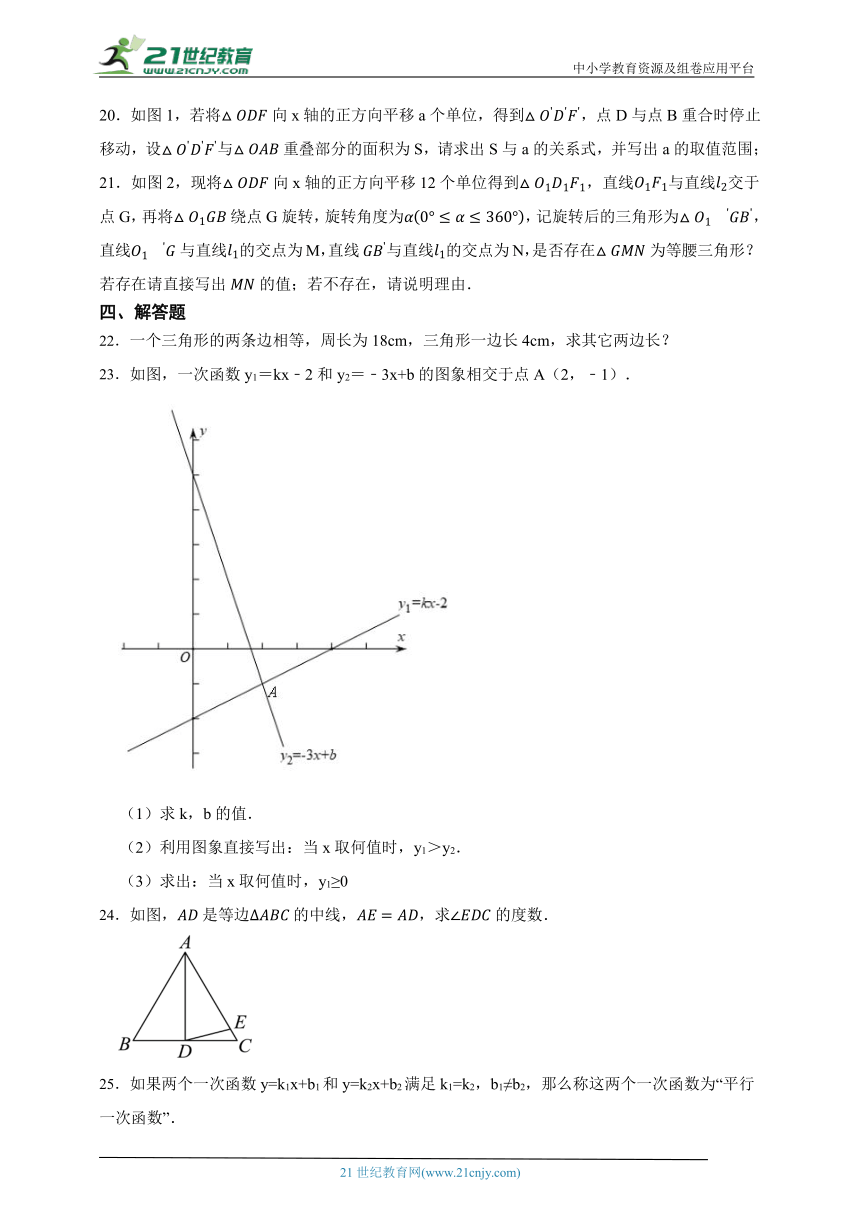
17.如图,为直线上一点,,平分,,求的度数.
18.如图所示,△ABC平移后得到了△DEF,D在AB上,若∠A=26°,∠E=74°,求∠1,∠2,∠F,∠C的度数.
如图,平面直角坐标系中直线与直线相交于点A,直线与x轴相交于点B,与y轴相交于点C,点,点,连接.
19.如图1,求点A的坐标;
20.如图1,若将向x轴的正方向平移a个单位,得到,点D与点B重合时停止移动,设与重叠部分的面积为S,请求出S与a的关系式,并写出a的取值范围;
21.如图2,现将向x轴的正方向平移12个单位得到,直线与直线交于点G,再将绕点G旋转,旋转角度为,记旋转后的三角形为,直线与直线的交点为M,直线与直线的交点为N,是否存在为等腰三角形?若存在请直接写出的值;若不存在,请说明理由.
四、解答题
22.一个三角形的两条边相等,周长为18cm,三角形一边长4cm,求其它两边长?
23.如图,一次函数y1=kx﹣2和y2=﹣3x+b的图象相交于点A(2,﹣1).
(1)求k,b的值.
(2)利用图象直接写出:当x取何值时,y1>y2.
(3)求出:当x取何值时,y1≥0
24.如图,是等边的中线,,求的度数.
25.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的,求y=kx+b的解析式.
26.我校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,若购买1张两人学习桌,1张三人学习桌需380元;若购买3张两人学习桌,2张三人学习桌需940元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过4700元,购买两种学习桌共25张,以至少满足58名学生的需求,有几种购买方案?并求哪种购买方案费用最低?
27.直线EF、GH之间有一个直角三角形ABC,其中∠BAC=90°,∠ABC=α。
(1)如图1,点A在直线EF上,B、C在直线GH上,若∠α=60°,∠FAC=30°。试说明:EF∥GH;
(2)将三角形ABC如图2放置,直线EF∥GH,点C、B分别在直线EF、GH上,且BC平分∠ABH。求∠ECA的度数;(用α的代数式表示)
(3)在(2)的前提下,直线CD平分∠FCA交直线GH于D,如图3,在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化请求出变化的范围。
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】B
【知识点】点的坐标与象限的关系
3.【答案】D
【知识点】三角形内角和定理;角平分线的性质;线段垂直平分线的性质
4.【答案】A
【知识点】轴对称图形
5.【答案】A
【知识点】三角形全等及其性质
6.【答案】A
【知识点】三角形内角和定理;三角形全等及其性质
7.【答案】A
【知识点】点的坐标与象限的关系
8.【答案】C
【知识点】三角形全等及其性质
9.【答案】C
【知识点】一次函数的实际应用-行程问题
10.【答案】D
【知识点】平行线的判定;等边三角形的判定与性质;角平分线的判定;三角形全等的判定-SAS
11.【答案】16:25:08
【知识点】作图﹣轴对称
12.【答案】
【知识点】点的坐标与象限的关系
13.【答案】(0,-3).
【知识点】一次函数图象与坐标轴交点问题
14.【答案】或
【知识点】坐标与图形性质;平移的性质;坐标与图形变化﹣平移
15.【答案】16
【知识点】三角形外角的概念及性质;等腰三角形的判定;等边三角形的性质
16.【答案】4
【知识点】等腰三角形的判定
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】解:∵△ABC平移后得到△DEF,∠A=26°,∠E=74°,
∴∠A=∠1=26°,∠E=∠2=74°
∴∠C=∠F=180°﹣26°﹣74°=80°
【知识点】三角形内角和定理;平移的性质
【答案】19.
20.
21.存在,或
【知识点】等边三角形的性质;含30°角的直角三角形;一次函数的实际应用-几何问题
22.【答案】解:①当4为腰时,三边为4,4,10,4+4<10,不满足三角形三边关系;②当4为底时,三边为4,7,7,满足三角形三边关系,则其它两边长为7cm,7cm.
【知识点】三角形三边关系;等腰三角形的性质
23.【答案】(1),;
(2);
(3).
【知识点】解一元一次不等式;待定系数法求一次函数解析式;一次函数与不等式(组)的关系
24.【答案】.
【知识点】等边三角形的性质;等腰三角形的性质-三线合一
25.【答案】(1)7;(2)y=﹣2x+2或y=﹣2x﹣2
【知识点】一次函数的实际应用-几何问题
26.【答案】(1)每张两人学习桌180元,每张三人学习桌200元;(2)有3种购买方案,当购买17张两人桌,8张三人桌的费用最低,最低费用为4660元.
【知识点】一元一次不等式的应用;一次函数的实际应用-方案问题;二元一次方程组的实际应用-方案选择题问题
27.【答案】(1)证明:∵∠EAB=180°-∠BAC-∠FAC,∠BAC=90°,∠FAC=30°,
∴∠EAB=60°,
又∵∠ABC=60°,
∴∠EAB=∠ABC,
∴EF∥GH;
(2)解:经过点A作AM∥GH,
又∵EF∥GH,
∴AM∥EF∥GH,
∵BC平分∠ABH
∴∠ABC=∠CBH=a
∴∠MAB=180°-∠ABH=180°-2a
∴∠MAC=90°-(180°-2a)=2a-90°
∴∠ECA=∠MAC=2a-90°
(3)解:不发生变化,
由(2)得:∠ECA=2a-90°,
∴∠FCA=180°-(2a-90°)=270°-2a
∵CD平分∠FCA,
∴∠FCD=135°-a,
∵EF//GH
∴∠FCB+∠CBH=180°,
∴∠FCB=180°-a,
∴∠BCD=180°-a-(135°-a)=45
【知识点】平行线的性质;角平分线的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年秋期沪科版数学(2024)八年级上册期末试题
一、单选题
1.以下图形是轴对称图形的是( )
A. B. C. D.
2.若点在第一象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,在中,,分别以点,点为圆心,大于长为半径画弧,两弧交于,两点,作直线交于点,连接.若平分,则的度数为( )
A. B. C. D.
4.对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标志等作品的设计上,使对称之美惊艳了千年的时光.下列常见的运动图标是轴对称图形的是( )
A. B.
C. D.
5.如图,△OAC≌△OBD.若OC=12,OB=7,则AD=( )
A.5 B.6 C.7 D.8
6.若,,,则的大小为( )
A. B. C. D.
7.点在二、四象限的角平分线上,则( )
A. B.2 C. D.
8.如图所示,在中,,高,高交于点.若,,则的长度为( )
A.1.2 B.1.3 C.1.4 D.1.8
9.张院士的动力科学研究院实验基地内装有一段笔直的轨道,长度为的金属滑块在上面做往返滑动.如图,滑块首先沿方向从左向右匀速滑动,滑动速度为,滑动开始前滑块左端与点重合,当滑块右端到达点时,滑块停顿,然后再以小于的速度匀速返回,直到滑块的左端与点重合,滑动停止.设时间为时,滑块左端离点的距离为,右端离点的距离为,记,与具有函数关系.已知滑块在从左向右滑动过程中,当和时,与之对应的的两个值互为相反数:滑块从点出发到最后返回点,整个过程总用时(含停顿时间).若在整个往返过程中,,则( ).
A.6或9 B.18 C.6或18 D.9或18
10.如图,为线段上一动点(不与点重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连接.下列结论①;②;③是等边三角形;④;⑤平分.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.在镜子中看到时钟显示的时间是,则实际时间是
12.已知点在x轴上,则a的值为 .
13.一次函数的图象与轴的交点坐标是 .
14.如图,在平面直角坐标系中,为原点,点,点,且.将线段平移后,平移后,的对应点分别为点,,其中.连接,,若点在直线上运动.连接,记三角形的面积为,其中,则的取值范围是 .
15. 如图,已知∠MON=30°,点A1,A2,A3 …在射线ON上,点B1、B2、B3 …在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=2,则△A4B4A5的边长是 .
16.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P有 个.
三、计算题
17.如图,为直线上一点,,平分,,求的度数.
18.如图所示,△ABC平移后得到了△DEF,D在AB上,若∠A=26°,∠E=74°,求∠1,∠2,∠F,∠C的度数.
如图,平面直角坐标系中直线与直线相交于点A,直线与x轴相交于点B,与y轴相交于点C,点,点,连接.
19.如图1,求点A的坐标;
20.如图1,若将向x轴的正方向平移a个单位,得到,点D与点B重合时停止移动,设与重叠部分的面积为S,请求出S与a的关系式,并写出a的取值范围;
21.如图2,现将向x轴的正方向平移12个单位得到,直线与直线交于点G,再将绕点G旋转,旋转角度为,记旋转后的三角形为,直线与直线的交点为M,直线与直线的交点为N,是否存在为等腰三角形?若存在请直接写出的值;若不存在,请说明理由.
四、解答题
22.一个三角形的两条边相等,周长为18cm,三角形一边长4cm,求其它两边长?
23.如图,一次函数y1=kx﹣2和y2=﹣3x+b的图象相交于点A(2,﹣1).
(1)求k,b的值.
(2)利用图象直接写出:当x取何值时,y1>y2.
(3)求出:当x取何值时,y1≥0
24.如图,是等边的中线,,求的度数.
25.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的,求y=kx+b的解析式.
26.我校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,若购买1张两人学习桌,1张三人学习桌需380元;若购买3张两人学习桌,2张三人学习桌需940元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过4700元,购买两种学习桌共25张,以至少满足58名学生的需求,有几种购买方案?并求哪种购买方案费用最低?
27.直线EF、GH之间有一个直角三角形ABC,其中∠BAC=90°,∠ABC=α。
(1)如图1,点A在直线EF上,B、C在直线GH上,若∠α=60°,∠FAC=30°。试说明:EF∥GH;
(2)将三角形ABC如图2放置,直线EF∥GH,点C、B分别在直线EF、GH上,且BC平分∠ABH。求∠ECA的度数;(用α的代数式表示)
(3)在(2)的前提下,直线CD平分∠FCA交直线GH于D,如图3,在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化请求出变化的范围。
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】B
【知识点】点的坐标与象限的关系
3.【答案】D
【知识点】三角形内角和定理;角平分线的性质;线段垂直平分线的性质
4.【答案】A
【知识点】轴对称图形
5.【答案】A
【知识点】三角形全等及其性质
6.【答案】A
【知识点】三角形内角和定理;三角形全等及其性质
7.【答案】A
【知识点】点的坐标与象限的关系
8.【答案】C
【知识点】三角形全等及其性质
9.【答案】C
【知识点】一次函数的实际应用-行程问题
10.【答案】D
【知识点】平行线的判定;等边三角形的判定与性质;角平分线的判定;三角形全等的判定-SAS
11.【答案】16:25:08
【知识点】作图﹣轴对称
12.【答案】
【知识点】点的坐标与象限的关系
13.【答案】(0,-3).
【知识点】一次函数图象与坐标轴交点问题
14.【答案】或
【知识点】坐标与图形性质;平移的性质;坐标与图形变化﹣平移
15.【答案】16
【知识点】三角形外角的概念及性质;等腰三角形的判定;等边三角形的性质
16.【答案】4
【知识点】等腰三角形的判定
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】解:∵△ABC平移后得到△DEF,∠A=26°,∠E=74°,
∴∠A=∠1=26°,∠E=∠2=74°
∴∠C=∠F=180°﹣26°﹣74°=80°
【知识点】三角形内角和定理;平移的性质
【答案】19.
20.
21.存在,或
【知识点】等边三角形的性质;含30°角的直角三角形;一次函数的实际应用-几何问题
22.【答案】解:①当4为腰时,三边为4,4,10,4+4<10,不满足三角形三边关系;②当4为底时,三边为4,7,7,满足三角形三边关系,则其它两边长为7cm,7cm.
【知识点】三角形三边关系;等腰三角形的性质
23.【答案】(1),;
(2);
(3).
【知识点】解一元一次不等式;待定系数法求一次函数解析式;一次函数与不等式(组)的关系
24.【答案】.
【知识点】等边三角形的性质;等腰三角形的性质-三线合一
25.【答案】(1)7;(2)y=﹣2x+2或y=﹣2x﹣2
【知识点】一次函数的实际应用-几何问题
26.【答案】(1)每张两人学习桌180元,每张三人学习桌200元;(2)有3种购买方案,当购买17张两人桌,8张三人桌的费用最低,最低费用为4660元.
【知识点】一元一次不等式的应用;一次函数的实际应用-方案问题;二元一次方程组的实际应用-方案选择题问题
27.【答案】(1)证明:∵∠EAB=180°-∠BAC-∠FAC,∠BAC=90°,∠FAC=30°,
∴∠EAB=60°,
又∵∠ABC=60°,
∴∠EAB=∠ABC,
∴EF∥GH;
(2)解:经过点A作AM∥GH,
又∵EF∥GH,
∴AM∥EF∥GH,
∵BC平分∠ABH
∴∠ABC=∠CBH=a
∴∠MAB=180°-∠ABH=180°-2a
∴∠MAC=90°-(180°-2a)=2a-90°
∴∠ECA=∠MAC=2a-90°
(3)解:不发生变化,
由(2)得:∠ECA=2a-90°,
∴∠FCA=180°-(2a-90°)=270°-2a
∵CD平分∠FCA,
∴∠FCD=135°-a,
∵EF//GH
∴∠FCB+∠CBH=180°,
∴∠FCB=180°-a,
∴∠BCD=180°-a-(135°-a)=45
【知识点】平行线的性质;角平分线的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
