12.1函数 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
12.1 函数
一、单选题
1.汽车以每小时100千米的速度匀速行驶,行驶的路程随时间的变化而变化,在这个变化过程中,自变量是( )
A.汽车 B.路程 C.速度 D.时间
2.某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
3.函数的自变量x的取值范围是( )
A. B.且
C. D.x可取任意实数
4.在函数中,自变量的取值范围是( )
A. B. C. D.
5.函数的自变量的取值范围是( )
A. B. C. D.
二、填空题
6.小亮从家匀速跑步到学校,接着马上原路匀速步行回家,已知小亮步行回家的时间是跑步到学校时间的2倍.如图是小亮离家的路程与时间的函数图象,则小亮回家的速度是每分钟步行 m.
7.已知,那么.
8.函数的定义域是 .
9.“二十四节气”是华夏祖先历经千百年的实践创造出来的宝贵遗产,它与白昼时长密切相关,是反映天气气候和物候变化、掌握农事季节的工具.如图所示是一年中部分节气所对应的白昼时长示意图,则立春、清明、寒露、小寒这四个节气中,白昼时长最短的节气是 .
10.购买一些双面胶,单价为2元/卷,请写出总价元随双面胶卷数变化的解析式: .
11.在函数 中,自变量x的取值范固是 .
三、计算题
12.2018年5月14日川航3U8633航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度(千米)与相应高度处气温(℃)的关系【成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米】.
海拔高度(千米) 0 1 2 3 4 5 …
气温(℃) 20 14 8 2 …
根据上表,回答以下问题:
(1)由上表可知海拔4千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温与海坺高度的关系式为____________.
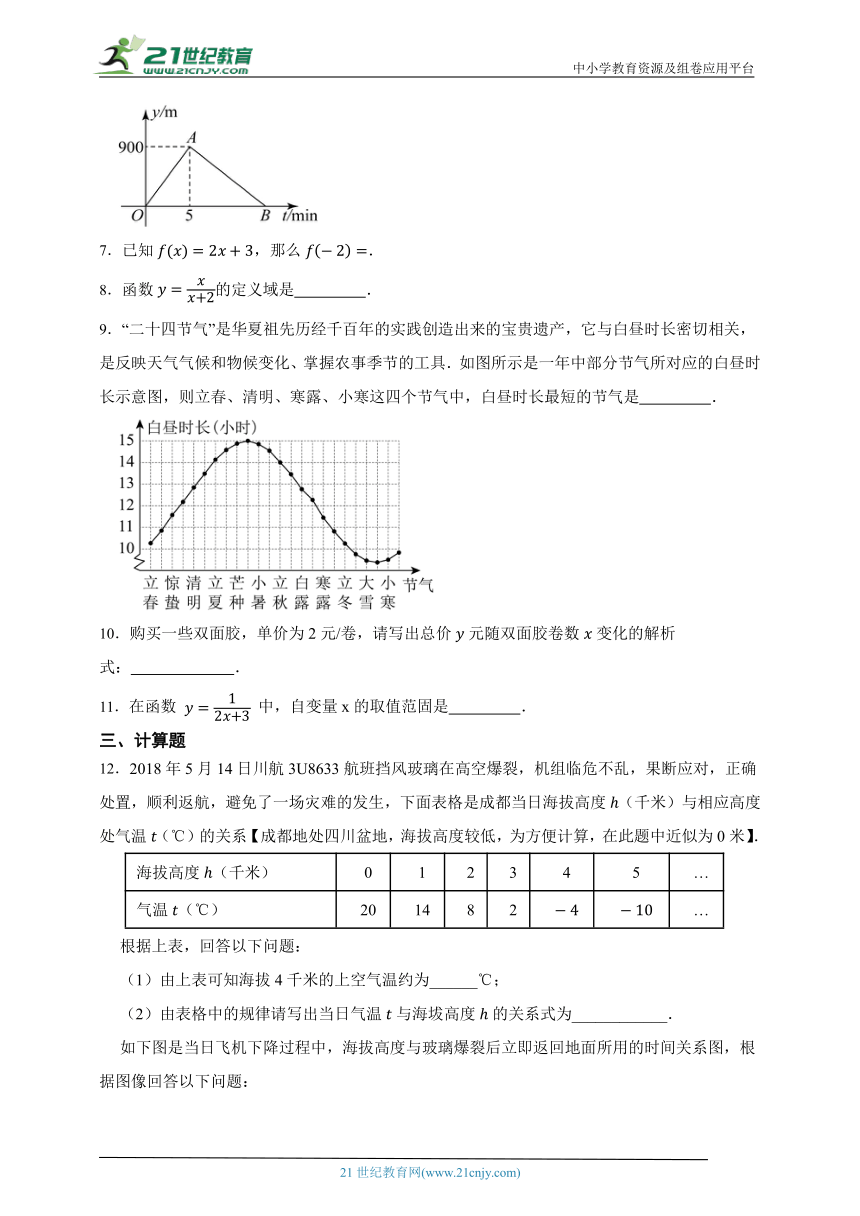
如下图是当日飞机下降过程中,海拔高度与玻璃爆裂后立即返回地面所用的时间关系图,根据图像回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米?
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了非常大的艰险.
13.已知函数,计算和时,哪一个对应的函数值较大?
四、解答题
14.一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2 m/s,到达坡底时小球的速度达到40 m/s.
(1)求小球的速度v(m/s)与时间t(s)之间的函数关系式;
(2)求t的取值范围;
(3)求3.5 s时小球的速度;
(4)求t(s)时小球的速度为16 m/s.
15.如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
数量/只 1 2 3 4 5 …
高度/cm 4 5.2 6.4 7.6 8.8 …
(1)上述两个变量之间的关系中,哪个是自变量?哪个是因变量?
(2)用 h(cm)表示这摞碗的高度,用 x(只)表示这摞碗的数量,请用含有 x 的代数式表示 h;
(3)若这摞碗的高度为 11.2cm,求这摞碗的数量.
五、综合题
16.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
17.某市出租车采取分段收费方式:起步价为a元,即路程不超过b千米时收费a元,超过部分每千米收费c元乘车费与行驶路程之间的关系如图所示,请根据图象回答下列问题:
(1)由图象知, , , ;
(2)小明乘坐出租车行驶了23千米,那么他应付 元;
(3)若乘客乘坐出租车的路程为千米时,乘车费为y元,请求出y与x之间的关系式;
(4)若小明共付车费元,那么出租车共行驶 千米.
18.某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
六、实践探究题
19.如图,在中,点D是边的中点,点E是边上的一个动点,连接.设的面积为y,的长为x,小明对变量x和y之间的关系进行了探究,得到了如下的数据:
请根据以上信息,解答下列问题:
x 0 3 6
y 3 0 3
(1)题中的自变量和因变量分别是什么?当时,y的值是多少?直接写出的值;
(2)当的面积为面积的时,求出x的值.
答案解析部分
1.【答案】D
【知识点】常量、变量
2.【答案】D
【知识点】通过函数图象获取信息
3.【答案】B
【知识点】函数自变量的取值范围
4.【答案】A
【知识点】分式有无意义的条件;函数自变量的取值范围
5.【答案】A
【知识点】分式有无意义的条件;函数自变量的取值范围
6.【答案】90
【知识点】通过函数图象获取信息
7.【答案】
【知识点】函数自变量的取值范围
8.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
9.【答案】小寒
【知识点】通过函数图象获取信息
10.【答案】
【知识点】函数解析式
11.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
12.【答案】(1)(2)(3)9.8(4)2(5)
【知识点】通过函数图象获取信息
13.【答案】当x=-2时对应的函数值较大
【知识点】函数自变量的取值范围
14.【答案】(1)v=2t (2)0≤t≤20 (3)7cm/s (4)8s
【知识点】函数解析式;函数自变量的取值范围
15.【答案】(1)碗的数量是自变量,高度是因变量;
(2)h=1.2x+2.8;
(3)7只;
【知识点】函数的概念;函数解析式;函数自变量的取值范围
16.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
17.【答案】(1)8;3;
(2)38
(3)
(4)14
【知识点】函数自变量的取值范围;通过函数图象获取信息;用关系式表示变量间的关系
18.【答案】(1)解:第一天中,从4时到16时这头骆驼的体温是上升的,它的体温从最低上升到最高需要12小时.
(2)解:第三天12时这头骆驼的体温是39 ℃.
【知识点】通过函数图象获取信息
19.【答案】(1)自变量是的长,因变量是的面积;;
(2)或
【知识点】函数的概念;函数自变量的取值范围
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.1 函数
一、单选题
1.汽车以每小时100千米的速度匀速行驶,行驶的路程随时间的变化而变化,在这个变化过程中,自变量是( )
A.汽车 B.路程 C.速度 D.时间
2.某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
3.函数的自变量x的取值范围是( )
A. B.且
C. D.x可取任意实数
4.在函数中,自变量的取值范围是( )
A. B. C. D.
5.函数的自变量的取值范围是( )
A. B. C. D.
二、填空题
6.小亮从家匀速跑步到学校,接着马上原路匀速步行回家,已知小亮步行回家的时间是跑步到学校时间的2倍.如图是小亮离家的路程与时间的函数图象,则小亮回家的速度是每分钟步行 m.
7.已知,那么.
8.函数的定义域是 .
9.“二十四节气”是华夏祖先历经千百年的实践创造出来的宝贵遗产,它与白昼时长密切相关,是反映天气气候和物候变化、掌握农事季节的工具.如图所示是一年中部分节气所对应的白昼时长示意图,则立春、清明、寒露、小寒这四个节气中,白昼时长最短的节气是 .
10.购买一些双面胶,单价为2元/卷,请写出总价元随双面胶卷数变化的解析式: .
11.在函数 中,自变量x的取值范固是 .
三、计算题
12.2018年5月14日川航3U8633航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度(千米)与相应高度处气温(℃)的关系【成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米】.
海拔高度(千米) 0 1 2 3 4 5 …
气温(℃) 20 14 8 2 …
根据上表,回答以下问题:
(1)由上表可知海拔4千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温与海坺高度的关系式为____________.
如下图是当日飞机下降过程中,海拔高度与玻璃爆裂后立即返回地面所用的时间关系图,根据图像回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米?
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了非常大的艰险.
13.已知函数,计算和时,哪一个对应的函数值较大?
四、解答题
14.一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2 m/s,到达坡底时小球的速度达到40 m/s.
(1)求小球的速度v(m/s)与时间t(s)之间的函数关系式;
(2)求t的取值范围;
(3)求3.5 s时小球的速度;
(4)求t(s)时小球的速度为16 m/s.
15.如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
数量/只 1 2 3 4 5 …
高度/cm 4 5.2 6.4 7.6 8.8 …
(1)上述两个变量之间的关系中,哪个是自变量?哪个是因变量?
(2)用 h(cm)表示这摞碗的高度,用 x(只)表示这摞碗的数量,请用含有 x 的代数式表示 h;
(3)若这摞碗的高度为 11.2cm,求这摞碗的数量.
五、综合题
16.随着科学技术的不断发展,电动汽车成为人们日常出行的重要交通工具,电动汽车的电池容量与续航里程成为人们最为关心的问题.现对某型号电动汽车充满电后进行测试,其电池剩余电量(度)与行驶里程(千米)之间的关系如下表所示:
行驶里程(千米) 0 10 20 40 …
剩余电量(度) 80 78 76 72 …
(1)表中自变量是________,因变量是__________.
(2)该型号电动汽车的电池容量为______度;
(3)请根据表中直接写出该电动汽车剩余电量(度)与行驶里程(千米)之间的关系式;
(4)求剩余电量为时电动汽车的行驶里程.
17.某市出租车采取分段收费方式:起步价为a元,即路程不超过b千米时收费a元,超过部分每千米收费c元乘车费与行驶路程之间的关系如图所示,请根据图象回答下列问题:
(1)由图象知, , , ;
(2)小明乘坐出租车行驶了23千米,那么他应付 元;
(3)若乘客乘坐出租车的路程为千米时,乘车费为y元,请求出y与x之间的关系式;
(4)若小明共付车费元,那么出租车共行驶 千米.
18.某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
六、实践探究题
19.如图,在中,点D是边的中点,点E是边上的一个动点,连接.设的面积为y,的长为x,小明对变量x和y之间的关系进行了探究,得到了如下的数据:
请根据以上信息,解答下列问题:
x 0 3 6
y 3 0 3
(1)题中的自变量和因变量分别是什么?当时,y的值是多少?直接写出的值;
(2)当的面积为面积的时,求出x的值.
答案解析部分
1.【答案】D
【知识点】常量、变量
2.【答案】D
【知识点】通过函数图象获取信息
3.【答案】B
【知识点】函数自变量的取值范围
4.【答案】A
【知识点】分式有无意义的条件;函数自变量的取值范围
5.【答案】A
【知识点】分式有无意义的条件;函数自变量的取值范围
6.【答案】90
【知识点】通过函数图象获取信息
7.【答案】
【知识点】函数自变量的取值范围
8.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
9.【答案】小寒
【知识点】通过函数图象获取信息
10.【答案】
【知识点】函数解析式
11.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
12.【答案】(1)(2)(3)9.8(4)2(5)
【知识点】通过函数图象获取信息
13.【答案】当x=-2时对应的函数值较大
【知识点】函数自变量的取值范围
14.【答案】(1)v=2t (2)0≤t≤20 (3)7cm/s (4)8s
【知识点】函数解析式;函数自变量的取值范围
15.【答案】(1)碗的数量是自变量,高度是因变量;
(2)h=1.2x+2.8;
(3)7只;
【知识点】函数的概念;函数解析式;函数自变量的取值范围
16.【答案】(1)行驶里程(千米);剩余电量(度)
(2)80
(3)
(4)300千米
【知识点】函数自变量的取值范围;用表格表示变量间的关系;用关系式表示变量间的关系
17.【答案】(1)8;3;
(2)38
(3)
(4)14
【知识点】函数自变量的取值范围;通过函数图象获取信息;用关系式表示变量间的关系
18.【答案】(1)解:第一天中,从4时到16时这头骆驼的体温是上升的,它的体温从最低上升到最高需要12小时.
(2)解:第三天12时这头骆驼的体温是39 ℃.
【知识点】通过函数图象获取信息
19.【答案】(1)自变量是的长,因变量是的面积;;
(2)或
【知识点】函数的概念;函数自变量的取值范围
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
