2.4 有理数的加法与减法 课件(4课时、共76张PPT) 2025-2026学年数学苏科版七年级上册
文档属性
| 名称 | 2.4 有理数的加法与减法 课件(4课时、共76张PPT) 2025-2026学年数学苏科版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览







文档简介
(共76张PPT)
第二章 有理数
2.4 有理数的加法与减法
第二章 有理数
2.4 课时1 有理数的加法
1.理解有理数加法的意义,掌握有理数加法的运算法则.
2.会进行有理数的加法运算.
3.会用有理数的加法解决简单实际问题.
问题 能否确定它现在位于原来位置的哪个方向,与原来位置相距多少米?
情境 1:若灰太狼在一条笔直的跑道上,先跑了20米,又跑了30米,我们规定向后为负,向前为正,即向前运动5米记作 5米,向后运动5米记作 -5米.
前
后
两次跑的方向不确定,最后位置也不确定
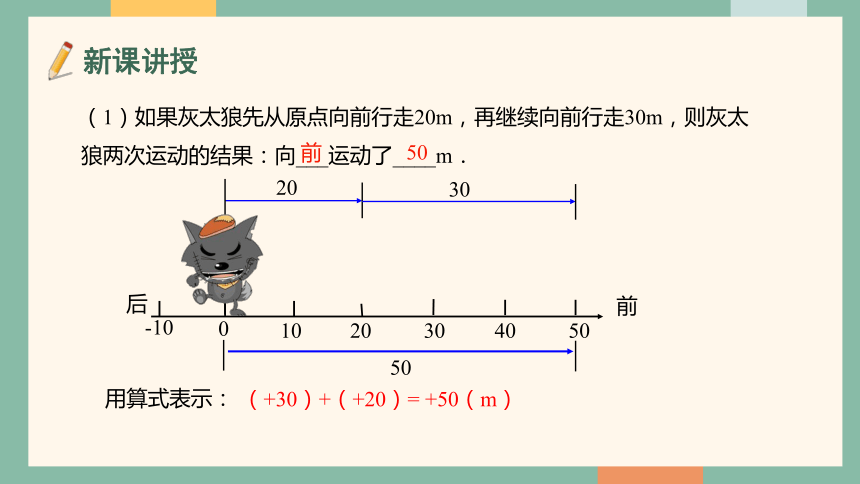
(1)如果灰太狼先从原点向前行走20m,再继续向前行走30m,则灰太狼两次运动的结果:向___运动了____m.
前
50
用算式表示:
(+30)+(+20)= +50(m)
0
10
20
30
40
50
20
30
50
前
后
-10
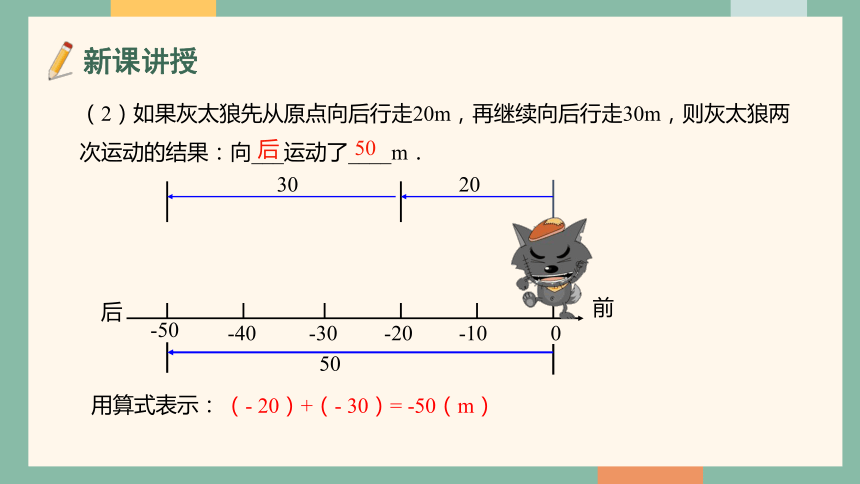
(2)如果灰太狼先从原点向后行走20m,再继续向后行走30m,则灰太狼两次运动的结果:向___运动了____m.
后
50
用算式表示:
(- 20)+(- 30)= -50(m)
-10
0
-20
-30
-40
-50
20
30
50
前
后
(3) 如果灰太狼先从原点向后行走20m,再向前行走20m,则灰太狼两次运动的结果:
用算式表示:
(- 20)+(+20)= 0(m)
初始位置
前
-10
10
30
20
-20
0
20
20
后
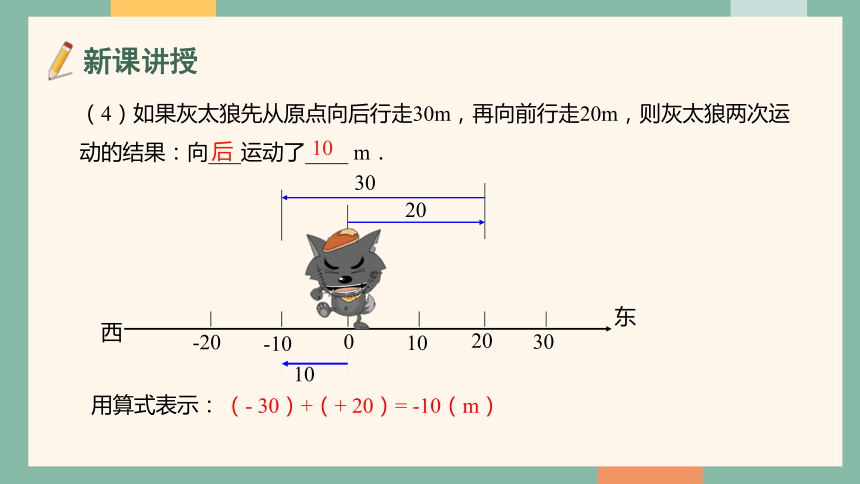
(4)如果灰太狼先从原点向后行走30m,再向前行走20m,则灰太狼两次运动的结果:向___运动了____ m.
后
10
用算式表示:
(- 30)+(+ 20)= -10(m)
东
-10
10
30
20
-20
0
20
30
10
西
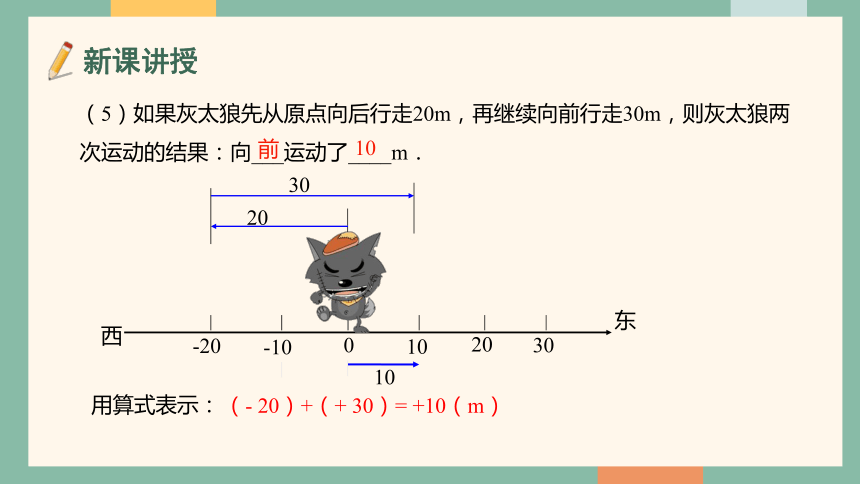
(5)如果灰太狼先从原点向后行走20m,再继续向前行走30m,则灰太狼两次运动的结果:向___运动了____m.
前
10
用算式表示:
(- 20)+(+ 30)= +10(m)
东
-10
10
30
20
-20
0
20
30
10
西
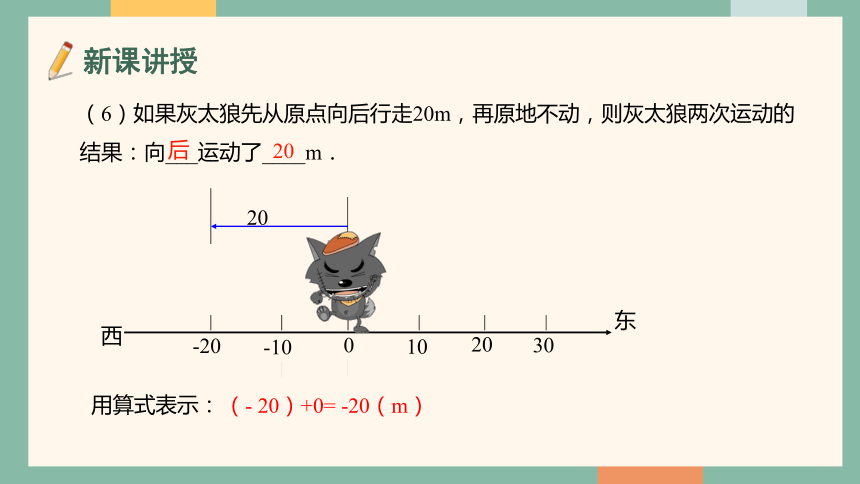
(6)如果灰太狼先从原点向后行走20m,再原地不动,则灰太狼两次运动的结果:向___运动了____m.
后
20
用算式表示:
(- 20)+0= -20(m)
东
-10
10
30
20
-20
0
20
西
观察下列算式和结果,与同桌交流并回答下列问题:
①(+20)+(+30)= +50 ; ②(- 20)+(- 30)= -50 ;
③(-20)+(+20)= 0; ④(-30) +(+20)=-10;
⑤(-20)+(+30)=+10; ⑥( -20)+0= -20.
(1)观察算式① ②,两个正数(或负数)相加时,怎样确定和的符号与和的绝对值?
两个正数相加,和的符号为正,和的绝对值等于加数的绝对值相加;两个负数相加,和的符号为负,和的绝对值等于加数的绝对值相加.
(2)观察算式③ ,一个正数和一个负数相加,绝对值相等时,和等于什么?
(3)观察算式④ ⑤ ,一个正数和一个负数相加,绝对值不相等时,怎样确定和的符号与和的绝对值?
(4)观察算式⑥ ,一个数同0相加,和等于什么?
③(-20)+(+20)= 0; ④(-30) +(+20)=-10;
⑤(-20)+(+30)=+10; ⑥( -20)+0= -20.
和等于0.
和的符号与绝对值较大加数的符号相同,和的绝对值等于较大加数的绝对值减去较小加数的绝对值.
和等于这个数.
归纳总结
有理数加法法则
(1)同号两数相加,和取相同符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时,和为0;绝对值不相等时,和取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值.
(3)一个数同0相加,仍得这个数.
例1:填表:
+
18+8
26
+
16-9
7
-
9+5
-14
归纳总结
有理数加法的运算步骤
例2:计算下列各题:
(1)(-4)+(-8); (2)(-5)+13;
(3) 0+(-7); (4)(-4.7)+4.7.
解:(1)(-4)+(-8)
=-(4+8)
=-12;
(2)(-5)+13=+(13-5)=8;
(3)0+(-7)=-7;
(4)(-4.7)+4.7=-4.7+4.7=0.
例3:2020年11月10日,中国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底,坐底深度为10 909 m.海平面的高度为0 m.潜水器坐底成功后顺利返航,当从坐底位置上升3 000 m时,求潜水器相对于海平面的位置.
解:潜水器下潜10 909 m,记作-10 909 m;上升3 000 m,记作+3 000 m.
根据题意,得(-10 909)+(+3 000)=-(10 909-3 000)=-7 909(m).
答:当从坐底位置上升3 000 m时,求潜水器相对于海平面下7 909 m处.
1.计算(-3)+5的结果等于( )
A.2 B.-2 C.8 D.-8
2.两个数的和为正数,那么这两个数是( )
A.正数 B.负数 C.一正一负 D.至少一个为正数
A
D
3.中 岳 嵩 山,是 我 国 著 名 的 五 岳之一,位 于 河 南 省 郑 州 市 登 封 市 . 已 知 嵩 山 山顶某日早 晨 的 气 温是 -2 ℃,到中午上升了 10 ℃,则 这 天 中 午 嵩 山 山 顶 的 气 温是( )
A. -12℃ B. -8℃ C. 8℃ D. 10℃
C
4.有理数a、b在数轴上的位置如图所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
A
-1
a
0
1
b
有理数的加法
有理数的加法法则
有理数加法的实际运用
同号两数相加,和取相同符号,并把绝对值相加.
异号两数相加,绝对值相等时,和为0;绝对值不相等时,和取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
一个数同0相加,仍得这个数.
第2章 有理数
2.4 课时2 有理数的加法运算律
1.理解有理数的加法运算律,并能灵活运用,简化运算.
2.能运用有理数的加法解决实际问题.
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 取相同符号
取绝对值较大的
加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则
(1)(-8)+(-9)= _____, (-9)+(-8)=______;
(2)4+(-7)=______ , (-7)+4=______;
(3)[2+(-3)]+(-8)= ______,
2+[(-3)+(-8)]= ______;
(4)10+[(-10)+(-5)] = _______ ,
[10+(-10)]+(-5)=________.
完成下列计算.
-17
-17
-3
-3
-9
-9
-5
-5
仔细观察上述计算,你发现了什么?
在有理数的范围内,加法的交换律与结合律仍然适用.
归纳总结
(1)加法交换律:两个数相加,交换加数的位置,和不变
a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加再和第三个数相加,或先把后两个数相加再和第一个数相加,和不变
(a+b)+c=a+(b+c)
例1:计算:(1)16+(-25)+24+(-32);(2)31 +(-28)+ 28 + 69;
(3)(-2.48)+4.33+(-7.52)+(-4.33);(4)
解:(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32) (加法交换律)
=(16+24)+[(-25)+(-32)] (加法结合律)
=40+(-57 ) (同号相加法则)
=-17. (异号相加法则)
(2)31 +(-28)+ 28 + 69;
(3)(-2.48)+4.33+(-7.52)+(-4.33);(4)
(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100.
(3)原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10.
(4)
(4)原式
归纳总结
应用加法运算律运算时常用的三个规律:
1.一般地,总是先把正数或负数分别结合在一起相加.
2.有相反数的可先把相反数相加,能凑整的可先凑整.
3.有分母相同的,可先把分母相同的数结合相加.
例2:某股民以每股38.5元的价格持有某种股票.下表为一周内该股票的涨跌情况:
时间 星期一 星期二 星期三 星期四 星期五
每股涨跌/元 -1.8 +0.6 +1.5 -0.2 +0.4
在星期五收盘时,该股票的价格是多少元?
解:根据题意,得38.5+(-1.8)+(+0.6)+(+1.5)+(-0.2)+(+0.4)
=38.5+(+1.5)+(-1.8)+(-0.2)+(+0.6)+(+0.4)
=[38.5+(+1.5)]+[(-1.8)+(-0.2)]+[(+0.6)+(+0.4)]
=[40+(-2)]+(+1)
=38+(+1)
=39(元).
答:在星期五收盘时,该股票的价格是39元.
时间 星期一 星期二 星期三 星期四 星期五
每股涨跌/元 -1.8 +0.6 +1.5 -0.2 +0.4
例3:10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5. 问这10筐苹果总共重多少千克?
=4
总重量为:30×10+4=304(千克)
=8+(-4)+0+0
解:根据题意得:2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
答:这10筐苹果总重量为304千克.
1.下列运算中正确的是( )
A.8+[14+(-9)]=15
B.(-2.5)+[5+(-2.5)]=5
C.[3+(-3)]+(-2)=-2
D.3.14+[(-8)+3.14]=-8
C
2.某储蓄所先后办理了7笔业务:取出9.5万元,存入5万元,取出8万元,存入12万元,存入25万元,取出10.25万元,取出2万元,这时的存款比最初( )
A.增加12.25万元 B.减少12.25万元
C.增加12万元 D.减少12万元
A
3.用简便方法计算:
(1)(+23)+(- 27)+(+ 9)+(- 5);
(2)(+0.7)+(- 0.9)+(- 1.8)+ 1.3 +(- 0.2).
解:(1)原式 =[( + 23 ) + ( + 9 )]+[( - 27 ) + ( - 5 )]
= ( + 32 ) + ( - 32 )
= 0.
(2)原式 =[( + 0.7 ) + 1.3]+[( - 1.8 ) + ( - 0.2 )]+ ( - 0.9 )
= 2 + ( - 2 ) + ( - 0.9 )
= - 0.9.
有理数加法运算律
加法交换律:a+b=b+a
加法结合律:
(a+b)+c=a+(b+c)
简化运算
第2章 有理数
2.4 课时3 有理数的减法
1.会正确进行有理数的减法运算.
2.会利用有理数的减法运算解决简单的实际问题.
(1) 1 + 6=
(2)(–2)+(–8)=
(3)(–9)+10=
(4) 5 + (–9)=
(5)(–2.2)+ 2.2=
(6) 6 + 0 =
(7) 0 + (–8)=
7
–10
1
–4
6
–8
0
计算:
有理数的减法怎么计算呢?
下表是中央气象台发布的某日天气预报中部分城市的最高气温和最低气温的统计表.
城 市 最高气温(℃) 最低气温(℃)
昆 明 16 5
沈 阳 -9 -16
北 京 -1 -9
(1)分别填写表示各城市温差的算式以及从温度计上的刻度观察到的温差.
城 市 表示温差的算式 观察到的温差(℃)
昆 明 16-5
沈 阳 -9-(-16)
北 京 (-1)-(-9)
(1)分别填写表示各城市温差的算式以及从温度计上的刻度观察到的温差.
11
7
8
(2)表示温差的算式与观察到的温差之间有什么关系?
表示温差的算式结果与观察到的温差相等
(3)-9-(-16)=7,另一方面-9+(+16)= .
7
由上面的式子可知
-9-(-16)=-9+(+16)
问题:计算下面各式,验证前面的规律是否成立.
0 - ( - 3 ) = _ __, 0 + ( + 3 ) = _ __;
1 - ( - 3 ) = _ __, 1+ ( + 3 ) = _ __;
- 5 - ( - 3 ) =_ __, - 5 + ( + 3 ) = _ .
3
- 2
4
- 2
4
3
归纳总结
有理数减法法则
减去一个数,等于加上这个数的相反数
用字母表示成一般形式:a-b=a+(-b)
注意:减法在运算时有2个要素要发生变化
加号
减号
相反数
减数
法则适用于任何两
个有理数相减
例1:计算下列各题:
(1) 7-3; (2) 3-7; (3)(-1) -2;(4) 2- (-1);
(5)(-2) -(-1); (6)(-1) -(-2);(7) 0-5; (8) 0- (-5) .
解:(1) 7-3 =4.
(2)3-7 =3+(- 7) = - 4.
(3)(-1) -2 =(- 1) +(- 2) = - 3.
(4)2- (-1) =2+1=3.
交换被减数与减数的位
置,差互为相反数.
(5)(-2) -(-1); (6)(-1) -(-2);(7) 0-5; (8) 0- (-5) .
(5)(-2) -(-1)= (-2) +1= - 1.
(6)(-1) -(-2) = (-1) +2=1.
(7)0-5=0+( - 5) = - 5.
0减去一个数,结果等
于这个数的相反数.
(8)0- (-5) =0+5=5.
例2:计算:
(1)5+(-3)-(-2);
(2)(-5)-(-2.4)+(-1).
解:(1) 5+(-3)-(-2)=5+(-3)+2=4.
(2)(-5)-(-2.4)+(-1)=(-5)+2.4+(-1)=-3.6.
例3:我国航天科技飞速发展,2019年1月3日,嫦娥四号探测器成功着陆月球背面,实现了人类探测器首次在月球背面软着陆.研究表明:月球表面最高温度约为160℃,最低温度约为-180℃,月球表面的温差约为多少摄氏度?
解:160-(-180)=160+180=340℃,
故月球表面的温差约为340摄氏度.
例4:某矿井的剖面示意图如图所示,以地面为准,点 A的高度是3 m, B, C, D三点的高度分别是-10 m, -20 m,-30 m.
(1) A, B, C, D 四个点中,最低点比最高点低多少米?
(2)点 B 比点 D 高多少米?
解:(1)由图可知,点 A 是最高点,点 D 是最低点,
所以 3- (-30) =3+(+30) =33(m),
即最低点比最高点低 33 m.
例4:某矿井的剖面示意图如图所示,以地面为准,点 A的高度是3 m, B, C, D三点的高度分别是-10 m, -20 m,-30 m.
(2)点 B 比点 D 高多少米?
(2)(-10) -(-30) =(-10) +(+30) =20(m),
故点 B 比点 D 高 20 m.
1.下列算式中正确的有( )
①2-(-2)=0;②(-3)-(+3)=0;③(-3)-|-3|=0;④0-(-1)=1.
A.1个 B.2个 C.3个 D.4个
A
2.“早穿棉袄午穿纱,围着火炉吃西 瓜”是 对 新疆地区昼夜温差的真实写照 . 据统计,吐鲁番三月份某天的最高气温是 27 ℃ ,最低气 温 是 -1 ℃ ,则吐鲁番这天的温差(最 高气温与最低气温的差)为( )
A. 26℃ B. 27℃
C. 28℃ D. 29℃
C
3.判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大.( )
(2)两个数相减,被减数一定比减数大.( )
(3)两数之差一定小于被减数.( )
(4)0减去任何数,差都为负数.( )
(5)较大的数减去较小的数,差一定是正数.( )
√
×
×
×
×
(1)(-3)―(―5);(2)0-7;(3)7.2―(―4.8);(4)-3 .
-5
解:(1) (-3)―(―5)= (-3)+5=2;
4.计算:
(2) 0-7 = 0+(-7) =-7;
(3) 7.2―(―4.8) = 7.2+4.8 = 12;
(4) -3 -5 =-3 +( -5 )=-8
5.某工厂在2023年第一季度效益如下:一月份获利150万元,二月份比一月份少获利70万元,三月份亏损5万元,则一月份比三月份多获利________万元,该工厂第一季度共获利________万元.
225
155
减法
加法
“—”变“+”
减数变成相反数
转化思想
第2章 有理数
2.4 课时4 有理数的加减混合运算
1.会进行有理数的加减混合运算,并能用运算律简化计算.
2.能综合运用有理数的加减法的相关知识解决简单的实际问题.
有理数的加法法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两数相加等于0.
3.一个数同0相加,仍得这个数.
有理数减法法则
减去一个数等于加这个数的相反数
根据所学知识,试着解决问题.
北京冬奥会的开幕式于2022年2月4日在国家体育场举行.当日,北京市的最低气温是-6℃,北京冬奥会张家口赛区位于张家口市崇礼区,该地当日的最低气温是-21℃,最高气温是-11℃,并且张家口市崇礼区的温差比北京市的温差大3℃.
(1)张家口市崇礼区当日的温差是多少摄氏度?
(2)北京市当日的温差是多少摄氏度?
(3)北京市当日的最高气温是多少摄氏度?
-11-(-21)=10℃
10-3=7℃
7+(-6)=1℃
北京市的最高气温可以用下面的方式直接求出:
(-11)-(-21)-(+3)+(-6)
分析:这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为
(-11)-(-21)-(+3)+(-6)
=(-11)+(+21)+(-3)+(-6)
使问题转化为几个有理数的加法.
=1(℃)
表示-11、+21、-3、-6的和
归纳总结
在有理数的加减混合运算中,把加减混合运算都统一成加法运算,原来的算式就转化为求几个正数或负数的和.
在一个算式里,通常把各个加数的括号及其前面的运算符号“+”省略不写.
如(-11)+(+21)+(-3)+(-6)可写成-11+21-3-6.
读作负11、正21、负3与负6的和
读作负11加21减3减6
例1:把下列各式写成省略加号和括号的形式,并写出它们的两种读法 .
(1) - 6 -(- 3)+(- 2) -(+6) -(- 7);
(2) - + (- )- (- ) +( - ) - (- ).
解:(1) - 6 -(- 3)+(- 2) -(+6) -(- 7) = - 6+3 - 2 - 6+7.
读法一:负 6,正 3,负 2,负 6 与正 7 的和;
读法二:负 6 加 3 减 2 减 6 加 7.
(2)- + (- )- (- ) +( - ) - (- )= - - + - + .
读法一:负 ,负 ,正 ,负 与正 的和;
读法二:负 减 加 减 加 .
例1:把下列各式写成省略加号和括号的形式,并写出它们的两种读法 .
(2) - + (- )- (- ) +( - ) - (- ).
例2:计算:
(1)2.7+(- 8.5) -(+3.4) -(- 1.2);(2) - 0.6 - 0.08+ - 2 - 0.92+2 .
解:(1)2.7+(- 8.5) -(+3.4) -(- 1.2)
=2.7-8.5-3.4+1.2
=(2.7+1.2) +(-8.5-3.4)
=3.9-11.9
=-8.
同号结合法
(2) - 0.6 - 0.08+ - 2 - 0.92+2 .
(2) - 0.6 - 0.08+ - 2 - 0.92+2
=(- 0.6+0.4)+( - 0.08 - 0.92) +(- 2 +2 )
= - 0.2 - 1+0
= - 1.2.
①凑整法;
②相反数结合法.
归纳总结
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
注意:
(1)运用加法交换律交换加数的位置时,要连同前面的符号一起交换;
(2)运用加法结合律时,把同号的加数结合、同分母的加数结合、便于通分的加数结合、能凑成整数的加数结合、互为相反数的加数结合,都可以使运算简化 .
例3:某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上几班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数):
(1)本周三生产了多少辆摩托车?
解:(1)300 -3=297(辆).
答:本周三生产了297辆摩托车.
(2)-5+7-3+4+10-9-25=-21(辆).
答:本周总生产量与计划量相比减少了21辆.
(2)本周总生产量与计划量相比,是增加还是减少了?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
(3)10-(-25)=35(辆).
答:产量最多的一天比产量最少的一天多生产了35辆.
1.下列式子不可读作“负 1,负 3,正 6 与负 8 的和”的是( )
A. - 1 - 3+6 - 8
B. - 1+(- 3) +(- 6) -(- 8)
C. - 1 -(+3) +(+6) +(- 8)
D. -(+1) - 3 -(- 6) +(- 8)
B
2.把6-(+3)-(-7)+(-2)中的减法改成加法,并写成省略加号和括号的形式为( )
A.-6-3+7-2 B.6-3-7-2
C.6-3+7-2 D.6+3-7-2
C
3.某潜艇在海平面以下36米处上升(下潜)情况如下表(上升为正,下潜为负):
第1次 第2次 第3次 第4次 第5次
上升(下潜) +10米 -5米 -10米 +12米 -8米
第四次上升后,在( )
A.海平面以下29米 B.海平面以下31米
C 海平面以下41米 D.海平面以下26米
A
4.计算:
(1)0-(+8)+(-2.7)-(+1.3);
(2)-3.92+6.24-8.56+4.28;
解:(1)原式=-8+(-2.7)+(-1.3)
=-8+[(-2.7)+(-1.3)]
=-8+(-4)
=-12
(2)原式=-3.92-8.56+6.24+4.28
=-(3.92+8.56)+(6.24+4.28)
=-12.48+10.52
=-1.96
(3)
(4)
(3) (4)
(3)原式
(4)原式
有理数的加减混合运算
加减混合算式的读法与写法
有理数的加减混合运算
有理数的加减混合运算的应用
第二章 有理数
2.4 有理数的加法与减法
第二章 有理数
2.4 课时1 有理数的加法
1.理解有理数加法的意义,掌握有理数加法的运算法则.
2.会进行有理数的加法运算.
3.会用有理数的加法解决简单实际问题.
问题 能否确定它现在位于原来位置的哪个方向,与原来位置相距多少米?
情境 1:若灰太狼在一条笔直的跑道上,先跑了20米,又跑了30米,我们规定向后为负,向前为正,即向前运动5米记作 5米,向后运动5米记作 -5米.
前
后
两次跑的方向不确定,最后位置也不确定
(1)如果灰太狼先从原点向前行走20m,再继续向前行走30m,则灰太狼两次运动的结果:向___运动了____m.
前
50
用算式表示:
(+30)+(+20)= +50(m)
0
10
20
30
40
50
20
30
50
前
后
-10
(2)如果灰太狼先从原点向后行走20m,再继续向后行走30m,则灰太狼两次运动的结果:向___运动了____m.
后
50
用算式表示:
(- 20)+(- 30)= -50(m)
-10
0
-20
-30
-40
-50
20
30
50
前
后
(3) 如果灰太狼先从原点向后行走20m,再向前行走20m,则灰太狼两次运动的结果:
用算式表示:
(- 20)+(+20)= 0(m)
初始位置
前
-10
10
30
20
-20
0
20
20
后
(4)如果灰太狼先从原点向后行走30m,再向前行走20m,则灰太狼两次运动的结果:向___运动了____ m.
后
10
用算式表示:
(- 30)+(+ 20)= -10(m)
东
-10
10
30
20
-20
0
20
30
10
西
(5)如果灰太狼先从原点向后行走20m,再继续向前行走30m,则灰太狼两次运动的结果:向___运动了____m.
前
10
用算式表示:
(- 20)+(+ 30)= +10(m)
东
-10
10
30
20
-20
0
20
30
10
西
(6)如果灰太狼先从原点向后行走20m,再原地不动,则灰太狼两次运动的结果:向___运动了____m.
后
20
用算式表示:
(- 20)+0= -20(m)
东
-10
10
30
20
-20
0
20
西
观察下列算式和结果,与同桌交流并回答下列问题:
①(+20)+(+30)= +50 ; ②(- 20)+(- 30)= -50 ;
③(-20)+(+20)= 0; ④(-30) +(+20)=-10;
⑤(-20)+(+30)=+10; ⑥( -20)+0= -20.
(1)观察算式① ②,两个正数(或负数)相加时,怎样确定和的符号与和的绝对值?
两个正数相加,和的符号为正,和的绝对值等于加数的绝对值相加;两个负数相加,和的符号为负,和的绝对值等于加数的绝对值相加.
(2)观察算式③ ,一个正数和一个负数相加,绝对值相等时,和等于什么?
(3)观察算式④ ⑤ ,一个正数和一个负数相加,绝对值不相等时,怎样确定和的符号与和的绝对值?
(4)观察算式⑥ ,一个数同0相加,和等于什么?
③(-20)+(+20)= 0; ④(-30) +(+20)=-10;
⑤(-20)+(+30)=+10; ⑥( -20)+0= -20.
和等于0.
和的符号与绝对值较大加数的符号相同,和的绝对值等于较大加数的绝对值减去较小加数的绝对值.
和等于这个数.
归纳总结
有理数加法法则
(1)同号两数相加,和取相同符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时,和为0;绝对值不相等时,和取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值.
(3)一个数同0相加,仍得这个数.
例1:填表:
+
18+8
26
+
16-9
7
-
9+5
-14
归纳总结
有理数加法的运算步骤
例2:计算下列各题:
(1)(-4)+(-8); (2)(-5)+13;
(3) 0+(-7); (4)(-4.7)+4.7.
解:(1)(-4)+(-8)
=-(4+8)
=-12;
(2)(-5)+13=+(13-5)=8;
(3)0+(-7)=-7;
(4)(-4.7)+4.7=-4.7+4.7=0.
例3:2020年11月10日,中国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底,坐底深度为10 909 m.海平面的高度为0 m.潜水器坐底成功后顺利返航,当从坐底位置上升3 000 m时,求潜水器相对于海平面的位置.
解:潜水器下潜10 909 m,记作-10 909 m;上升3 000 m,记作+3 000 m.
根据题意,得(-10 909)+(+3 000)=-(10 909-3 000)=-7 909(m).
答:当从坐底位置上升3 000 m时,求潜水器相对于海平面下7 909 m处.
1.计算(-3)+5的结果等于( )
A.2 B.-2 C.8 D.-8
2.两个数的和为正数,那么这两个数是( )
A.正数 B.负数 C.一正一负 D.至少一个为正数
A
D
3.中 岳 嵩 山,是 我 国 著 名 的 五 岳之一,位 于 河 南 省 郑 州 市 登 封 市 . 已 知 嵩 山 山顶某日早 晨 的 气 温是 -2 ℃,到中午上升了 10 ℃,则 这 天 中 午 嵩 山 山 顶 的 气 温是( )
A. -12℃ B. -8℃ C. 8℃ D. 10℃
C
4.有理数a、b在数轴上的位置如图所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
A
-1
a
0
1
b
有理数的加法
有理数的加法法则
有理数加法的实际运用
同号两数相加,和取相同符号,并把绝对值相加.
异号两数相加,绝对值相等时,和为0;绝对值不相等时,和取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
一个数同0相加,仍得这个数.
第2章 有理数
2.4 课时2 有理数的加法运算律
1.理解有理数的加法运算律,并能灵活运用,简化运算.
2.能运用有理数的加法解决实际问题.
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 取相同符号
取绝对值较大的
加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则
(1)(-8)+(-9)= _____, (-9)+(-8)=______;
(2)4+(-7)=______ , (-7)+4=______;
(3)[2+(-3)]+(-8)= ______,
2+[(-3)+(-8)]= ______;
(4)10+[(-10)+(-5)] = _______ ,
[10+(-10)]+(-5)=________.
完成下列计算.
-17
-17
-3
-3
-9
-9
-5
-5
仔细观察上述计算,你发现了什么?
在有理数的范围内,加法的交换律与结合律仍然适用.
归纳总结
(1)加法交换律:两个数相加,交换加数的位置,和不变
a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加再和第三个数相加,或先把后两个数相加再和第一个数相加,和不变
(a+b)+c=a+(b+c)
例1:计算:(1)16+(-25)+24+(-32);(2)31 +(-28)+ 28 + 69;
(3)(-2.48)+4.33+(-7.52)+(-4.33);(4)
解:(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32) (加法交换律)
=(16+24)+[(-25)+(-32)] (加法结合律)
=40+(-57 ) (同号相加法则)
=-17. (异号相加法则)
(2)31 +(-28)+ 28 + 69;
(3)(-2.48)+4.33+(-7.52)+(-4.33);(4)
(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100.
(3)原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10.
(4)
(4)原式
归纳总结
应用加法运算律运算时常用的三个规律:
1.一般地,总是先把正数或负数分别结合在一起相加.
2.有相反数的可先把相反数相加,能凑整的可先凑整.
3.有分母相同的,可先把分母相同的数结合相加.
例2:某股民以每股38.5元的价格持有某种股票.下表为一周内该股票的涨跌情况:
时间 星期一 星期二 星期三 星期四 星期五
每股涨跌/元 -1.8 +0.6 +1.5 -0.2 +0.4
在星期五收盘时,该股票的价格是多少元?
解:根据题意,得38.5+(-1.8)+(+0.6)+(+1.5)+(-0.2)+(+0.4)
=38.5+(+1.5)+(-1.8)+(-0.2)+(+0.6)+(+0.4)
=[38.5+(+1.5)]+[(-1.8)+(-0.2)]+[(+0.6)+(+0.4)]
=[40+(-2)]+(+1)
=38+(+1)
=39(元).
答:在星期五收盘时,该股票的价格是39元.
时间 星期一 星期二 星期三 星期四 星期五
每股涨跌/元 -1.8 +0.6 +1.5 -0.2 +0.4
例3:10筐苹果,以每筐30千克为基准,超过的千克数记作正数,不足的千克数记作负数,记录如下:2, -4, 2.5, 3, -0.5, 1.5, 3, -1, 0, -2.5. 问这10筐苹果总共重多少千克?
=4
总重量为:30×10+4=304(千克)
=8+(-4)+0+0
解:根据题意得:2+(-4)+2.5+3+(-0.5)+1.5+3+(-1)+0+(-2.5)
=(2+3+3)+(-4)+[2.5+(-2.5)]+[(-0.5)+(-1)+1.5]
答:这10筐苹果总重量为304千克.
1.下列运算中正确的是( )
A.8+[14+(-9)]=15
B.(-2.5)+[5+(-2.5)]=5
C.[3+(-3)]+(-2)=-2
D.3.14+[(-8)+3.14]=-8
C
2.某储蓄所先后办理了7笔业务:取出9.5万元,存入5万元,取出8万元,存入12万元,存入25万元,取出10.25万元,取出2万元,这时的存款比最初( )
A.增加12.25万元 B.减少12.25万元
C.增加12万元 D.减少12万元
A
3.用简便方法计算:
(1)(+23)+(- 27)+(+ 9)+(- 5);
(2)(+0.7)+(- 0.9)+(- 1.8)+ 1.3 +(- 0.2).
解:(1)原式 =[( + 23 ) + ( + 9 )]+[( - 27 ) + ( - 5 )]
= ( + 32 ) + ( - 32 )
= 0.
(2)原式 =[( + 0.7 ) + 1.3]+[( - 1.8 ) + ( - 0.2 )]+ ( - 0.9 )
= 2 + ( - 2 ) + ( - 0.9 )
= - 0.9.
有理数加法运算律
加法交换律:a+b=b+a
加法结合律:
(a+b)+c=a+(b+c)
简化运算
第2章 有理数
2.4 课时3 有理数的减法
1.会正确进行有理数的减法运算.
2.会利用有理数的减法运算解决简单的实际问题.
(1) 1 + 6=
(2)(–2)+(–8)=
(3)(–9)+10=
(4) 5 + (–9)=
(5)(–2.2)+ 2.2=
(6) 6 + 0 =
(7) 0 + (–8)=
7
–10
1
–4
6
–8
0
计算:
有理数的减法怎么计算呢?
下表是中央气象台发布的某日天气预报中部分城市的最高气温和最低气温的统计表.
城 市 最高气温(℃) 最低气温(℃)
昆 明 16 5
沈 阳 -9 -16
北 京 -1 -9
(1)分别填写表示各城市温差的算式以及从温度计上的刻度观察到的温差.
城 市 表示温差的算式 观察到的温差(℃)
昆 明 16-5
沈 阳 -9-(-16)
北 京 (-1)-(-9)
(1)分别填写表示各城市温差的算式以及从温度计上的刻度观察到的温差.
11
7
8
(2)表示温差的算式与观察到的温差之间有什么关系?
表示温差的算式结果与观察到的温差相等
(3)-9-(-16)=7,另一方面-9+(+16)= .
7
由上面的式子可知
-9-(-16)=-9+(+16)
问题:计算下面各式,验证前面的规律是否成立.
0 - ( - 3 ) = _ __, 0 + ( + 3 ) = _ __;
1 - ( - 3 ) = _ __, 1+ ( + 3 ) = _ __;
- 5 - ( - 3 ) =_ __, - 5 + ( + 3 ) = _ .
3
- 2
4
- 2
4
3
归纳总结
有理数减法法则
减去一个数,等于加上这个数的相反数
用字母表示成一般形式:a-b=a+(-b)
注意:减法在运算时有2个要素要发生变化
加号
减号
相反数
减数
法则适用于任何两
个有理数相减
例1:计算下列各题:
(1) 7-3; (2) 3-7; (3)(-1) -2;(4) 2- (-1);
(5)(-2) -(-1); (6)(-1) -(-2);(7) 0-5; (8) 0- (-5) .
解:(1) 7-3 =4.
(2)3-7 =3+(- 7) = - 4.
(3)(-1) -2 =(- 1) +(- 2) = - 3.
(4)2- (-1) =2+1=3.
交换被减数与减数的位
置,差互为相反数.
(5)(-2) -(-1); (6)(-1) -(-2);(7) 0-5; (8) 0- (-5) .
(5)(-2) -(-1)= (-2) +1= - 1.
(6)(-1) -(-2) = (-1) +2=1.
(7)0-5=0+( - 5) = - 5.
0减去一个数,结果等
于这个数的相反数.
(8)0- (-5) =0+5=5.
例2:计算:
(1)5+(-3)-(-2);
(2)(-5)-(-2.4)+(-1).
解:(1) 5+(-3)-(-2)=5+(-3)+2=4.
(2)(-5)-(-2.4)+(-1)=(-5)+2.4+(-1)=-3.6.
例3:我国航天科技飞速发展,2019年1月3日,嫦娥四号探测器成功着陆月球背面,实现了人类探测器首次在月球背面软着陆.研究表明:月球表面最高温度约为160℃,最低温度约为-180℃,月球表面的温差约为多少摄氏度?
解:160-(-180)=160+180=340℃,
故月球表面的温差约为340摄氏度.
例4:某矿井的剖面示意图如图所示,以地面为准,点 A的高度是3 m, B, C, D三点的高度分别是-10 m, -20 m,-30 m.
(1) A, B, C, D 四个点中,最低点比最高点低多少米?
(2)点 B 比点 D 高多少米?
解:(1)由图可知,点 A 是最高点,点 D 是最低点,
所以 3- (-30) =3+(+30) =33(m),
即最低点比最高点低 33 m.
例4:某矿井的剖面示意图如图所示,以地面为准,点 A的高度是3 m, B, C, D三点的高度分别是-10 m, -20 m,-30 m.
(2)点 B 比点 D 高多少米?
(2)(-10) -(-30) =(-10) +(+30) =20(m),
故点 B 比点 D 高 20 m.
1.下列算式中正确的有( )
①2-(-2)=0;②(-3)-(+3)=0;③(-3)-|-3|=0;④0-(-1)=1.
A.1个 B.2个 C.3个 D.4个
A
2.“早穿棉袄午穿纱,围着火炉吃西 瓜”是 对 新疆地区昼夜温差的真实写照 . 据统计,吐鲁番三月份某天的最高气温是 27 ℃ ,最低气 温 是 -1 ℃ ,则吐鲁番这天的温差(最 高气温与最低气温的差)为( )
A. 26℃ B. 27℃
C. 28℃ D. 29℃
C
3.判断并说明理由
(1)在有理数的加法中,两数的和一定比加数大.( )
(2)两个数相减,被减数一定比减数大.( )
(3)两数之差一定小于被减数.( )
(4)0减去任何数,差都为负数.( )
(5)较大的数减去较小的数,差一定是正数.( )
√
×
×
×
×
(1)(-3)―(―5);(2)0-7;(3)7.2―(―4.8);(4)-3 .
-5
解:(1) (-3)―(―5)= (-3)+5=2;
4.计算:
(2) 0-7 = 0+(-7) =-7;
(3) 7.2―(―4.8) = 7.2+4.8 = 12;
(4) -3 -5 =-3 +( -5 )=-8
5.某工厂在2023年第一季度效益如下:一月份获利150万元,二月份比一月份少获利70万元,三月份亏损5万元,则一月份比三月份多获利________万元,该工厂第一季度共获利________万元.
225
155
减法
加法
“—”变“+”
减数变成相反数
转化思想
第2章 有理数
2.4 课时4 有理数的加减混合运算
1.会进行有理数的加减混合运算,并能用运算律简化计算.
2.能综合运用有理数的加减法的相关知识解决简单的实际问题.
有理数的加法法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两数相加等于0.
3.一个数同0相加,仍得这个数.
有理数减法法则
减去一个数等于加这个数的相反数
根据所学知识,试着解决问题.
北京冬奥会的开幕式于2022年2月4日在国家体育场举行.当日,北京市的最低气温是-6℃,北京冬奥会张家口赛区位于张家口市崇礼区,该地当日的最低气温是-21℃,最高气温是-11℃,并且张家口市崇礼区的温差比北京市的温差大3℃.
(1)张家口市崇礼区当日的温差是多少摄氏度?
(2)北京市当日的温差是多少摄氏度?
(3)北京市当日的最高气温是多少摄氏度?
-11-(-21)=10℃
10-3=7℃
7+(-6)=1℃
北京市的最高气温可以用下面的方式直接求出:
(-11)-(-21)-(+3)+(-6)
分析:这个算式中有加法,也有减法.可以根据有理数减法法则,把它改写为
(-11)-(-21)-(+3)+(-6)
=(-11)+(+21)+(-3)+(-6)
使问题转化为几个有理数的加法.
=1(℃)
表示-11、+21、-3、-6的和
归纳总结
在有理数的加减混合运算中,把加减混合运算都统一成加法运算,原来的算式就转化为求几个正数或负数的和.
在一个算式里,通常把各个加数的括号及其前面的运算符号“+”省略不写.
如(-11)+(+21)+(-3)+(-6)可写成-11+21-3-6.
读作负11、正21、负3与负6的和
读作负11加21减3减6
例1:把下列各式写成省略加号和括号的形式,并写出它们的两种读法 .
(1) - 6 -(- 3)+(- 2) -(+6) -(- 7);
(2) - + (- )- (- ) +( - ) - (- ).
解:(1) - 6 -(- 3)+(- 2) -(+6) -(- 7) = - 6+3 - 2 - 6+7.
读法一:负 6,正 3,负 2,负 6 与正 7 的和;
读法二:负 6 加 3 减 2 减 6 加 7.
(2)- + (- )- (- ) +( - ) - (- )= - - + - + .
读法一:负 ,负 ,正 ,负 与正 的和;
读法二:负 减 加 减 加 .
例1:把下列各式写成省略加号和括号的形式,并写出它们的两种读法 .
(2) - + (- )- (- ) +( - ) - (- ).
例2:计算:
(1)2.7+(- 8.5) -(+3.4) -(- 1.2);(2) - 0.6 - 0.08+ - 2 - 0.92+2 .
解:(1)2.7+(- 8.5) -(+3.4) -(- 1.2)
=2.7-8.5-3.4+1.2
=(2.7+1.2) +(-8.5-3.4)
=3.9-11.9
=-8.
同号结合法
(2) - 0.6 - 0.08+ - 2 - 0.92+2 .
(2) - 0.6 - 0.08+ - 2 - 0.92+2
=(- 0.6+0.4)+( - 0.08 - 0.92) +(- 2 +2 )
= - 0.2 - 1+0
= - 1.2.
①凑整法;
②相反数结合法.
归纳总结
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
注意:
(1)运用加法交换律交换加数的位置时,要连同前面的符号一起交换;
(2)运用加法结合律时,把同号的加数结合、同分母的加数结合、便于通分的加数结合、能凑成整数的加数结合、互为相反数的加数结合,都可以使运算简化 .
例3:某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上几班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数):
(1)本周三生产了多少辆摩托车?
解:(1)300 -3=297(辆).
答:本周三生产了297辆摩托车.
(2)-5+7-3+4+10-9-25=-21(辆).
答:本周总生产量与计划量相比减少了21辆.
(2)本周总生产量与计划量相比,是增加还是减少了?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
(3)10-(-25)=35(辆).
答:产量最多的一天比产量最少的一天多生产了35辆.
1.下列式子不可读作“负 1,负 3,正 6 与负 8 的和”的是( )
A. - 1 - 3+6 - 8
B. - 1+(- 3) +(- 6) -(- 8)
C. - 1 -(+3) +(+6) +(- 8)
D. -(+1) - 3 -(- 6) +(- 8)
B
2.把6-(+3)-(-7)+(-2)中的减法改成加法,并写成省略加号和括号的形式为( )
A.-6-3+7-2 B.6-3-7-2
C.6-3+7-2 D.6+3-7-2
C
3.某潜艇在海平面以下36米处上升(下潜)情况如下表(上升为正,下潜为负):
第1次 第2次 第3次 第4次 第5次
上升(下潜) +10米 -5米 -10米 +12米 -8米
第四次上升后,在( )
A.海平面以下29米 B.海平面以下31米
C 海平面以下41米 D.海平面以下26米
A
4.计算:
(1)0-(+8)+(-2.7)-(+1.3);
(2)-3.92+6.24-8.56+4.28;
解:(1)原式=-8+(-2.7)+(-1.3)
=-8+[(-2.7)+(-1.3)]
=-8+(-4)
=-12
(2)原式=-3.92-8.56+6.24+4.28
=-(3.92+8.56)+(6.24+4.28)
=-12.48+10.52
=-1.96
(3)
(4)
(3) (4)
(3)原式
(4)原式
有理数的加减混合运算
加减混合算式的读法与写法
有理数的加减混合运算
有理数的加减混合运算的应用
同课章节目录
