2.5 有理数的乘法与除法 课件(共56张PPT)2025-2026学年数学苏科版(2024)七年级上册
文档属性
| 名称 | 2.5 有理数的乘法与除法 课件(共56张PPT)2025-2026学年数学苏科版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:56:49 | ||
图片预览








文档简介
(共56张PPT)
第2章 有理数
2.5 有理数的乘法与除法
第2章 有理数
2.5 课时1 有理数的乘法
1.掌握有理数的乘法法则并能进行熟练地运算.
2.理解倒数的概念,会求一个有理数的倒数.
3.能应用有理数乘法解决简单的实际问题.
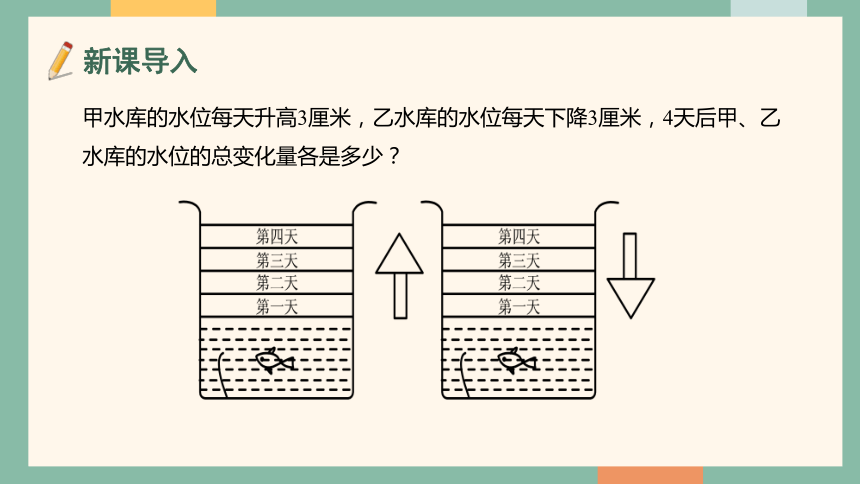
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库的水位的总变化量各是多少?
0
500
1000
1500
-500
-1000
-1500
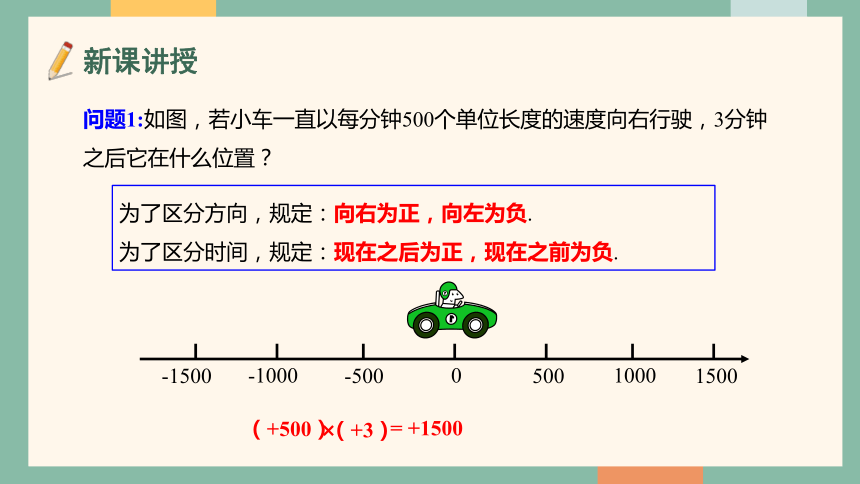
问题1:如图,若小车一直以每分钟500个单位长度的速度向右行驶,3分钟之后它在什么位置?
(+500)
×
(+3)
= +1500
为了区分方向,规定:向右为正,向左为负.
为了区分时间,规定:现在之后为正,现在之前为负.
0
500
1000
1500
-500
-1000
-1500
问题2:如图,若车一直以每分钟500个单位长度的速度向左行驶,3分钟之后它在什么位置?2分钟之后呢?1分钟之后呢?
(-500)
×
(+3)
= -1500
(-500)
×
(+2)
= -1000
(-500)
×
(+1)
= -500
问题3:若小车一直以每分钟500个单位长度的速度向右行驶到达原点,那么3分钟之前它在什么位置?2分钟之前呢?1分钟之前呢?
0
500
1000
1500
-500
-1000
-1500
(+500)
×
(-3)
= -1500
(+500)
×
(-2)
= -1000
(+500)
×
(-1)
= -500
通过问题2,3,我们得到下面几个式子:
(-500)×(+1) = -500
(- 500)×(+3) = -1500
(-500)×(+2) = -1000
(+500)×(-2) = -1000
(+500)×(-3) = -1500
(+500)×(-1) = -500
负数×正数
=负数
=负数
正数×负数
思考:根据上面的计算,你对一个负数乘一个正数有什么发现?
异号两数相乘,积为负,积的绝对值等于两个数的绝对值相乘.
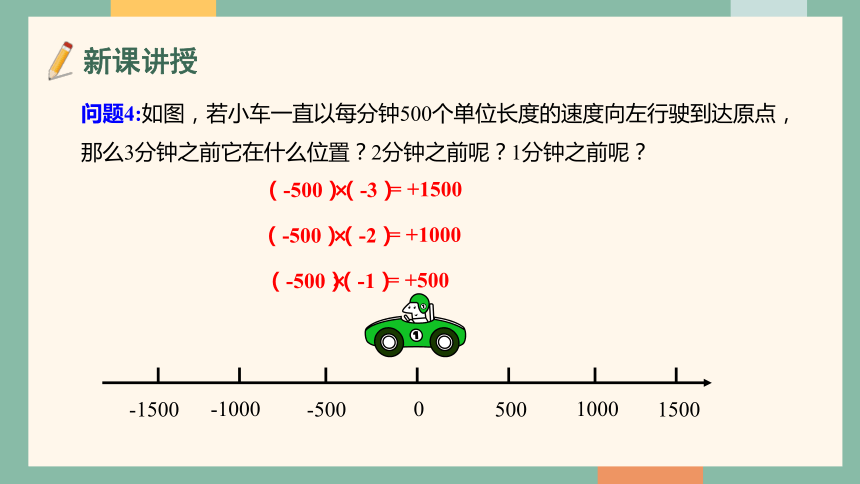
问题4:如图,若小车一直以每分钟500个单位长度的速度向左行驶到达原点,那么3分钟之前它在什么位置?2分钟之前呢?1分钟之前呢?
0
500
1000
1500
-500
-1000
-1500
(-500)
×
(-3)
= +1500
(-500)
×
(-2)
= +1000
(-500)
×
(-1)
= +500
通过问题4,我们得到3个式子:
(-500)×(-3)= +1500
(- 500)×(-2)= + 1000
(-500)×(- 1)= +500
思考 根据上面的计算,你对两个负数相乘有什么发现?
同号两数相乘,积为正,积的绝对值等于两个数的绝对值相乘
负数×负数
=正数
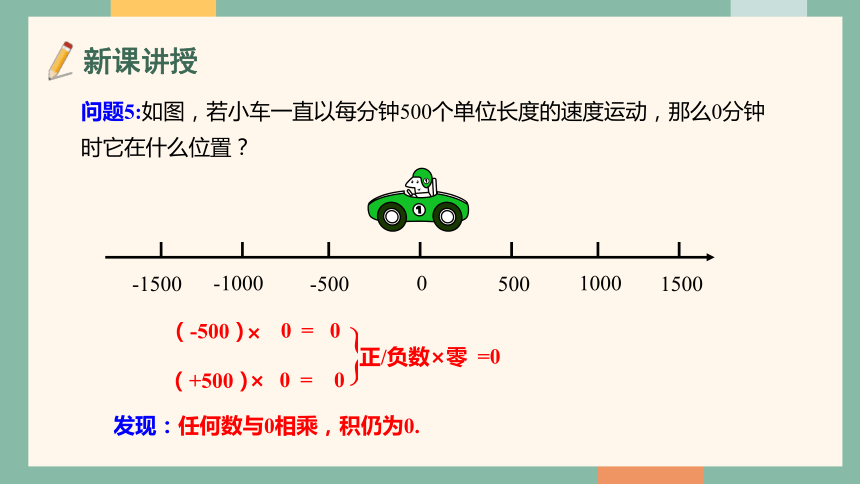
问题5:如图,若小车一直以每分钟500个单位长度的速度运动,那么0分钟时它在什么位置?
0
500
1000
1500
-500
-1000
-1500
(-500)
×
0
= 0
(+500)
×
0
= 0
正/负数×零
=0
发现:任何数与0相乘,积仍为0.
归纳总结
有理数乘法法则:
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数与0相乘,仍得0.
有理数乘法的符号法则
(1) 如果两个数的积为正数,那么这两个数同正或同负,反之亦然,即: ab>0 a>0, b>0 或 a<0, b<0.
(2) 如果两个数的积为负数,那么这两个数一正一负,反之亦然,即: ab<0 a>0, b<0 或 a<0, b>0.
(3) 如果两个数的积为 0,那么这两个数中至少有一个数是 0,反之亦然,即: ab=0 a=0 或 b=0.
快速抢答:确定下列两数积的符号并给出结果.
负号,=-10
负号,=-12
正号,=14
正号,=
(1) 5×(- 2)
(2)(- 3)×4
(3)(- 2)×(- 7)
(4)
例1 计算:
(1)(-3)×7;(2)0.1×(-100);(3)(-6)×(-);(4)(-)×(-).
解:(1)(-3)×7=-(3×7)=-21.
(2)0.1×(-100)=-(0.1×100)=-10.
(3)(-6)×(-)=+(6×)=1.
(4)(-)×(-)=+(×)=.
有理数乘法的求解步骤:
先确定积的符号;
再求绝对值的积.
(-6)×(-)=1这两个数有什么特点?
互为倒数
结论:
如果两个数的乘积是1,那么我们称这两个有理数互为倒数,其中一个数称为另一个数的倒数.
说一说:说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
-3,
归纳总结
(1)求一个数的倒数,不能改变它的性质符号,即一个正数的倒数是正数,一个负数的倒数是负数;
(2)求小数或带分数时的倒数时,先将小数或带分数化为分数或者假分数,再颠倒其分子和分母的位置.
例2 甲水库的水位每天升高3 cm,乙水库的水位每天下降5 cm,4天后,甲、乙水库水位总的变化量各是多少?
答:甲、乙水库水位总的变化量分别为甲水库水位上升12cm,乙水库水位下降20cm.
解:3×4=12(cm)
-5×4=-20(cm)
1.计算 ( - 1 ) × 3 的结果是( )
A. -3 B. - 2 C. 2 D. 3
2.下列计算正确的有( )
①(-3)×(-4)=-12; ②(-2)×5=-10;
③(-41)×(-1)=-41; ④24×(-5)=120.
A.1个 B.2个
C.3个 D.4个
A
A
3.下列各组数中互为倒数的是( )
A. 5与 - ( - 5) B. - (+5)与- | - |
C. +( - ) 与- | | D. +( - 5)与- (- )
4.在 2, 3, - 5, 7 这四个数中,任取两个数相乘,得到的积最小的是( )
A. 6 B. 35
C. - 21 D. - 35
B
D
第2章 有理数
2.5 课时2 有理数的乘法运算律
1.掌握有理数的乘法运算律,并利用运算律简化乘法运算;
2.掌握多个有理数相乘的符号法则.
乘法交换律:ab=ba,
乘法结合律:(ab)c=a(bc).
乘法对加法的分配律:a(b+c)=ab+ac.
你能叙述下小学学过的乘法运算律吗?
(1) (-2)×4=_______ , 4×(-2)=________.
(-5)×(-7)=_______ ,(-5)×(-7)=_______ .
问题1:在有理数的范围内,乘法的交换律和结合律是否仍然适用?
-8
-8
6
-24
12
-24
乘法交换律仍然成立
乘法结合律仍然成立
(2) [(-2)×(-3)]×(-4)=_____×(-4)=______ ,
(-2)×[(-3)×(-4)]=(-2)×_____=_______.
[(-15)×(-)]×(-10)=_____×(-10)=______ ,
(-15)×[(-)×(-10)]=(-15)×_____=_______.
35
35
3
-30
2
-30
例1:计算:
(1)(-0.25) ×(-)×(-4) ;(2)100× ×(-8) ×(-0.1).
解:(1)原式=(-0.25)×(-4)×(-)
=[(-0.25)×(-4) ]×(-)
=1×(-)
=-
(2)原式=100×(-0.1)× ×(-)
=[100×(-0.1)]×[×(-)]
=(-10)×(-)
=15
运用交换律
运用结合律
问题2:在有理数的范围内,乘法对加法的分配律是否仍然适用?
(1) (-6)×[4+(-9)]=(-6)×______=_______,
(-6)×4+(-6)×(-9)=____+____=_______;
(2) 5×[(-8)+(-3)]=5×_______=_________.
5×(-8)+5×(-3)=____+____=________.
-5
30
-24
54
30
-11
-55
-40
-15
-55
乘法对加法的分配律(简称分配律)
仍然成立
归纳总结
有理数乘法的运算律:
(1)乘法交换律:两个有理数相乘,交换两个因数的位置,积不变.ab=ba
(2)乘法结合律:三个有理数相乘,可以先把前面两个数相乘,
再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变. (ab)c=a(bc)
(3)乘法分配律:一个有理数同两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加. a(b+c)=ab+ac
例2:计算:- ×(10- - ) .
解:原式= (-)×10+ (-)× +(-)×( - )
=-6+1+
=-.
例3:用简便方法计算:(- 47.65)× 2 +37.15× 2 +10.5×(- 7 ).
解:原式 =[( - 47.65) +37.15] × 2 +10.5× (- 7 )
= (- 10.5) × 2 +10.5×( - 7
= (- 10.5) × (2 +7 )
= (- 10.5) × 10
= - 105.
快速说出结果:
(2)2×3×4×(-5)
(3)2×3×(-4) ×(-5)
(4) 2×(-3) ×(-4) ×(-5)
(5) (-2) ×(-3) ×(-4) ×(-5)
=-120
=+120
=-120
=+120
(1)2×3×4×(5)
=+120
通过上面的计算填写下表.
算式 (1) (2) (3) (4) (5)
负因数的个数
积的符号 ﹢ - ﹢ - ﹢
0
1
2
4
3
思考:观察上面填写的结果,积的符号与负因数的个数有什么关系
积的符号与负因数的个数之间的关系
(1)当负因数的个数是偶数时,积是正数;
几个不等于零的数相乘,积的符号由负因数的个数决定:
(2)当负因数的个数是奇数时,积是负数.
注意:多个有理数相乘,有一个因数为0时,积为0.
归纳总结
例3:计算:(1) (-6)×(-5)×3 (2)(-4)×(-3)×(-2 )
解:(1)原式=6×5×3
=90
(2)原式=-(4×3×2)
=-24
(3) -20×0.15×(-1.2)×(-3)
(3)原式=-(20×0.15×1.2×3)
=-10.8
(4)
(4)原式=
归纳总结
利用多个有理数相乘的法则,先确定符号,再计算绝对值的乘积 .
1.计算(-2)×(3-),用乘法分配律计算过程正确的是 ( )
A.(-2)×3+(-2)×(- )
B.(-2)×3-(-2)×(- )
C.2×3-(-2)×(- )
D.(-2)×3+2×(- )
A
2.有2024个有理数相乘,如果积为0,那么这2020个有理数( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
3.下列算式中,积为负数的是( )
A.(-2)×(-5) B. 2×(-3.5)×(-6.5)
C.(-1.5)×(-2)×(-3) D.(-1)×(- ) × 0
C
C
4.下列计算(-55)×99+(-44)×99-99正确的是( )
A.原式=99×(-55-44)=-9 801
B.原式=99×(-55-44+1)=-9 702
C.原式=99×(-55-44-1)=-9 900
D.原式=99×(-55-44-99)=-19 602
C
5.计算.
(1)-2×3×(-5); (2)-6×(-5)×(-7);
(3)0.1×(-0.001)×(-1); (4)(-15)×(-49)×0×(-12)×37.
解:(1)原式=2×3×5=30;
(2)原式=30×(-7)=-210;
(3)原式=-0.0001×(-1)=0.0001;
(4)原式=0.
有理数乘法的运算律
有理数乘法的运算律
多个有理数相乘的符号法则
乘法交换律: ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律: a(b+c)=ab+ac
几个不为0的数相乘,负因数的个数是偶数个时,积是正数;负因数的个数是奇数个时,积是负数.
几个数相乘,如果有一个因数为0,积就为0.
第2章 有理数
2.5 课时3 有理数的除法
1.理解并掌握有理数的除法法则;
2.能运用有理数的除法法则进行运算.
小学中你学过的除法运算法则是什么?
除法是已知两个因数的积与其中一个因数,求另一个因数的运算.除法是乘法的逆运算.
该法则对有理数也适用吗?
试着填空:
(1)8×9=72,72÷9=_______,72× = _______;
(2)2×(-3)=-6,(-6)÷2=_______,(-6)× =_______;
(3)(-4)×2=-8,(-8)÷(-4)=_______,(-8)×( )=_______.
8
8
-3
-3
2
2
观察下列算式你有什么发现?
(1)72÷9=8,72× =8;
(2)(-6)÷2=-3 ,(-6)× =8;
(3)(-8)÷(-4)=2,(-8)×( )=2.
72÷9= 72× ,
(-6)÷2=(-6)× ,
(-8)÷(-4)=(-8)×( ).
有理数的除法可以转化为乘法吗?怎样转化?
有理数的除法法则一
除以一个数(不等于0)等于乘这个数的倒数.
这个法则也可以表示成
a÷b=a·(b≠0)
观察下面各组算式的结果,回答问题:
(1)18 ÷ 2=9,(-18)÷(-2)= 9,
(2) 18÷(-2) =- 9 ,18÷(- 9) =-2 ,(-18) ÷9 =-2,
(3) 0 ÷ 2= 0 ,0 ÷ a=0 ( a≠0 ).
(1)同号两数相除,商的符号怎样确定,结果等于什么?
同号两数相除,商为正,商的绝对值等于两个数的绝对值相除.
(2)异号两数相除,商的符号怎样确定,结果等于什么?
异号两数相除,商为负,商的绝对值等于两个数的绝对值相除.
(3)0除以任何一个不等于0的数,结果等于什么?
0除以任何一个不等于0的数,结果等于0.
有理数的除法法则二
两数相除,同号得正,异号得负,并把绝对值相除;0除以任何不等于0的数都得0.
在进行两个有理数的除法运算时,既可以先确定商的符号,再将绝对值相除,也可以将除法转化为乘法来进行.
例1:计算.
(1)(-2)÷0.25
(3) 14÷(-2) (4)0÷(-8)
解:
(1)原式=(-2)×4
=-8
(2)原式=()×=
(3)原式=-(14÷2)
=-7
(4)原式=0
例2:计算.
(1)(-)÷(-6)÷(-);(2)( - - + ) ÷(- ).
a÷b÷c=(a÷b) ÷c
解:(1)原式=(-)×(-)×(-)
=-( × × )
=-
(2)原式=(--+)×(-24)
=(-)×(-24)-×(-24)
=12+20-9
=23
1.下列计算正确的是( )
D
2.下面结论中正确的有( )
①若一个负数比它的倒数大,则这个负数的范围在-1与0之间
②若两数和为正,商为负,则这两个数异号,且负数的绝对值较小
③0除以任何数都得0
④任何整数都大于它的倒数
A.1个 B.2个 C.3个 D.4个
B
3.下列运算中,错误的是( )
A.÷(-4)=4×(-4) B.-5÷(-)=-5×(-2)
C.7-(-3)=7+3 D.6-7=(+6)+(-7)
4.计算 100÷10÷,结果正确的是( )
A.1 B.-1 C.100 D.-100
A
D
5.计算:(1)(-18)÷9÷(-2)
解:(1)(-18)÷9÷(-2)
=(-2)÷(-2)= 1
第2章 有理数
2.5 有理数的乘法与除法
第2章 有理数
2.5 课时1 有理数的乘法
1.掌握有理数的乘法法则并能进行熟练地运算.
2.理解倒数的概念,会求一个有理数的倒数.
3.能应用有理数乘法解决简单的实际问题.
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库的水位的总变化量各是多少?
0
500
1000
1500
-500
-1000
-1500
问题1:如图,若小车一直以每分钟500个单位长度的速度向右行驶,3分钟之后它在什么位置?
(+500)
×
(+3)
= +1500
为了区分方向,规定:向右为正,向左为负.
为了区分时间,规定:现在之后为正,现在之前为负.
0
500
1000
1500
-500
-1000
-1500
问题2:如图,若车一直以每分钟500个单位长度的速度向左行驶,3分钟之后它在什么位置?2分钟之后呢?1分钟之后呢?
(-500)
×
(+3)
= -1500
(-500)
×
(+2)
= -1000
(-500)
×
(+1)
= -500
问题3:若小车一直以每分钟500个单位长度的速度向右行驶到达原点,那么3分钟之前它在什么位置?2分钟之前呢?1分钟之前呢?
0
500
1000
1500
-500
-1000
-1500
(+500)
×
(-3)
= -1500
(+500)
×
(-2)
= -1000
(+500)
×
(-1)
= -500
通过问题2,3,我们得到下面几个式子:
(-500)×(+1) = -500
(- 500)×(+3) = -1500
(-500)×(+2) = -1000
(+500)×(-2) = -1000
(+500)×(-3) = -1500
(+500)×(-1) = -500
负数×正数
=负数
=负数
正数×负数
思考:根据上面的计算,你对一个负数乘一个正数有什么发现?
异号两数相乘,积为负,积的绝对值等于两个数的绝对值相乘.
问题4:如图,若小车一直以每分钟500个单位长度的速度向左行驶到达原点,那么3分钟之前它在什么位置?2分钟之前呢?1分钟之前呢?
0
500
1000
1500
-500
-1000
-1500
(-500)
×
(-3)
= +1500
(-500)
×
(-2)
= +1000
(-500)
×
(-1)
= +500
通过问题4,我们得到3个式子:
(-500)×(-3)= +1500
(- 500)×(-2)= + 1000
(-500)×(- 1)= +500
思考 根据上面的计算,你对两个负数相乘有什么发现?
同号两数相乘,积为正,积的绝对值等于两个数的绝对值相乘
负数×负数
=正数
问题5:如图,若小车一直以每分钟500个单位长度的速度运动,那么0分钟时它在什么位置?
0
500
1000
1500
-500
-1000
-1500
(-500)
×
0
= 0
(+500)
×
0
= 0
正/负数×零
=0
发现:任何数与0相乘,积仍为0.
归纳总结
有理数乘法法则:
1.两数相乘,同号得正,异号得负,并把绝对值相乘.
2.任何数与0相乘,仍得0.
有理数乘法的符号法则
(1) 如果两个数的积为正数,那么这两个数同正或同负,反之亦然,即: ab>0 a>0, b>0 或 a<0, b<0.
(2) 如果两个数的积为负数,那么这两个数一正一负,反之亦然,即: ab<0 a>0, b<0 或 a<0, b>0.
(3) 如果两个数的积为 0,那么这两个数中至少有一个数是 0,反之亦然,即: ab=0 a=0 或 b=0.
快速抢答:确定下列两数积的符号并给出结果.
负号,=-10
负号,=-12
正号,=14
正号,=
(1) 5×(- 2)
(2)(- 3)×4
(3)(- 2)×(- 7)
(4)
例1 计算:
(1)(-3)×7;(2)0.1×(-100);(3)(-6)×(-);(4)(-)×(-).
解:(1)(-3)×7=-(3×7)=-21.
(2)0.1×(-100)=-(0.1×100)=-10.
(3)(-6)×(-)=+(6×)=1.
(4)(-)×(-)=+(×)=.
有理数乘法的求解步骤:
先确定积的符号;
再求绝对值的积.
(-6)×(-)=1这两个数有什么特点?
互为倒数
结论:
如果两个数的乘积是1,那么我们称这两个有理数互为倒数,其中一个数称为另一个数的倒数.
说一说:说出下列各数的倒数:
1,-1, ,- ,5,-5,0.75,-
1,
-1,
3,
-3,
归纳总结
(1)求一个数的倒数,不能改变它的性质符号,即一个正数的倒数是正数,一个负数的倒数是负数;
(2)求小数或带分数时的倒数时,先将小数或带分数化为分数或者假分数,再颠倒其分子和分母的位置.
例2 甲水库的水位每天升高3 cm,乙水库的水位每天下降5 cm,4天后,甲、乙水库水位总的变化量各是多少?
答:甲、乙水库水位总的变化量分别为甲水库水位上升12cm,乙水库水位下降20cm.
解:3×4=12(cm)
-5×4=-20(cm)
1.计算 ( - 1 ) × 3 的结果是( )
A. -3 B. - 2 C. 2 D. 3
2.下列计算正确的有( )
①(-3)×(-4)=-12; ②(-2)×5=-10;
③(-41)×(-1)=-41; ④24×(-5)=120.
A.1个 B.2个
C.3个 D.4个
A
A
3.下列各组数中互为倒数的是( )
A. 5与 - ( - 5) B. - (+5)与- | - |
C. +( - ) 与- | | D. +( - 5)与- (- )
4.在 2, 3, - 5, 7 这四个数中,任取两个数相乘,得到的积最小的是( )
A. 6 B. 35
C. - 21 D. - 35
B
D
第2章 有理数
2.5 课时2 有理数的乘法运算律
1.掌握有理数的乘法运算律,并利用运算律简化乘法运算;
2.掌握多个有理数相乘的符号法则.
乘法交换律:ab=ba,
乘法结合律:(ab)c=a(bc).
乘法对加法的分配律:a(b+c)=ab+ac.
你能叙述下小学学过的乘法运算律吗?
(1) (-2)×4=_______ , 4×(-2)=________.
(-5)×(-7)=_______ ,(-5)×(-7)=_______ .
问题1:在有理数的范围内,乘法的交换律和结合律是否仍然适用?
-8
-8
6
-24
12
-24
乘法交换律仍然成立
乘法结合律仍然成立
(2) [(-2)×(-3)]×(-4)=_____×(-4)=______ ,
(-2)×[(-3)×(-4)]=(-2)×_____=_______.
[(-15)×(-)]×(-10)=_____×(-10)=______ ,
(-15)×[(-)×(-10)]=(-15)×_____=_______.
35
35
3
-30
2
-30
例1:计算:
(1)(-0.25) ×(-)×(-4) ;(2)100× ×(-8) ×(-0.1).
解:(1)原式=(-0.25)×(-4)×(-)
=[(-0.25)×(-4) ]×(-)
=1×(-)
=-
(2)原式=100×(-0.1)× ×(-)
=[100×(-0.1)]×[×(-)]
=(-10)×(-)
=15
运用交换律
运用结合律
问题2:在有理数的范围内,乘法对加法的分配律是否仍然适用?
(1) (-6)×[4+(-9)]=(-6)×______=_______,
(-6)×4+(-6)×(-9)=____+____=_______;
(2) 5×[(-8)+(-3)]=5×_______=_________.
5×(-8)+5×(-3)=____+____=________.
-5
30
-24
54
30
-11
-55
-40
-15
-55
乘法对加法的分配律(简称分配律)
仍然成立
归纳总结
有理数乘法的运算律:
(1)乘法交换律:两个有理数相乘,交换两个因数的位置,积不变.ab=ba
(2)乘法结合律:三个有理数相乘,可以先把前面两个数相乘,
再把结果与第三个数相乘;或者先把后两个数相乘,再把第一个数与所得结果相乘,积不变. (ab)c=a(bc)
(3)乘法分配律:一个有理数同两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加. a(b+c)=ab+ac
例2:计算:- ×(10- - ) .
解:原式= (-)×10+ (-)× +(-)×( - )
=-6+1+
=-.
例3:用简便方法计算:(- 47.65)× 2 +37.15× 2 +10.5×(- 7 ).
解:原式 =[( - 47.65) +37.15] × 2 +10.5× (- 7 )
= (- 10.5) × 2 +10.5×( - 7
= (- 10.5) × (2 +7 )
= (- 10.5) × 10
= - 105.
快速说出结果:
(2)2×3×4×(-5)
(3)2×3×(-4) ×(-5)
(4) 2×(-3) ×(-4) ×(-5)
(5) (-2) ×(-3) ×(-4) ×(-5)
=-120
=+120
=-120
=+120
(1)2×3×4×(5)
=+120
通过上面的计算填写下表.
算式 (1) (2) (3) (4) (5)
负因数的个数
积的符号 ﹢ - ﹢ - ﹢
0
1
2
4
3
思考:观察上面填写的结果,积的符号与负因数的个数有什么关系
积的符号与负因数的个数之间的关系
(1)当负因数的个数是偶数时,积是正数;
几个不等于零的数相乘,积的符号由负因数的个数决定:
(2)当负因数的个数是奇数时,积是负数.
注意:多个有理数相乘,有一个因数为0时,积为0.
归纳总结
例3:计算:(1) (-6)×(-5)×3 (2)(-4)×(-3)×(-2 )
解:(1)原式=6×5×3
=90
(2)原式=-(4×3×2)
=-24
(3) -20×0.15×(-1.2)×(-3)
(3)原式=-(20×0.15×1.2×3)
=-10.8
(4)
(4)原式=
归纳总结
利用多个有理数相乘的法则,先确定符号,再计算绝对值的乘积 .
1.计算(-2)×(3-),用乘法分配律计算过程正确的是 ( )
A.(-2)×3+(-2)×(- )
B.(-2)×3-(-2)×(- )
C.2×3-(-2)×(- )
D.(-2)×3+2×(- )
A
2.有2024个有理数相乘,如果积为0,那么这2020个有理数( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
3.下列算式中,积为负数的是( )
A.(-2)×(-5) B. 2×(-3.5)×(-6.5)
C.(-1.5)×(-2)×(-3) D.(-1)×(- ) × 0
C
C
4.下列计算(-55)×99+(-44)×99-99正确的是( )
A.原式=99×(-55-44)=-9 801
B.原式=99×(-55-44+1)=-9 702
C.原式=99×(-55-44-1)=-9 900
D.原式=99×(-55-44-99)=-19 602
C
5.计算.
(1)-2×3×(-5); (2)-6×(-5)×(-7);
(3)0.1×(-0.001)×(-1); (4)(-15)×(-49)×0×(-12)×37.
解:(1)原式=2×3×5=30;
(2)原式=30×(-7)=-210;
(3)原式=-0.0001×(-1)=0.0001;
(4)原式=0.
有理数乘法的运算律
有理数乘法的运算律
多个有理数相乘的符号法则
乘法交换律: ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律: a(b+c)=ab+ac
几个不为0的数相乘,负因数的个数是偶数个时,积是正数;负因数的个数是奇数个时,积是负数.
几个数相乘,如果有一个因数为0,积就为0.
第2章 有理数
2.5 课时3 有理数的除法
1.理解并掌握有理数的除法法则;
2.能运用有理数的除法法则进行运算.
小学中你学过的除法运算法则是什么?
除法是已知两个因数的积与其中一个因数,求另一个因数的运算.除法是乘法的逆运算.
该法则对有理数也适用吗?
试着填空:
(1)8×9=72,72÷9=_______,72× = _______;
(2)2×(-3)=-6,(-6)÷2=_______,(-6)× =_______;
(3)(-4)×2=-8,(-8)÷(-4)=_______,(-8)×( )=_______.
8
8
-3
-3
2
2
观察下列算式你有什么发现?
(1)72÷9=8,72× =8;
(2)(-6)÷2=-3 ,(-6)× =8;
(3)(-8)÷(-4)=2,(-8)×( )=2.
72÷9= 72× ,
(-6)÷2=(-6)× ,
(-8)÷(-4)=(-8)×( ).
有理数的除法可以转化为乘法吗?怎样转化?
有理数的除法法则一
除以一个数(不等于0)等于乘这个数的倒数.
这个法则也可以表示成
a÷b=a·(b≠0)
观察下面各组算式的结果,回答问题:
(1)18 ÷ 2=9,(-18)÷(-2)= 9,
(2) 18÷(-2) =- 9 ,18÷(- 9) =-2 ,(-18) ÷9 =-2,
(3) 0 ÷ 2= 0 ,0 ÷ a=0 ( a≠0 ).
(1)同号两数相除,商的符号怎样确定,结果等于什么?
同号两数相除,商为正,商的绝对值等于两个数的绝对值相除.
(2)异号两数相除,商的符号怎样确定,结果等于什么?
异号两数相除,商为负,商的绝对值等于两个数的绝对值相除.
(3)0除以任何一个不等于0的数,结果等于什么?
0除以任何一个不等于0的数,结果等于0.
有理数的除法法则二
两数相除,同号得正,异号得负,并把绝对值相除;0除以任何不等于0的数都得0.
在进行两个有理数的除法运算时,既可以先确定商的符号,再将绝对值相除,也可以将除法转化为乘法来进行.
例1:计算.
(1)(-2)÷0.25
(3) 14÷(-2) (4)0÷(-8)
解:
(1)原式=(-2)×4
=-8
(2)原式=()×=
(3)原式=-(14÷2)
=-7
(4)原式=0
例2:计算.
(1)(-)÷(-6)÷(-);(2)( - - + ) ÷(- ).
a÷b÷c=(a÷b) ÷c
解:(1)原式=(-)×(-)×(-)
=-( × × )
=-
(2)原式=(--+)×(-24)
=(-)×(-24)-×(-24)
=12+20-9
=23
1.下列计算正确的是( )
D
2.下面结论中正确的有( )
①若一个负数比它的倒数大,则这个负数的范围在-1与0之间
②若两数和为正,商为负,则这两个数异号,且负数的绝对值较小
③0除以任何数都得0
④任何整数都大于它的倒数
A.1个 B.2个 C.3个 D.4个
B
3.下列运算中,错误的是( )
A.÷(-4)=4×(-4) B.-5÷(-)=-5×(-2)
C.7-(-3)=7+3 D.6-7=(+6)+(-7)
4.计算 100÷10÷,结果正确的是( )
A.1 B.-1 C.100 D.-100
A
D
5.计算:(1)(-18)÷9÷(-2)
解:(1)(-18)÷9÷(-2)
=(-2)÷(-2)= 1
同课章节目录
