广东省深圳市福田区华富中学2023-2024学年九年级上学期期中数学试卷 (含答案)
文档属性
| 名称 | 广东省深圳市福田区华富中学2023-2024学年九年级上学期期中数学试卷 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 512.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 10:55:16 | ||
图片预览




文档简介
广东省深圳市福田区华富中学2023-2024学年九年级
上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.下列几何体的三视图相同的是( )
A. B.
C. D.
3.下列命题中,真命题是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直且相等的四边形是正方形
4.如图,直线ABCDEF,若AC=3,CE=4,则的值是( )
A. B. C. D.
5.一元二次方程的根的情况是( ).
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
6.已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都可能正面朝上
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
7.如图,和是以点O为位似中心的位似图形.若,则与的周长比是( )
A. B. C. D.
8.如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
9.若关于的一元二次方程的一个根是1,则的值是( )
A. B.1 C.1或 D.或0
10.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=S△ABF.其中正确的结论有( )个
A.4 B.3 C.2 D.1
二、填空题
11.的解是 .
12.如果,那么= .
13.在一个不透明的盒子中有20个大小相同的乒乓球,这些乒乓球除颜色外都相同,将盒中的乒乓球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回盒中,不断重复这一过程,共摸了1000次球,发现有400次摸到黄色乒乓球,估计这个盒子中的黄色乒乓球的个数是 .
14.一位同学想利用树影测树高,已知在某一时刻直立于地面长的竹竿的影长为,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高,落在地面部分影长,则树高
15.如图,正方形的边长为6,点E是边上一点,以为对角线作正方形,连接,则面积的最大值为 .
三、解答题
16.解方程:
(1);
(2).
17.琳琳有4盒外包装完全相同的糖果,其中有2盒巧克力味的,1盒牛奶味的,1盒水果味的,她准备和好朋友分享糖果.
(1)若琳琳随机打开1盒糖果,恰巧是牛奶味的概率是______;
(2)若琳琳从这4盒中随机挑选两盒打开,请用列表或画树状图法打开的两盒都是巧克力味的概率.
18.如图:
(1)在图中作出关于轴的对称图形,并写出点的坐标(_____,____);
(2)若点与点关于轴对称,则_____、_____;
(3)求的面积.
19.如图所示的是一圆柱形笔筒在灯光下的投影,已知该笔筒底面圆的直径,笔筒的高,点在灯光下的投影为点,点在灯光下的投影为点,过点作于点,,点,,,在同一直线上.
(1)求的长;
(2)求点到的距离.
20.“户太八号”葡萄是西安市葡萄研究所通过奥林匹亚芽变选育而成,近年来被广泛种植,某葡萄种植基地2020年种植了64亩,到2022年的种植面积达到100亩.
(1)求该基地这两年“户太八号”种植面积的平均增长率;
(2)某超市调查发现,当“户太八号”的售价为8元/千克时,每周能售出400千克,售价每上涨1元,每周销售量减少20千克.已知该超市“户太八号”的进价为6元/千克,为了维护消费者利益,物价部门规定,该水果售价不能超过15元/千克.若使销售“户太八号”每周获利2240元,则售价应上涨多少元?
21.如图,已知四边形ABCD,AD∥BC,对角线AC、BD交于点O,DO=BO,过点C作CE⊥AC,交BD的延长线于点E,交AD的延长线于点F,且满足∠DCE=∠ACB.
(1)求证:四边形ABCD是矩形;
(2)求证:.
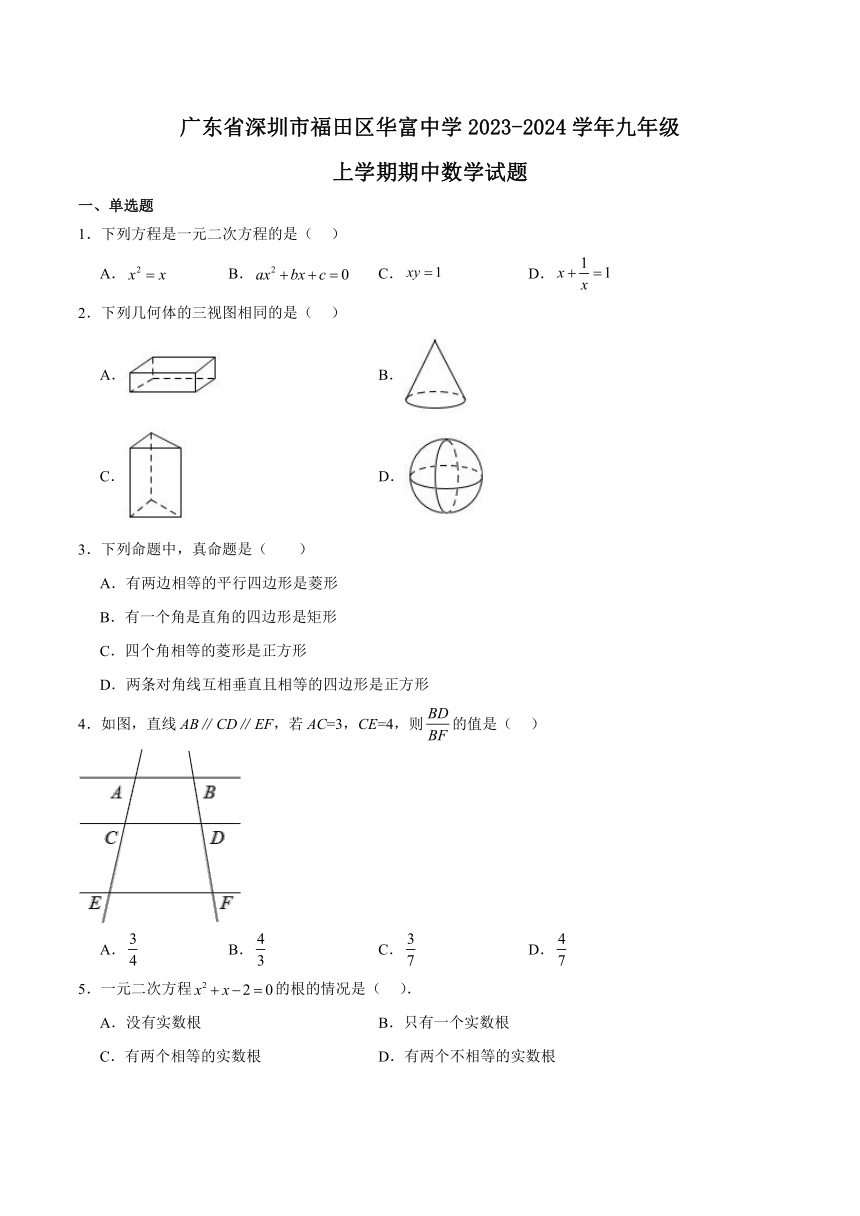
22.如图,在长方形中,的平分线交边于点,于点,连接并延长交边于点,连接交于点,若.
(1)求证:;
(2)求的度数;
(3)如果,求的值.
参考答案:
1.A
2.D
3.C
4.C
5.D
6.A
7.C
8.A
9.A
10.A
11...
12..
13.
14.4
15.
16.(1)解:∵,
∴,
∴,,,
∴,
∴,
∴,;
(2),
,
,
∴或,
解得:,.
17.(1);
故答案为:;
(2)用Q1 、Q2表示巧克力味的,N表示牛奶味的,S表示水果味的,列表如下:
糖果味道 Q1 Q2 N S
Q1 —————— Q1Q2 Q1N Q1S
Q2 Q2Q1 —————— Q2N Q2S
N NQ1 NQ2 —————— NS
S SQ1 SQ2 SN ——————
共12种等可能结果,其中两盒都是巧克力味的结果有2种,随机挑选两盒都是巧克力味的概率为:.
18.(1)解:如图,即为所作,
∴点的坐标为,
故答案为:;;
(2)∵点与点关于轴对称,
∴,
解得:,
故答案为:;;
(3),
∴的面积为.
19.(1)解:∵笔筒的高,即,,
∴,,
∴,
∴,
∴,
∵,,点,,,在同一直线上,
∴,
∴
经检验,是原方程的解且符合题意,
答:的长为;
(2)根据题意:,
∴,,
∴,
∴,
∵笔筒的高,,
∴,
解得:,
经检验,是原方程的解且符合题意,
∴.
答:点到的距离为.
20.(1)解:设该基地这两年“户太八号”种植面积的平均增长率为,
由题意得:,
解得或(不符合题意,舍去),
答:该基地这两年“户太八号”种植面积的平均增长率为.
(2)解:设售价应上涨元,则每周的销售量为千克,
由题意得:,
解得或,
∵为了维护消费者利益,物价部门规定,该水果售价不能超过15元/千克,
,
解得,
所以,
答:售价应上涨6元.
21.解:(1)证明∵AD∥BC,
∴,
∵DO=BO,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵CE⊥AC,
∴∠ACD+∠DCE=90°,
∵∠DCE=∠ACB,
∴∠ACB+∠ACD=90°,即∠BCD=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴AC=BD,∠ADC=90°,
∵AD∥BC,
∴,
∴,
∴,
∵∠ADC=∠ACF=90°,
∴,
∴.
22.(1)证明:∵四边形是长方形,
∴,
∵平分,
∴,
又∵,,
∴,,
∴、都是等腰直角三角形,
∴,,
∴,,
∵,
∴;
(2)解:∵,,,
∴,,
又∵,即,
∴,
∵,
∴,
∴的度数;
(3)∵,
∴,
∴,
∴,
由(2)得:,
∴,
∴,
∴,
∵四边形是长方形,,
∴,,
∴,
∴,
在,,
∴,
∴,
∴的值为.
上学期期中数学试题
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.下列几何体的三视图相同的是( )
A. B.
C. D.
3.下列命题中,真命题是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直且相等的四边形是正方形
4.如图,直线ABCDEF,若AC=3,CE=4,则的值是( )
A. B. C. D.
5.一元二次方程的根的情况是( ).
A.没有实数根 B.只有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
6.已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都可能正面朝上
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
7.如图,和是以点O为位似中心的位似图形.若,则与的周长比是( )
A. B. C. D.
8.如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
9.若关于的一元二次方程的一个根是1,则的值是( )
A. B.1 C.1或 D.或0
10.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=S△ABF.其中正确的结论有( )个
A.4 B.3 C.2 D.1
二、填空题
11.的解是 .
12.如果,那么= .
13.在一个不透明的盒子中有20个大小相同的乒乓球,这些乒乓球除颜色外都相同,将盒中的乒乓球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回盒中,不断重复这一过程,共摸了1000次球,发现有400次摸到黄色乒乓球,估计这个盒子中的黄色乒乓球的个数是 .
14.一位同学想利用树影测树高,已知在某一时刻直立于地面长的竹竿的影长为,但当他马上测量树影时,发现树的影子有一部分落在墙上.经测量,留在墙上的影高,落在地面部分影长,则树高
15.如图,正方形的边长为6,点E是边上一点,以为对角线作正方形,连接,则面积的最大值为 .
三、解答题
16.解方程:
(1);
(2).
17.琳琳有4盒外包装完全相同的糖果,其中有2盒巧克力味的,1盒牛奶味的,1盒水果味的,她准备和好朋友分享糖果.
(1)若琳琳随机打开1盒糖果,恰巧是牛奶味的概率是______;
(2)若琳琳从这4盒中随机挑选两盒打开,请用列表或画树状图法打开的两盒都是巧克力味的概率.
18.如图:
(1)在图中作出关于轴的对称图形,并写出点的坐标(_____,____);
(2)若点与点关于轴对称,则_____、_____;
(3)求的面积.
19.如图所示的是一圆柱形笔筒在灯光下的投影,已知该笔筒底面圆的直径,笔筒的高,点在灯光下的投影为点,点在灯光下的投影为点,过点作于点,,点,,,在同一直线上.
(1)求的长;
(2)求点到的距离.
20.“户太八号”葡萄是西安市葡萄研究所通过奥林匹亚芽变选育而成,近年来被广泛种植,某葡萄种植基地2020年种植了64亩,到2022年的种植面积达到100亩.
(1)求该基地这两年“户太八号”种植面积的平均增长率;
(2)某超市调查发现,当“户太八号”的售价为8元/千克时,每周能售出400千克,售价每上涨1元,每周销售量减少20千克.已知该超市“户太八号”的进价为6元/千克,为了维护消费者利益,物价部门规定,该水果售价不能超过15元/千克.若使销售“户太八号”每周获利2240元,则售价应上涨多少元?
21.如图,已知四边形ABCD,AD∥BC,对角线AC、BD交于点O,DO=BO,过点C作CE⊥AC,交BD的延长线于点E,交AD的延长线于点F,且满足∠DCE=∠ACB.
(1)求证:四边形ABCD是矩形;
(2)求证:.
22.如图,在长方形中,的平分线交边于点,于点,连接并延长交边于点,连接交于点,若.
(1)求证:;
(2)求的度数;
(3)如果,求的值.
参考答案:
1.A
2.D
3.C
4.C
5.D
6.A
7.C
8.A
9.A
10.A
11...
12..
13.
14.4
15.
16.(1)解:∵,
∴,
∴,,,
∴,
∴,
∴,;
(2),
,
,
∴或,
解得:,.
17.(1);
故答案为:;
(2)用Q1 、Q2表示巧克力味的,N表示牛奶味的,S表示水果味的,列表如下:
糖果味道 Q1 Q2 N S
Q1 —————— Q1Q2 Q1N Q1S
Q2 Q2Q1 —————— Q2N Q2S
N NQ1 NQ2 —————— NS
S SQ1 SQ2 SN ——————
共12种等可能结果,其中两盒都是巧克力味的结果有2种,随机挑选两盒都是巧克力味的概率为:.
18.(1)解:如图,即为所作,
∴点的坐标为,
故答案为:;;
(2)∵点与点关于轴对称,
∴,
解得:,
故答案为:;;
(3),
∴的面积为.
19.(1)解:∵笔筒的高,即,,
∴,,
∴,
∴,
∴,
∵,,点,,,在同一直线上,
∴,
∴
经检验,是原方程的解且符合题意,
答:的长为;
(2)根据题意:,
∴,,
∴,
∴,
∵笔筒的高,,
∴,
解得:,
经检验,是原方程的解且符合题意,
∴.
答:点到的距离为.
20.(1)解:设该基地这两年“户太八号”种植面积的平均增长率为,
由题意得:,
解得或(不符合题意,舍去),
答:该基地这两年“户太八号”种植面积的平均增长率为.
(2)解:设售价应上涨元,则每周的销售量为千克,
由题意得:,
解得或,
∵为了维护消费者利益,物价部门规定,该水果售价不能超过15元/千克,
,
解得,
所以,
答:售价应上涨6元.
21.解:(1)证明∵AD∥BC,
∴,
∵DO=BO,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵CE⊥AC,
∴∠ACD+∠DCE=90°,
∵∠DCE=∠ACB,
∴∠ACB+∠ACD=90°,即∠BCD=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴AC=BD,∠ADC=90°,
∵AD∥BC,
∴,
∴,
∴,
∵∠ADC=∠ACF=90°,
∴,
∴.
22.(1)证明:∵四边形是长方形,
∴,
∵平分,
∴,
又∵,,
∴,,
∴、都是等腰直角三角形,
∴,,
∴,,
∵,
∴;
(2)解:∵,,,
∴,,
又∵,即,
∴,
∵,
∴,
∴的度数;
(3)∵,
∴,
∴,
∴,
由(2)得:,
∴,
∴,
∴,
∵四边形是长方形,,
∴,,
∴,
∴,
在,,
∴,
∴,
∴的值为.
同课章节目录
