深圳市高级中学2024-2025学年八年级下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 深圳市高级中学2024-2025学年八年级下学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 738.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 10:43:18 | ||
图片预览



文档简介
广东省深圳市深圳高级中学2024-2025学年
八年级下学期数学期中试卷
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,如图四幅作品分别代表“立春”“立夏”“芒种”“大雪”,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.下列各式是分式的是( )
A. B. C. D.
3.下列各式中,从左到右的变形属于因式分解且正确的是( )
A. B.
C. D.
4.下列各式从左到右变形正确的是( )
A. B. C. D.
5.如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为( )
A. B. C.2.2 D.3
6.同一直角坐标系中,一次函数与正比例函数的图象如图所示,则满足的取值范围是( )
A. B. C. D.
7.若k为任意整数,则的值总能( )
A.被2整除 B.被3整除 C.被5整除 D.被7整除
8.已知关于x 的不等式组至少有2个整数解,则a 的取值范围是( )
A. B. C. D.
二、填空题
9.因式分解: .
10.当 时,分式的值为0.
11.若关于的方程的解为负数,则实数的取值范围是 .
12.两块不同的三角板按如图1所示摆放,AC与边重合,,.接着如图2保持三角板ACD不动,将三角板绕着点C按逆时针旋转后停止.在此旋转过程中,当与三角板ACD的一条边恰好平行时, .
13.如图所示的四边形中,,,, 则四边形的面积为 .
三、解答题
14.解不等式组:.
15.先化简,再求值:,其中.
16.某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
17.按要求完成作图:
(1)如图1,点A 、B 、C 、O都在格点上,绕点O 逆时针方向旋转得到,在图2中画出旋转后的.
(2)如图2,在内部求作一点P,使,并且点P 到两边的距离相等. (要求:用尺规作图,保留作图痕迹,不要求证明)
18.(1)证明:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于.
如图,在中,,,求证:
(2)如 图 , 是一张长方形纸片,且,沿 过 点D 的折痕将A 角翻折,使得点A 落在 上(如图中的点),折痕交 于 点G.那么 等于多少度?你能证明你的结论吗?(提示:可直接利用(1)的结论)
19.阅读与思考
配方法 把代数式通过配凑等手段,得到局部完全平方式(两数和的平方公式或两数差的平方公式),再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、最值问 题中都有着广泛的应用. 例如: ①用配方法因式分解: 原式 ②求的最小值. 解:先求出的最小值 ; 由于是非负数,所以,可得到,即的最小值为2. 进而的最小值为4.
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式: ;
(2)用配方法因式分解:;
(3)求 的最小值.
(4)已知实数x,y 满 足,求的最小值,并指出此时y的值.
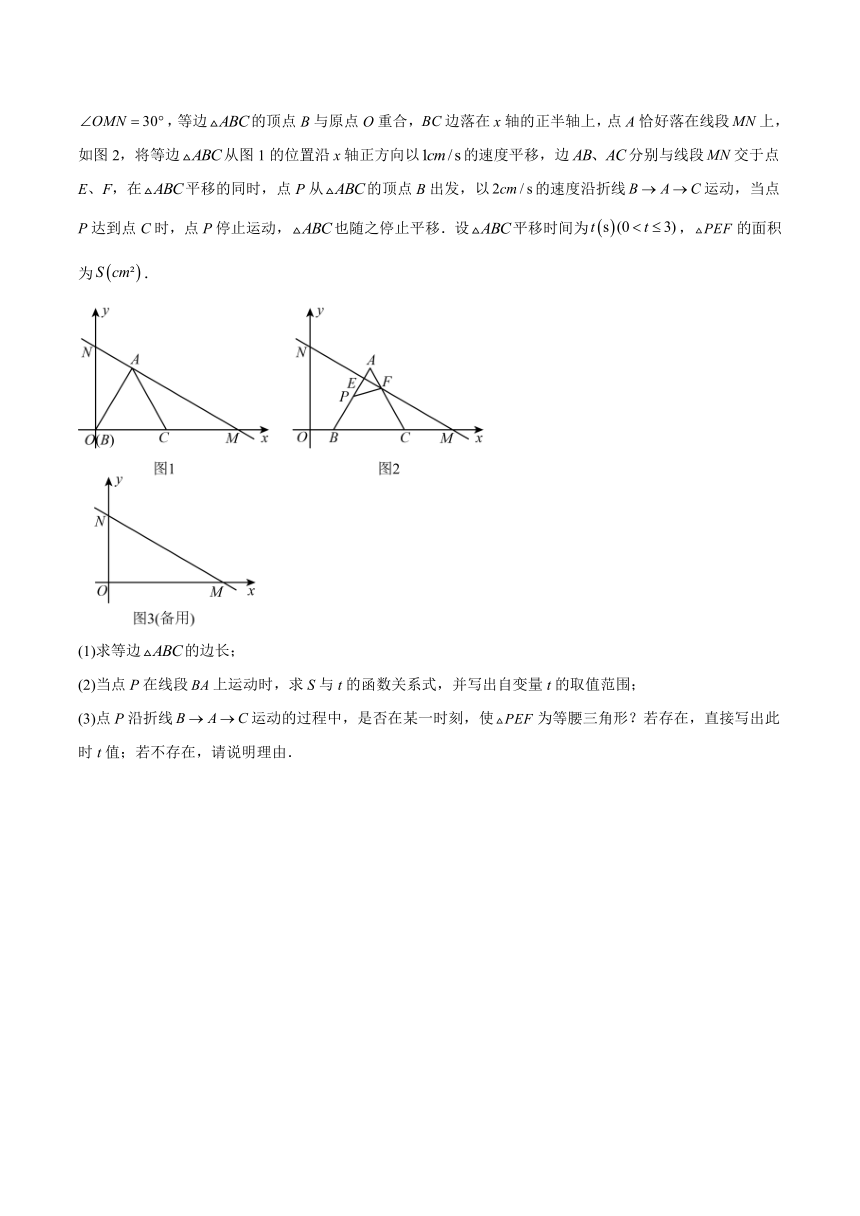
20.如图1,在平面直角坐标系中,直线分别与x轴正半轴、y轴正半轴交于点M、N,且,,等边的顶点B与原点O重合,边落在x轴的正半轴上,点A恰好落在线段上,如图2,将等边从图1的位置沿x轴正方向以的速度平移,边分别与线段交于点E、F,在平移的同时,点P从的顶点B出发,以的速度沿折线运动,当点P达到点C时,点P停止运动,也随之停止平移.设平移时间为,的面积为.
(1)求等边的边长;
(2)当点P在线段上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线运动的过程中,是否在某一时刻,使为等腰三角形?若存在,直接写出此时t值;若不存在,请说明理由.
参考答案
1.D
2.C
3.D
4.C
5.B
6.A
7.C
8.B
9.
10.
11./
12.或
13.
14.
15.
,
当时,原式.
16.(1);(2)公路运输方式运送的牛奶多,铁路运输方式所需用较少.
(1),
(2)
解得:,
解得:.
∵3000>2500,
∴公路运输方式运送的牛奶多,
∴(元),
(元).
∵1050>900,
∴铁路运输方式所需费用较少.
17.(1)如图1所示,即为所作:
(2)如图2所示,点P即为所作.
18.解:(1)证明:取中点,连接,
∵是直角三角形,,
,
∵,
,
∴是等边三角形,
,
.
(2)在长方形中,,
根据折叠可得,
∵,
,
∴,
,
,
,
.
19.(1)解:,
故答案为:4;
(2)解:
;
(3)解:
,
因为是非负数,
所以,
所以的最小值是 8 .
(4)解:∵,
∴,
代入得:
因为是非负数,
所以,
所以当时,取得最小值,最小值是 .
此时.
20.(1)
(2),
(3)存在,t值为或或2
(1)解:∵直线分别与轴正半轴,轴正半轴交于点,
,
∵为等边三角形,
,
∴,即为直角三角形,
.
(2)解:∵,
,
∵,
∴,
,
,即,
当点在上时,,
,
,
∴的面积,
即;
当点在上时,,
,
,
,
即;
(3)解:存在,有4种情况:
①当点在线段上时,
点在上运动的时间为,
∵为等腰三角形,,
∴,
∵,
∴,
∴或,
解得或(故舍去),
②当点在上时,
若时,点为的垂直平分线与的交点,此时为直角三角形斜边的中点,
∴,
∵点从的顶点出发,以的速度沿折线运动,
∴,
在直角三角形中,,
解得:,
若,,
则,
解得:;
③当在上时无解,
④当点在上时,,则,
所以,
解得,不合题意,舍去.
综上,存在值为或或2时,为等腰三角形.
八年级下学期数学期中试卷
一、单选题
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,如图四幅作品分别代表“立春”“立夏”“芒种”“大雪”,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.下列各式是分式的是( )
A. B. C. D.
3.下列各式中,从左到右的变形属于因式分解且正确的是( )
A. B.
C. D.
4.下列各式从左到右变形正确的是( )
A. B. C. D.
5.如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为( )
A. B. C.2.2 D.3
6.同一直角坐标系中,一次函数与正比例函数的图象如图所示,则满足的取值范围是( )
A. B. C. D.
7.若k为任意整数,则的值总能( )
A.被2整除 B.被3整除 C.被5整除 D.被7整除
8.已知关于x 的不等式组至少有2个整数解,则a 的取值范围是( )
A. B. C. D.
二、填空题
9.因式分解: .
10.当 时,分式的值为0.
11.若关于的方程的解为负数,则实数的取值范围是 .
12.两块不同的三角板按如图1所示摆放,AC与边重合,,.接着如图2保持三角板ACD不动,将三角板绕着点C按逆时针旋转后停止.在此旋转过程中,当与三角板ACD的一条边恰好平行时, .
13.如图所示的四边形中,,,, 则四边形的面积为 .
三、解答题
14.解不等式组:.
15.先化简,再求值:,其中.
16.某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
17.按要求完成作图:
(1)如图1,点A 、B 、C 、O都在格点上,绕点O 逆时针方向旋转得到,在图2中画出旋转后的.
(2)如图2,在内部求作一点P,使,并且点P 到两边的距离相等. (要求:用尺规作图,保留作图痕迹,不要求证明)
18.(1)证明:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于.
如图,在中,,,求证:
(2)如 图 , 是一张长方形纸片,且,沿 过 点D 的折痕将A 角翻折,使得点A 落在 上(如图中的点),折痕交 于 点G.那么 等于多少度?你能证明你的结论吗?(提示:可直接利用(1)的结论)
19.阅读与思考
配方法 把代数式通过配凑等手段,得到局部完全平方式(两数和的平方公式或两数差的平方公式),再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、最值问 题中都有着广泛的应用. 例如: ①用配方法因式分解: 原式 ②求的最小值. 解:先求出的最小值 ; 由于是非负数,所以,可得到,即的最小值为2. 进而的最小值为4.
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式: ;
(2)用配方法因式分解:;
(3)求 的最小值.
(4)已知实数x,y 满 足,求的最小值,并指出此时y的值.
20.如图1,在平面直角坐标系中,直线分别与x轴正半轴、y轴正半轴交于点M、N,且,,等边的顶点B与原点O重合,边落在x轴的正半轴上,点A恰好落在线段上,如图2,将等边从图1的位置沿x轴正方向以的速度平移,边分别与线段交于点E、F,在平移的同时,点P从的顶点B出发,以的速度沿折线运动,当点P达到点C时,点P停止运动,也随之停止平移.设平移时间为,的面积为.
(1)求等边的边长;
(2)当点P在线段上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线运动的过程中,是否在某一时刻,使为等腰三角形?若存在,直接写出此时t值;若不存在,请说明理由.
参考答案
1.D
2.C
3.D
4.C
5.B
6.A
7.C
8.B
9.
10.
11./
12.或
13.
14.
15.
,
当时,原式.
16.(1);(2)公路运输方式运送的牛奶多,铁路运输方式所需用较少.
(1),
(2)
解得:,
解得:.
∵3000>2500,
∴公路运输方式运送的牛奶多,
∴(元),
(元).
∵1050>900,
∴铁路运输方式所需费用较少.
17.(1)如图1所示,即为所作:
(2)如图2所示,点P即为所作.
18.解:(1)证明:取中点,连接,
∵是直角三角形,,
,
∵,
,
∴是等边三角形,
,
.
(2)在长方形中,,
根据折叠可得,
∵,
,
∴,
,
,
,
.
19.(1)解:,
故答案为:4;
(2)解:
;
(3)解:
,
因为是非负数,
所以,
所以的最小值是 8 .
(4)解:∵,
∴,
代入得:
因为是非负数,
所以,
所以当时,取得最小值,最小值是 .
此时.
20.(1)
(2),
(3)存在,t值为或或2
(1)解:∵直线分别与轴正半轴,轴正半轴交于点,
,
∵为等边三角形,
,
∴,即为直角三角形,
.
(2)解:∵,
,
∵,
∴,
,
,即,
当点在上时,,
,
,
∴的面积,
即;
当点在上时,,
,
,
,
即;
(3)解:存在,有4种情况:
①当点在线段上时,
点在上运动的时间为,
∵为等腰三角形,,
∴,
∵,
∴,
∴或,
解得或(故舍去),
②当点在上时,
若时,点为的垂直平分线与的交点,此时为直角三角形斜边的中点,
∴,
∵点从的顶点出发,以的速度沿折线运动,
∴,
在直角三角形中,,
解得:,
若,,
则,
解得:;
③当在上时无解,
④当点在上时,,则,
所以,
解得,不合题意,舍去.
综上,存在值为或或2时,为等腰三角形.
同课章节目录
