全册复习评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 全册复习评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 508.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 16:11:06 | ||
图片预览



文档简介
八年级上册全册复习 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.(2025天水武山县期中)在实数,,0.141 4,,,-,,-1,0.101 000 10…(相邻两个1之间依次增加2个0)中,其中是无理数的有 ( )
A.3个 B.4个 C.5个 D.6个
2.(2025重庆沙坪坝区期末)为了解七年级7 800名男生1 000 m长跑的国家体质测试情况,从中随机抽查了150名男生的1 000 m长跑成绩进行统计分析,下列说法正确的是 ( )
A.每名男生是个体
B.7 800名男生是总体
C.样本容量是150名
D.抽取的150名男生的1 000 m长跑的国家体质测试成绩是样本
3.下列运算正确的是 ( )
A.a3·a3=2a3 B.3a5÷a3=3a2
C.(a+b)2=a2+b2 D.(a+2)(a-2)=a2-2
4.用反证法证明“若实数a、b满足ab=0,则a、b中至少有一个是0”时,应先假设 ( )
A. a、b中至多有一个是0 B. a、b中至少有两个是0
C. a、b中没有一个是0 D. a、b都等于0
5.已知3m=5,9n=10,则3m+2n等于 ( )
A.25 B.50 C.200 D.500
6.若a=,b=|-6|,c=,则下列关系正确的为 ( )
A.a>b>c B.c>b>a C.b>a>c D.b>c>a
7.如图,AB⊥CD,且AB=CD,E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为 ( )
A.3 B.5 C.6 D.7
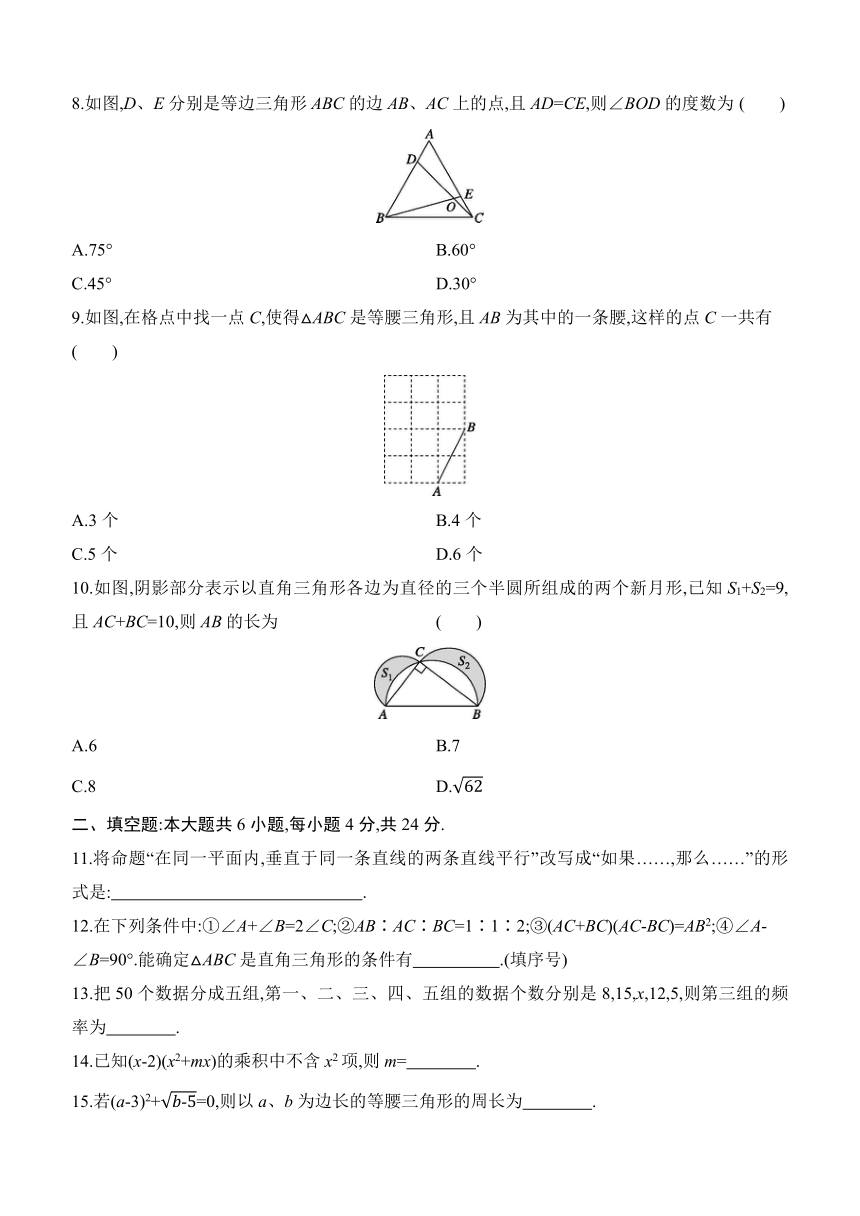
8.如图,D、E分别是等边三角形ABC的边AB、AC上的点,且AD=CE,则∠BOD的度数为 ( )
A.75° B.60°
C.45° D.30°
9.如图,在格点中找一点C,使得△ABC是等腰三角形,且AB为其中的一条腰,这样的点C一共有
( )
A.3个 B.4个
C.5个 D.6个
10.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=9,且AC+BC=10,则AB的长为 ( )
A.6 B.7
C.8 D.
二、填空题:本大题共6小题,每小题4分,共24分.
11.将命题“在同一平面内,垂直于同一条直线的两条直线平行”改写成“如果……,那么……”的形式是: .
12.在下列条件中:①∠A+∠B=2∠C;②AB∶AC∶BC=1∶1∶2;③(AC+BC)(AC-BC)=AB2;④∠A-
∠B=90°.能确定△ABC是直角三角形的条件有 .(填序号)
13.把50个数据分成五组,第一、二、三、四、五组的数据个数分别是8,15,x,12,5,则第三组的频率为 .
14.已知(x-2)(x2+mx)的乘积中不含x2项,则m= .
15.若(a-3)2+=0,则以a、b为边长的等腰三角形的周长为 .
16.某中学八年级甲、乙、丙三个班中,每班的学生人数都是40.某次数学考试的成绩统计如下:
丙班数学成绩频数分布表
分数段/分 50~60 60~70 70~80 80~90 90~100
人数(频数) 1 4 15 11 9
根据图表提供的信息(每组分数含最小值,不含最大值),则:
(1)甲班的数学成绩在80~90分这一组人数占全班人数的百分比为 ;
(2)三个班中,80~90分这一组人数最多的班是 班(填“甲”“乙”或“丙”).
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)(1)计算:-(-)2;
(2)分解因式:m2(a-2)+n2(2-a).
18.(6分)计算:
(1)(2x2y)3·5xy2÷(-10x2y4);
(2)(3x4-2x3)÷(-x)-(x-x2)·3x.
19.(6分)先化简,再求值:[(3y-x)(3y+x)-(2x+y)2-8y2]÷x,其中x2-4x+4+|y-3|=0.
20.(8分)已知2a-1的平方根是±3,b-9的立方根是2,c是的整数部分.
(1)求a、b、c的值;
(2)若x是的小数部分,求x(+3)的算术平方根.
21.(10分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点E是AB的中点,连结ED并延长,交BC的延长线于点F,连结AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
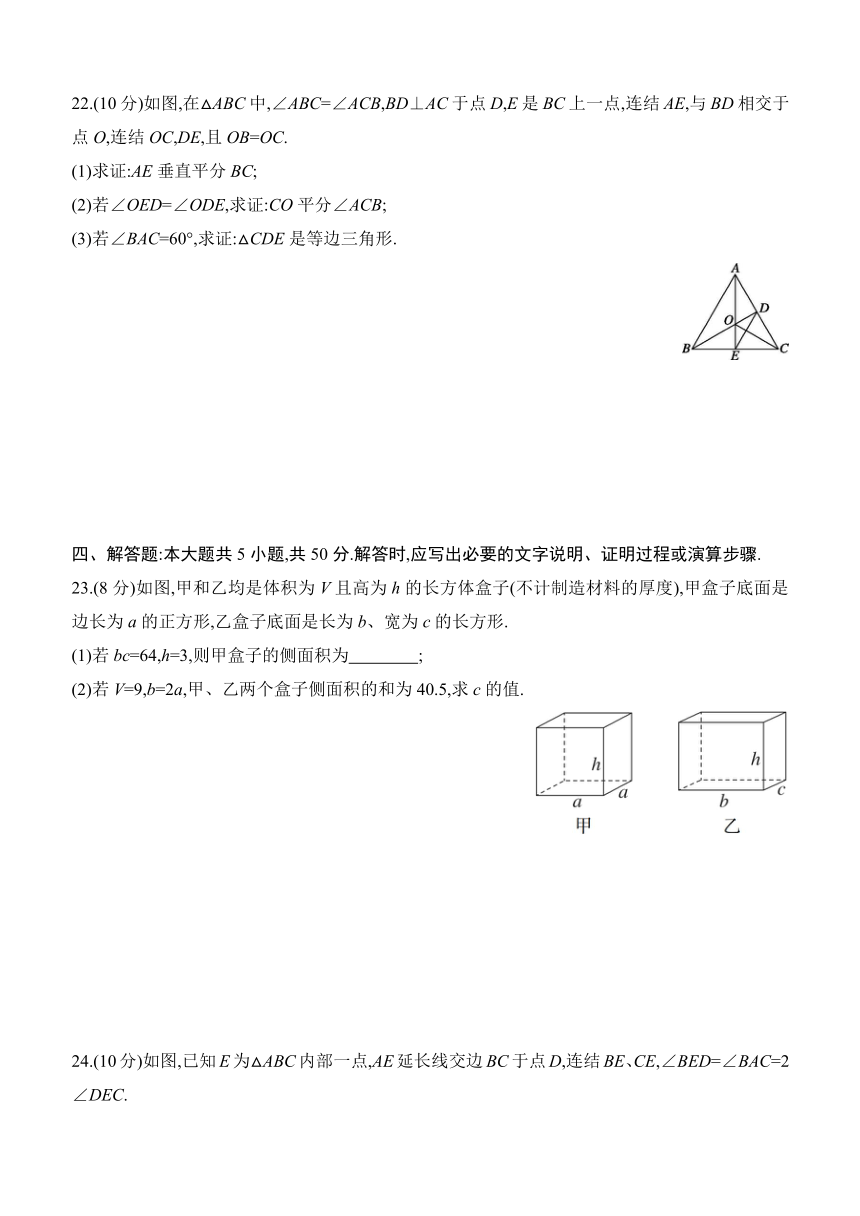
22.(10分)如图,在△ABC中,∠ABC=∠ACB,BD⊥AC于点D,E是BC上一点,连结AE,与BD相交于点O,连结OC,DE,且OB=OC.
(1)求证:AE垂直平分BC;
(2)若∠OED=∠ODE,求证:CO平分∠ACB;
(3)若∠BAC=60°,求证:△CDE是等边三角形.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,甲和乙均是体积为V且高为h的长方体盒子(不计制造材料的厚度),甲盒子底面是边长为a的正方形,乙盒子底面是长为b、宽为c的长方形.
(1)若bc=64,h=3,则甲盒子的侧面积为 ;
(2)若V=9,b=2a,甲、乙两个盒子侧面积的和为40.5,求c的值.
24.(10分)如图,已知E为△ABC内部一点,AE延长线交边BC于点D,连结BE、CE,∠BED=∠BAC=2∠DEC.
(1)求证:∠CAE=∠ABE;
(2)若AC=AB,求证:BE=2AE.
25.(10分)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A、B,道路AC因为施工需要封闭,该村为方便村民取水,决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条道路CH,已知CB= km,CH=3 km,HB=2 km.
(1)CH是否为村庄C到河边最近的道路 请通过计算加以说明.
(2)已知新的取水点H与原取水点A相距1 km,求新路CH比原路CA少多少千米.
26.(10分)某学校为了解学生对“航空航天知识”的掌握情况,从七年级随机抽取部分同学进行测试,并对成绩(百分制)进行整理、描述和分析,下面给出部分信息:
a.学生成绩的统计图如图(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100).
b.在80≤x<90这一组成绩的是80,80,80,81,81,82,83,84,84,85,85,87,88,89,89,89.
c.成绩不低于90分为优秀.
根据以上信息,解答下列问题:
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)70≤x<80这组有 名同学,80≤x<90这组学生人数所占的百分比为 ;
(3)补全频数分布直方图;
(4)把调查结果推广到全年级,若七年级有400名学生,请估计该校七年级学生达到优秀的人数.
27.(12分)(2024宁夏中考)综合与实践
如图1,在△ABC中,BD是∠ABC的平分线,BD的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB;
结论2:当图1中∠ACB=90°时,如图2所示,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与GE的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连结FH、AG,延长AG交FH于点N,补全图形,求证:FN=HN+AE.
【详解答案】
1.C
2.D 解析:在这个问题中,每一名男生的1 000 m长跑的国家体质测试的成绩是个体,七年级7 800名男生1 000 m长跑的国家体质测试成绩是总体,抽取150名男生的1 000 m长跑的国家体质测试成绩是总体的一个样本,150是样本容量.
故选D.
3.B 解析:A.a3·a3=a6,故原计算错误,不符合题意;B.3a5÷a3=3a2,计算正确,符合题意;C.(a+b)2=a2+2ab+b2,故原计算错误,不符合题意;D.(a+2)(a-2)=a2-4,故原计算错误,不符合题意.故选B.
4.C 解析:“若实数a、b满足ab=0,则a、b中至少有一个是0.”第一步应假设a、b中没有一个是0.故选C.
5.B 解析:当3m=5,9n=10时,
3m+2n=3m×32n
=3m×9n
=5×10
=50.
故选B.
6.C 解析:∵b=|-6|=6,c=,∴b=6,c<5,5∴b>a>c.
故选C.
7.B 解析:由题意得△ABF≌△CDE,
∴AF=CE=4,DE=BF=3.
∵EF=2,
∴AD=AF+DF=AF+DE-EF=4+3-2=5.
故选B.
8.B 解析:∵△ABC是等边三角形,
∴∠BCE=∠CAD=60°,BC=CA,
在△BCE和△CAD中,
∴△BCE≌△CAD(SAS),
∴∠CBE=∠ACD,
∴∠BOD=∠OCB+∠CBE=∠OCB+∠ACD=∠ACB=60°.
故选B.
9.C 解析:如图,点C的位置共有5个.
故选C.
10.C 解析:由勾股定理,得AC2+BC2=AB2,
∵S1+S2=9,
∴×π×π×AC×BC-π×=9.
∴AC×BC=18.
∵AC+BC=10.
∴AB===
=8.
故选C.
11.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
12.③ 解析:①∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴2∠C+∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴不能判定△ABC为直角三角形.故①不符合题意;
②∵AB∶AC∶BC=1∶1∶2,
∴AB+AC=BC.
∴构不成三角形.
∴△ABC不是直角三角形.故②不符合题意;
③∵(AC+BC)(AC-BC)=AB2,
∴AC2-BC2=AB2.
∴AB2+BC2=AC2.
∴△ABC是直角三角形.故③符合题意;
④∵∠A-∠B=90°,
∴不能判定△ABC为直角三角形.故④不符合题意.
13.0.2 解析:根据题意,得第三组数据的个数为x=50-(8+15+12+5)=10,
故第三组的频率为10÷50=0.2.
14.2 解析:(x-2)(x2+mx)
=x3+mx2-2x2-2mx
=x3+(m-2)x2-2mx,
∵乘积中不含x2项,
∴m-2=0.
解得m=2.
15.11或13 解析:∵(a-3)2+=0,(a-3)2≥0,≥0,∴a-3=0,b-5=0.∴a=3,b=5.当3为腰长时,所求等腰三角形的周长=3+5+3=11;当5为腰长时,所求等腰三角形的周长=3+5+5=13.
16. (1)40% (2)甲 解析:(1)40-2-5-12-5=16(人),
16÷40×100%=40%.
(2)100%-35%-10%-5%-20%=30%,
40×30%=12(人),
即乙班80~90分这一组人数为12.
又因为在80~90分这一组,甲班有16人,丙班有11人,
所以三个班中,80~90分这一组人数最多的班是甲班.
17.解:(1)原式=3-(-2)-5=0.
(2)原式=(a-2)(m2-n2)
=(a-2)(m+n)(m-n).
18.解:(1)原式=8x6y3·5xy2÷(-10x2y4)
=40x7y5÷(-10x2y4)
=-4x5y.
(2)原式=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2.
19.解:[(3y-x)(3y+x)-(2x+y)2-8y2]÷x
=(9y2-x2-4x2-4xy-y2-8y2)÷x
=(-5x2-4xy)÷x
=-10x-8y.
∵x2-4x+4+|y-3|=0,
∴(x-2)2+|y-3|=0.
∴x-2=0,y-3=0.
∴x=2,y=3.
当x=2,y=3时,
原式=-10×2-8×3
=-20-24
=-44.
20.解:(1)∵2a-1的平方根是±3,
∴2a-1=9.
∴a=5.
∵b-9的立方根是2,
∴b-9=8.
∴b=17.
∵c是的整数部分,而3<<4,
∴c=3.
∴a=5,b=17,c=3.
(2)∵3<<4,x是的小数部分,
∴x=-3.
∴x(+3)=(-3)×(+3)=3.
∴x(+3)的算术平方根为.
21.(1)解:设∠BAC=x°,
∵AD=BD,
∴∠BAC=∠ABD=x°.
∴∠BDC=2x°.
∵BD=BC,
∴∠BDC=∠BCD=2x°.
∵AB=AC,
∴∠ABC=∠ACB=2x°.
由∠BAC+∠ABC+∠ACB=180°可得x+2x+2x=180,
解得x=36,
∴∠BAC=36°,∠ACB=72°.
(2)证明:∵E是AB的中点,AD=BD,
∴DE⊥AB,即FE⊥AB.
∴AF=BF.
∴∠BAF=∠ABF.
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,
∴∠AFC=∠ACB-∠CAF=36°.
∴∠CAF=∠AFC=36°.
∴AC=CF,即△ACF是等腰三角形.
22.证明:(1)∵∠ABC=∠ACB,
∴AB=AC.
∵OB=OC,点A、O在AE上,
∴AE垂直平分BC.
(2)∵∠OED=∠ODE,
∴OD=OE.
又∵BD⊥AC,AE⊥BC,
即OD⊥AC,OE⊥BC,
∴CO平分∠ACB.
(3)由(1)知AB=AC.
∵∠BAC=60°,
∴△ABC是等边三角形.
∴AB=BC=AC,∠ABC=∠ACB=60°.
由(1)知AE垂直平分BC,
∴E是BC的中点.
∴EC=BC.
∵BD⊥AC,
∴CD=AC.
∴EC=CD.
∴△CDE是等边三角形.
23.解:(1)96
(2)∵a2=bc,b=2a,∴a2=2ac.
∴a=2c.∴b=2a=4c.又∵甲、乙两个盒子侧面积的和=4ah+2bh+2ch=40.5,
∴18ch=40.5.∴ch=.
又∵V=bch=9,∴b=4.
∴c=1.
24.证明:(1)∵∠BED=∠ABE+
∠BAE,∠BAC=∠CAE+∠BAE,
且∠BED=∠BAC,
∴∠CAE=∠ABE.
(2)如图,在BE上截取EF=AE,连结AF,
则∠FAE=∠AFE=∠BED,
设∠BED=2α,
∴∠BED=∠BAC=2∠DEC=2α.
∴∠FAE=∠AFE=∠DEC=α.
∴∠AFB=∠AEC=180°-α.
在△ABF和△CAE中,
∴△ABF≌△CAE(AAS).
∴BF=AE=EF.
∴BE=2AE.
25.解:(1)CH为村庄C到河边最近的道路.
∵CH=3 km,HB=2 km,CB= km,
∴CH2+HB2=CB2.
∴△BCH为直角三角形,∠BHC=90°.
∴CH⊥AB.
∴CH为村庄C到河边最近的道路.
(2)在Rt△ACH中,
∵AH=1 km,CH=3 km,
∴AC=(km).
∵AC-CH=(-3)km,
∴新路CH比原路CA少(-3)km.
26. 解:(1)抽样调查 50
(2)14 32%
(3)补全频数分布直方图如下:
(4)400×=104.
答:估计该校七年级学生达到优秀的人数为104.
27.【发现结论】解:结论1:
结论2:AE=GE
【应用结论】证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA.
在△EFG和△EHA中,
∴△EFG≌△EHA(AAS).
∴FG=HA,即AH=GF.
(2)补全图形如图所示,
∵△EFG≌△EHA,
∴EA=EG,EH=EF.
∴在Rt△AEG中,∠EAG=∠EGA=45°,AG=AE.
∵∠FEH=90°,
∴∠EFH=∠EHF=45°.
∴∠AFN=∠FAN=45°,∠NGH=
∠AGE=45°.
∴FN=AN,∠NGH=∠NHG=45°.
∴GN=HN.
又∵AN=GN+AG,
∴FN=HN+AE.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.(2025天水武山县期中)在实数,,0.141 4,,,-,,-1,0.101 000 10…(相邻两个1之间依次增加2个0)中,其中是无理数的有 ( )
A.3个 B.4个 C.5个 D.6个
2.(2025重庆沙坪坝区期末)为了解七年级7 800名男生1 000 m长跑的国家体质测试情况,从中随机抽查了150名男生的1 000 m长跑成绩进行统计分析,下列说法正确的是 ( )
A.每名男生是个体
B.7 800名男生是总体
C.样本容量是150名
D.抽取的150名男生的1 000 m长跑的国家体质测试成绩是样本
3.下列运算正确的是 ( )
A.a3·a3=2a3 B.3a5÷a3=3a2
C.(a+b)2=a2+b2 D.(a+2)(a-2)=a2-2
4.用反证法证明“若实数a、b满足ab=0,则a、b中至少有一个是0”时,应先假设 ( )
A. a、b中至多有一个是0 B. a、b中至少有两个是0
C. a、b中没有一个是0 D. a、b都等于0
5.已知3m=5,9n=10,则3m+2n等于 ( )
A.25 B.50 C.200 D.500
6.若a=,b=|-6|,c=,则下列关系正确的为 ( )
A.a>b>c B.c>b>a C.b>a>c D.b>c>a
7.如图,AB⊥CD,且AB=CD,E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为 ( )
A.3 B.5 C.6 D.7
8.如图,D、E分别是等边三角形ABC的边AB、AC上的点,且AD=CE,则∠BOD的度数为 ( )
A.75° B.60°
C.45° D.30°
9.如图,在格点中找一点C,使得△ABC是等腰三角形,且AB为其中的一条腰,这样的点C一共有
( )
A.3个 B.4个
C.5个 D.6个
10.如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=9,且AC+BC=10,则AB的长为 ( )
A.6 B.7
C.8 D.
二、填空题:本大题共6小题,每小题4分,共24分.
11.将命题“在同一平面内,垂直于同一条直线的两条直线平行”改写成“如果……,那么……”的形式是: .
12.在下列条件中:①∠A+∠B=2∠C;②AB∶AC∶BC=1∶1∶2;③(AC+BC)(AC-BC)=AB2;④∠A-
∠B=90°.能确定△ABC是直角三角形的条件有 .(填序号)
13.把50个数据分成五组,第一、二、三、四、五组的数据个数分别是8,15,x,12,5,则第三组的频率为 .
14.已知(x-2)(x2+mx)的乘积中不含x2项,则m= .
15.若(a-3)2+=0,则以a、b为边长的等腰三角形的周长为 .
16.某中学八年级甲、乙、丙三个班中,每班的学生人数都是40.某次数学考试的成绩统计如下:
丙班数学成绩频数分布表
分数段/分 50~60 60~70 70~80 80~90 90~100
人数(频数) 1 4 15 11 9
根据图表提供的信息(每组分数含最小值,不含最大值),则:
(1)甲班的数学成绩在80~90分这一组人数占全班人数的百分比为 ;
(2)三个班中,80~90分这一组人数最多的班是 班(填“甲”“乙”或“丙”).
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)(1)计算:-(-)2;
(2)分解因式:m2(a-2)+n2(2-a).
18.(6分)计算:
(1)(2x2y)3·5xy2÷(-10x2y4);
(2)(3x4-2x3)÷(-x)-(x-x2)·3x.
19.(6分)先化简,再求值:[(3y-x)(3y+x)-(2x+y)2-8y2]÷x,其中x2-4x+4+|y-3|=0.
20.(8分)已知2a-1的平方根是±3,b-9的立方根是2,c是的整数部分.
(1)求a、b、c的值;
(2)若x是的小数部分,求x(+3)的算术平方根.
21.(10分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点E是AB的中点,连结ED并延长,交BC的延长线于点F,连结AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
22.(10分)如图,在△ABC中,∠ABC=∠ACB,BD⊥AC于点D,E是BC上一点,连结AE,与BD相交于点O,连结OC,DE,且OB=OC.
(1)求证:AE垂直平分BC;
(2)若∠OED=∠ODE,求证:CO平分∠ACB;
(3)若∠BAC=60°,求证:△CDE是等边三角形.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,甲和乙均是体积为V且高为h的长方体盒子(不计制造材料的厚度),甲盒子底面是边长为a的正方形,乙盒子底面是长为b、宽为c的长方形.
(1)若bc=64,h=3,则甲盒子的侧面积为 ;
(2)若V=9,b=2a,甲、乙两个盒子侧面积的和为40.5,求c的值.
24.(10分)如图,已知E为△ABC内部一点,AE延长线交边BC于点D,连结BE、CE,∠BED=∠BAC=2∠DEC.
(1)求证:∠CAE=∠ABE;
(2)若AC=AB,求证:BE=2AE.
25.(10分)如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A、B,道路AC因为施工需要封闭,该村为方便村民取水,决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条道路CH,已知CB= km,CH=3 km,HB=2 km.
(1)CH是否为村庄C到河边最近的道路 请通过计算加以说明.
(2)已知新的取水点H与原取水点A相距1 km,求新路CH比原路CA少多少千米.
26.(10分)某学校为了解学生对“航空航天知识”的掌握情况,从七年级随机抽取部分同学进行测试,并对成绩(百分制)进行整理、描述和分析,下面给出部分信息:
a.学生成绩的统计图如图(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100).
b.在80≤x<90这一组成绩的是80,80,80,81,81,82,83,84,84,85,85,87,88,89,89,89.
c.成绩不低于90分为优秀.
根据以上信息,解答下列问题:
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)70≤x<80这组有 名同学,80≤x<90这组学生人数所占的百分比为 ;
(3)补全频数分布直方图;
(4)把调查结果推广到全年级,若七年级有400名学生,请估计该校七年级学生达到优秀的人数.
27.(12分)(2024宁夏中考)综合与实践
如图1,在△ABC中,BD是∠ABC的平分线,BD的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB;
结论2:当图1中∠ACB=90°时,如图2所示,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与GE的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连结FH、AG,延长AG交FH于点N,补全图形,求证:FN=HN+AE.
【详解答案】
1.C
2.D 解析:在这个问题中,每一名男生的1 000 m长跑的国家体质测试的成绩是个体,七年级7 800名男生1 000 m长跑的国家体质测试成绩是总体,抽取150名男生的1 000 m长跑的国家体质测试成绩是总体的一个样本,150是样本容量.
故选D.
3.B 解析:A.a3·a3=a6,故原计算错误,不符合题意;B.3a5÷a3=3a2,计算正确,符合题意;C.(a+b)2=a2+2ab+b2,故原计算错误,不符合题意;D.(a+2)(a-2)=a2-4,故原计算错误,不符合题意.故选B.
4.C 解析:“若实数a、b满足ab=0,则a、b中至少有一个是0.”第一步应假设a、b中没有一个是0.故选C.
5.B 解析:当3m=5,9n=10时,
3m+2n=3m×32n
=3m×9n
=5×10
=50.
故选B.
6.C 解析:∵b=|-6|=6,c=,
故选C.
7.B 解析:由题意得△ABF≌△CDE,
∴AF=CE=4,DE=BF=3.
∵EF=2,
∴AD=AF+DF=AF+DE-EF=4+3-2=5.
故选B.
8.B 解析:∵△ABC是等边三角形,
∴∠BCE=∠CAD=60°,BC=CA,
在△BCE和△CAD中,
∴△BCE≌△CAD(SAS),
∴∠CBE=∠ACD,
∴∠BOD=∠OCB+∠CBE=∠OCB+∠ACD=∠ACB=60°.
故选B.
9.C 解析:如图,点C的位置共有5个.
故选C.
10.C 解析:由勾股定理,得AC2+BC2=AB2,
∵S1+S2=9,
∴×π×π×AC×BC-π×=9.
∴AC×BC=18.
∵AC+BC=10.
∴AB===
=8.
故选C.
11.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
12.③ 解析:①∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴2∠C+∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴不能判定△ABC为直角三角形.故①不符合题意;
②∵AB∶AC∶BC=1∶1∶2,
∴AB+AC=BC.
∴构不成三角形.
∴△ABC不是直角三角形.故②不符合题意;
③∵(AC+BC)(AC-BC)=AB2,
∴AC2-BC2=AB2.
∴AB2+BC2=AC2.
∴△ABC是直角三角形.故③符合题意;
④∵∠A-∠B=90°,
∴不能判定△ABC为直角三角形.故④不符合题意.
13.0.2 解析:根据题意,得第三组数据的个数为x=50-(8+15+12+5)=10,
故第三组的频率为10÷50=0.2.
14.2 解析:(x-2)(x2+mx)
=x3+mx2-2x2-2mx
=x3+(m-2)x2-2mx,
∵乘积中不含x2项,
∴m-2=0.
解得m=2.
15.11或13 解析:∵(a-3)2+=0,(a-3)2≥0,≥0,∴a-3=0,b-5=0.∴a=3,b=5.当3为腰长时,所求等腰三角形的周长=3+5+3=11;当5为腰长时,所求等腰三角形的周长=3+5+5=13.
16. (1)40% (2)甲 解析:(1)40-2-5-12-5=16(人),
16÷40×100%=40%.
(2)100%-35%-10%-5%-20%=30%,
40×30%=12(人),
即乙班80~90分这一组人数为12.
又因为在80~90分这一组,甲班有16人,丙班有11人,
所以三个班中,80~90分这一组人数最多的班是甲班.
17.解:(1)原式=3-(-2)-5=0.
(2)原式=(a-2)(m2-n2)
=(a-2)(m+n)(m-n).
18.解:(1)原式=8x6y3·5xy2÷(-10x2y4)
=40x7y5÷(-10x2y4)
=-4x5y.
(2)原式=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2.
19.解:[(3y-x)(3y+x)-(2x+y)2-8y2]÷x
=(9y2-x2-4x2-4xy-y2-8y2)÷x
=(-5x2-4xy)÷x
=-10x-8y.
∵x2-4x+4+|y-3|=0,
∴(x-2)2+|y-3|=0.
∴x-2=0,y-3=0.
∴x=2,y=3.
当x=2,y=3时,
原式=-10×2-8×3
=-20-24
=-44.
20.解:(1)∵2a-1的平方根是±3,
∴2a-1=9.
∴a=5.
∵b-9的立方根是2,
∴b-9=8.
∴b=17.
∵c是的整数部分,而3<<4,
∴c=3.
∴a=5,b=17,c=3.
(2)∵3<<4,x是的小数部分,
∴x=-3.
∴x(+3)=(-3)×(+3)=3.
∴x(+3)的算术平方根为.
21.(1)解:设∠BAC=x°,
∵AD=BD,
∴∠BAC=∠ABD=x°.
∴∠BDC=2x°.
∵BD=BC,
∴∠BDC=∠BCD=2x°.
∵AB=AC,
∴∠ABC=∠ACB=2x°.
由∠BAC+∠ABC+∠ACB=180°可得x+2x+2x=180,
解得x=36,
∴∠BAC=36°,∠ACB=72°.
(2)证明:∵E是AB的中点,AD=BD,
∴DE⊥AB,即FE⊥AB.
∴AF=BF.
∴∠BAF=∠ABF.
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,
∴∠AFC=∠ACB-∠CAF=36°.
∴∠CAF=∠AFC=36°.
∴AC=CF,即△ACF是等腰三角形.
22.证明:(1)∵∠ABC=∠ACB,
∴AB=AC.
∵OB=OC,点A、O在AE上,
∴AE垂直平分BC.
(2)∵∠OED=∠ODE,
∴OD=OE.
又∵BD⊥AC,AE⊥BC,
即OD⊥AC,OE⊥BC,
∴CO平分∠ACB.
(3)由(1)知AB=AC.
∵∠BAC=60°,
∴△ABC是等边三角形.
∴AB=BC=AC,∠ABC=∠ACB=60°.
由(1)知AE垂直平分BC,
∴E是BC的中点.
∴EC=BC.
∵BD⊥AC,
∴CD=AC.
∴EC=CD.
∴△CDE是等边三角形.
23.解:(1)96
(2)∵a2=bc,b=2a,∴a2=2ac.
∴a=2c.∴b=2a=4c.又∵甲、乙两个盒子侧面积的和=4ah+2bh+2ch=40.5,
∴18ch=40.5.∴ch=.
又∵V=bch=9,∴b=4.
∴c=1.
24.证明:(1)∵∠BED=∠ABE+
∠BAE,∠BAC=∠CAE+∠BAE,
且∠BED=∠BAC,
∴∠CAE=∠ABE.
(2)如图,在BE上截取EF=AE,连结AF,
则∠FAE=∠AFE=∠BED,
设∠BED=2α,
∴∠BED=∠BAC=2∠DEC=2α.
∴∠FAE=∠AFE=∠DEC=α.
∴∠AFB=∠AEC=180°-α.
在△ABF和△CAE中,
∴△ABF≌△CAE(AAS).
∴BF=AE=EF.
∴BE=2AE.
25.解:(1)CH为村庄C到河边最近的道路.
∵CH=3 km,HB=2 km,CB= km,
∴CH2+HB2=CB2.
∴△BCH为直角三角形,∠BHC=90°.
∴CH⊥AB.
∴CH为村庄C到河边最近的道路.
(2)在Rt△ACH中,
∵AH=1 km,CH=3 km,
∴AC=(km).
∵AC-CH=(-3)km,
∴新路CH比原路CA少(-3)km.
26. 解:(1)抽样调查 50
(2)14 32%
(3)补全频数分布直方图如下:
(4)400×=104.
答:估计该校七年级学生达到优秀的人数为104.
27.【发现结论】解:结论1:
结论2:AE=GE
【应用结论】证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA.
在△EFG和△EHA中,
∴△EFG≌△EHA(AAS).
∴FG=HA,即AH=GF.
(2)补全图形如图所示,
∵△EFG≌△EHA,
∴EA=EG,EH=EF.
∴在Rt△AEG中,∠EAG=∠EGA=45°,AG=AE.
∵∠FEH=90°,
∴∠EFH=∠EHF=45°.
∴∠AFN=∠FAN=45°,∠NGH=
∠AGE=45°.
∴FN=AN,∠NGH=∠NHG=45°.
∴GN=HN.
又∵AN=GN+AG,
∴FN=HN+AE.
