第11章 整式的乘除 评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 第11章 整式的乘除 评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览




文档简介
第11章 整式的乘除 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.计算(2m2)3的结果为 ( )
A.8m6 B.6m2 C.2m2 D.4m2
2.(2024徐州中考)下列运算正确的是 ( )
A.x3+x3=x6 B.x3·x9=x27
C.(x2)3=x5 D.x3÷x=x2
3.计算6x3÷3x2的结果是 ( )
A.x B.2x C.2x5 D.2x6
4.在进行多项式的乘法运算时,下列式子不能用平方差公式运算的是 ( )
A.(a+2b)(a-2b) B.(a+2b)(-a-2b)
C.(2a+b)(-2a+b) D.(2a-b)(-2a-b)
5.下列等式从左到右变形,是因式分解的是 ( )
A.2a-1=a(2-) B.x2-2x+1=(x-1)2
C.(a-b)(a+b)=a2-b2 D.x2+x+1=x(x+1)+1
6.(-×(-)2 026的计算结果是 ( )
A. B.- C. D.-
7.若用简便方法计算1 9992,应当用下列哪个式子 ( )
A.(2 000-1)2 B.(2 000-1)(2 000+1)
C.(1 999+1)(1 999-1) D.(1 999+1)2
8.下列各式从左到右的变形,正确的是 ( )
A.(x+y)2=-(x+y)2 B.(x-y)2=(-x-y)2
C.(x-y)2=(y-x)2 D.-(x-y)2=(y-x)2
9.如图,长方形的长和宽分别是x、y,它的周长为14,面积为10,则x2y+xy2的值为 ( )
A.140 B.70 C.14 D.10
10.如图,现有三种不同尺寸的卡片,分别是正方形卡片A、正方形卡片B和长方形卡片C.若要拼成一个长为a+2b、宽为2a+b的大长方形,则需要卡片C的张数为 ( )
A.3 B.4 C.5 D.6
二、填空题:本大题共6小题,每小题4分,共24分.
11.多项式8a3b2+6ab3c的公因式是 .
12.计算:3a2·(-7ab)= .
13.(2024常州中考)分解因式:x2-4xy+4y2= .
14.已知a2-b2=12,且a-b=-2,则a+b= .
15.若x2+x-2=0,则x3+2x2-x+2 025的值是 .
16.若x2+y2=10,xy=3,则代数式x-y的值为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
(1)(a3x4-0.9ax3)÷ax3;
(2)x(x-2y)+(x+y)2.
18.(6分)分解因式:(x+1)(x+2)+.
19.(6分)用简便方法计算:
(1)51×49;
(2)1052.
20.(8分)先化简,再求值:[(-y)·(-4y)+(x-2y)2-(3y)2]·2y,其中x=-3,y=.
21.(10分)已知A=x,B是多项式,在计算B+A时,小明把B+A看成B÷A,计算结果是x+1,求B+A
的值.
22.(10分)已知(x2+mx-3)(2x+n)的计算结果中不含x的一次项,常数项是-6.
(1)求m、n的值;
(2)求(m+n)(m2-mn+n2)的值.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)某高分子聚合材料的性能优于铝合金材料,密度为9×102 kg/m3.又知铝合金的密度约为2.7×103 kg/m3,求铝合金的密度是这种材料密度的多少倍.
24.(10分)(2025吉林期末)如图,在长为(4a-1)m、宽为(3b+2)m的长方形铁片上,挖去一个长为(3a-2)m、宽为2b m的小长方形铁片.
(1)计算剩余部分(即阴影部分)的面积;
(2)当a=4,b=3时,求图中阴影部分的面积.
25.(10分)综合与实践:特值法是解决数学问题的一种常用方法,即通过取题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.综合实践课上田老师展示了如下例题:
例:已知多项式2x3-2x2+m有一个因式是x+1,求m的值.
解:由题意,设2x3-2x2+m=A·(x+1)(A为整式),
由于上式为恒等式,为了方便计算,取x=-1,
则2×(-1)3-2×(-1)2+m=0,解得m=■.
数学思考:(1)“■”处m的值为 ;
方法应用:(2)已知多项式2x3-x2-x+b有一个因式是2x-1,求b的值;
深入探究:(3)若多项式x4+ax3+bx-3有因式(x-1)和(x+2),求a、b的值.
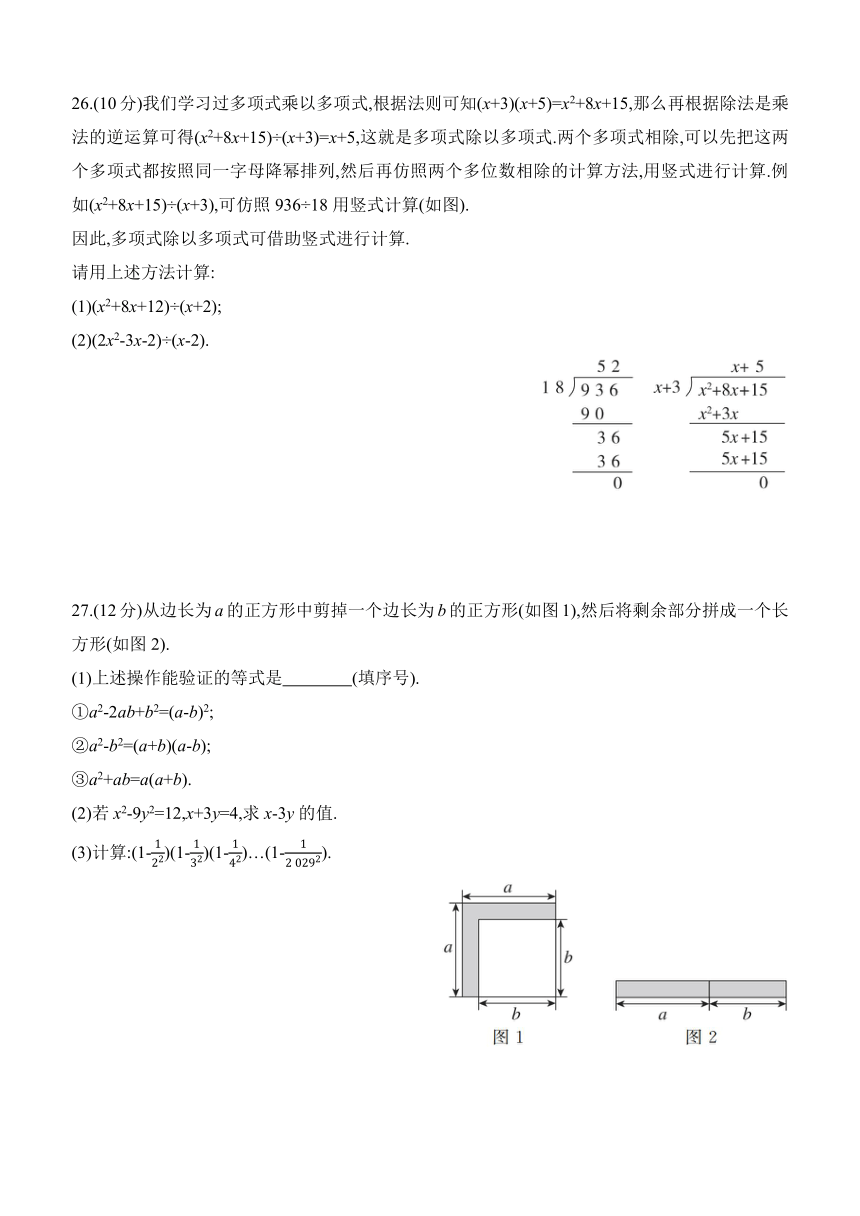
26.(10分)我们学习过多项式乘以多项式,根据法则可知(x+3)(x+5)=x2+8x+15,那么再根据除法是乘法的逆运算可得(x2+8x+15)÷(x+3)=x+5,这就是多项式除以多项式.两个多项式相除,可以先把这两个多项式都按照同一字母降幂排列,然后再仿照两个多位数相除的计算方法,用竖式进行计算.例如(x2+8x+15)÷(x+3),可仿照936÷18用竖式计算(如图).
因此,多项式除以多项式可借助竖式进行计算.
请用上述方法计算:
(1)(x2+8x+12)÷(x+2);
(2)(2x2-3x-2)÷(x-2).
27.(12分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 (填序号).
①a2-2ab+b2=(a-b)2;
②a2-b2=(a+b)(a-b);
③a2+ab=a(a+b).
(2)若x2-9y2=12,x+3y=4,求x-3y的值.
(3)计算:(1-)(1-)(1-)…(1-).
【详解答案】
1.A 解析:(2m2)3
=23m2×3
=8m6.
故选A.
2.D 解析:A.x3+x3=2x3,故此选项不符合题意;B.x3·x9=x12,故此选项不符合题意;C.(x2)3=x6,故此选项不符合题意;D.x3÷x=x2,故此选项符合题意.故选D.
3.B 解析:原式=2x.故选B.
4.B 解析:A.有一项相同(a),另一项互为相反数(2b和-2b),能用平方差公式运算,不符合题意;B.两项均互为相反数,不能用平方差公式运算,符合题意;C.有一项相同(b),另一项互为相反数(2a和-2a),能用平方差公式运算,不符合题意;D.有一项相同(-b),另一项互为相反数(2a和-2a),能用平方差公式运算,不符合题意.故选B.
5.B 解析:A.等号右边不是整式,不符合因式分解的定义,不符合题意;B.符合将多项式分解成几个整式的积的形式,是因式分解,符合题意;C.等号右边不是整式的积的形式,不符合题意;D.等号右边不是整式的积的形式,不符合因式分解的定义,不符合题意.故选B.
6.D 解析:(-)2 025×(-)2 026
=(-)2 025×()2 026
=(-)2 025×
=(-1)2 025×
=-1×
=-.
故选D.
7.A 解析:A.(2 000-1)2=1 9992,故本选项正确;
B.(2 000-1)(2 000+1)=2 0002-1,故本选项错误;
C.(1 999+1)(1 999-1)=1 9992-1,故本选项错误;
D.(1 999+1)2=2 0002,故本选项错误.
故选A.
8.C 解析:A.∵(x+y)2=x2+2xy+y2,-(x+y)2=-(x2+2xy+y2)=-x2-2xy-y2,∴(x+y)2≠-(x+y)2.故本选项不符合题意;B.∵(x-y)2=x2-2xy+y2,(-x-y)2=(-x)2+2·(-x)·(-y)+(-y)2=x2+2xy+y2,∴(x-y)2≠(-x-y)2.故本选项不符合题意;C.∵(x-y)2=x2-2xy+y2, (y-x)2=y2-2xy+x2=x2-2xy+y2,∴(x-y)2=(y-x)2.故本选项符合题意;D.∵-(x-y)2=-(x2-2xy+y2)=-x2+2xy-y2,(y-x)2=y2-2xy+x2=x2-2xy+y2,∴-(x-y)2≠(y-x)2.故本选项不符合题意.故选C.
9.B 解析:∵该长方形的周长为14,面积为10,
∴2(x+y)=14,xy=10,则x+y=7.
∴x2y+xy2=xy(x+y)=10×7=70.
故选B.
10.C 解析:由题图可知,SA=a2,SB=b2,SC=ab,
∵(a+2b)(2a+b)=2a2+5ab+2b2,
∴拼成大长方形需要卡片A的张数为2,B的张数为2,C的张数为5.
故选C.
11.2ab2 解析:多项式8a3b2+6ab3c的公因式是2ab2.
12.-21a3b 解析:原式=-3a2·7ab=-21a3b.
13.(x-2y)2 解析:x2-4xy+4y2=x2-4xy+(2y)2=(x-2y)2.
14.-6 解析:∵a2-b2=12,
∴(a+b)(a-b)=12.
∵a-b=-2,
∴a+b=-6.
15.2 027 解析:∵x2+x-2=0,
∴x2+x=2.
∴x3+2x2-x+2 025
=x3+x2+x2-x+2 025
=x(x2+x)+x2-x+2 025
=2x+x2-x+2 025
=x2+x+2 025
=2+2 025
=2 027.
16.±2 解析:∵x2+y2=10,xy=3,
∴(x-y)2
=x2-2xy+y2
=10-6
=4.
∴x-y=±2.
17.解:(1)(a3x4-0.9ax3)÷ax3
=a3x4÷ax3-0.9ax3÷ax3
=2a2x-.
(2)x(x-2y)+(x+y)2
=x2-2xy+x2+2xy+y2
=2x2+y2.
18.解:(x+1)(x+2)+
=x2+3x+2+
=x2+3x+
=.
19. 解:(1)51×49=(50+1)(50-1)=502-1=2 499.
(2)1052=(100+5)2=1002+1 000+25=11 025.
20.解:[(-y)·(-4y)+(x-2y)2-(3y)2]·2y
=(5y2+x2+4y2-4xy-9y2)·2y
=(x2-4xy)·2y
=2x2y-8xy2,
当x=-3,y=时,原式=2×(-3)2×-8×(-3)×=15.
21.解:由题意可得B=A·(x+1)
=x(x+1),
=x2+x,
所以B+A=x2+x+x=x2+2x.
22.解:(1)原式=2x3+nx2+2mx2+mnx-6x-3n
=2x3+(n+2m)x2+(mn-6)x-3n,
由题意可知mn-6=0,-3n=-6,
解得m=3,n=2.
(2)原式=m3-m2n+mn2+m2n-mn2+n3=m3+n3,
当m=3,n=2时,
原式=33+23
=27+8
=35.
23.解:(2.7×103)÷(9×102)
=(2.7÷9)×(103÷102)
=0.3×10
=3.
答:铝合金的密度是这种材料的密度的3倍.
24.解:(1)剩余部分(即阴影部分)的面积为
(4a-1)(3b+2)-2b(3a-2)=12ab+8a-3b-2-6ab+4b=(6ab+8a+b-2)(m2).
(2)当a=4,b=3时,
阴影部分的面积为6ab+8a+b-2=6×4×3+8×4+3-2=105(m2).
25.解:(1)4
(2)多项式2x3-x2-x+b有一个因式是2x-1,
设2x3-x2-x+b=A·(2x-1)(A为整式),
由于上式为恒等式,为了方便计算,取x=,
则2×+b=0,
解得b=.
(3)设x4+ax3+bx-3=A·(x-1)·(x+2)(A为整式),
由于上式为恒等式,为方便计算,
取x=1,则14+a×13+b×1-3=0,
即a+b=2,
取x=-2,则(-2)4+a×(-2)3+b×(-2)-3=0,
即8a+2b=13,
联立
解得
∴a=,b=.
26.解:(1)(x2+8x+12)÷(x+2).
∴(x2+8x+12)÷(x+2)=x+6.
(2)(2x2-3x-2)÷(x-2).
∴(2x2-3x-2)÷(x-2)=2x+1.
27.解:(1)②
(2)∵x2-9y2=(x+3y)(x-3y)=12,x+3y=4,
∴x-3y=3.
(3)原式=(1-)(1+)(1-)×(1+)(1-)(1+)×…×(1-)(1+)
=×…×
=
=.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.计算(2m2)3的结果为 ( )
A.8m6 B.6m2 C.2m2 D.4m2
2.(2024徐州中考)下列运算正确的是 ( )
A.x3+x3=x6 B.x3·x9=x27
C.(x2)3=x5 D.x3÷x=x2
3.计算6x3÷3x2的结果是 ( )
A.x B.2x C.2x5 D.2x6
4.在进行多项式的乘法运算时,下列式子不能用平方差公式运算的是 ( )
A.(a+2b)(a-2b) B.(a+2b)(-a-2b)
C.(2a+b)(-2a+b) D.(2a-b)(-2a-b)
5.下列等式从左到右变形,是因式分解的是 ( )
A.2a-1=a(2-) B.x2-2x+1=(x-1)2
C.(a-b)(a+b)=a2-b2 D.x2+x+1=x(x+1)+1
6.(-×(-)2 026的计算结果是 ( )
A. B.- C. D.-
7.若用简便方法计算1 9992,应当用下列哪个式子 ( )
A.(2 000-1)2 B.(2 000-1)(2 000+1)
C.(1 999+1)(1 999-1) D.(1 999+1)2
8.下列各式从左到右的变形,正确的是 ( )
A.(x+y)2=-(x+y)2 B.(x-y)2=(-x-y)2
C.(x-y)2=(y-x)2 D.-(x-y)2=(y-x)2
9.如图,长方形的长和宽分别是x、y,它的周长为14,面积为10,则x2y+xy2的值为 ( )
A.140 B.70 C.14 D.10
10.如图,现有三种不同尺寸的卡片,分别是正方形卡片A、正方形卡片B和长方形卡片C.若要拼成一个长为a+2b、宽为2a+b的大长方形,则需要卡片C的张数为 ( )
A.3 B.4 C.5 D.6
二、填空题:本大题共6小题,每小题4分,共24分.
11.多项式8a3b2+6ab3c的公因式是 .
12.计算:3a2·(-7ab)= .
13.(2024常州中考)分解因式:x2-4xy+4y2= .
14.已知a2-b2=12,且a-b=-2,则a+b= .
15.若x2+x-2=0,则x3+2x2-x+2 025的值是 .
16.若x2+y2=10,xy=3,则代数式x-y的值为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
(1)(a3x4-0.9ax3)÷ax3;
(2)x(x-2y)+(x+y)2.
18.(6分)分解因式:(x+1)(x+2)+.
19.(6分)用简便方法计算:
(1)51×49;
(2)1052.
20.(8分)先化简,再求值:[(-y)·(-4y)+(x-2y)2-(3y)2]·2y,其中x=-3,y=.
21.(10分)已知A=x,B是多项式,在计算B+A时,小明把B+A看成B÷A,计算结果是x+1,求B+A
的值.
22.(10分)已知(x2+mx-3)(2x+n)的计算结果中不含x的一次项,常数项是-6.
(1)求m、n的值;
(2)求(m+n)(m2-mn+n2)的值.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)某高分子聚合材料的性能优于铝合金材料,密度为9×102 kg/m3.又知铝合金的密度约为2.7×103 kg/m3,求铝合金的密度是这种材料密度的多少倍.
24.(10分)(2025吉林期末)如图,在长为(4a-1)m、宽为(3b+2)m的长方形铁片上,挖去一个长为(3a-2)m、宽为2b m的小长方形铁片.
(1)计算剩余部分(即阴影部分)的面积;
(2)当a=4,b=3时,求图中阴影部分的面积.
25.(10分)综合与实践:特值法是解决数学问题的一种常用方法,即通过取题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.综合实践课上田老师展示了如下例题:
例:已知多项式2x3-2x2+m有一个因式是x+1,求m的值.
解:由题意,设2x3-2x2+m=A·(x+1)(A为整式),
由于上式为恒等式,为了方便计算,取x=-1,
则2×(-1)3-2×(-1)2+m=0,解得m=■.
数学思考:(1)“■”处m的值为 ;
方法应用:(2)已知多项式2x3-x2-x+b有一个因式是2x-1,求b的值;
深入探究:(3)若多项式x4+ax3+bx-3有因式(x-1)和(x+2),求a、b的值.
26.(10分)我们学习过多项式乘以多项式,根据法则可知(x+3)(x+5)=x2+8x+15,那么再根据除法是乘法的逆运算可得(x2+8x+15)÷(x+3)=x+5,这就是多项式除以多项式.两个多项式相除,可以先把这两个多项式都按照同一字母降幂排列,然后再仿照两个多位数相除的计算方法,用竖式进行计算.例如(x2+8x+15)÷(x+3),可仿照936÷18用竖式计算(如图).
因此,多项式除以多项式可借助竖式进行计算.
请用上述方法计算:
(1)(x2+8x+12)÷(x+2);
(2)(2x2-3x-2)÷(x-2).
27.(12分)从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 (填序号).
①a2-2ab+b2=(a-b)2;
②a2-b2=(a+b)(a-b);
③a2+ab=a(a+b).
(2)若x2-9y2=12,x+3y=4,求x-3y的值.
(3)计算:(1-)(1-)(1-)…(1-).
【详解答案】
1.A 解析:(2m2)3
=23m2×3
=8m6.
故选A.
2.D 解析:A.x3+x3=2x3,故此选项不符合题意;B.x3·x9=x12,故此选项不符合题意;C.(x2)3=x6,故此选项不符合题意;D.x3÷x=x2,故此选项符合题意.故选D.
3.B 解析:原式=2x.故选B.
4.B 解析:A.有一项相同(a),另一项互为相反数(2b和-2b),能用平方差公式运算,不符合题意;B.两项均互为相反数,不能用平方差公式运算,符合题意;C.有一项相同(b),另一项互为相反数(2a和-2a),能用平方差公式运算,不符合题意;D.有一项相同(-b),另一项互为相反数(2a和-2a),能用平方差公式运算,不符合题意.故选B.
5.B 解析:A.等号右边不是整式,不符合因式分解的定义,不符合题意;B.符合将多项式分解成几个整式的积的形式,是因式分解,符合题意;C.等号右边不是整式的积的形式,不符合题意;D.等号右边不是整式的积的形式,不符合因式分解的定义,不符合题意.故选B.
6.D 解析:(-)2 025×(-)2 026
=(-)2 025×()2 026
=(-)2 025×
=(-1)2 025×
=-1×
=-.
故选D.
7.A 解析:A.(2 000-1)2=1 9992,故本选项正确;
B.(2 000-1)(2 000+1)=2 0002-1,故本选项错误;
C.(1 999+1)(1 999-1)=1 9992-1,故本选项错误;
D.(1 999+1)2=2 0002,故本选项错误.
故选A.
8.C 解析:A.∵(x+y)2=x2+2xy+y2,-(x+y)2=-(x2+2xy+y2)=-x2-2xy-y2,∴(x+y)2≠-(x+y)2.故本选项不符合题意;B.∵(x-y)2=x2-2xy+y2,(-x-y)2=(-x)2+2·(-x)·(-y)+(-y)2=x2+2xy+y2,∴(x-y)2≠(-x-y)2.故本选项不符合题意;C.∵(x-y)2=x2-2xy+y2, (y-x)2=y2-2xy+x2=x2-2xy+y2,∴(x-y)2=(y-x)2.故本选项符合题意;D.∵-(x-y)2=-(x2-2xy+y2)=-x2+2xy-y2,(y-x)2=y2-2xy+x2=x2-2xy+y2,∴-(x-y)2≠(y-x)2.故本选项不符合题意.故选C.
9.B 解析:∵该长方形的周长为14,面积为10,
∴2(x+y)=14,xy=10,则x+y=7.
∴x2y+xy2=xy(x+y)=10×7=70.
故选B.
10.C 解析:由题图可知,SA=a2,SB=b2,SC=ab,
∵(a+2b)(2a+b)=2a2+5ab+2b2,
∴拼成大长方形需要卡片A的张数为2,B的张数为2,C的张数为5.
故选C.
11.2ab2 解析:多项式8a3b2+6ab3c的公因式是2ab2.
12.-21a3b 解析:原式=-3a2·7ab=-21a3b.
13.(x-2y)2 解析:x2-4xy+4y2=x2-4xy+(2y)2=(x-2y)2.
14.-6 解析:∵a2-b2=12,
∴(a+b)(a-b)=12.
∵a-b=-2,
∴a+b=-6.
15.2 027 解析:∵x2+x-2=0,
∴x2+x=2.
∴x3+2x2-x+2 025
=x3+x2+x2-x+2 025
=x(x2+x)+x2-x+2 025
=2x+x2-x+2 025
=x2+x+2 025
=2+2 025
=2 027.
16.±2 解析:∵x2+y2=10,xy=3,
∴(x-y)2
=x2-2xy+y2
=10-6
=4.
∴x-y=±2.
17.解:(1)(a3x4-0.9ax3)÷ax3
=a3x4÷ax3-0.9ax3÷ax3
=2a2x-.
(2)x(x-2y)+(x+y)2
=x2-2xy+x2+2xy+y2
=2x2+y2.
18.解:(x+1)(x+2)+
=x2+3x+2+
=x2+3x+
=.
19. 解:(1)51×49=(50+1)(50-1)=502-1=2 499.
(2)1052=(100+5)2=1002+1 000+25=11 025.
20.解:[(-y)·(-4y)+(x-2y)2-(3y)2]·2y
=(5y2+x2+4y2-4xy-9y2)·2y
=(x2-4xy)·2y
=2x2y-8xy2,
当x=-3,y=时,原式=2×(-3)2×-8×(-3)×=15.
21.解:由题意可得B=A·(x+1)
=x(x+1),
=x2+x,
所以B+A=x2+x+x=x2+2x.
22.解:(1)原式=2x3+nx2+2mx2+mnx-6x-3n
=2x3+(n+2m)x2+(mn-6)x-3n,
由题意可知mn-6=0,-3n=-6,
解得m=3,n=2.
(2)原式=m3-m2n+mn2+m2n-mn2+n3=m3+n3,
当m=3,n=2时,
原式=33+23
=27+8
=35.
23.解:(2.7×103)÷(9×102)
=(2.7÷9)×(103÷102)
=0.3×10
=3.
答:铝合金的密度是这种材料的密度的3倍.
24.解:(1)剩余部分(即阴影部分)的面积为
(4a-1)(3b+2)-2b(3a-2)=12ab+8a-3b-2-6ab+4b=(6ab+8a+b-2)(m2).
(2)当a=4,b=3时,
阴影部分的面积为6ab+8a+b-2=6×4×3+8×4+3-2=105(m2).
25.解:(1)4
(2)多项式2x3-x2-x+b有一个因式是2x-1,
设2x3-x2-x+b=A·(2x-1)(A为整式),
由于上式为恒等式,为了方便计算,取x=,
则2×+b=0,
解得b=.
(3)设x4+ax3+bx-3=A·(x-1)·(x+2)(A为整式),
由于上式为恒等式,为方便计算,
取x=1,则14+a×13+b×1-3=0,
即a+b=2,
取x=-2,则(-2)4+a×(-2)3+b×(-2)-3=0,
即8a+2b=13,
联立
解得
∴a=,b=.
26.解:(1)(x2+8x+12)÷(x+2).
∴(x2+8x+12)÷(x+2)=x+6.
(2)(2x2-3x-2)÷(x-2).
∴(2x2-3x-2)÷(x-2)=2x+1.
27.解:(1)②
(2)∵x2-9y2=(x+3y)(x-3y)=12,x+3y=4,
∴x-3y=3.
(3)原式=(1-)(1+)(1-)×(1+)(1-)(1+)×…×(1-)(1+)
=×…×
=
=.
