第13章勾股定理 评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册
文档属性
| 名称 | 第13章勾股定理 评估测试卷 (含答案)2025-2026学年数学华东师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 368.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 16:01:36 | ||
图片预览



文档简介
第13章 勾股定理 评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各组数中,是勾股数的是 ( )
A.1,2,3 B.5,12,13
C.0.3,0.4,0.5 D.4,6,8
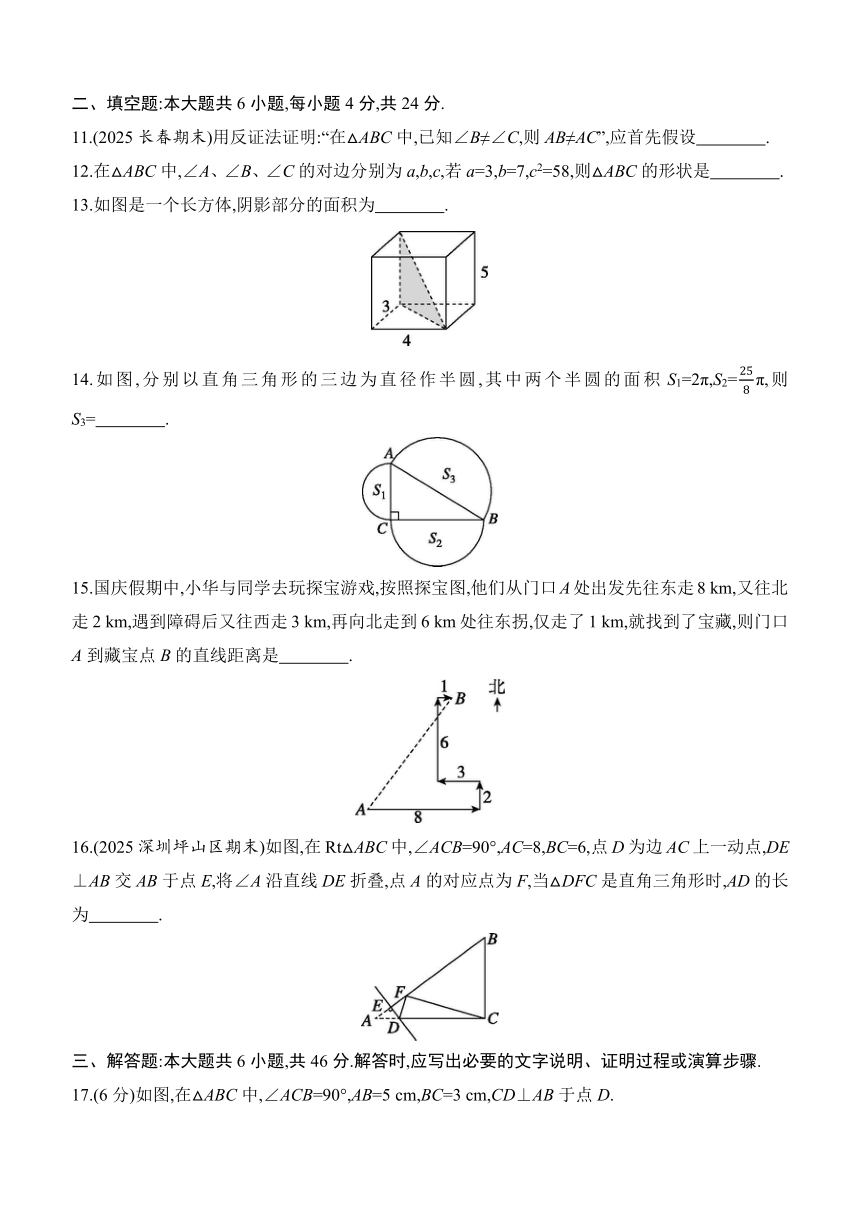
2.如图,网格中每个小正方形的边长均为1,点A、B、C都在格点上,以A为圆心,AB长为半径画弧,交最上方的网格线于点D,则CD的长为 ( )
A. B. C.2.2 D.3-
3.如图是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是 ( )
A.16 B.25 C.144 D.169
4.(2025上海普陀区期末)如图,在7×7的正方形网格中,每个小正方形的边长都为1,点A、B、C、D、E、F均在格点上,那么和线段AB两个端点距离相等的点的轨迹是 ( )
A.直线CD B.直线CE C.直线DE D.直线DF
5.赵爽弦图是一个以勾股形之弦为边的正方形.图中包含四个全等的勾股形和一个小正方形,其面积称为朱实和黄实.如图,设每一个勾股形的两条直角边长分别为a和b,若ab=8,且a2+b2=25,则黄实为 ( )
A.36 B.25 C.16 D.9
6.如图,在5×5的正方形网格中,每个小正方形的边长都为1,从在格点上的点A、B、C、D中任取三点,所构成三角形不是直角三角形的是 ( )
A.△ABD B.△ADC
C.△BCD D.△ABC
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 其大意:如图,推开双门(大小相同),双门间隙CD=2寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),则AB的长是 ( )
A.26寸 B.50.5寸
C.52寸 D.101寸
8.如图,三级台阶,每一级的长、宽、高分别为8 dm、3 dm、2 dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为 ( )
A.15 dm B.17 dm
C.20 dm D.25 dm
9.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,则由下列条件:①∠A-∠B=∠C;②∠A∶∠B∶∠C=1∶3∶4;③a2=b2-c2;④a∶b∶c=1∶.能判定△ABC为直角三角形的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在Rt△ABC中,∠C=90°,BC=15 cm,AB=17 cm,以AC为边作正方形ADEC,则△ABE的面积为 ( )
A.30 cm2 B.28 cm2 C.20 cm2 D.16 cm2
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2025长春期末)用反证法证明:“在△ABC中,已知∠B≠∠C,则AB≠AC”,应首先假设 .
12.在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,若a=3,b=7,c2=58,则△ABC的形状是 .
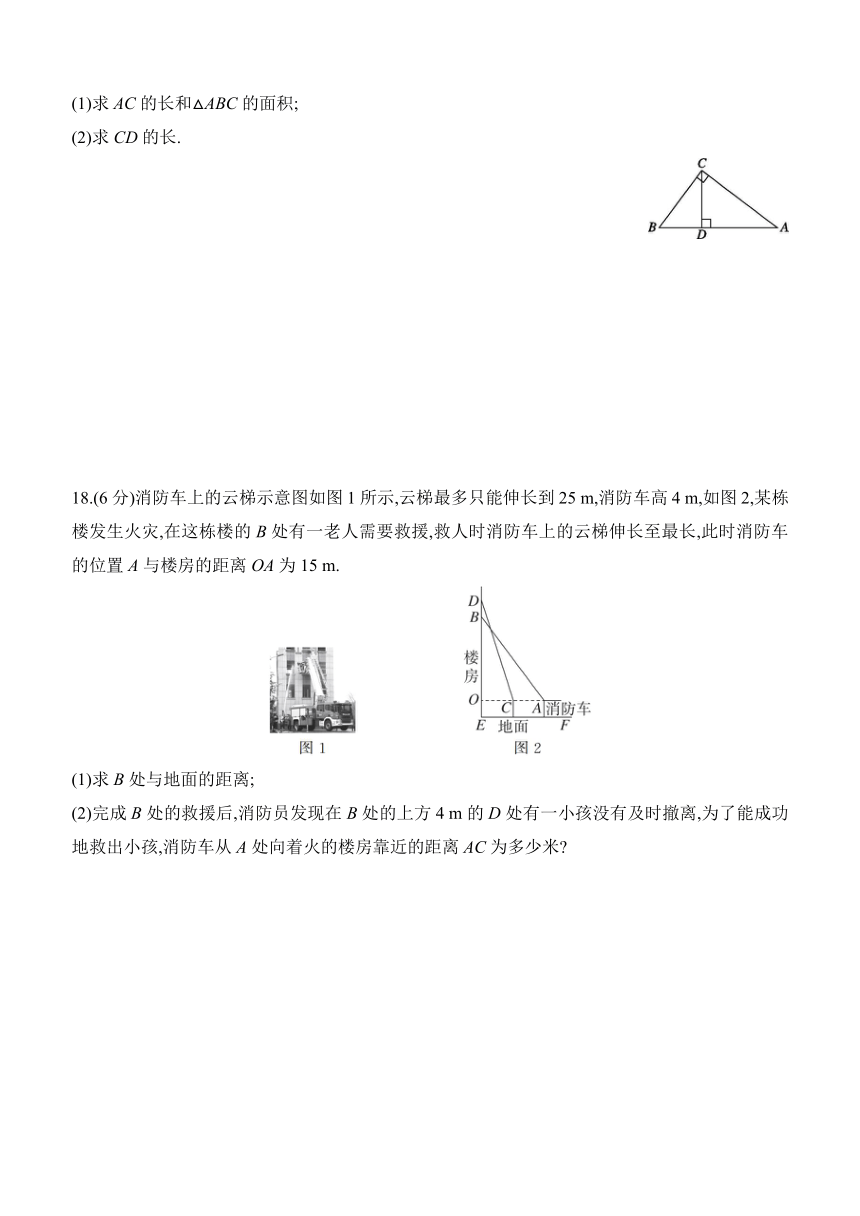
13.如图是一个长方体,阴影部分的面积为 .
14.如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=2π,S2=π,则S3= .
15.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8 km,又往北走2 km,遇到障碍后又往西走3 km,再向北走到6 km处往东拐,仅走了1 km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
16.(2025深圳坪山区期末)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D.
(1)求AC的长和△ABC的面积;
(2)求CD的长.
18.(6分)消防车上的云梯示意图如图1所示,云梯最多只能伸长到25 m,消防车高4 m,如图2,某栋楼发生火灾,在这栋楼的B处有一老人需要救援,救人时消防车上的云梯伸长至最长,此时消防车的位置A与楼房的距离OA为15 m.
(1)求B处与地面的距离;
(2)完成B处的救援后,消防员发现在B处的上方4 m的D处有一小孩没有及时撤离,为了能成功地救出小孩,消防车从A处向着火的楼房靠近的距离AC为多少米
19.(6分)如图,在△ABC中,D、E分别是AC、AB的中点,且BD≠CE.
求证:AB≠AC.
20.(8分)请你在方格纸上按照如下要求设计直角三角形.
(1)使它的三边中有一边边长不是有理数;
(2)使它的三边中有两边边长不是有理数;
(3)使它的三边边长都不是有理数.
21.(10分)如图,在△ABC中,∠ACB=90°,AC=12,BC=5,将△ABC沿直线AB向右平移得到△DEF,若AE=22,BD=4.
(1)求△ABC向右平移的距离;
(2)求四边形AEFC的周长.
22.(10分)如图,已知AB=AC,且AB⊥AC,点D在BC上.
求证:BD2+CD2=2AD2.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图1是用硬纸片做成的两个全等的直角三角形,两条直角边长分别为a和b,斜边长为c;图2是以c为直角边的等腰直角三角形.请你开动脑筋,将图1和图2的三个图形拼成一个能验证勾股定理的图形.请画出拼成的这个图形的示意图,并用它验证勾股定理.
24.(10分)(2025沈阳铁西区期末)如图,把△ABC沿边AB所在直线折叠得到△ABD,点D是点C的对应点,过点A作AE⊥DB于点E,过点C作CF⊥DB交DB的延长线于点F.
(1)若∠ABC=70°,求∠BCF的度数;
(2)若DE=CF=4,EF=2DE,求BE的长.
25.(10分)如图,在五边形ABCDE中,AB⊥BC,AE⊥ED.已知BC=9,AB=12,AE=15,ED=CD=8.
(1)求证:△ACD是直角三角形;
(2)求五边形ABCDE的面积.
26.(10分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3,4,5;5,12,13;7,24,25;9,40,41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数: .
(2)若第一个数用字母n(n为奇数,且n≥3)表示,则后两个数用含n的代数式表示分别为 ,请用所学知识证明它们是一组勾股数.
27.(12分)如图,在△ABC中,∠ABC=90°,AC=25,BC=15.
(1)设点P在AB上,若∠PAC=∠PCA.求AP的长;
(2)设点M在AC上,若△MBC为等腰三角形,求AM的长.
【详解答案】
1.B 解析:A.32=9≠12+22,不是勾股数,不符合题意;B.52+122=132,是勾股数,符合题意;C.不是正整数,不是勾股数,不符合题意;D.42+62=52≠64=82,不是勾股数,不符合题意.故选B.
2. B 解析:如图,连结AD,
由题意知:AD=AB=3,
在Rt△ACD中,由勾股定理,得
CD=.
故选B.
3.B 解析:如图所示,
根据勾股定理得出:
AB==5,
∴EF=AB=5.
∴阴影部分的面积是25.故选B.
4.C 解析:如图,连结AD、BD、AE、BE,
由勾股定理,得AD=BD=,BE==5,
∴AE=BE=5.
∴D和E在线段AB的垂直平分线上,∴和线段AB两个端点距离相等的点的轨迹是直线DE.故选C.
5.D 解析:设大正方形的边长为c,则大正方形的面积为c2,根据勾股定理,得a2+b2=c2,
∵a2+b2=25,
∴c2=25.
∴黄实为c2-4×ab=25-4××8=9.
故选D.
6.C 解析:∵AB2=5,BD2=5,CD2=10,AC2=20,AD2=10,BC2=25,
∴AB2+BD2=AD2,AD2+CD2=AC2,BD2+DC2≠BC2,AB2+AC2=BC2.
∴△BCD不是直角三角形.
故选C.
7.D 解析:如图,取AB的中点为O,则EF的中点也为O,
根据题意可知:CD=EF=2寸,
∴EO=EF=1寸.
设AE=x寸,则AC=AO=(x+1)寸,
∵AE2+CE2=AC2,CE=DF=1尺=10寸,
∴x2+102=(x+1)2.
解得x=49.5.
∴AB=49.5+49.5+2=101(寸).
故选D.
8.B 解析:如图,三级台阶平面展开图为长方形,宽为8 dm,长为(2+3)×3 dm,
则蚂蚁沿台阶面爬行到点B的最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点B的最短路程为x dm,
由勾股定理,得x2=82+[(2+3)×3]2=172,
解得x=17.
故选B.
9.D 解析:∵∠A-∠B=∠C,
∴∠A=∠C+∠B.
∴∠A+∠A=180°.
∴∠A=90°.
∴△ABC为直角三角形,正确.故①符合题意;
∵∠A∶∠B∶∠C=1∶3∶4,
∴∠C=×180°=90°.
∴△ABC为直角三角形,正确.故②符合题意;
∵a2=b2-c2,
∴a2+c2=b2.
∴△ABC为直角三角形,正确.故③符合题意;
∵a∶b∶c=1∶,
∴a2+b2=c2,
∴△ABC为直角三角形,正确.故④符合题意.综上可知,①②③④能判定△ABC为直角三角形,共4个.故选D.
10.B 解析:在Rt△ABC中,BC=15 cm,AB=17 cm,
∴AC==8(cm).
∵四边形ADEC是正方形,
∴S△ACE=S正方形ADEC=×8×8=32(cm2).
∵BC=15 cm,AC=8 cm,
∴S△ABC=AC·BC=×8×15=60(cm2).
∴S△ABE=60-32=28(cm2).
故选B.
11.AB=AC 解析:反证法证明:“在△ABC中,已知∠B≠∠C,则AB≠AC”,应首先假设AB=AC.
12.直角三角形
13. 解析:如图所示,BC==5,
∴阴影部分的面积为AB·BC=×5×5=.
14.π 解析:根据勾股定理,得AB2=AC2+BC2,
∴S3=S1+S2=+2π=π.
15.10 km 解析:如图,过点B作BC⊥AC,垂足为C,延长ND交AC于点M.
观察图形可知AC=AF-MF+MC=8-3+1=6(km),BC=NM=ND+DM=6+2=8(km),
在Rt△ACB中,AB==10(km).
故门口A到藏宝点B的直线距离是10 km.
16.或 解析:当∠DFC=90°时,
∵将∠A沿直线DE折叠,点A的对应点为F.
∴∠A=∠AFD,AD=DF.
∵∠ACB=90°,∠DFC=90°,
∴∠A+∠B=90°,∠AFD+∠BFC=90°.
∴∠BFC=∠B.
∴CF=BC=6.
在Rt△DFC中,CD2=DF2+CF2,
∴(8-AD)2=AD2+36,
∴AD=;
当点F与点B重合时,AD=DF,如图,
∵DF2=CF2+CD2,
∴AD2=(8-AD)2+36,
∴AD=.
综上所述,AD的长为或.
17.解:(1)在Rt△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,
∴AC==4(cm),
∴AC·BC=×4×3=6(cm2).
(2)∵CD⊥AB,
∴AC·BC=AB·CD.
∴CD==2.4(cm).
18.解:(1)在Rt△OAB中,
∵AB=25 m,OA=15 m,OE=4 m,
∴OB==20(m).
∴BE=OB+OE=20+4=24(m).
答:B处与地面的距离是24 m.
(2)由题意,得BD=4 m,
∵CD=25 m,OD=OB+BD=20+4=24(m),
∴OC==7(m).
∴AC=OA-OC=15-7=8(m).
答:消防车从A处向着火的楼房靠近的距离AC为8 m.
19. 证明:设AB=AC,则∠ABC=∠ACB,
∵AB=AC,D、E分别是AC、AB的中点,
∴BE=CD.
在△BCD和△CBE中,
∴△BCD≌△CBE(SAS).
∴BD=CE,与BD≠CE相矛盾.
∴AB≠AC.
20.解:如图.
(1)△ABC是所求作的三角形.
(2)△PHG是所求作的三角形.
(3)△DEF是所求作的三角形.
(答案不唯一)
21.解:(1)在△ABC中,∠ACB=90°,AC=12,BC=5,
由勾股定理,得AB==13.
∵AE=22,∴BE=22-13=9,
∴△ABC向右平移的距离为9.
(2)由平移的性质可知CF=BE=9,EF=BC=5,
∴四边形AEFC的周长=AC+AE+EF+CF=12+22+5+9=48.
22.证明:作AE⊥BC于点E,如图所示.
∵AB=AC,且AB⊥AC,
∴△ABC是等腰直角三角形.
∵AE⊥BC,
∴BE=AE=EC.
∴BD=BE-DE=AE-DE,CD=EC+DE=AE+DE.
∴BD2+CD2
=(AE-DE)2+(AE+DE)2
=AE2+DE2-2AE·DE+AE2+DE2+2AE·DE
=2AE2+2DE2
=2(AE2+DE2)
=2AD2.
23.解:将三个三角形拼成直角梯形,如图所示.
验证:
∵梯形的面积为(a+b)(a+b)或ab+ab+c2,
即(a+b)(a+b)=ab+ab+c2,
∴a2+b2=c2.
24.解:(1)∵把△ABC沿边AB所在直线折叠得到△ABD,
∴∠ABD=∠ABC=70°.
∴∠CBF=180°-∠ABD-∠ABC=180°-70°-70°=40°.
∵CF⊥DB交DB的延长线于点F,
∴∠F=90°.
∴∠BCF=90°-∠CBF=90°-40°=50°.
∴∠BCF的度数是50°.
(2)∵DE=CF=4,EF=2DE,
∴BD=4+BE,EF=8.
∴BF=8-BE.
由折叠,得BD=BC=4+BE,
∵CF2+BF2=BC2,
∴42+(8-BE)2=(4+BE)2.
解得BE=,
∴BE的长是.
25.(1)证明:∵AB⊥BC,AE⊥ED,BC=9,AB=12,AE=15,ED=CD=8,
∴∠B=∠E=90°.
∴AC==15,AD==17.
∵AC2+CD2=152+82=289,AD2=172=289,
∴AC2+CD2=AD2.
∴∠ACD=90°.
∴△ACD是直角三角形.
(2)解:×12×9+×15×8+×15×8=174,
∴五边形ABCDE的面积是174.
26.解:(1)11,60,61
(2)和
证明如下:
∵n2+=n2+=
,
,
∴n2+.
由题意知,n,,三个数均为正整数,
∴n,,三个数是一组勾股数.
27.解:(1)∵∠ABC=90°,AC=25,BC=15,
∴AB==20.
∵∠PAC=∠PCA,
∴AP=PC.
设AP=PC=x,
则PB=20-x.
在Rt△PBC中,由勾股定理,得PB2+BC2=PC2,∴(20-x)2+152=x2,
解得x=,∴AP=.
(2)当CM=BC=15时,△MBC为等腰三角形,
∴AM=AC-CM=10;
当BM=BC=15时,△MBC为等腰三角形,
如图,过点B作BH⊥AC于点H,
则BH==12.
∴CH==9.
∴AM=AC-2CH=7;
当BM=CM时,△MBC为等腰三角形,
连结BM,
设AM=x,则BM=CM=25-x,
∴(25-x)2=122+(25-x-9)2.
解得x=12.5.
∴AM=12.5.
综上所述,AM的长为10或7或12.5.
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各组数中,是勾股数的是 ( )
A.1,2,3 B.5,12,13
C.0.3,0.4,0.5 D.4,6,8
2.如图,网格中每个小正方形的边长均为1,点A、B、C都在格点上,以A为圆心,AB长为半径画弧,交最上方的网格线于点D,则CD的长为 ( )
A. B. C.2.2 D.3-
3.如图是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是 ( )
A.16 B.25 C.144 D.169
4.(2025上海普陀区期末)如图,在7×7的正方形网格中,每个小正方形的边长都为1,点A、B、C、D、E、F均在格点上,那么和线段AB两个端点距离相等的点的轨迹是 ( )
A.直线CD B.直线CE C.直线DE D.直线DF
5.赵爽弦图是一个以勾股形之弦为边的正方形.图中包含四个全等的勾股形和一个小正方形,其面积称为朱实和黄实.如图,设每一个勾股形的两条直角边长分别为a和b,若ab=8,且a2+b2=25,则黄实为 ( )
A.36 B.25 C.16 D.9
6.如图,在5×5的正方形网格中,每个小正方形的边长都为1,从在格点上的点A、B、C、D中任取三点,所构成三角形不是直角三角形的是 ( )
A.△ABD B.△ADC
C.△BCD D.△ABC
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 其大意:如图,推开双门(大小相同),双门间隙CD=2寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),则AB的长是 ( )
A.26寸 B.50.5寸
C.52寸 D.101寸
8.如图,三级台阶,每一级的长、宽、高分别为8 dm、3 dm、2 dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为 ( )
A.15 dm B.17 dm
C.20 dm D.25 dm
9.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,则由下列条件:①∠A-∠B=∠C;②∠A∶∠B∶∠C=1∶3∶4;③a2=b2-c2;④a∶b∶c=1∶.能判定△ABC为直角三角形的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在Rt△ABC中,∠C=90°,BC=15 cm,AB=17 cm,以AC为边作正方形ADEC,则△ABE的面积为 ( )
A.30 cm2 B.28 cm2 C.20 cm2 D.16 cm2
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2025长春期末)用反证法证明:“在△ABC中,已知∠B≠∠C,则AB≠AC”,应首先假设 .
12.在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,若a=3,b=7,c2=58,则△ABC的形状是 .
13.如图是一个长方体,阴影部分的面积为 .
14.如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=2π,S2=π,则S3= .
15.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8 km,又往北走2 km,遇到障碍后又往西走3 km,再向北走到6 km处往东拐,仅走了1 km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
16.(2025深圳坪山区期末)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,在△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,CD⊥AB于点D.
(1)求AC的长和△ABC的面积;
(2)求CD的长.
18.(6分)消防车上的云梯示意图如图1所示,云梯最多只能伸长到25 m,消防车高4 m,如图2,某栋楼发生火灾,在这栋楼的B处有一老人需要救援,救人时消防车上的云梯伸长至最长,此时消防车的位置A与楼房的距离OA为15 m.
(1)求B处与地面的距离;
(2)完成B处的救援后,消防员发现在B处的上方4 m的D处有一小孩没有及时撤离,为了能成功地救出小孩,消防车从A处向着火的楼房靠近的距离AC为多少米
19.(6分)如图,在△ABC中,D、E分别是AC、AB的中点,且BD≠CE.
求证:AB≠AC.
20.(8分)请你在方格纸上按照如下要求设计直角三角形.
(1)使它的三边中有一边边长不是有理数;
(2)使它的三边中有两边边长不是有理数;
(3)使它的三边边长都不是有理数.
21.(10分)如图,在△ABC中,∠ACB=90°,AC=12,BC=5,将△ABC沿直线AB向右平移得到△DEF,若AE=22,BD=4.
(1)求△ABC向右平移的距离;
(2)求四边形AEFC的周长.
22.(10分)如图,已知AB=AC,且AB⊥AC,点D在BC上.
求证:BD2+CD2=2AD2.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图1是用硬纸片做成的两个全等的直角三角形,两条直角边长分别为a和b,斜边长为c;图2是以c为直角边的等腰直角三角形.请你开动脑筋,将图1和图2的三个图形拼成一个能验证勾股定理的图形.请画出拼成的这个图形的示意图,并用它验证勾股定理.
24.(10分)(2025沈阳铁西区期末)如图,把△ABC沿边AB所在直线折叠得到△ABD,点D是点C的对应点,过点A作AE⊥DB于点E,过点C作CF⊥DB交DB的延长线于点F.
(1)若∠ABC=70°,求∠BCF的度数;
(2)若DE=CF=4,EF=2DE,求BE的长.
25.(10分)如图,在五边形ABCDE中,AB⊥BC,AE⊥ED.已知BC=9,AB=12,AE=15,ED=CD=8.
(1)求证:△ACD是直角三角形;
(2)求五边形ABCDE的面积.
26.(10分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3,4,5;5,12,13;7,24,25;9,40,41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数: .
(2)若第一个数用字母n(n为奇数,且n≥3)表示,则后两个数用含n的代数式表示分别为 ,请用所学知识证明它们是一组勾股数.
27.(12分)如图,在△ABC中,∠ABC=90°,AC=25,BC=15.
(1)设点P在AB上,若∠PAC=∠PCA.求AP的长;
(2)设点M在AC上,若△MBC为等腰三角形,求AM的长.
【详解答案】
1.B 解析:A.32=9≠12+22,不是勾股数,不符合题意;B.52+122=132,是勾股数,符合题意;C.不是正整数,不是勾股数,不符合题意;D.42+62=52≠64=82,不是勾股数,不符合题意.故选B.
2. B 解析:如图,连结AD,
由题意知:AD=AB=3,
在Rt△ACD中,由勾股定理,得
CD=.
故选B.
3.B 解析:如图所示,
根据勾股定理得出:
AB==5,
∴EF=AB=5.
∴阴影部分的面积是25.故选B.
4.C 解析:如图,连结AD、BD、AE、BE,
由勾股定理,得AD=BD=,BE==5,
∴AE=BE=5.
∴D和E在线段AB的垂直平分线上,∴和线段AB两个端点距离相等的点的轨迹是直线DE.故选C.
5.D 解析:设大正方形的边长为c,则大正方形的面积为c2,根据勾股定理,得a2+b2=c2,
∵a2+b2=25,
∴c2=25.
∴黄实为c2-4×ab=25-4××8=9.
故选D.
6.C 解析:∵AB2=5,BD2=5,CD2=10,AC2=20,AD2=10,BC2=25,
∴AB2+BD2=AD2,AD2+CD2=AC2,BD2+DC2≠BC2,AB2+AC2=BC2.
∴△BCD不是直角三角形.
故选C.
7.D 解析:如图,取AB的中点为O,则EF的中点也为O,
根据题意可知:CD=EF=2寸,
∴EO=EF=1寸.
设AE=x寸,则AC=AO=(x+1)寸,
∵AE2+CE2=AC2,CE=DF=1尺=10寸,
∴x2+102=(x+1)2.
解得x=49.5.
∴AB=49.5+49.5+2=101(寸).
故选D.
8.B 解析:如图,三级台阶平面展开图为长方形,宽为8 dm,长为(2+3)×3 dm,
则蚂蚁沿台阶面爬行到点B的最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点B的最短路程为x dm,
由勾股定理,得x2=82+[(2+3)×3]2=172,
解得x=17.
故选B.
9.D 解析:∵∠A-∠B=∠C,
∴∠A=∠C+∠B.
∴∠A+∠A=180°.
∴∠A=90°.
∴△ABC为直角三角形,正确.故①符合题意;
∵∠A∶∠B∶∠C=1∶3∶4,
∴∠C=×180°=90°.
∴△ABC为直角三角形,正确.故②符合题意;
∵a2=b2-c2,
∴a2+c2=b2.
∴△ABC为直角三角形,正确.故③符合题意;
∵a∶b∶c=1∶,
∴a2+b2=c2,
∴△ABC为直角三角形,正确.故④符合题意.综上可知,①②③④能判定△ABC为直角三角形,共4个.故选D.
10.B 解析:在Rt△ABC中,BC=15 cm,AB=17 cm,
∴AC==8(cm).
∵四边形ADEC是正方形,
∴S△ACE=S正方形ADEC=×8×8=32(cm2).
∵BC=15 cm,AC=8 cm,
∴S△ABC=AC·BC=×8×15=60(cm2).
∴S△ABE=60-32=28(cm2).
故选B.
11.AB=AC 解析:反证法证明:“在△ABC中,已知∠B≠∠C,则AB≠AC”,应首先假设AB=AC.
12.直角三角形
13. 解析:如图所示,BC==5,
∴阴影部分的面积为AB·BC=×5×5=.
14.π 解析:根据勾股定理,得AB2=AC2+BC2,
∴S3=S1+S2=+2π=π.
15.10 km 解析:如图,过点B作BC⊥AC,垂足为C,延长ND交AC于点M.
观察图形可知AC=AF-MF+MC=8-3+1=6(km),BC=NM=ND+DM=6+2=8(km),
在Rt△ACB中,AB==10(km).
故门口A到藏宝点B的直线距离是10 km.
16.或 解析:当∠DFC=90°时,
∵将∠A沿直线DE折叠,点A的对应点为F.
∴∠A=∠AFD,AD=DF.
∵∠ACB=90°,∠DFC=90°,
∴∠A+∠B=90°,∠AFD+∠BFC=90°.
∴∠BFC=∠B.
∴CF=BC=6.
在Rt△DFC中,CD2=DF2+CF2,
∴(8-AD)2=AD2+36,
∴AD=;
当点F与点B重合时,AD=DF,如图,
∵DF2=CF2+CD2,
∴AD2=(8-AD)2+36,
∴AD=.
综上所述,AD的长为或.
17.解:(1)在Rt△ABC中,∠ACB=90°,AB=5 cm,BC=3 cm,
∴AC==4(cm),
∴AC·BC=×4×3=6(cm2).
(2)∵CD⊥AB,
∴AC·BC=AB·CD.
∴CD==2.4(cm).
18.解:(1)在Rt△OAB中,
∵AB=25 m,OA=15 m,OE=4 m,
∴OB==20(m).
∴BE=OB+OE=20+4=24(m).
答:B处与地面的距离是24 m.
(2)由题意,得BD=4 m,
∵CD=25 m,OD=OB+BD=20+4=24(m),
∴OC==7(m).
∴AC=OA-OC=15-7=8(m).
答:消防车从A处向着火的楼房靠近的距离AC为8 m.
19. 证明:设AB=AC,则∠ABC=∠ACB,
∵AB=AC,D、E分别是AC、AB的中点,
∴BE=CD.
在△BCD和△CBE中,
∴△BCD≌△CBE(SAS).
∴BD=CE,与BD≠CE相矛盾.
∴AB≠AC.
20.解:如图.
(1)△ABC是所求作的三角形.
(2)△PHG是所求作的三角形.
(3)△DEF是所求作的三角形.
(答案不唯一)
21.解:(1)在△ABC中,∠ACB=90°,AC=12,BC=5,
由勾股定理,得AB==13.
∵AE=22,∴BE=22-13=9,
∴△ABC向右平移的距离为9.
(2)由平移的性质可知CF=BE=9,EF=BC=5,
∴四边形AEFC的周长=AC+AE+EF+CF=12+22+5+9=48.
22.证明:作AE⊥BC于点E,如图所示.
∵AB=AC,且AB⊥AC,
∴△ABC是等腰直角三角形.
∵AE⊥BC,
∴BE=AE=EC.
∴BD=BE-DE=AE-DE,CD=EC+DE=AE+DE.
∴BD2+CD2
=(AE-DE)2+(AE+DE)2
=AE2+DE2-2AE·DE+AE2+DE2+2AE·DE
=2AE2+2DE2
=2(AE2+DE2)
=2AD2.
23.解:将三个三角形拼成直角梯形,如图所示.
验证:
∵梯形的面积为(a+b)(a+b)或ab+ab+c2,
即(a+b)(a+b)=ab+ab+c2,
∴a2+b2=c2.
24.解:(1)∵把△ABC沿边AB所在直线折叠得到△ABD,
∴∠ABD=∠ABC=70°.
∴∠CBF=180°-∠ABD-∠ABC=180°-70°-70°=40°.
∵CF⊥DB交DB的延长线于点F,
∴∠F=90°.
∴∠BCF=90°-∠CBF=90°-40°=50°.
∴∠BCF的度数是50°.
(2)∵DE=CF=4,EF=2DE,
∴BD=4+BE,EF=8.
∴BF=8-BE.
由折叠,得BD=BC=4+BE,
∵CF2+BF2=BC2,
∴42+(8-BE)2=(4+BE)2.
解得BE=,
∴BE的长是.
25.(1)证明:∵AB⊥BC,AE⊥ED,BC=9,AB=12,AE=15,ED=CD=8,
∴∠B=∠E=90°.
∴AC==15,AD==17.
∵AC2+CD2=152+82=289,AD2=172=289,
∴AC2+CD2=AD2.
∴∠ACD=90°.
∴△ACD是直角三角形.
(2)解:×12×9+×15×8+×15×8=174,
∴五边形ABCDE的面积是174.
26.解:(1)11,60,61
(2)和
证明如下:
∵n2+=n2+=
,
,
∴n2+.
由题意知,n,,三个数均为正整数,
∴n,,三个数是一组勾股数.
27.解:(1)∵∠ABC=90°,AC=25,BC=15,
∴AB==20.
∵∠PAC=∠PCA,
∴AP=PC.
设AP=PC=x,
则PB=20-x.
在Rt△PBC中,由勾股定理,得PB2+BC2=PC2,∴(20-x)2+152=x2,
解得x=,∴AP=.
(2)当CM=BC=15时,△MBC为等腰三角形,
∴AM=AC-CM=10;
当BM=BC=15时,△MBC为等腰三角形,
如图,过点B作BH⊥AC于点H,
则BH==12.
∴CH==9.
∴AM=AC-2CH=7;
当BM=CM时,△MBC为等腰三角形,
连结BM,
设AM=x,则BM=CM=25-x,
∴(25-x)2=122+(25-x-9)2.
解得x=12.5.
∴AM=12.5.
综上所述,AM的长为10或7或12.5.
