陕西省咸阳市秦都区部分学校2025年九年级下学期中考第四次模考数学试卷(含答案)
文档属性
| 名称 | 陕西省咸阳市秦都区部分学校2025年九年级下学期中考第四次模考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 18:07:30 | ||
图片预览

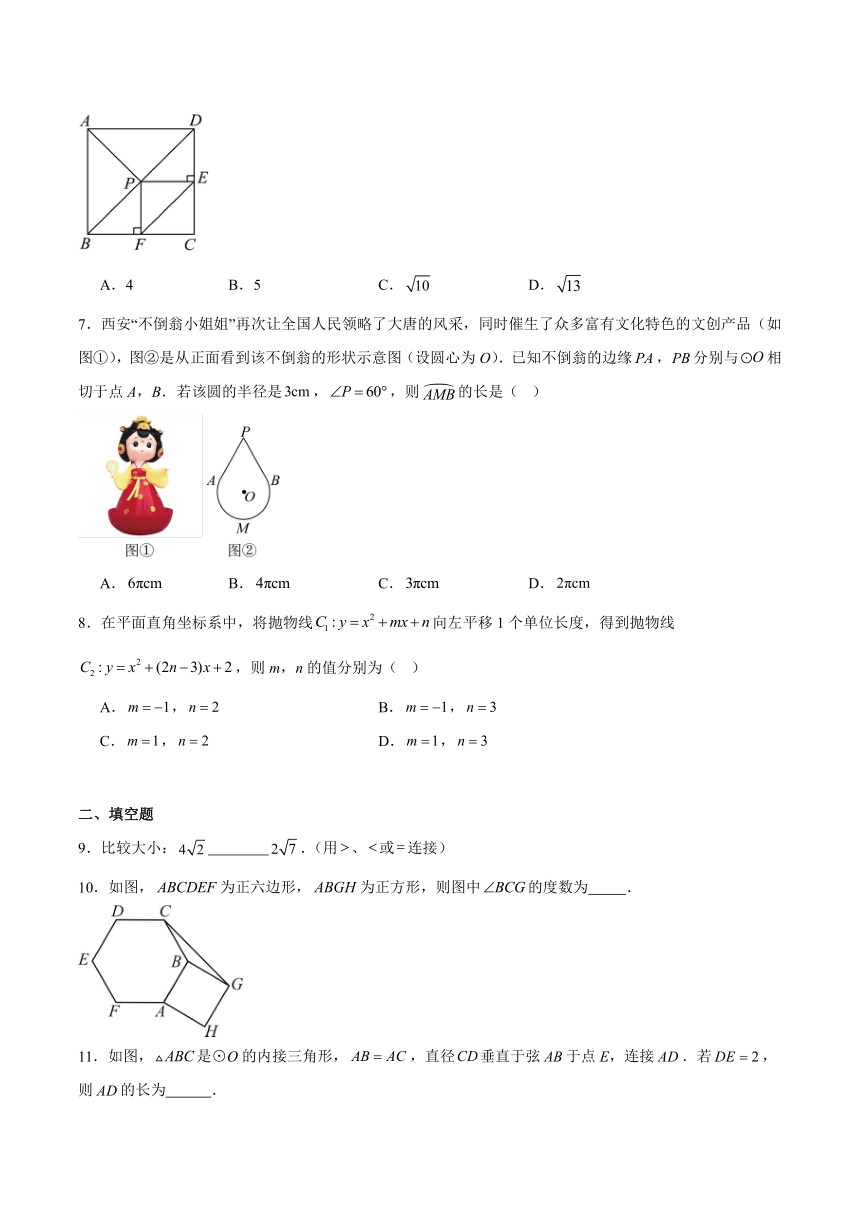


文档简介
2025年陕西省咸阳市秦都区部分学校九年级中考第四次模拟考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若零上记为“”,则零下可记为( )
A. B. C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.如图,,平分,则( )
A. B. C. D.
4.计算:( )
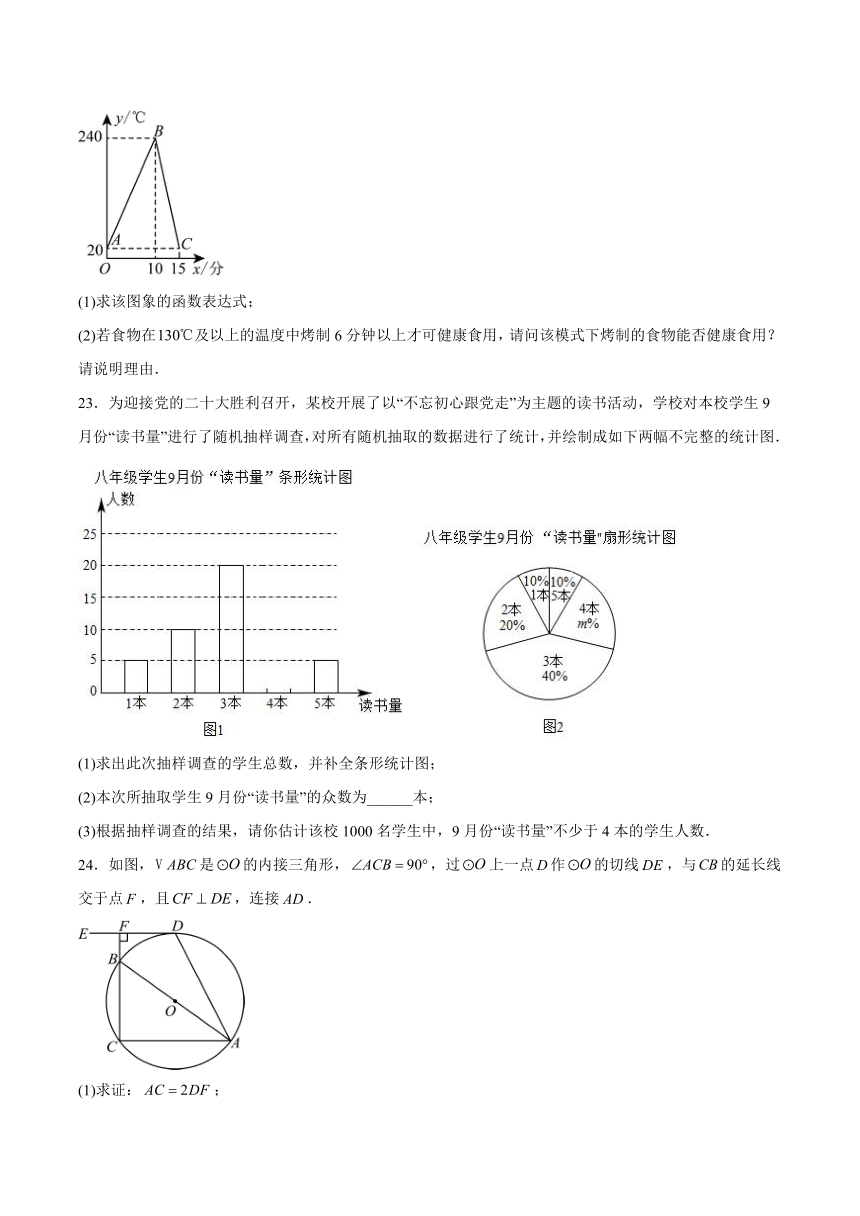
A. B. C. D.
5.若一次函数的y值随x值的增大而减小,则该函数图象经过的点的坐标可以是( )
A. B. C. D.
6.如图,已知P是正方形的对角线上一点,,,垂足分别是E,F,,,则的长为( )
A.4 B.5 C. D.
7.西安“不倒翁小姐姐”再次让全国人民领略了大唐的风采,同时催生了众多富有文化特色的文创产品(如图①),图②是从正面看到该不倒翁的形状示意图(设圆心为O).已知不倒翁的边缘,分别与相切于点A,B.若该圆的半径是,,则的长是( )
A. B. C. D.
8.在平面直角坐标系中,将抛物线向左平移1个单位长度,得到抛物线,则m,n的值分别为( )
A., B.,
C., D.,
二、填空题
9.比较大小: .(用、或连接)
10.如图,为正六边形,为正方形,则图中的度数为 .
11.如图,是⊙O的内接三角形,,直径垂直于弦于点E,连接.若,则的长为 .
12.如图,点B是反比例函数图象上的点,点A是反比例函数图象上的点,线段轴于点.若,对于反比例函数,当时,的值为 .
13.如图,在正方形中,,E,F分别为,边上的点,且,连接,交于点G,则四边形的面积为 .
三、解答题
14.计算:.
15.化简:.
16.解不等式组:
17.如图,已知等边,D为边上一点,请用尺规作图法,在线段上找一点E,使得.(保留作图痕迹,不写作法).
18.如图,点E,B在AD上,,,.求证:.
19.历史文化名城西安有着丰富的旅游资源小明计划假期来西安游玩,他打算从4个人文景点(A.大唐不夜城;B.秦始皇兵马俑;C.钟楼; D.大雁塔)中随机选取1个,再从3个自然景点(E.兴庆公园;F.秦岭野生动物园;G.中国唐苑)中随机选取1个.
(1)小明从人文景点中选中大唐不夜城的概率是_________;
(2)请利用画树状图或列表的方法,求小明恰好选中钟楼和秦岭野生动物园的概率.
20.随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.求A、B两种型号的汽车每辆进价分别为多少万元
21.为了保障市民出行方便,某市在流经该市的河流上架起一座桥,小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在、的延长线上取点D、E,使得.经测量,米,米,且点E到河岸的距离为75米.已知于点F,请你根据提供的数据 帮助他们计算桥的长度.
22.某品牌烤箱新增一种安全烤制模式,即在烤箱内温度匀速升至时烤箱停止加热,随后烤箱内温度下降至初始温度.如图所示的是该品牌烤箱安全烤制模式下烤箱内温度随时间x(分钟)变化的函数图象.
(1)求该图象的函数表达式;
(2)若食物在及以上的温度中烤制6分钟以上才可健康食用,请问该模式下烤制的食物能否健康食用?请说明理由.
23.为迎接党的二十大胜利召开,某校开展了以“不忘初心跟党走”为主题的读书活动,学校对本校学生9月份“读书量”进行了随机抽样调查,对所有随机抽取的数据进行了统计,并绘制成如下两幅不完整的统计图.
(1)求出此次抽样调查的学生总数,并补全条形统计图;
(2)本次所抽取学生9月份“读书量”的众数为______本;
(3)根据抽样调查的结果,请你估计该校1000名学生中,9月份“读书量”不少于4本的学生人数.
24.如图,是的内接三角形,,过上一点作的切线,与的延长线交于点,且,连接.
(1)求证:;
(2)若的半径为5,,求的长.
25.某农户用喷枪给斜坡上的绿地喷灌,喷出水柱的形状是一条抛物线.经测量,P处的喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点与水平线的距离为,建立如图所示的直角坐标系,水柱距喷水头的水平距离为,水柱距水平线的高度是
(1)求y与x之间的函数表达式;
(2)若斜坡的坡比为,斜坡上有一棵高的树,它与喷水头的水平距离为,请判断从P处喷出的水柱能否越过这棵树的树顶,并说明理由.
26.问题提出
(1)如图①,在矩形中,,.在边上是否存在一点M,使得的值最大?若存在,请找出点M,并求出的最大值;若不存在,请说明理由.
问题解决
(2)如图②,一支队伍沿着射线方向行进,一名观察员从点O出发,沿着射线行进,从而观察整支队伍的行进情况.已知与的夹角为,观察员行进后到达点P,观察队伍的行进情况,设其有效观测角为.若射线上存在唯一观测点P,满足,请结合题目条件求出队伍AB的长度.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B C B A D D B A
1.B
【详解】解:∵零上记为“”,
∴零下可记为.
故选:B.
2.C
【详解】解:A、是轴对称图形,但不是中心对称图形,本选项不符合题意;
B、是中心对称图形,但不是轴对称图形,本选项不符合题意;
C、既是轴对称图形又是中心对称图形,本选项符合题意;
D、是中心对称图形,但不是轴对称图形,本选项不符合题意;
故选:C.
3.B
【详解】解:∵,
∴,
∵平分,
∴,
∵,
∴,
故选:B.
4.A
【详解】解:.
故选:A.
5.D
【详解】解:一次函数的值随值的增大而减小,
.
A.当一次函数的图象过点时,,
解得:,不符合题意;
B.当一次函数的图象过点时,,不符合题意;
C.当一次函数的图象过点时,,
解得:,不符合题意;
D.当一次函数的图象过点时,,
解得:,符合题意.
故选:D.
6.D
【详解】解:如图,连接,
四边形是正方形,
,,,
在和中,
,
,
,
,,,
四边形是矩形,
,
,
,
故选:D.
7.B
【详解】解:如图,连接,,
,分别与相切于点 A, B,
,
,
,
所对圆心角为,
该圆半径是,
的长是,
故选:B.
8.A
【详解】解:,
将抛物线向左平移1个单位长度,得到抛物线的解析式为,
得到抛物线,
,
解得,
故选:A.
9.
【详解】解:,,且,
,即,
故答案为:.
10./15度
【详解】解:∵为正六边形,为正方形,
∴,,
∴,,
∴,
故答案为:.
11.
【详解】解:连接,如图所示:
∵直径垂直于弦,
∴,
∵,
∴,
∴;
∵,
∴,
∴是等边三角形;
∵,
∴;
故答案为:.
12.
【详解】解:设,点的横坐标为,
∴,
解得,
∴,
∴,
解得,
∴,
当时,的值为,
故答案为:.
13.
【详解】解:四边形是正方形,
∴,,
∴
∵,
,
∴,
∴,,
∴,
∴,
∵,
∴,
则,
∴,
则,
∴,
则四边形的面积梯形的面积
.
故答案为:.
14.
【详解】解:
.
15.
【详解】解:
16.
【详解】解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为.
17.见解析
【详解】解:以点D为角的顶点,角的一条边,作,交于一点E,则为所求作的三角形,如图所示:
∵为等边三角形,
∴,
∵,
∴.
18.见解析
【详解】证明:∵,
∴,
∵,
∴,
即,
又∵,
∴,
∴,
∴.
19.(1)
(2)
【详解】(1)解:选中大唐不夜城的概率是,
故答案为:;
(2)解:树状图如下:
∵等可能出现的结果为种,符合条件的只有一种,
∴小明恰好选中钟楼和秦岭野生动物园的概率为.
20.A、B两种型号的汽车每辆进价分别为25万元、10万元
【详解】解:设A种型号的汽车每辆进价为x万元,B种型号的汽车每辆进价为y万元,
由题意可得,,
解得,
答:A、B两种型号的汽车每辆进价分别为25万元、10万元;
21.100米
【详解】解:如图所示,过作于,
,
,
,
,
,,
,
,
,
,
,即,
解得:,
桥的长度为100米.
22.(1)
(2)该模式下烤制的食物可以健康食用.
【详解】(1)设段的函数表达式为,
将点和点代入函数表达式,
得,
解得,
段的函数表达式为.
设段的函数表达式为,
将点和点代入函数表达式,
,
解得得.
段的函数表达式为.
∴该图象的函数表达式;
(2)令,即,
解得,
令,即,
解得,(分钟).
,
该模式下烤制的食物可以健康食用.
23.(1)50名,图形见解析
(2)3
(3)300名
【详解】(1)解:此次抽样调查的学生总数为名,
“读书量”为4本的人数为名,
补全条形统计图,如下:
(2)解:根据题意得:“读书量”为3本的人数最多,
∴本次所抽取学生9月份“读书量”的众数为3本;
故答案为:3
(3)解:名,
答:9月份“读书量”不少于4本的学生人数为300名.
24.(1)见详解
(2)2
【详解】(1)证明:如图,连接,并延长交于点,
∵与相切,
∴,
∵,
∴,
又∵,
∴四边形是矩形,
∴,,
由垂径定理得,,
∴;
(2)解:如图,连接,
,
∴,
∴,即,
∴,
假设,则,
由(1)可知,,
∴,
∵的半径为5,
∴,,
由勾股定理得,,
即,
解得或(不符合题意,舍去),
∴的长为2.
25.(1)抛物线解析式为;
(2)不能,理由见解析.
【详解】(1)解:设与之间的函数表达式为,
由题可知,其图象顶点坐标为,
抛物线解析式为.
又抛物线过点,
.
.
抛物线解析式为.
(2)解:不能,理由如下:
如图,过点作于,
由题意得点的横坐标为5,即,斜坡的坡比为,
,
,
,
,
当时,,
,
处喷出的水柱不能越过这棵树的树顶.
26.(1)存在,(2)米
【详解】解:(1)存在,理由如下:
如图,作的外接圆,根据题意,当与相切时,满足题意.连接并延长与交于点,连接,由与相切,可知,故在矩形中,,
,
,,
,
又,即,
设的半径为,
在中,,
即,解得,
;
(2)如图,作的外接圆,根据题意可知当与相切于点时,满足题意,连接并延长与交于点,连接,过点作,垂足为,
,,
,
,
,
,
又,
,
由与相切可知,即,
在中,,故,
设的半径为,
在中,,
在中,,
而,
解得,
,
即队伍的长度为米.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若零上记为“”,则零下可记为( )
A. B. C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.如图,,平分,则( )
A. B. C. D.
4.计算:( )
A. B. C. D.
5.若一次函数的y值随x值的增大而减小,则该函数图象经过的点的坐标可以是( )
A. B. C. D.
6.如图,已知P是正方形的对角线上一点,,,垂足分别是E,F,,,则的长为( )
A.4 B.5 C. D.
7.西安“不倒翁小姐姐”再次让全国人民领略了大唐的风采,同时催生了众多富有文化特色的文创产品(如图①),图②是从正面看到该不倒翁的形状示意图(设圆心为O).已知不倒翁的边缘,分别与相切于点A,B.若该圆的半径是,,则的长是( )
A. B. C. D.
8.在平面直角坐标系中,将抛物线向左平移1个单位长度,得到抛物线,则m,n的值分别为( )
A., B.,
C., D.,
二、填空题
9.比较大小: .(用、或连接)
10.如图,为正六边形,为正方形,则图中的度数为 .
11.如图,是⊙O的内接三角形,,直径垂直于弦于点E,连接.若,则的长为 .
12.如图,点B是反比例函数图象上的点,点A是反比例函数图象上的点,线段轴于点.若,对于反比例函数,当时,的值为 .
13.如图,在正方形中,,E,F分别为,边上的点,且,连接,交于点G,则四边形的面积为 .
三、解答题
14.计算:.
15.化简:.
16.解不等式组:
17.如图,已知等边,D为边上一点,请用尺规作图法,在线段上找一点E,使得.(保留作图痕迹,不写作法).
18.如图,点E,B在AD上,,,.求证:.
19.历史文化名城西安有着丰富的旅游资源小明计划假期来西安游玩,他打算从4个人文景点(A.大唐不夜城;B.秦始皇兵马俑;C.钟楼; D.大雁塔)中随机选取1个,再从3个自然景点(E.兴庆公园;F.秦岭野生动物园;G.中国唐苑)中随机选取1个.
(1)小明从人文景点中选中大唐不夜城的概率是_________;
(2)请利用画树状图或列表的方法,求小明恰好选中钟楼和秦岭野生动物园的概率.
20.随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.求A、B两种型号的汽车每辆进价分别为多少万元
21.为了保障市民出行方便,某市在流经该市的河流上架起一座桥,小明和小颖想通过自己所学的数学知识计算该桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在、的延长线上取点D、E,使得.经测量,米,米,且点E到河岸的距离为75米.已知于点F,请你根据提供的数据 帮助他们计算桥的长度.
22.某品牌烤箱新增一种安全烤制模式,即在烤箱内温度匀速升至时烤箱停止加热,随后烤箱内温度下降至初始温度.如图所示的是该品牌烤箱安全烤制模式下烤箱内温度随时间x(分钟)变化的函数图象.
(1)求该图象的函数表达式;
(2)若食物在及以上的温度中烤制6分钟以上才可健康食用,请问该模式下烤制的食物能否健康食用?请说明理由.
23.为迎接党的二十大胜利召开,某校开展了以“不忘初心跟党走”为主题的读书活动,学校对本校学生9月份“读书量”进行了随机抽样调查,对所有随机抽取的数据进行了统计,并绘制成如下两幅不完整的统计图.
(1)求出此次抽样调查的学生总数,并补全条形统计图;
(2)本次所抽取学生9月份“读书量”的众数为______本;
(3)根据抽样调查的结果,请你估计该校1000名学生中,9月份“读书量”不少于4本的学生人数.
24.如图,是的内接三角形,,过上一点作的切线,与的延长线交于点,且,连接.
(1)求证:;
(2)若的半径为5,,求的长.
25.某农户用喷枪给斜坡上的绿地喷灌,喷出水柱的形状是一条抛物线.经测量,P处的喷水头距地面,水柱在距喷水头水平距离处达到最高,最高点与水平线的距离为,建立如图所示的直角坐标系,水柱距喷水头的水平距离为,水柱距水平线的高度是
(1)求y与x之间的函数表达式;
(2)若斜坡的坡比为,斜坡上有一棵高的树,它与喷水头的水平距离为,请判断从P处喷出的水柱能否越过这棵树的树顶,并说明理由.
26.问题提出
(1)如图①,在矩形中,,.在边上是否存在一点M,使得的值最大?若存在,请找出点M,并求出的最大值;若不存在,请说明理由.
问题解决
(2)如图②,一支队伍沿着射线方向行进,一名观察员从点O出发,沿着射线行进,从而观察整支队伍的行进情况.已知与的夹角为,观察员行进后到达点P,观察队伍的行进情况,设其有效观测角为.若射线上存在唯一观测点P,满足,请结合题目条件求出队伍AB的长度.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B C B A D D B A
1.B
【详解】解:∵零上记为“”,
∴零下可记为.
故选:B.
2.C
【详解】解:A、是轴对称图形,但不是中心对称图形,本选项不符合题意;
B、是中心对称图形,但不是轴对称图形,本选项不符合题意;
C、既是轴对称图形又是中心对称图形,本选项符合题意;
D、是中心对称图形,但不是轴对称图形,本选项不符合题意;
故选:C.
3.B
【详解】解:∵,
∴,
∵平分,
∴,
∵,
∴,
故选:B.
4.A
【详解】解:.
故选:A.
5.D
【详解】解:一次函数的值随值的增大而减小,
.
A.当一次函数的图象过点时,,
解得:,不符合题意;
B.当一次函数的图象过点时,,不符合题意;
C.当一次函数的图象过点时,,
解得:,不符合题意;
D.当一次函数的图象过点时,,
解得:,符合题意.
故选:D.
6.D
【详解】解:如图,连接,
四边形是正方形,
,,,
在和中,
,
,
,
,,,
四边形是矩形,
,
,
,
故选:D.
7.B
【详解】解:如图,连接,,
,分别与相切于点 A, B,
,
,
,
所对圆心角为,
该圆半径是,
的长是,
故选:B.
8.A
【详解】解:,
将抛物线向左平移1个单位长度,得到抛物线的解析式为,
得到抛物线,
,
解得,
故选:A.
9.
【详解】解:,,且,
,即,
故答案为:.
10./15度
【详解】解:∵为正六边形,为正方形,
∴,,
∴,,
∴,
故答案为:.
11.
【详解】解:连接,如图所示:
∵直径垂直于弦,
∴,
∵,
∴,
∴;
∵,
∴,
∴是等边三角形;
∵,
∴;
故答案为:.
12.
【详解】解:设,点的横坐标为,
∴,
解得,
∴,
∴,
解得,
∴,
当时,的值为,
故答案为:.
13.
【详解】解:四边形是正方形,
∴,,
∴
∵,
,
∴,
∴,,
∴,
∴,
∵,
∴,
则,
∴,
则,
∴,
则四边形的面积梯形的面积
.
故答案为:.
14.
【详解】解:
.
15.
【详解】解:
16.
【详解】解:
解不等式①得:,
解不等式②得:,
∴不等式组的解集为.
17.见解析
【详解】解:以点D为角的顶点,角的一条边,作,交于一点E,则为所求作的三角形,如图所示:
∵为等边三角形,
∴,
∵,
∴.
18.见解析
【详解】证明:∵,
∴,
∵,
∴,
即,
又∵,
∴,
∴,
∴.
19.(1)
(2)
【详解】(1)解:选中大唐不夜城的概率是,
故答案为:;
(2)解:树状图如下:
∵等可能出现的结果为种,符合条件的只有一种,
∴小明恰好选中钟楼和秦岭野生动物园的概率为.
20.A、B两种型号的汽车每辆进价分别为25万元、10万元
【详解】解:设A种型号的汽车每辆进价为x万元,B种型号的汽车每辆进价为y万元,
由题意可得,,
解得,
答:A、B两种型号的汽车每辆进价分别为25万元、10万元;
21.100米
【详解】解:如图所示,过作于,
,
,
,
,
,,
,
,
,
,
,即,
解得:,
桥的长度为100米.
22.(1)
(2)该模式下烤制的食物可以健康食用.
【详解】(1)设段的函数表达式为,
将点和点代入函数表达式,
得,
解得,
段的函数表达式为.
设段的函数表达式为,
将点和点代入函数表达式,
,
解得得.
段的函数表达式为.
∴该图象的函数表达式;
(2)令,即,
解得,
令,即,
解得,(分钟).
,
该模式下烤制的食物可以健康食用.
23.(1)50名,图形见解析
(2)3
(3)300名
【详解】(1)解:此次抽样调查的学生总数为名,
“读书量”为4本的人数为名,
补全条形统计图,如下:
(2)解:根据题意得:“读书量”为3本的人数最多,
∴本次所抽取学生9月份“读书量”的众数为3本;
故答案为:3
(3)解:名,
答:9月份“读书量”不少于4本的学生人数为300名.
24.(1)见详解
(2)2
【详解】(1)证明:如图,连接,并延长交于点,
∵与相切,
∴,
∵,
∴,
又∵,
∴四边形是矩形,
∴,,
由垂径定理得,,
∴;
(2)解:如图,连接,
,
∴,
∴,即,
∴,
假设,则,
由(1)可知,,
∴,
∵的半径为5,
∴,,
由勾股定理得,,
即,
解得或(不符合题意,舍去),
∴的长为2.
25.(1)抛物线解析式为;
(2)不能,理由见解析.
【详解】(1)解:设与之间的函数表达式为,
由题可知,其图象顶点坐标为,
抛物线解析式为.
又抛物线过点,
.
.
抛物线解析式为.
(2)解:不能,理由如下:
如图,过点作于,
由题意得点的横坐标为5,即,斜坡的坡比为,
,
,
,
,
当时,,
,
处喷出的水柱不能越过这棵树的树顶.
26.(1)存在,(2)米
【详解】解:(1)存在,理由如下:
如图,作的外接圆,根据题意,当与相切时,满足题意.连接并延长与交于点,连接,由与相切,可知,故在矩形中,,
,
,,
,
又,即,
设的半径为,
在中,,
即,解得,
;
(2)如图,作的外接圆,根据题意可知当与相切于点时,满足题意,连接并延长与交于点,连接,过点作,垂足为,
,,
,
,
,
,
又,
,
由与相切可知,即,
在中,,故,
设的半径为,
在中,,
在中,,
而,
解得,
,
即队伍的长度为米.
同课章节目录
