2025-2026学年人教版九年级数学上册 21.2 第2课时 配方法 课件(26张ppt)
文档属性
| 名称 | 2025-2026学年人教版九年级数学上册 21.2 第2课时 配方法 课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 571.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 00:00:00 | ||
图片预览







文档简介
第2课时 配方法
第二十一章 一元二次方程
情 境 导 入
第2课时 配方法
a2+2ab+b2=_________;
a2-2ab+b2=_________.
完全平方公式:
(a-b)2
填上适当的数或式,使下列各等式成立.
(1)x2+6x+___=(x+3)2
(2)x2+8x+___=(x+4)2
(3)x2-4x+___=(x____)2
32
42
22
-2
(a+b)2
复习回顾
新 课 探 究
第2课时 配方法
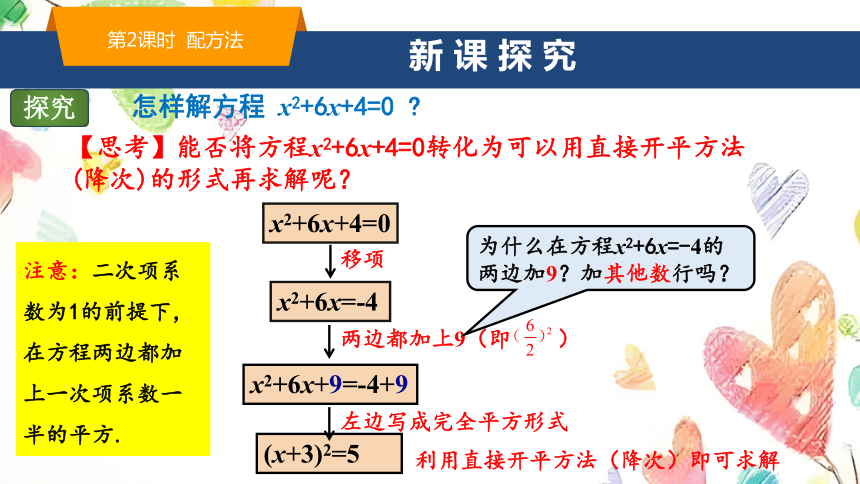
怎样解方程 x2+6x+4=0 ?
【思考】能否将方程x2+6x+4=0转化为可以用直接开平方法(降次)的形式再求解呢?
x2+6x+4=0
x2+6x=-4
移项
x2+6x+9=-4+9
两边都加上9(即 )
(x+3)2=5
为什么在方程x2+6x=-4的两边加9?加其他数行吗?
左边写成完全平方形式
利用直接开平方法(降次)即可求解
探究
注意:二次项系数为1的前提下,在方程两边都加上一次项系数一半的平方.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
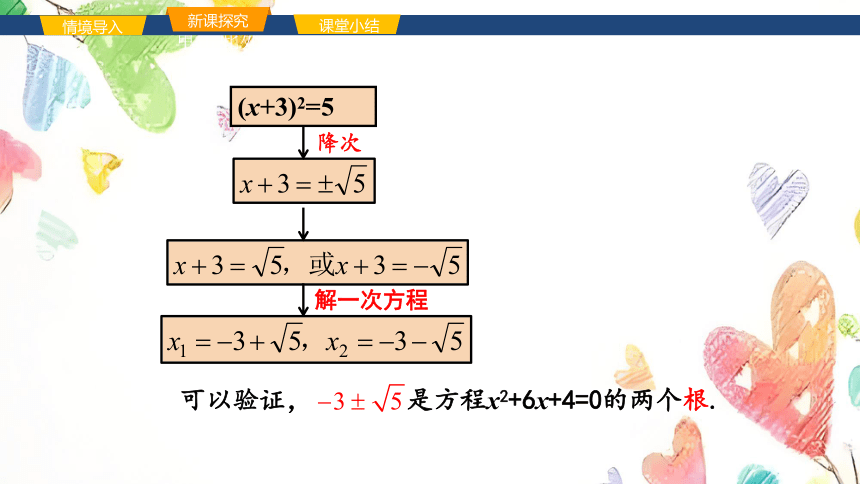
可以验证, 是方程x2+6x+4=0的两个根.
(x+3)2=5
降次
解一次方程
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
像上面这样通过配成完全平方式来解一元二次方程,叫作配方法.
配方法的定义
配方法解方程的基本思路
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为一元一次方程求解.
归纳
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1 解下列一元二次方程:
(1)x2-8x+1=0 (2)2x2+1=3x (3)3x2-6x+4=0
典例精析
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(2)移项,得:
系数化为1,得:
2x2﹣3x=﹣1
配方,得:
由此可得:
解:(1)移项,得:
配方,得:
x2﹣8x=﹣1
x2﹣8x+42=﹣1+42
(x﹣4)2=15
整理,得:
由此可得:
±????????
?
∴ x1=4+ ???????? ,x2=4- ????????.
?
x﹣4=
(1)x2-8x+1=0 (2)2x2+1=3x
即
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:移项,得:
系数化为1,得:
配方,得:
整理,得:
(3)3x2-6x+4=0
因为实数的平方不会是负数,所以x取任何实数时,(x﹣1)2都是非负数,上式都不成立,即原方程无实数根.
新课探究
情境导入
课堂小结
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
思考1:用配方法解一元二次方程时,移项时要注意些什么?
思考2:用配方法解一元二次方程的一般步骤.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为 x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p.
总结归纳
新课探究
情境导入
课堂小结
1.填空
(1)x2+4x+ =(x+ )2
(2)x2-8x+ =(x- )2
(3)x2+x+ =(x+ )2
练习
4 2
16 4
新课探究
情境导入
课堂小结
2.用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A.x2+4x=5 B.2x2-4x=5
C.x2-2x=5 D.x2+2x=5
3.用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A.(x+4)2=-9 B.(x+4)2=-7
C.(x+4)2=25 D.(x+4)2=7
A
D
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.解下列方程:
(1)x2+10x+9=0 (2)x2+4x-9=2x-11
(x+5)2=16
解(1)x2+10x=-9
x2+10x+52=-9+52
x+5=±4
x1=-1,x2=-9
(2)x2+2x+2=0
x2+2x=-2
x2+2x+12=-2+12
(x+1)2=-1
因为(x+1)2 ≥0,而–1<0,即方程无实数根.
课 堂 小 结
第2课时 配方法
通过本节课的学习
1.你掌握了哪些知识?
2.你学会了哪些解题方法?
3.你运用了哪些数学思想?
4.你总结了哪些学习经验?
5.还有什么感悟和思考?
情境导入
课堂小结
新课探究
定义
通过配成完全平方形式解一元二次方程的方法.
步骤
一移常数项;
二配方[配上(一次项系数????)2 ];
三写成(x+n)2=p(p ≥0);
四直接开平方法解方程.
?
应用
求代数式的最值或证明
配方法
注意:在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
1.(人教9上P9改编、北师9上P36改编)填空:
(1)x2-2x+1=(x- )2;?
(2)x2+6x+ =(x+ )2;?
(3)x2-x+ =(x- )2.?
?
?
3
9
1
14
?
12
?
课后练习
2.用配方法解方程:
(1)(2023无锡)x2-2x-4=0;
x=1±5
?
(2)(人教9上P6)x2+6x+4=0;
x=-3±5
?
(3)x2-x-1=0.
x=1±52
?
小结:配方法的关键是化成(mx+n)2=p的形式.
3.(2024深圳模拟)用配方法解方程x2+2x=3时,配方后正确的是( )
A.(x+2)2=7 B.(x+2)2=5
C.(x+1)2=4 D.(x+1)2=2
C
4.(2024新疆)用配方法解一元二次方程x2-6x+8=0,配方后得到的方程是( )
A.(x+6)2=28 B.(x-6)2=28
C.(x+3)2=1 D.(x-3)2=1
D
5.【例3】(人教9上P9、北师9上P37改编)用配方法解一元二次方程:
(1)x2+10x+9=0; (2)x(x+8)=16.
解:(1)x2+10x+25=-9+25,
所以(x+5)2=16,
x+5=±4,所以x1=-1,x2=-9.
(2)x2+8x=16,x2+8x+16=16+16,
所以(x+4)2=32,x+4=±4 2,
所以x1=4 2-4,x2=-4 2-4.
?
6.【例4】(人教9上P9改编、北师9上P38)用配方法解一元二次方程:
(1)2x2+4x-10=0; (2)3x2+8x-3=0.
解:(1)x2+2x-5=0,x2+2x+1=5+1,
所以(x+1)2=6,x+1=±6,
所以x1=6-1,x2=-6-1.
(2)x2+83x=1,x2+83x+169=1+169,
所以x+432=259,x+43=±53,
所以x1=13,x2=-3.
?
8.将一元二次方程x2-10x+10=0化成(x-a)2=b的形式,则ab= .
75
9.用配方法解一元二次方程:
(1)x2-2x-2=0; (2)(x-1)(x-2)=8.
(1)x1=1+3,x2=1-3
(2)x1=3+332,x2=3-332
?
10.(人教9上P9、北师9上P39改编)用配方法解一元二次方程:
(1)3x2+6x-4=0; (2)4x2-6x-3=0.
(1)x1=-1+213,x2=-1-213
(2)x1=3+214,x2=3-214
?
★11. 0.45 已知a,b,c满足a2-2c=-17,
b2-6a=-1,c2+2b=7,则a+b+c= .?
3
THANK YOU
第二十一章 一元二次方程
情 境 导 入
第2课时 配方法
a2+2ab+b2=_________;
a2-2ab+b2=_________.
完全平方公式:
(a-b)2
填上适当的数或式,使下列各等式成立.
(1)x2+6x+___=(x+3)2
(2)x2+8x+___=(x+4)2
(3)x2-4x+___=(x____)2
32
42
22
-2
(a+b)2
复习回顾
新 课 探 究
第2课时 配方法
怎样解方程 x2+6x+4=0 ?
【思考】能否将方程x2+6x+4=0转化为可以用直接开平方法(降次)的形式再求解呢?
x2+6x+4=0
x2+6x=-4
移项
x2+6x+9=-4+9
两边都加上9(即 )
(x+3)2=5
为什么在方程x2+6x=-4的两边加9?加其他数行吗?
左边写成完全平方形式
利用直接开平方法(降次)即可求解
探究
注意:二次项系数为1的前提下,在方程两边都加上一次项系数一半的平方.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
可以验证, 是方程x2+6x+4=0的两个根.
(x+3)2=5
降次
解一次方程
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
像上面这样通过配成完全平方式来解一元二次方程,叫作配方法.
配方法的定义
配方法解方程的基本思路
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为一元一次方程求解.
归纳
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
例1 解下列一元二次方程:
(1)x2-8x+1=0 (2)2x2+1=3x (3)3x2-6x+4=0
典例精析
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
(2)移项,得:
系数化为1,得:
2x2﹣3x=﹣1
配方,得:
由此可得:
解:(1)移项,得:
配方,得:
x2﹣8x=﹣1
x2﹣8x+42=﹣1+42
(x﹣4)2=15
整理,得:
由此可得:
±????????
?
∴ x1=4+ ???????? ,x2=4- ????????.
?
x﹣4=
(1)x2-8x+1=0 (2)2x2+1=3x
即
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
解:移项,得:
系数化为1,得:
配方,得:
整理,得:
(3)3x2-6x+4=0
因为实数的平方不会是负数,所以x取任何实数时,(x﹣1)2都是非负数,上式都不成立,即原方程无实数根.
新课探究
情境导入
课堂小结
移项时需注意改变符号.
①移项,二次项系数化为1;
②左边配成完全平方式;
③左边写成完全平方形式;
④降次;
⑤解一次方程.
思考1:用配方法解一元二次方程时,移项时要注意些什么?
思考2:用配方法解一元二次方程的一般步骤.
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
①当p>0时,则 ,方程的两个根为
②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为 x1=x2=-n.
③当p<0时,则方程(x+n)2=p无实数根.
一般地,如果一个一元二次方程通过配方转化成(x+n)2=p.
总结归纳
新课探究
情境导入
课堂小结
1.填空
(1)x2+4x+ =(x+ )2
(2)x2-8x+ =(x- )2
(3)x2+x+ =(x+ )2
练习
4 2
16 4
新课探究
情境导入
课堂小结
2.用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A.x2+4x=5 B.2x2-4x=5
C.x2-2x=5 D.x2+2x=5
3.用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
A.(x+4)2=-9 B.(x+4)2=-7
C.(x+4)2=25 D.(x+4)2=7
A
D
单击此处添加标题文本内容
新课探究
情境导入
课堂小结
4.解下列方程:
(1)x2+10x+9=0 (2)x2+4x-9=2x-11
(x+5)2=16
解(1)x2+10x=-9
x2+10x+52=-9+52
x+5=±4
x1=-1,x2=-9
(2)x2+2x+2=0
x2+2x=-2
x2+2x+12=-2+12
(x+1)2=-1
因为(x+1)2 ≥0,而–1<0,即方程无实数根.
课 堂 小 结
第2课时 配方法
通过本节课的学习
1.你掌握了哪些知识?
2.你学会了哪些解题方法?
3.你运用了哪些数学思想?
4.你总结了哪些学习经验?
5.还有什么感悟和思考?
情境导入
课堂小结
新课探究
定义
通过配成完全平方形式解一元二次方程的方法.
步骤
一移常数项;
二配方[配上(一次项系数????)2 ];
三写成(x+n)2=p(p ≥0);
四直接开平方法解方程.
?
应用
求代数式的最值或证明
配方法
注意:在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
1.(人教9上P9改编、北师9上P36改编)填空:
(1)x2-2x+1=(x- )2;?
(2)x2+6x+ =(x+ )2;?
(3)x2-x+ =(x- )2.?
?
?
3
9
1
14
?
12
?
课后练习
2.用配方法解方程:
(1)(2023无锡)x2-2x-4=0;
x=1±5
?
(2)(人教9上P6)x2+6x+4=0;
x=-3±5
?
(3)x2-x-1=0.
x=1±52
?
小结:配方法的关键是化成(mx+n)2=p的形式.
3.(2024深圳模拟)用配方法解方程x2+2x=3时,配方后正确的是( )
A.(x+2)2=7 B.(x+2)2=5
C.(x+1)2=4 D.(x+1)2=2
C
4.(2024新疆)用配方法解一元二次方程x2-6x+8=0,配方后得到的方程是( )
A.(x+6)2=28 B.(x-6)2=28
C.(x+3)2=1 D.(x-3)2=1
D
5.【例3】(人教9上P9、北师9上P37改编)用配方法解一元二次方程:
(1)x2+10x+9=0; (2)x(x+8)=16.
解:(1)x2+10x+25=-9+25,
所以(x+5)2=16,
x+5=±4,所以x1=-1,x2=-9.
(2)x2+8x=16,x2+8x+16=16+16,
所以(x+4)2=32,x+4=±4 2,
所以x1=4 2-4,x2=-4 2-4.
?
6.【例4】(人教9上P9改编、北师9上P38)用配方法解一元二次方程:
(1)2x2+4x-10=0; (2)3x2+8x-3=0.
解:(1)x2+2x-5=0,x2+2x+1=5+1,
所以(x+1)2=6,x+1=±6,
所以x1=6-1,x2=-6-1.
(2)x2+83x=1,x2+83x+169=1+169,
所以x+432=259,x+43=±53,
所以x1=13,x2=-3.
?
8.将一元二次方程x2-10x+10=0化成(x-a)2=b的形式,则ab= .
75
9.用配方法解一元二次方程:
(1)x2-2x-2=0; (2)(x-1)(x-2)=8.
(1)x1=1+3,x2=1-3
(2)x1=3+332,x2=3-332
?
10.(人教9上P9、北师9上P39改编)用配方法解一元二次方程:
(1)3x2+6x-4=0; (2)4x2-6x-3=0.
(1)x1=-1+213,x2=-1-213
(2)x1=3+214,x2=3-214
?
★11. 0.45 已知a,b,c满足a2-2c=-17,
b2-6a=-1,c2+2b=7,则a+b+c= .?
3
THANK YOU
同课章节目录
