江苏省泰州市姜堰区2024-2025学年七年级下学期6月期末考试数学试卷(含答案)
文档属性
| 名称 | 江苏省泰州市姜堰区2024-2025学年七年级下学期6月期末考试数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览




文档简介
江苏省泰州市姜堰区2024-2025学年七年级下学期6月期末数学试题
一、单选题
1.下列计算正确的是( )
A. B.
C. D.
2.用不等式表示图中的解集,下列正确的是( )
A. B. C. D.
3.如图,和相交于点,若,用“”证明还需( )
A. B. C. D.
4.在国内投寄一封平信应付邮资如下表:
信件质量(克)
邮资(元/封)
某人投寄一封平信花费元,则此平信的质量可能为( )
A.克 B.克 C.克 D.克
5.要说明命题“若,则”是假命题,能举的一个反例是( )
A., B., C., D.,
6.如图,为的中线,将沿翻折,使点B落在点E处,与边交于点F.记的面积为,的面积为,要想求的值,只要知道( )
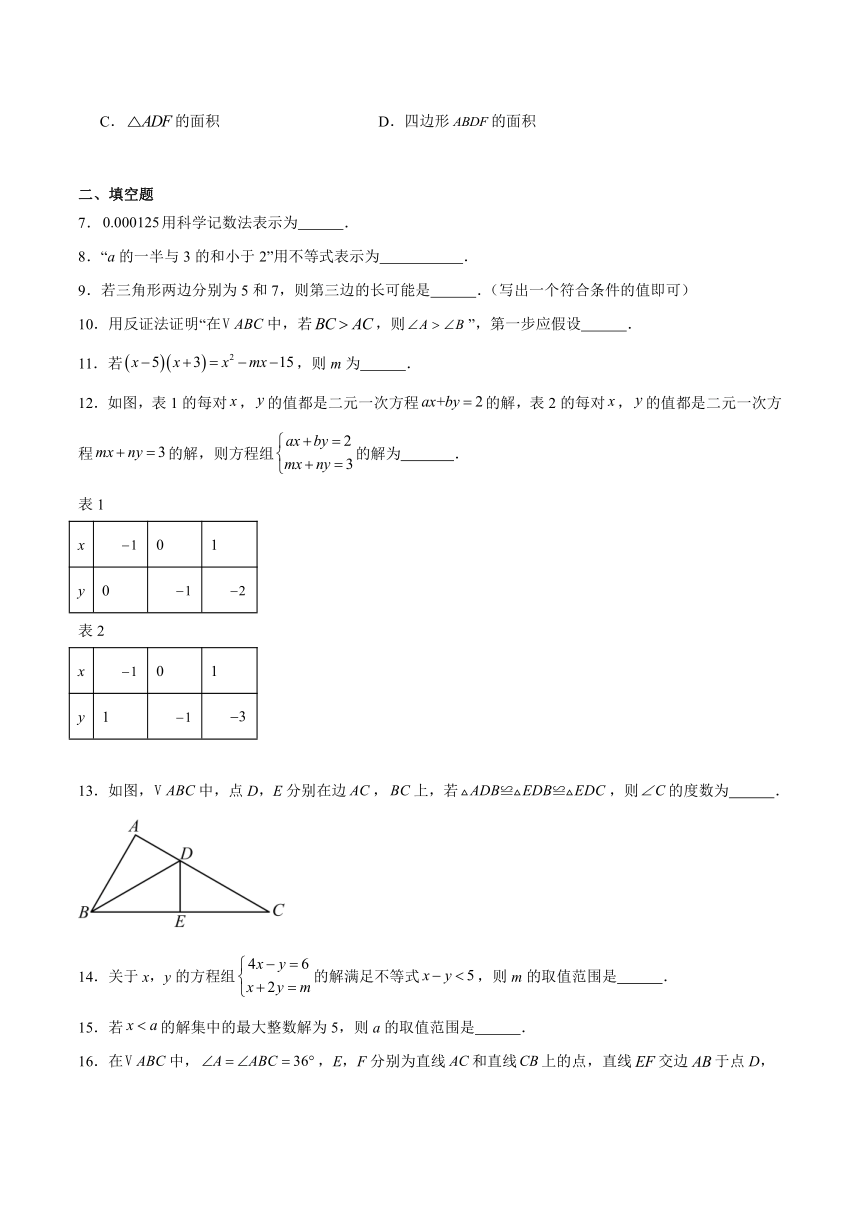
A.的面积 B.的面积
C.的面积 D.四边形的面积
二、填空题
7.用科学记数法表示为 .
8.“a的一半与3的和小于2”用不等式表示为 .
9.若三角形两边分别为5和7,则第三边的长可能是 .(写出一个符合条件的值即可)
10.用反证法证明“在中,若,则”,第一步应假设 .
11.若,则m为 .
12.如图,表1的每对,的值都是二元一次方程的解,表2的每对,的值都是二元一次方程的解,则方程组的解为 .
表1
x 0 1
y 0
表2
x 0 1
y 1
13.如图,中,点D,E分别在边,上,若,则的度数为 .
14.关于x,y的方程组的解满足不等式,则m的取值范围是 .
15.若的解集中的最大整数解为5,则a的取值范围是 .
16.在中,,E,F分别为直线和直线上的点,直线交边于点D,,,则 .
三、解答题
17.计算或化简:
(1)
(2)
18.计算或化简:
(1)
(2)
19.解方程组或不等式组
(1)解方程组:
(2)解不等式组:
20.正方形网格中的每个小正方形的边长均为个单位长度,各顶点的位置如图所示.将平移,使点移到点,点分别是的对应点.
(1)画出平移后的;
(2)在整个平移的过程中,扫过的面积是______.
21.我们把关于x、y的二元一次方程的系数a、b、c称为该方程的伴随数,记作.例如:二元一次方程的伴随数是.
(1)二元一次方程的伴随数是__________
(2)已知关于x、y的二元一次方程的伴随数是,且,是该方程的两组解,求m、n的值.
22.如图,、为两条线段,E为线段上方一点,连结交AB于F,过点E作直线交,于G,H,.
(1)求证:;
(2)若,求的度数.
23.某水果店经销甲、乙两种水果,两次购进水果的情况如表所示(两次进货时,两种水果的进价保持不变):
进货批次 甲种水果(单位:千克) 乙种水果(单位:千克) 总费用(单位:元)
第一次 80 50 2500
第二次 40 70 2420
(1)求甲、乙两种水果的进价;
(2)第一次和第二次购进的水果全部售完后,在两种水果进价不变的情况下,第三次又购进甲、乙两种水果共150千克,购买的资金不超过3240元,则第三次购进的甲种水果至少为多少千克?
24.已知代数式,,其中,为常数.
(1)若与的乘积化简后不含的一次项,求的值(用含的代数式表示);
(2)在()的条件下,是不等式的解,不是不等式的解,求整数的值.
25.如图1,在直角中,,D为上一点,E为外一点,,,.
(1)求证:;
(2)若(如图2),点F在线段上,.
①当时,求的面积;
②小亮说:可以看作由经过两次轴对称变换得到.他的说法是否正确,若正确,用圆规和没有刻度的直尺在图3中作出两条对称轴(若有多种情况,作出一种情况即可);若不正确,请写出一种正确的变换方式.
26.阅读下面材料,并按要求完成相应的任务:
如何快速判断一个较为复杂的整数能否被3整除?小明对下列一些能被3整除的整数进行了研究:27,123,159,246,1233,23454. 小明通过观察、计算发现:这些整数各个数位上的数字之和都能被3整除,如:整数246各个数位上的数字之和为,12能被3整除;整数1233各个数位上的数字之和为,9能被3整除.由此,他提出了这样一个命题; 命题1:如果一个数能被3整除,那么这个数各个数位上的数字之和能被3整除.小明以两位数为例进行了证明; 设是一个两位数,若两位数能被3整除,求证:能被3整除. 证明:∵两位数能被3整除, ∴设(k为正整数)... .为整数.可以被3整除. 由此推断,命题1是一个真命题,紧接着对它的逆命题进行了研究,发现命题1的逆命题也是真命题. 结论:在判断一个数是否能被3整除时,可以通过计算其各个数位上数字之和来进行快速判断. 小明在研究时还发现,整数123中,;整数159中,;整数246中,.于是,他又提出了这样一个命题; 命题2:如果一个三位数能被3整除,那么这个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍.
任务1:证明命题
(1)设是一个三位数,若可以被3整除,求证:这个三位数也能被3整除.
任务2:写逆命题
(2)判断命题2是真命题还是假命题,并写出它的逆命题;
任务3:应用结论
(3)若四位数能被3整除,且,这个四位数的最小值为______.
(4)小亮在匀速行驶的汽车里,注意到公路里程碑上的数是一个能被3整除的两位数;后,看到里程碑上的两位数与第一次看到的两位数恰好互换了两个数字的位置;再过,看到里程碑上的数是第一次看到的两位数的两个数字之间添加一个数字m所得的三位数,且这个三位数也能被3整除.则第一次看到的里程碑上的两位数是多少?
参考答案
1.A
解:A.,计算正确,故此选项符合题意;
B.,计算错误,故此选项不符合题意;
C.,计算错误,故此选项不符合题意;
D.,计算错误,故此选项不符合题意;
故选A.
2.B
解:由数轴可得:,
故选:B.
3.B
解:在和中,,,
若要用证明,则需要添加条件,
故选:.
4.C
解:由表格可知,当信件质量满足时,邮资为元,
∴此平信的质量可能为克,
故选:.
5.D
解:当,时,,而,
∴命题“若,则”是假命题,
故选:D.
6.C
解:∵为的中线,
∴,
由折叠的性质得:,
∴,
∵,,,
∴,
∴想求的值,只要知道的面积即可,
故选:C.
7.
解:∵,
故答案为:.
8.
解:由题意得,.
故答案为:.
9.3(答案不唯一)
解:设第三边的长为x,则
,
∴,
∴第三边的长可能是3.
故答案为:3(答案不唯一)
10.
解:由反证法的定义可知,假设需要否定结论,
所以先假设.
故答案为:.
11.2
解:∵,
∴,
解得.
故答案为:2.
12.
解:由题意得:方程组的解为,
故答案为:.
13.
解:∵,
∴,
∵
∴,
∵,
∴,
即,
故答案为:.
14.
解:
得:,
即,
∵,
∴,
解得:,
故答案为:.
15.
解:∵的解集中的最大整数解为5,
∴,
故答案为.
16.或/36或24
解:∵,
∴由三角形内角和知
由题意直线交边于点D,
则分以下两大类情况:
①当是钝角三角形时,如图1和图2,
在中,由,
则,
又,,
∴,
∴.
②当是锐角三角形时,如图3和图4,
在中,由,
则,
则,
∴.
综上所述,或.
故答案为:或.
17.(1)
(2)
(1)解:
;
(2)解:
.
18.(1)
(2)
(1)解:
;
(2)解:
.
19.(1)
(2)
(1)解:
得,
解得:,
将代入得,
解得,
∴;
(2)
解不等式得,
解不等式得,
∴原不等式组的解集为.
20.(1)画图见解析;
(2).
(1)解:如图,点和点的位置判断出平移方式为向右平移个单位长度,向下平移个单位长度,据此确定的位置,然后顺次连接;
∴即为所求;
(2)解:如图,连接,
扫过的面积是
,
故答案为:.
21.(1)
(2),
(1)解∶ 二元一次方程变形为,
∴二元一次方程的伴随数是,
故答案为∶ ;
(2)解:∵关于x、y的二元一次方程的伴随数是,
∴原方程为,
∵,是方程的两组解,
∴,
解得.
22.(1)见解析
(2)
(1)证明:∵,,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,,
∴.
23.(1)甲水果进价为15元/千克;乙水果进价为26元/千克
(2)购进的甲种水果至少为60千克
(1)解:设甲种水果的进价是每千克x元,乙种水果的进价是每千克y元,
由题意得:,
解得:,
答:甲水果进价为15元/千克;乙水果进价为26元/千克;
(2)设第三次购进的甲种水果为m千克,则乙种水果为千克,
由题意得: ,
解得:,
答:第三次购进的甲种水果至少为60千克.
24.(1);
(2).
(1)解:
,
∵的结果不含的一次项,
∴,
∴;
(2)解:∵,,
∴,
∴,
∵是不等式的解,不是不等式的解,
∴,
∴,
∴整数的值为.
25.(1)见解析
(2)①9;②小亮说法正确,见解析
(1)证明:∵,
∴,
∵,
∴,
∴,
∴;
(2)①证明:设的交点为点M,
∵,,
∴,
∵,
∴,
∵,
∴,
∴.
∵,,
∴.
②解:作的垂直平分线,将沿着第一次轴对称,得到;
连接,过作的垂线,由,则为的垂直平分线,将沿着第二次轴对称,得到,如图,则直线,即为所求.
26.(1)见解析;(2)假命题,逆命题:如果一个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍,那么这个三位数能被3整除;(3)1203;(4)15或39
解:(1)∵可以被3整除,
∴设(k为正整数)
∴,
∵为整数,
∴可以被3整除,
(2)命题2是假命题,理由如下:
例如能被3整除,但是;
逆命题:如果一个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍,那么这个三位数能被3整除;
(3)∵四位数能被3整除,
∴能被3整除,
∴能被3整除,
∵能被3整除,
∴能被3整除;
设(k为正整数),
∵,
∴,
∴,
∵要使这个四位数最小,
∴首先要满足a最小,
当的同时,要满足b最小,则此时,
∴,
∴当,时,这个四位数最小,最小为1203;
(4)设第一次看到的两位数为,则第二次看到的两位数为,第三次看到的三位数为
∵可以被3整除,
∴设(k为正整数)
∵可以被3整除
∴可以被3整除,
∵后,看到里程碑上的两位数与第一次看到的两位数恰好互换了两个数字的位置,
∴汽车的速度为,
∵再过,看到里程碑上的数是第一次看到的两位数的两个数字之间添加一个数字m所得的三位数,
∴,
∴,
∵m为整数且,
∴一定是大于等于0的偶数,
当时,,则,
∵,
∴,
∴a一定是3的倍数,
∴,
∴,
∴;
当时,,则,
∵,
∴,
∴一定是3的倍数,
∴,
∴,
∴;
综上所述,第一次看到的里程碑上的两位数是15或39.
一、单选题
1.下列计算正确的是( )
A. B.
C. D.
2.用不等式表示图中的解集,下列正确的是( )
A. B. C. D.
3.如图,和相交于点,若,用“”证明还需( )
A. B. C. D.
4.在国内投寄一封平信应付邮资如下表:
信件质量(克)
邮资(元/封)
某人投寄一封平信花费元,则此平信的质量可能为( )
A.克 B.克 C.克 D.克
5.要说明命题“若,则”是假命题,能举的一个反例是( )
A., B., C., D.,
6.如图,为的中线,将沿翻折,使点B落在点E处,与边交于点F.记的面积为,的面积为,要想求的值,只要知道( )
A.的面积 B.的面积
C.的面积 D.四边形的面积
二、填空题
7.用科学记数法表示为 .
8.“a的一半与3的和小于2”用不等式表示为 .
9.若三角形两边分别为5和7,则第三边的长可能是 .(写出一个符合条件的值即可)
10.用反证法证明“在中,若,则”,第一步应假设 .
11.若,则m为 .
12.如图,表1的每对,的值都是二元一次方程的解,表2的每对,的值都是二元一次方程的解,则方程组的解为 .
表1
x 0 1
y 0
表2
x 0 1
y 1
13.如图,中,点D,E分别在边,上,若,则的度数为 .
14.关于x,y的方程组的解满足不等式,则m的取值范围是 .
15.若的解集中的最大整数解为5,则a的取值范围是 .
16.在中,,E,F分别为直线和直线上的点,直线交边于点D,,,则 .
三、解答题
17.计算或化简:
(1)
(2)
18.计算或化简:
(1)
(2)
19.解方程组或不等式组
(1)解方程组:
(2)解不等式组:
20.正方形网格中的每个小正方形的边长均为个单位长度,各顶点的位置如图所示.将平移,使点移到点,点分别是的对应点.
(1)画出平移后的;
(2)在整个平移的过程中,扫过的面积是______.
21.我们把关于x、y的二元一次方程的系数a、b、c称为该方程的伴随数,记作.例如:二元一次方程的伴随数是.
(1)二元一次方程的伴随数是__________
(2)已知关于x、y的二元一次方程的伴随数是,且,是该方程的两组解,求m、n的值.
22.如图,、为两条线段,E为线段上方一点,连结交AB于F,过点E作直线交,于G,H,.
(1)求证:;
(2)若,求的度数.
23.某水果店经销甲、乙两种水果,两次购进水果的情况如表所示(两次进货时,两种水果的进价保持不变):
进货批次 甲种水果(单位:千克) 乙种水果(单位:千克) 总费用(单位:元)
第一次 80 50 2500
第二次 40 70 2420
(1)求甲、乙两种水果的进价;
(2)第一次和第二次购进的水果全部售完后,在两种水果进价不变的情况下,第三次又购进甲、乙两种水果共150千克,购买的资金不超过3240元,则第三次购进的甲种水果至少为多少千克?
24.已知代数式,,其中,为常数.
(1)若与的乘积化简后不含的一次项,求的值(用含的代数式表示);
(2)在()的条件下,是不等式的解,不是不等式的解,求整数的值.
25.如图1,在直角中,,D为上一点,E为外一点,,,.
(1)求证:;
(2)若(如图2),点F在线段上,.
①当时,求的面积;
②小亮说:可以看作由经过两次轴对称变换得到.他的说法是否正确,若正确,用圆规和没有刻度的直尺在图3中作出两条对称轴(若有多种情况,作出一种情况即可);若不正确,请写出一种正确的变换方式.
26.阅读下面材料,并按要求完成相应的任务:
如何快速判断一个较为复杂的整数能否被3整除?小明对下列一些能被3整除的整数进行了研究:27,123,159,246,1233,23454. 小明通过观察、计算发现:这些整数各个数位上的数字之和都能被3整除,如:整数246各个数位上的数字之和为,12能被3整除;整数1233各个数位上的数字之和为,9能被3整除.由此,他提出了这样一个命题; 命题1:如果一个数能被3整除,那么这个数各个数位上的数字之和能被3整除.小明以两位数为例进行了证明; 设是一个两位数,若两位数能被3整除,求证:能被3整除. 证明:∵两位数能被3整除, ∴设(k为正整数)... .为整数.可以被3整除. 由此推断,命题1是一个真命题,紧接着对它的逆命题进行了研究,发现命题1的逆命题也是真命题. 结论:在判断一个数是否能被3整除时,可以通过计算其各个数位上数字之和来进行快速判断. 小明在研究时还发现,整数123中,;整数159中,;整数246中,.于是,他又提出了这样一个命题; 命题2:如果一个三位数能被3整除,那么这个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍.
任务1:证明命题
(1)设是一个三位数,若可以被3整除,求证:这个三位数也能被3整除.
任务2:写逆命题
(2)判断命题2是真命题还是假命题,并写出它的逆命题;
任务3:应用结论
(3)若四位数能被3整除,且,这个四位数的最小值为______.
(4)小亮在匀速行驶的汽车里,注意到公路里程碑上的数是一个能被3整除的两位数;后,看到里程碑上的两位数与第一次看到的两位数恰好互换了两个数字的位置;再过,看到里程碑上的数是第一次看到的两位数的两个数字之间添加一个数字m所得的三位数,且这个三位数也能被3整除.则第一次看到的里程碑上的两位数是多少?
参考答案
1.A
解:A.,计算正确,故此选项符合题意;
B.,计算错误,故此选项不符合题意;
C.,计算错误,故此选项不符合题意;
D.,计算错误,故此选项不符合题意;
故选A.
2.B
解:由数轴可得:,
故选:B.
3.B
解:在和中,,,
若要用证明,则需要添加条件,
故选:.
4.C
解:由表格可知,当信件质量满足时,邮资为元,
∴此平信的质量可能为克,
故选:.
5.D
解:当,时,,而,
∴命题“若,则”是假命题,
故选:D.
6.C
解:∵为的中线,
∴,
由折叠的性质得:,
∴,
∵,,,
∴,
∴想求的值,只要知道的面积即可,
故选:C.
7.
解:∵,
故答案为:.
8.
解:由题意得,.
故答案为:.
9.3(答案不唯一)
解:设第三边的长为x,则
,
∴,
∴第三边的长可能是3.
故答案为:3(答案不唯一)
10.
解:由反证法的定义可知,假设需要否定结论,
所以先假设.
故答案为:.
11.2
解:∵,
∴,
解得.
故答案为:2.
12.
解:由题意得:方程组的解为,
故答案为:.
13.
解:∵,
∴,
∵
∴,
∵,
∴,
即,
故答案为:.
14.
解:
得:,
即,
∵,
∴,
解得:,
故答案为:.
15.
解:∵的解集中的最大整数解为5,
∴,
故答案为.
16.或/36或24
解:∵,
∴由三角形内角和知
由题意直线交边于点D,
则分以下两大类情况:
①当是钝角三角形时,如图1和图2,
在中,由,
则,
又,,
∴,
∴.
②当是锐角三角形时,如图3和图4,
在中,由,
则,
则,
∴.
综上所述,或.
故答案为:或.
17.(1)
(2)
(1)解:
;
(2)解:
.
18.(1)
(2)
(1)解:
;
(2)解:
.
19.(1)
(2)
(1)解:
得,
解得:,
将代入得,
解得,
∴;
(2)
解不等式得,
解不等式得,
∴原不等式组的解集为.
20.(1)画图见解析;
(2).
(1)解:如图,点和点的位置判断出平移方式为向右平移个单位长度,向下平移个单位长度,据此确定的位置,然后顺次连接;
∴即为所求;
(2)解:如图,连接,
扫过的面积是
,
故答案为:.
21.(1)
(2),
(1)解∶ 二元一次方程变形为,
∴二元一次方程的伴随数是,
故答案为∶ ;
(2)解:∵关于x、y的二元一次方程的伴随数是,
∴原方程为,
∵,是方程的两组解,
∴,
解得.
22.(1)见解析
(2)
(1)证明:∵,,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∵,,
∴.
23.(1)甲水果进价为15元/千克;乙水果进价为26元/千克
(2)购进的甲种水果至少为60千克
(1)解:设甲种水果的进价是每千克x元,乙种水果的进价是每千克y元,
由题意得:,
解得:,
答:甲水果进价为15元/千克;乙水果进价为26元/千克;
(2)设第三次购进的甲种水果为m千克,则乙种水果为千克,
由题意得: ,
解得:,
答:第三次购进的甲种水果至少为60千克.
24.(1);
(2).
(1)解:
,
∵的结果不含的一次项,
∴,
∴;
(2)解:∵,,
∴,
∴,
∵是不等式的解,不是不等式的解,
∴,
∴,
∴整数的值为.
25.(1)见解析
(2)①9;②小亮说法正确,见解析
(1)证明:∵,
∴,
∵,
∴,
∴,
∴;
(2)①证明:设的交点为点M,
∵,,
∴,
∵,
∴,
∵,
∴,
∴.
∵,,
∴.
②解:作的垂直平分线,将沿着第一次轴对称,得到;
连接,过作的垂线,由,则为的垂直平分线,将沿着第二次轴对称,得到,如图,则直线,即为所求.
26.(1)见解析;(2)假命题,逆命题:如果一个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍,那么这个三位数能被3整除;(3)1203;(4)15或39
解:(1)∵可以被3整除,
∴设(k为正整数)
∴,
∵为整数,
∴可以被3整除,
(2)命题2是假命题,理由如下:
例如能被3整除,但是;
逆命题:如果一个三位数的百位上的数字与个位上的数字之和等于十位上的数字的两倍,那么这个三位数能被3整除;
(3)∵四位数能被3整除,
∴能被3整除,
∴能被3整除,
∵能被3整除,
∴能被3整除;
设(k为正整数),
∵,
∴,
∴,
∵要使这个四位数最小,
∴首先要满足a最小,
当的同时,要满足b最小,则此时,
∴,
∴当,时,这个四位数最小,最小为1203;
(4)设第一次看到的两位数为,则第二次看到的两位数为,第三次看到的三位数为
∵可以被3整除,
∴设(k为正整数)
∵可以被3整除
∴可以被3整除,
∵后,看到里程碑上的两位数与第一次看到的两位数恰好互换了两个数字的位置,
∴汽车的速度为,
∵再过,看到里程碑上的数是第一次看到的两位数的两个数字之间添加一个数字m所得的三位数,
∴,
∴,
∵m为整数且,
∴一定是大于等于0的偶数,
当时,,则,
∵,
∴,
∴a一定是3的倍数,
∴,
∴,
∴;
当时,,则,
∵,
∴,
∴一定是3的倍数,
∴,
∴,
∴;
综上所述,第一次看到的里程碑上的两位数是15或39.
同课章节目录
