第二章 几何图形的初步认识 滚动练习三 (2.1~2.4) (含答案) 2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 第二章 几何图形的初步认识 滚动练习三 (2.1~2.4) (含答案) 2025-2026学年数学冀教版(2024)七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 127.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览


文档简介
滚动练习三 (2.1~2.4)
一、选择题
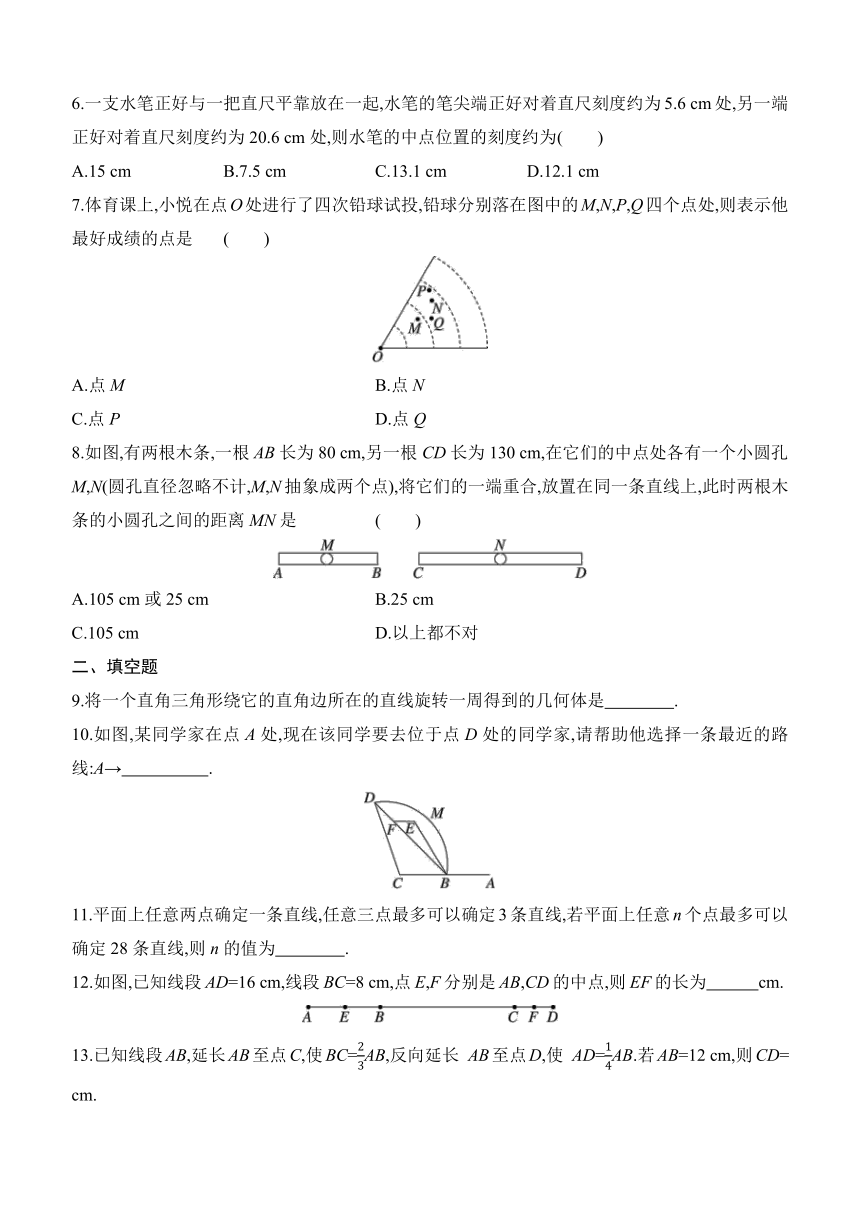
1.(2025保定期中)下面几种图形中,平面图形有( )
A.1个 B.2个 C.3个 D.4个
2.在下列现象中,不可以用基本事实“两点确定一条直线”来解释的有 ( )
A.1个 B.2个 C.3个 D.4个
3.(2025许昌襄城县期末)如图,小轩同学根据图形写出了四个结论:①图中共有2条直线;②图中共有7条射线;③图中共有6条线段;④图中射线BD与射线CD是同一条射线.其中结论错误的是 ( )
A.①③④ B.①②③ C.②③④ D.①②④
4.把两条线段AB和CD放在同一条直线上比较长短时,下列说法错误的是 ( )
A.如果线段AB的两个端点均落在线段CD的内部,那么ABB.如果点A,C重合,点B落在线段CD的内部,那么ABC.如果线段AB的一个端点在线段CD的内部,另一个端点在线段CD的外部,那么AB>CD
D.如果点B,D重合,点A,C位于点B的同侧,且点A落在线段CD的外部,那么AB>CD
5.如图,下列关系式中与下图不一定相符的是 ( )
A.AD-CD=AB+BC B.AC-BC=AD-BD
C.AC-BC=BD-BC D.AC-AB=BD-CD
6.一支水笔正好与一把直尺平靠放在一起,水笔的笔尖端正好对着直尺刻度约为5.6 cm处,另一端正好对着直尺刻度约为20.6 cm处,则水笔的中点位置的刻度约为 ( )
A.15 cm B.7.5 cm C.13.1 cm D.12.1 cm
7.体育课上,小悦在点O处进行了四次铅球试投,铅球分别落在图中的M,N,P,Q四个点处,则表示他最好成绩的点是 ( )
A.点M B.点N
C.点P D.点Q
8.如图,有两根木条,一根AB长为80 cm,另一根CD长为130 cm,在它们的中点处各有一个小圆孔M,N(圆孔直径忽略不计,M,N抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离MN是 ( )
A.105 cm或25 cm B.25 cm
C.105 cm D.以上都不对
二、填空题
9.将一个直角三角形绕它的直角边所在的直线旋转一周得到的几何体是 .
10.如图,某同学家在点A处,现在该同学要去位于点D处的同学家,请帮助他选择一条最近的路线:A→ .
11.平面上任意两点确定一条直线,任意三点最多可以确定3条直线,若平面上任意n个点最多可以确定28条直线,则n的值为 .
12.如图,已知线段AD=16 cm,线段BC=8 cm,点E,F分别是AB,CD的中点,则EF的长为 cm.
13.已知线段AB,延长AB至点C,使BC=AB,反向延长 AB至点D,使 AD=AB.若AB=12 cm,则CD= cm.
三、解答题
14.如图,已知A,B,C,D四点,请按要求画图.(保留画图痕迹)
(1)画直线AB.
(2)画射线AC.
(3)连接BD,交AC于点P.
(4)连接BC,并延长BC到点E,使得CE=AB+BC.
15.如图,A,B,C,D四点在一条直线上.
(1)图中共有 条线段.
(2)AD= + + .
(3)BC+CD= -AB.
(4)若C是BD的中点,AD=16 cm,AB=2BC,求线段AC的长.
16.观察图形,回答下列问题:
(1)图1是由几个面组成的 这些面有什么特征
(2)图2是由几个面组成的 这些面有什么特征
(3)图1中面与面相交共形成了多少条线 这些线都是直的吗 图2呢
(4)图1和图2中各有几个顶点
17.在如图所示的数轴上,某点从原点开始运动,先向左平移2个单位长度到达点A,再向左平移4个单位长度到达点B,最后向右平移10个单位长度到达点C.
(1)分别写出点A,B,C表示的数.
(2)若点P在线段BC上运动,当BP=3AP时,求出点P表示的数.
(3)若点Q从点C出发,在线段BC的延长线上运动,M是BQ的中点,N是CQ的中点,试说明BM-CN是一个定值.
【详解答案】
1.B 解析:三角形、正方形是平面图形,正方体和球是立体图形,因此平面图形有2个.故选B.
2.A 解析:可以用基本事实“两点确定一条直线”来解释的有木匠弹墨线、打靶瞄准、拉绳插秧;“弯曲公路改直”,可以用“两点之间线段最短”来解释,不能用基本事实“两点确定一条直线”来解释.所以这些现象中,不可以用基本事实“两点确定一条直线”来解释的有1个.故选A.
3.D 解析:①图中只有1条直线BD,故错误;②以B,C为端点可以各引出两条射线,以D为端点可以引出3条射线,以A为端点可以引出1条射线,则图中共有2×2+3+1=8(条)射线,故错误;③图中共有6条线段,即线段AB,AC,AD,BC,BD,CD,故正确;④图中射线BD与射线CD不是同一条射线,故错误.所以错误的有①②④.故选D.
4.C 解析:A.如果线段AB的两个端点均落在线段CD的内部,那么ABCD,故本选项正确,不符合题意.故选C.
5.C 解析:A.AD-CD=AB+BC,正确,不符合题意;B.AC-BC=AD-BD,正确,不符合题意;C.AC-BC=AB,而BD-BC=CD,故本选项错误,符合题意;D.AC-AB=BD-CD,正确,不符合题意.故选C.
6.C 解析:因为水笔的笔尖端正好对着直尺刻度约为5.6 cm处,另一端正好对着直尺刻度约为20.6 cm处,所以水笔的长度为20.6-5.6=15(cm),水笔的一半的长度为15÷2=7.5(cm),所以水笔的中点位置的刻度约为5.6+7.5 =13.1(cm).故选C.
7.C 解析:如图所示,OP>ON>OQ>OM,
所以表示他最好成绩的点是点P.故选C.
8.A 解析:本题有两种情形(木条抽象成线段):
(1)当A,C(或B,D)重合,且剩余两端点在重合点同侧时,如图1,
所以MN=CN-AM=CD-AB=65-40=25(cm).
(2)当B,C(或A,D)重合,且剩余两端点在重合点两侧时,如图2,
所以MN=CN+BM=CD+AB=65+40=105(cm).综上所述,两根木条的小圆孔之间的距离MN是25 cm或105 cm.故选A.
9.圆锥 解析:根据题意可知,得到的几何体是圆锥.
10.B→F→D 解析:根据两点之间线段最短,可得B,D两点之间的最短距离是线段BD的长度,所以最近的路线是A→B→F→D.
11.8 解析:两点确定一条直线;任意三点最多可确定3条直线;任意4点最多可确定(1+2+3)条直线,任意5点最多可确定(1+2+3+4)条直线,因为1+2+3+4+5+6+7=28,所以平面上任意8个点最多可确定28条直线.
12.12 解析:因为点E,F分别是AB,CD的中点,所以AE=BE=AB,CF=DF=CD,因为AD=16 cm,BC=8 cm,而AD=AB+BC+CD,所以AB+CD=16-8=8(cm),所以BE+CF=(AB+CD)=4(cm),所以EF=EB+BC+CF=4+8=12(cm).
13.23 解析:如图:
因为AB=12 cm,所以BC=AB=8 cm,AD=AB=3 cm,所以CD=DA+AB+BC=3+12+8=23(cm).
14.解:(1)(2)(3)(4)如图所示.
15.解:(1)6
(2)AB BC CD
(3)AD
(4)因为C是BD的中点,所以BC=CD=BD.因为AB=2BC,AD=AB+BC+CD,AD=16 cm,所以2BC+BC+BC=16 cm.所以BC=4 cm.所以AB=2BC=8 cm.所以AC=AB+BC=12 cm.
16.解:(1)图1是由6个面组成的,这些面都是平的面.
(2)图2是由2个面组成的,其中一个是平的面,一个是曲的面.
(3)图1中面与面相交共形成了12条线,这些线都是直的,图2中面与面相交形成了1条线,不是直的,是曲的线.
(4)图1中有8个顶点,图2中只有1个顶点.
17.解:(1)点A表示的数为-2,
点B表示的数为-6,
点C表示的数为4.
(2)可分为以下两种情况讨论:
①当点P在线段AB上时,BP+AP=AB=4.
因为BP=3AP,
所以3AP+AP=4,
解得AP=1,
所以点P表示的数为-3.
②当点P在线段AC上时,BP-AP=AB=4.
因为BP=3AP,
所以3AP-AP=4,
解得AP=2,
所以点P表示的数为0,
综上所述,点P表示的数为-3或0.
(3)设点Q表示的数为m,则BQ=m-(-6)=m+6,CQ=m-4.
因为M是BQ的中点,N是CQ的中点,
所以BM=BQ=,CN=CQ=,
所以BM-CN==5,
所以BM-CN是一个定值.
一、选择题
1.(2025保定期中)下面几种图形中,平面图形有( )
A.1个 B.2个 C.3个 D.4个
2.在下列现象中,不可以用基本事实“两点确定一条直线”来解释的有 ( )
A.1个 B.2个 C.3个 D.4个
3.(2025许昌襄城县期末)如图,小轩同学根据图形写出了四个结论:①图中共有2条直线;②图中共有7条射线;③图中共有6条线段;④图中射线BD与射线CD是同一条射线.其中结论错误的是 ( )
A.①③④ B.①②③ C.②③④ D.①②④
4.把两条线段AB和CD放在同一条直线上比较长短时,下列说法错误的是 ( )
A.如果线段AB的两个端点均落在线段CD的内部,那么AB
D.如果点B,D重合,点A,C位于点B的同侧,且点A落在线段CD的外部,那么AB>CD
5.如图,下列关系式中与下图不一定相符的是 ( )
A.AD-CD=AB+BC B.AC-BC=AD-BD
C.AC-BC=BD-BC D.AC-AB=BD-CD
6.一支水笔正好与一把直尺平靠放在一起,水笔的笔尖端正好对着直尺刻度约为5.6 cm处,另一端正好对着直尺刻度约为20.6 cm处,则水笔的中点位置的刻度约为 ( )
A.15 cm B.7.5 cm C.13.1 cm D.12.1 cm
7.体育课上,小悦在点O处进行了四次铅球试投,铅球分别落在图中的M,N,P,Q四个点处,则表示他最好成绩的点是 ( )
A.点M B.点N
C.点P D.点Q
8.如图,有两根木条,一根AB长为80 cm,另一根CD长为130 cm,在它们的中点处各有一个小圆孔M,N(圆孔直径忽略不计,M,N抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离MN是 ( )
A.105 cm或25 cm B.25 cm
C.105 cm D.以上都不对
二、填空题
9.将一个直角三角形绕它的直角边所在的直线旋转一周得到的几何体是 .
10.如图,某同学家在点A处,现在该同学要去位于点D处的同学家,请帮助他选择一条最近的路线:A→ .
11.平面上任意两点确定一条直线,任意三点最多可以确定3条直线,若平面上任意n个点最多可以确定28条直线,则n的值为 .
12.如图,已知线段AD=16 cm,线段BC=8 cm,点E,F分别是AB,CD的中点,则EF的长为 cm.
13.已知线段AB,延长AB至点C,使BC=AB,反向延长 AB至点D,使 AD=AB.若AB=12 cm,则CD= cm.
三、解答题
14.如图,已知A,B,C,D四点,请按要求画图.(保留画图痕迹)
(1)画直线AB.
(2)画射线AC.
(3)连接BD,交AC于点P.
(4)连接BC,并延长BC到点E,使得CE=AB+BC.
15.如图,A,B,C,D四点在一条直线上.
(1)图中共有 条线段.
(2)AD= + + .
(3)BC+CD= -AB.
(4)若C是BD的中点,AD=16 cm,AB=2BC,求线段AC的长.
16.观察图形,回答下列问题:
(1)图1是由几个面组成的 这些面有什么特征
(2)图2是由几个面组成的 这些面有什么特征
(3)图1中面与面相交共形成了多少条线 这些线都是直的吗 图2呢
(4)图1和图2中各有几个顶点
17.在如图所示的数轴上,某点从原点开始运动,先向左平移2个单位长度到达点A,再向左平移4个单位长度到达点B,最后向右平移10个单位长度到达点C.
(1)分别写出点A,B,C表示的数.
(2)若点P在线段BC上运动,当BP=3AP时,求出点P表示的数.
(3)若点Q从点C出发,在线段BC的延长线上运动,M是BQ的中点,N是CQ的中点,试说明BM-CN是一个定值.
【详解答案】
1.B 解析:三角形、正方形是平面图形,正方体和球是立体图形,因此平面图形有2个.故选B.
2.A 解析:可以用基本事实“两点确定一条直线”来解释的有木匠弹墨线、打靶瞄准、拉绳插秧;“弯曲公路改直”,可以用“两点之间线段最短”来解释,不能用基本事实“两点确定一条直线”来解释.所以这些现象中,不可以用基本事实“两点确定一条直线”来解释的有1个.故选A.
3.D 解析:①图中只有1条直线BD,故错误;②以B,C为端点可以各引出两条射线,以D为端点可以引出3条射线,以A为端点可以引出1条射线,则图中共有2×2+3+1=8(条)射线,故错误;③图中共有6条线段,即线段AB,AC,AD,BC,BD,CD,故正确;④图中射线BD与射线CD不是同一条射线,故错误.所以错误的有①②④.故选D.
4.C 解析:A.如果线段AB的两个端点均落在线段CD的内部,那么AB
5.C 解析:A.AD-CD=AB+BC,正确,不符合题意;B.AC-BC=AD-BD,正确,不符合题意;C.AC-BC=AB,而BD-BC=CD,故本选项错误,符合题意;D.AC-AB=BD-CD,正确,不符合题意.故选C.
6.C 解析:因为水笔的笔尖端正好对着直尺刻度约为5.6 cm处,另一端正好对着直尺刻度约为20.6 cm处,所以水笔的长度为20.6-5.6=15(cm),水笔的一半的长度为15÷2=7.5(cm),所以水笔的中点位置的刻度约为5.6+7.5 =13.1(cm).故选C.
7.C 解析:如图所示,OP>ON>OQ>OM,
所以表示他最好成绩的点是点P.故选C.
8.A 解析:本题有两种情形(木条抽象成线段):
(1)当A,C(或B,D)重合,且剩余两端点在重合点同侧时,如图1,
所以MN=CN-AM=CD-AB=65-40=25(cm).
(2)当B,C(或A,D)重合,且剩余两端点在重合点两侧时,如图2,
所以MN=CN+BM=CD+AB=65+40=105(cm).综上所述,两根木条的小圆孔之间的距离MN是25 cm或105 cm.故选A.
9.圆锥 解析:根据题意可知,得到的几何体是圆锥.
10.B→F→D 解析:根据两点之间线段最短,可得B,D两点之间的最短距离是线段BD的长度,所以最近的路线是A→B→F→D.
11.8 解析:两点确定一条直线;任意三点最多可确定3条直线;任意4点最多可确定(1+2+3)条直线,任意5点最多可确定(1+2+3+4)条直线,因为1+2+3+4+5+6+7=28,所以平面上任意8个点最多可确定28条直线.
12.12 解析:因为点E,F分别是AB,CD的中点,所以AE=BE=AB,CF=DF=CD,因为AD=16 cm,BC=8 cm,而AD=AB+BC+CD,所以AB+CD=16-8=8(cm),所以BE+CF=(AB+CD)=4(cm),所以EF=EB+BC+CF=4+8=12(cm).
13.23 解析:如图:
因为AB=12 cm,所以BC=AB=8 cm,AD=AB=3 cm,所以CD=DA+AB+BC=3+12+8=23(cm).
14.解:(1)(2)(3)(4)如图所示.
15.解:(1)6
(2)AB BC CD
(3)AD
(4)因为C是BD的中点,所以BC=CD=BD.因为AB=2BC,AD=AB+BC+CD,AD=16 cm,所以2BC+BC+BC=16 cm.所以BC=4 cm.所以AB=2BC=8 cm.所以AC=AB+BC=12 cm.
16.解:(1)图1是由6个面组成的,这些面都是平的面.
(2)图2是由2个面组成的,其中一个是平的面,一个是曲的面.
(3)图1中面与面相交共形成了12条线,这些线都是直的,图2中面与面相交形成了1条线,不是直的,是曲的线.
(4)图1中有8个顶点,图2中只有1个顶点.
17.解:(1)点A表示的数为-2,
点B表示的数为-6,
点C表示的数为4.
(2)可分为以下两种情况讨论:
①当点P在线段AB上时,BP+AP=AB=4.
因为BP=3AP,
所以3AP+AP=4,
解得AP=1,
所以点P表示的数为-3.
②当点P在线段AC上时,BP-AP=AB=4.
因为BP=3AP,
所以3AP-AP=4,
解得AP=2,
所以点P表示的数为0,
综上所述,点P表示的数为-3或0.
(3)设点Q表示的数为m,则BQ=m-(-6)=m+6,CQ=m-4.
因为M是BQ的中点,N是CQ的中点,
所以BM=BQ=,CN=CQ=,
所以BM-CN==5,
所以BM-CN是一个定值.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
