第二章 几何图形的初步认识 评估测试卷(含答案)2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 第二章 几何图形的初步认识 评估测试卷(含答案)2025-2026学年数学冀教版(2024)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 191.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览



文档简介
第二章 几何图形的初步认识 评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列物体中,类似于圆锥的是 ( )
A.水杯 B.漏斗
C.铅笔盒 D.足球
2.毛泽东主席在《水调歌头·游泳》中写道“一桥飞架南北,天堑变通途”.正如从黄果树风景区到关岭县城的坝陵河大桥建成后,从黄果树风景区到关岭县城经大桥通过的路程缩短20 km,用所学数学知识解释这一现象恰当的是 ( )
A.过一点可以画多条直线
B.两点确定一条直线
C.两点之间线段最短
D.连接两点间线段的长度是两点间的距离
3.如图,点A,B,C在直线l上,下列说法正确的是 ( )
A.点C在线段AB上
B.点A在线段BC的延长线上
C.射线BC与射线CB是同一条射线
D.AC=BC+AB
4.如图,图中共有线段 ( )
A.5条 B.6条 C.7条 D.8条
5.如图所示,把图形绕着给定的直线旋转一周后形成的几何体是 ( )
A B C D
6.将一副直角三角板按如图放置,若∠AOD=20°,则∠BOC的大小是 ( )
A.110° B.120° C.140° D.160°
7.如图,将三角形OAB绕点O顺时针旋转60°后,得到三角形OCD,下列说法正确的是 ( )
A.点B的对应点是点C B.∠AOB=60°
C.OB=CD D.∠B=∠D
8.如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧MN是 ( )
A.以点C为圆心,OE长为半径的弧
B.以点C为圆心,EF长为半径的弧
C.以点G为圆心,OE长为半径的弧
D.以点G为圆心,EF长为半径的弧
9.如图,C是线段AB的中点,D为线段CB上一点,下列等式:
①BD=AC-CD;②BC=2CD;③CD=AD-BC,其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
10.已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是 ( )
A.∠AOC=56° B.∠AOD=134°
C.∠AOC比∠COD小 D.∠BOD与∠BOC互补
11.已知点A,B,C,D在直线l上,AB=4,AC=6,D为BC的中点,则AD的长为 ( )
A.3 B.5 C.3或7 D.1或5
12.如图,已知∠AOB,以OA为边作∠AOC,使∠BOC=∠AOB,则下列结论成立的是 ( )
A.∠AOC=∠BOC
B.∠AOC<∠AOB
C.∠AOC=∠BOC或∠AOC=2∠BOC
D.∠AOC=∠BOC或∠AOC=3∠BOC
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2025长春南关区期末)如图,将甲、乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是 .
14.平面内三条直线两两相交,最多有a个交点,最少有b个交点,则a+b= .
15.如图,AB=4 cm,BC=2 cm,D为AC的中点,则BD的长是 cm.
16.如图,OM平分∠AOB,ON平分∠COD.若∠MON=42°,∠BOC=5°,则∠AOD= .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)计算:
(1)89°35'+20°20'(结果用度、分、秒表示).
(2)123°24'-60°36'(结果用度表示).
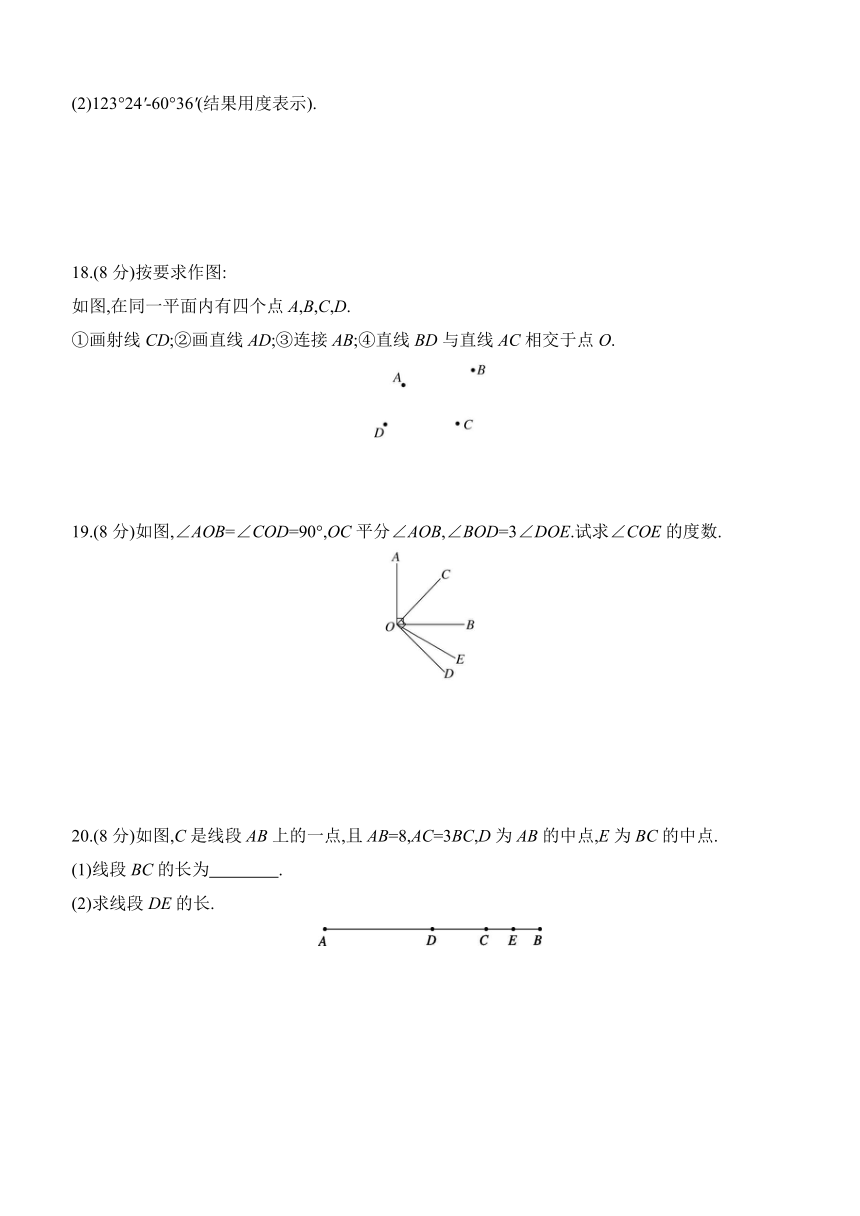
18.(8分)按要求作图:
如图,在同一平面内有四个点A,B,C,D.
①画射线CD;②画直线AD;③连接AB;④直线BD与直线AC相交于点O.
19.(8分)如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
20.(8分)如图,C是线段AB上的一点,且AB=8,AC=3BC,D为AB的中点,E为BC的中点.
(1)线段BC的长为 .
(2)求线段DE的长.
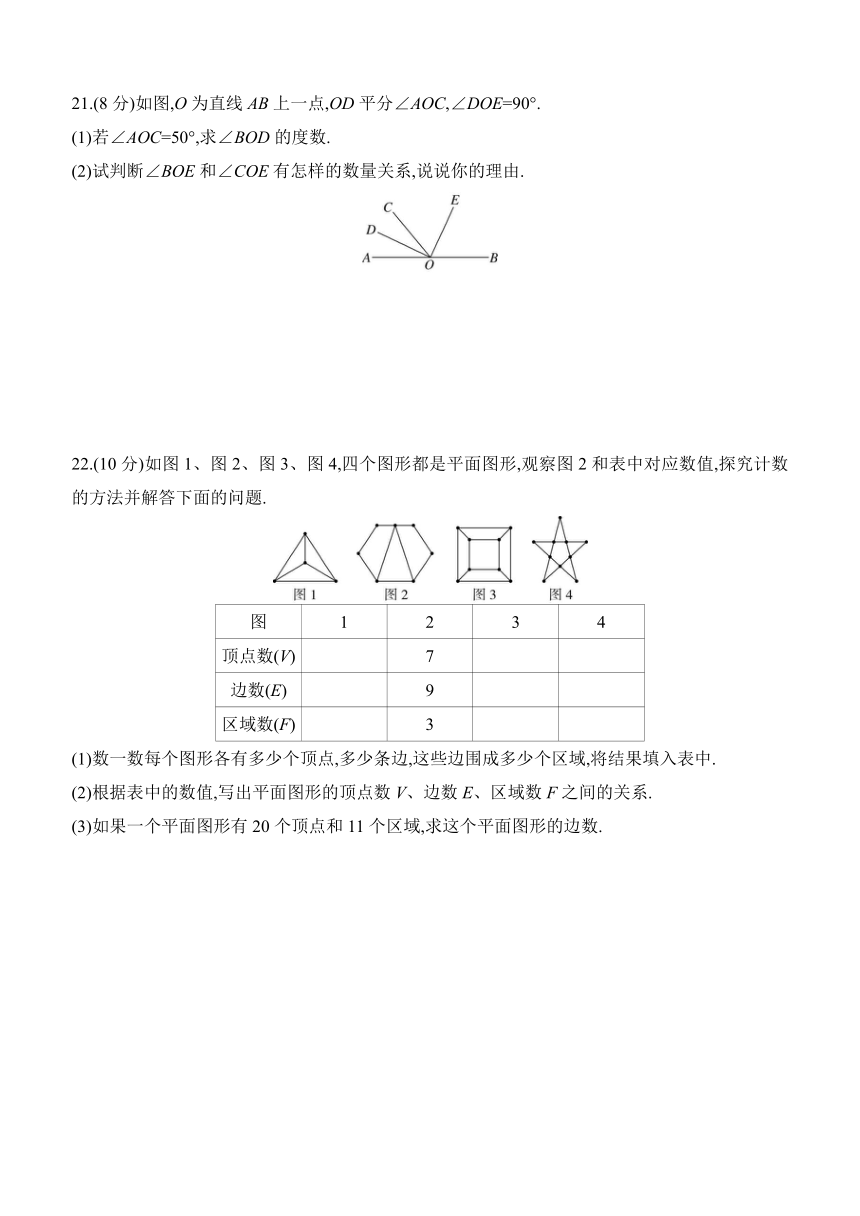
21.(8分)如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)若∠AOC=50°,求∠BOD的度数.
(2)试判断∠BOE和∠COE有怎样的数量关系,说说你的理由.
22.(10分)如图1、图2、图3、图4,四个图形都是平面图形,观察图2和表中对应数值,探究计数的方法并解答下面的问题.
图 1 2 3 4
顶点数(V) 7
边数(E) 9
区域数(F) 3
(1)数一数每个图形各有多少个顶点,多少条边,这些边围成多少个区域,将结果填入表中.
(2)根据表中的数值,写出平面图形的顶点数V、边数E、区域数F之间的关系.
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
23.(11分)如图,已知数轴上有两点A,B,它们对应的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹).
(2)若点C对应的数为c,点D对应的数为d,且AB=20,求c,d的值.
(3)在(2)的条件下,设点M是BD的中点,N是线段CD上一点,且CN=2DN,请直接写出MN的长.
24.(13分)如图1,将一块直角三角板的直角顶点O放置于直线MN上,直角边OA与直线MN重合,其中∠AOB=90°,然后将三角板AOB绕点O顺时针旋转,设∠AOM=α,从点O引射线OC和OD,OC平分∠BON,∠BOD=∠MOB.
(1)如图2,当α=30°时,∠CON= .
(2)如图2,当0°<α<90°时,求∠COD的度数(用含α的式子表示).
(3)如图3,当90°<α<180°时,请判断∠COD-∠BON的值是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
【详解答案】
1.B 解析:A.水杯类似于圆柱,不符合题意;B.漏斗类似于圆锥,符合题意;C.铅笔盒类似于长方体,不符合题意;D.足球类似于球,不符合题意.故选B.
2.C 3.D 4.B
5.B 解析:把直角三角形绕着给定的直线旋转一周后形成的几何体是圆柱中间去掉等底等高的圆锥.故选B.
6.D
7.D 解析:由旋转可知,点B的对应点是点D,∠AOC=60°,OB=OD,∠B=∠D,因此A,B,C错误,D正确.故选D.
8.D 解析:作∠PCD=∠AOB的步骤为:以点O为圆心,以任意长为半径画弧,分别交OB,OA于点E,F,再以点C为圆心,以OE长为半径画弧,交CD于点G,以点G为圆心,EF长为半径画弧,与已画的弧交于点P,作射线CP即可.所以弧MN是以点G为圆心,EF长为半径的弧.故选D.
9.C 解析:因为C是线段AB的中点,所以AC=BC,BD=BC-CD=AC-CD,所以①正确;BC不一定等于2CD,所以②错误;CD=AD-AC=AD-BC,所以③正确.故选C.
10.D 解析:A.∠AOC=56°,正确;B.∠AOD=134°,正确;C.∠COD=∠AOD-∠AOC=134°-56°=78°,∠AOC<∠COD,正确;D.∠BOD=180°-∠AOD=46°,∠BOC=180°-∠AOC=124°,∠BOD与∠BOC不互补,错误,故选D.
11.D 解析:当点C在线段AB的反向延长线上时,如图1,由线段的和与差,得BC=AB+AC=4+6=10,由线段中点的性质,得BD=BC=×10=5,故AD=BD-AB=5-4=1;当点C在线段AB的延长线上时,如图2,由线段的和与差,得BC=AC-AB=6-4=2.由线段中点的性质,得CD=BD=BC=×2=1,故AD=AB+BD=4+1=5.综上所述,AD的长为1或5.故选D.
图1
图2
12.D 解析:分两种情况:当∠BOC在∠AOB的外部时,如图1:
图1
因为∠BOC=∠AOB,所以∠AOC=3∠BOC.
当∠BOC在∠AOB的内部时,如图2:
图2
因为∠BOC=∠AOB,所以∠AOC=∠BOC.故选D.
13.两点确定一条直线
14.4 解析:因为平面内三条直线两两相交,最多有3个交点,最少有1个交点,所以a+b=4.
15.1 解析:因为AB=4 cm,BC=2 cm,所以AC=AB+BC=4+2=6(cm).因为D为AC的中点,所以CD=AC=3 cm.所以BD=CD-BC=3-2=1(cm).
16.79° 解析:因为OM平分∠AOB,ON平分∠COD,所以∠AOM=∠BOM,∠CON=∠DON.因为∠MON=42°,∠BOC=5°,
所以∠MON-∠BOC=37°,即∠BOM+∠CON=37°.所以∠AOD=∠MON+∠AOM+∠DON=∠MON+∠BOM+∠CON=42°+37°=79°.
17.解:(1)89°35'+20°20'=109°55'.
(2)123°24'-60°36'
=123.4°-60.6°
=62.8°.
18.解:作图如图所示.
19.解:因为∠AOB=90°,OC平分∠AOB,
所以∠COB=∠AOB=45°,
因为∠COD=90°,
所以∠BOD=45°,
因为∠BOD=3∠DOE,
所以∠DOE=15°,
所以∠BOE=30°,
所以∠COE=∠COB+∠BOE=45°+30°=75°.
20.解:(1)2
(2)因为AB=8,D为AB的中点,
所以DB=AB=4,
由(1)可知BC=2,
所以DC=DB-BC=4-2=2,
又因为E为BC的中点,
所以CE=BC=1,
所以DE=DC+CE=2+1=3.
21.解:(1)因为OD平分∠AOC,
所以∠AOD=∠COD=∠AOC=×50°=25°.
因为∠AOD+∠BOD=180°,
所以∠BOD=180°-∠AOD=180°-25°=155°.
(2)∠BOE=∠COE,理由如下:
因为OD平分∠AOC,
所以∠AOD=∠COD,
因为∠DOE=90°,
所以∠COD+∠COE=90°,∠AOD+∠BOE=90°,所以∠BOE=∠COE.
22.解:(1)横着填:4 8 10 6 12 15 3 5 6
(2)根据表中的数据,得顶点数V、边数E、区域数F之间的关系可表示为V+F-E=1.
(3)把V=20,F=11代入(2)中关系式,得E=V+F-1=20+11-1=30.故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
23.解:(1)如图,线段BC,BD为所求线段.
(2)因为AB=20,BC=AB,BD=3AB,
所以AC=40,AD=40,
因为a=12,
所以c=12-40=-28,d=12+40=52.
(3)MN的长为.
解析:由(2)得CD=52-(-28)=80,点B对应的数为12-20=-8,
所以BD=52-(-8)=60,
因为点M是BD的中点,
所以点M对应的数为52-30=22,
因为点N在线段CD上,CN=2DN,
所以DN=CD=,
所以点N对应的数为52-,
所以MN=-22=.
故MN的长为.
24.解:(1)30°
(2)当0°<α<90°时,
因为∠AOM=α,∠AOB=90°,
所以∠BON=∠MON-∠AOM-∠AOB=180°-α-90°=90°-α,
因为OC平分∠BON,
所以∠BOC=(90°-α),
因为∠MOB=∠MOA+∠AOB=90°+α,
所以∠BOD=(90°+α),
所以∠COD=∠BOD+∠BOC=(90°+α)+(90°-α)=75°-α.
(3)是定值.
当90°<α<180°时,
因为∠BOM=360°-90°-α=270°-α,
所以∠BOD=∠BOM=(270°-α)=90°-α,
因为OC平分∠BON,∠BON=90°+α-180°=α-90°,
所以∠COB=∠BON=(α-90°)=α-45°,
所以∠COD=∠BOD+∠COB=α+45°,
所以∠COD-∠BON=(α-90°)=60°.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列物体中,类似于圆锥的是 ( )
A.水杯 B.漏斗
C.铅笔盒 D.足球
2.毛泽东主席在《水调歌头·游泳》中写道“一桥飞架南北,天堑变通途”.正如从黄果树风景区到关岭县城的坝陵河大桥建成后,从黄果树风景区到关岭县城经大桥通过的路程缩短20 km,用所学数学知识解释这一现象恰当的是 ( )
A.过一点可以画多条直线
B.两点确定一条直线
C.两点之间线段最短
D.连接两点间线段的长度是两点间的距离
3.如图,点A,B,C在直线l上,下列说法正确的是 ( )
A.点C在线段AB上
B.点A在线段BC的延长线上
C.射线BC与射线CB是同一条射线
D.AC=BC+AB
4.如图,图中共有线段 ( )
A.5条 B.6条 C.7条 D.8条
5.如图所示,把图形绕着给定的直线旋转一周后形成的几何体是 ( )
A B C D
6.将一副直角三角板按如图放置,若∠AOD=20°,则∠BOC的大小是 ( )
A.110° B.120° C.140° D.160°
7.如图,将三角形OAB绕点O顺时针旋转60°后,得到三角形OCD,下列说法正确的是 ( )
A.点B的对应点是点C B.∠AOB=60°
C.OB=CD D.∠B=∠D
8.如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧MN是 ( )
A.以点C为圆心,OE长为半径的弧
B.以点C为圆心,EF长为半径的弧
C.以点G为圆心,OE长为半径的弧
D.以点G为圆心,EF长为半径的弧
9.如图,C是线段AB的中点,D为线段CB上一点,下列等式:
①BD=AC-CD;②BC=2CD;③CD=AD-BC,其中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
10.已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是 ( )
A.∠AOC=56° B.∠AOD=134°
C.∠AOC比∠COD小 D.∠BOD与∠BOC互补
11.已知点A,B,C,D在直线l上,AB=4,AC=6,D为BC的中点,则AD的长为 ( )
A.3 B.5 C.3或7 D.1或5
12.如图,已知∠AOB,以OA为边作∠AOC,使∠BOC=∠AOB,则下列结论成立的是 ( )
A.∠AOC=∠BOC
B.∠AOC<∠AOB
C.∠AOC=∠BOC或∠AOC=2∠BOC
D.∠AOC=∠BOC或∠AOC=3∠BOC
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2025长春南关区期末)如图,将甲、乙两把尺子拼在一起,两端重合,如果甲尺经校定是直的,那么乙尺不是直的,判断依据是 .
14.平面内三条直线两两相交,最多有a个交点,最少有b个交点,则a+b= .
15.如图,AB=4 cm,BC=2 cm,D为AC的中点,则BD的长是 cm.
16.如图,OM平分∠AOB,ON平分∠COD.若∠MON=42°,∠BOC=5°,则∠AOD= .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)计算:
(1)89°35'+20°20'(结果用度、分、秒表示).
(2)123°24'-60°36'(结果用度表示).
18.(8分)按要求作图:
如图,在同一平面内有四个点A,B,C,D.
①画射线CD;②画直线AD;③连接AB;④直线BD与直线AC相交于点O.
19.(8分)如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
20.(8分)如图,C是线段AB上的一点,且AB=8,AC=3BC,D为AB的中点,E为BC的中点.
(1)线段BC的长为 .
(2)求线段DE的长.
21.(8分)如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)若∠AOC=50°,求∠BOD的度数.
(2)试判断∠BOE和∠COE有怎样的数量关系,说说你的理由.
22.(10分)如图1、图2、图3、图4,四个图形都是平面图形,观察图2和表中对应数值,探究计数的方法并解答下面的问题.
图 1 2 3 4
顶点数(V) 7
边数(E) 9
区域数(F) 3
(1)数一数每个图形各有多少个顶点,多少条边,这些边围成多少个区域,将结果填入表中.
(2)根据表中的数值,写出平面图形的顶点数V、边数E、区域数F之间的关系.
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
23.(11分)如图,已知数轴上有两点A,B,它们对应的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹).
(2)若点C对应的数为c,点D对应的数为d,且AB=20,求c,d的值.
(3)在(2)的条件下,设点M是BD的中点,N是线段CD上一点,且CN=2DN,请直接写出MN的长.
24.(13分)如图1,将一块直角三角板的直角顶点O放置于直线MN上,直角边OA与直线MN重合,其中∠AOB=90°,然后将三角板AOB绕点O顺时针旋转,设∠AOM=α,从点O引射线OC和OD,OC平分∠BON,∠BOD=∠MOB.
(1)如图2,当α=30°时,∠CON= .
(2)如图2,当0°<α<90°时,求∠COD的度数(用含α的式子表示).
(3)如图3,当90°<α<180°时,请判断∠COD-∠BON的值是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
【详解答案】
1.B 解析:A.水杯类似于圆柱,不符合题意;B.漏斗类似于圆锥,符合题意;C.铅笔盒类似于长方体,不符合题意;D.足球类似于球,不符合题意.故选B.
2.C 3.D 4.B
5.B 解析:把直角三角形绕着给定的直线旋转一周后形成的几何体是圆柱中间去掉等底等高的圆锥.故选B.
6.D
7.D 解析:由旋转可知,点B的对应点是点D,∠AOC=60°,OB=OD,∠B=∠D,因此A,B,C错误,D正确.故选D.
8.D 解析:作∠PCD=∠AOB的步骤为:以点O为圆心,以任意长为半径画弧,分别交OB,OA于点E,F,再以点C为圆心,以OE长为半径画弧,交CD于点G,以点G为圆心,EF长为半径画弧,与已画的弧交于点P,作射线CP即可.所以弧MN是以点G为圆心,EF长为半径的弧.故选D.
9.C 解析:因为C是线段AB的中点,所以AC=BC,BD=BC-CD=AC-CD,所以①正确;BC不一定等于2CD,所以②错误;CD=AD-AC=AD-BC,所以③正确.故选C.
10.D 解析:A.∠AOC=56°,正确;B.∠AOD=134°,正确;C.∠COD=∠AOD-∠AOC=134°-56°=78°,∠AOC<∠COD,正确;D.∠BOD=180°-∠AOD=46°,∠BOC=180°-∠AOC=124°,∠BOD与∠BOC不互补,错误,故选D.
11.D 解析:当点C在线段AB的反向延长线上时,如图1,由线段的和与差,得BC=AB+AC=4+6=10,由线段中点的性质,得BD=BC=×10=5,故AD=BD-AB=5-4=1;当点C在线段AB的延长线上时,如图2,由线段的和与差,得BC=AC-AB=6-4=2.由线段中点的性质,得CD=BD=BC=×2=1,故AD=AB+BD=4+1=5.综上所述,AD的长为1或5.故选D.
图1
图2
12.D 解析:分两种情况:当∠BOC在∠AOB的外部时,如图1:
图1
因为∠BOC=∠AOB,所以∠AOC=3∠BOC.
当∠BOC在∠AOB的内部时,如图2:
图2
因为∠BOC=∠AOB,所以∠AOC=∠BOC.故选D.
13.两点确定一条直线
14.4 解析:因为平面内三条直线两两相交,最多有3个交点,最少有1个交点,所以a+b=4.
15.1 解析:因为AB=4 cm,BC=2 cm,所以AC=AB+BC=4+2=6(cm).因为D为AC的中点,所以CD=AC=3 cm.所以BD=CD-BC=3-2=1(cm).
16.79° 解析:因为OM平分∠AOB,ON平分∠COD,所以∠AOM=∠BOM,∠CON=∠DON.因为∠MON=42°,∠BOC=5°,
所以∠MON-∠BOC=37°,即∠BOM+∠CON=37°.所以∠AOD=∠MON+∠AOM+∠DON=∠MON+∠BOM+∠CON=42°+37°=79°.
17.解:(1)89°35'+20°20'=109°55'.
(2)123°24'-60°36'
=123.4°-60.6°
=62.8°.
18.解:作图如图所示.
19.解:因为∠AOB=90°,OC平分∠AOB,
所以∠COB=∠AOB=45°,
因为∠COD=90°,
所以∠BOD=45°,
因为∠BOD=3∠DOE,
所以∠DOE=15°,
所以∠BOE=30°,
所以∠COE=∠COB+∠BOE=45°+30°=75°.
20.解:(1)2
(2)因为AB=8,D为AB的中点,
所以DB=AB=4,
由(1)可知BC=2,
所以DC=DB-BC=4-2=2,
又因为E为BC的中点,
所以CE=BC=1,
所以DE=DC+CE=2+1=3.
21.解:(1)因为OD平分∠AOC,
所以∠AOD=∠COD=∠AOC=×50°=25°.
因为∠AOD+∠BOD=180°,
所以∠BOD=180°-∠AOD=180°-25°=155°.
(2)∠BOE=∠COE,理由如下:
因为OD平分∠AOC,
所以∠AOD=∠COD,
因为∠DOE=90°,
所以∠COD+∠COE=90°,∠AOD+∠BOE=90°,所以∠BOE=∠COE.
22.解:(1)横着填:4 8 10 6 12 15 3 5 6
(2)根据表中的数据,得顶点数V、边数E、区域数F之间的关系可表示为V+F-E=1.
(3)把V=20,F=11代入(2)中关系式,得E=V+F-1=20+11-1=30.故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
23.解:(1)如图,线段BC,BD为所求线段.
(2)因为AB=20,BC=AB,BD=3AB,
所以AC=40,AD=40,
因为a=12,
所以c=12-40=-28,d=12+40=52.
(3)MN的长为.
解析:由(2)得CD=52-(-28)=80,点B对应的数为12-20=-8,
所以BD=52-(-8)=60,
因为点M是BD的中点,
所以点M对应的数为52-30=22,
因为点N在线段CD上,CN=2DN,
所以DN=CD=,
所以点N对应的数为52-,
所以MN=-22=.
故MN的长为.
24.解:(1)30°
(2)当0°<α<90°时,
因为∠AOM=α,∠AOB=90°,
所以∠BON=∠MON-∠AOM-∠AOB=180°-α-90°=90°-α,
因为OC平分∠BON,
所以∠BOC=(90°-α),
因为∠MOB=∠MOA+∠AOB=90°+α,
所以∠BOD=(90°+α),
所以∠COD=∠BOD+∠BOC=(90°+α)+(90°-α)=75°-α.
(3)是定值.
当90°<α<180°时,
因为∠BOM=360°-90°-α=270°-α,
所以∠BOD=∠BOM=(270°-α)=90°-α,
因为OC平分∠BON,∠BON=90°+α-180°=α-90°,
所以∠COB=∠BON=(α-90°)=α-45°,
所以∠COD=∠BOD+∠COB=α+45°,
所以∠COD-∠BON=(α-90°)=60°.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
