第二十二章 二次函数 单元试卷(含答案)2025-2026学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 单元试卷(含答案)2025-2026学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 320.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 17:36:59 | ||
图片预览




文档简介
第二十二章 二次函数 单元试卷 2025-2026学年人教版数学九年级上册
一、选择题
由二次函数 可知
A.其图象的开口向下
B.其图象的对称轴为直线
C.其顶点坐标为
D.当 时, 随 的增大而增大
抛物线 与坐标轴的交点个数是
A. B. C. D.
若抛物线 经过点 ,则 的值是
A. B. C. D.
已知二次函数的图象如图所示,则下列结论中正确的是
A. B.3是方程的一个根
C. D.当时,随的增大而减小
在同一平面直角坐标系内,一次函数 与二次函数 的图象可能是
A. B. C. D.
如图,点 , 的坐标分别为 和 ,抛物线 的顶点在线段 上运动,与 轴交于 , 两点( 在 的左侧),点 的横坐标最小值为 ,则点 的横坐标最大值为
A. B. C. D.
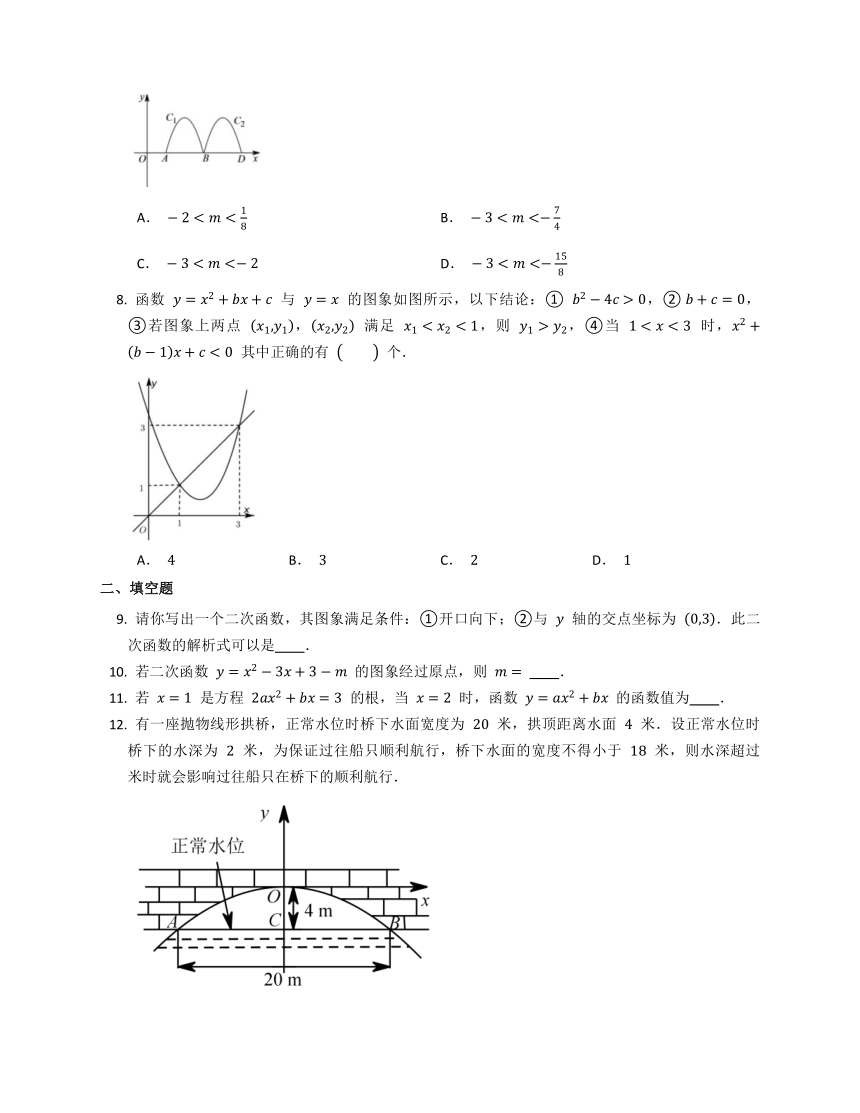
如图,抛物线 与 轴交于点 ,,把抛物线在 轴及其上方的部分记作 ,将 向右平移得 , 与 轴交于点 ,.若直线 与 , 共有 个不同的交点,则 的取值范围是
A. B.
C. D.
函数 与 的图象如图所示,以下结论:① ,② ,③若图象上两点 , 满足 ,则 ,④当 时, 其中正确的有 个.
A. B. C. D.
二、填空题
请你写出一个二次函数,其图象满足条件:①开口向下;②与 轴的交点坐标为 .此二次函数的解析式可以是 .
若二次函数 的图象经过原点,则 .
若 是方程 的根,当 时,函数 的函数值为 .
有一座抛物线形拱桥,正常水位时桥下水面宽度为 米,拱顶距离水面 米.设正常水位时桥下的水深为 米,为保证过往船只顺利航行,桥下水面的宽度不得小于 米,则水深超过 米时就会影响过往船只在桥下的顺利航行.
如图,抛物线 与直线 相交于点 ,点 ,则关于 的不等式 的解集为 .
烟花厂为咸宁温泉旅游节特别设计制作一种新型礼炮,这种礼炮的升空高 与飞行时间 的关系式是 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
若 , 是关于 的方程 的两根,且 ,则 ,,, 的大小关系是 .
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为 .
三、解答题
已知抛物线 经过点 ,,.求此抛物线的函数解析式和顶点坐标.
如图,某公司要建一个矩形的产品展示台,展示台的一边靠长为 的宣传版(这条边不能超出宣传版),另三边用总长为 的红布粘贴在展示台边上.设垂直于宣传版的一边长为 .
(1) 当展示台的面积为 时,求 的值;
(2) 设展示台的面积为 ,求 的最大值.
已知二次函数 .
(1) 判断该二次函数图象与 轴交点的个数,并说明理由.
(2) 若该二次函数的顶点坐标为 ,求 , 的值.
(3) 若把该函数图象向上平移 个单位,使得对于任意的 都有 大于 ,求征:.
某商店原来平均每天可销售某种水果 千克,每千克可盈利 元,为减少库存,经市场调查,如果这种水果每千克降价 元,则每天可所多售出 千克.
(1) 设每千克水果降价 元,平均每天盈利 元,试写出 关于 的函数表达式;
(2) 若要平均每天盈利 元,则每千克应降价多少元?
(3) 每千克降价多少元时,每天的盈利最多?最多盈利多少元?
一名大学生利用“互联网 ”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围;
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
如图 ,抛物线 与直线 相交于 , 两点,且抛物线经过点 .
(1) 求抛物线的解析式.
(2) 点 是抛物线上的一个动点(不与点 点 重合),过点 作直线 轴于点 ,交直线 于点 .当 时,求 点坐标.
(3) 如图 所示,设抛物线与 轴交于点 ,在抛物线的第一象限内,是否存在一点 ,使得四边形 的面积最大?若存在,请求出点 的坐标;若不存在,说明理由.
答案
一、选择题(共8题)
1. 【答案】B
【解析】 ,
抛物线开口向上,故A不正确;
对称轴为 ,故B正确;
当 时, 有最小值 ,故C不正确;
当 时, 随 的增大而增大,故D不正确.
2. 【答案】C
【解析】令 ,则 ,
,
二次函数 的图象与 轴有 个交点,
抛物线 与 轴有 个交点,
抛物线 与坐标轴的交点的个数是 .
3. 【答案】B
【解析】 抛物线 经过点
代入,得 ,
,
.
4. 【答案】B
【解析】【分析】根据抛物线的开口方向可得,根据抛物线对称轴可得方程的根为,;根据图象可得时,;根据抛物线可直接得到时,随的增大而增大.
【解析】解:、因为抛物线开口向下,因此,故此选项错误;
、根据对称轴为,一个交点坐标为,可得另一个与轴的交点坐标为,因此3是方程的一个根,故此选项正确;
、把代入二次函数中得:,由图象可得,,故此选项错误;
、当时,随的增大而增大,故此选项错误;
故选:.
【点评】此题主要考查了二次函数图象与系数的关系,关键是从抛物线中的得到正确信息.
①二次项系数决定抛物线的开口方向和大小.
当时,抛物线向上开口;当时,抛物线向下开口;还可以决定开口大小,越大开口就越小.
②一次项系数和二次项系数共同决定对称轴的位置.
当与同号时即,对称轴在轴左; 当与异号时即,对称轴在轴右.简称:左同右异
③常数项决定抛物线与轴交点. 抛物线与轴交于,.
④抛物线与轴交点个数.时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.
5. 【答案】C
【解析】A.由抛物线可知,,得 ,由直线可知,,,故本选项错误;
B.由抛物线可知,,,由直线可知,,,故本选项错误;
C.由抛物线可知,,,由直线可知,,,且交 轴同一点,故本选项正确;
D.由抛物线可知,,,由直线可知,, 故本选项错误.
6. 【答案】D
【解析】当抛物线 的顶点在线段 的 点上时,点 的横坐标最小,
把 代入得:,
把 代入得:,解得:,
即:,
抛物线 的顶点在线段 上运动,
抛物线的 永远等于 ,
当抛物线的顶点运动到 时, 的横坐标最大,
把 和顶点 代入 得:,
当 时,,解得 或 (不合题意,舍去).
点 的横坐标最大值为 .
7. 【答案】D
【解析】令 ,即 ,解得 ,
则点 ,,
由于将 向右平移 个长度单位得 ,
则 解析式为 ,
当 与 相切时,
联立
即 ,,
解得 ,
当 过点 时,即 ,,
当 时直线 与 , 共有 个不同的交点.
8. 【答案】B
【解析】 函数 与 轴无交点,
,
故①错误;
当 时,,则 .
故②正确;
根据抛物线开口向上,对称轴为直线 ,
当 时, 随 的增大而减小,
图象上两点 , 满足 ,
故③正确;
当 时,二次函数值小于一次函数值,
,
,
故④正确.
二、填空题(共8题)
9. 【答案】
【解析】根据题意可知 ,,
故二次函数解析式可以是 .
10. 【答案】
【解析】由于二次函数 的图象经过原点,
把 代入 ,得:,
解得:.
11. 【答案】
【解析】 是方程 的根,
,
当 时,函数 ().
12. 【答案】
【解析】设抛物线解析式为 ,
把点 代入解析式得:,
解得:,
,
把 代入,得:,
此时水深 (米).
13. 【答案】 或
【解析】 抛物线 与直线 相交于点 ,点 ,
方程 的解为: 或 ,
根据图象可知:不等式 的解集为: 或 .
14. 【答案】
【解析】 ,
,
时,.
15. 【答案】
【解析】 ,
二次函数 与 轴两个交点坐标为 ,,
则直线 与抛物线 的交点的横坐标分别为 与 ,
所以 .
故答案为 .
16. 【答案】
【解析】如图.
,
平移后抛物线的顶点坐标为 ,对称轴为直线 ,
在 中,当 时,,
平移后阴影部分的面积等于如图三角形的面积,.
三、解答题(共6题)
17. 【答案】将 ,, 代入解析式得,
解得
抛物线的解析式为:,顶点坐标为 .
18. 【答案】
(1) 由题意 ,解得 ,
当 时,,不合题意;
的值为 .
(2) 由题意 .
,
,
当 时,.
的最大值为 .
19. 【答案】
(1) 该二次函数图象与 轴有 个交点.
,
,
该二次函数图象与 轴有 个交点.
(2) 该二次函数的顶点坐标为 ,
,,
,.
(3) ,
抛物线 的顶点坐标为 ,
把抛物线 向上平移 个单位后顶点坐标为 ,
把函数图象向上平移 个单位,使得对于任意的 都有 大于 ,
平移后的抛物线在 轴上方,
,
.
20. 【答案】
(1) 根据题意得:
(2) 令 中 ,则有:,
即 ,
解得:(舍去),.
所以若要平均每天盈利 元,则每千克应降价 元.
(3) ,
所以每千克降价 元时,每天的盈利最多,最多盈利多, 元.
21. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得: 解得:
与 的函数解析式为 .
(2) .
,
当 时, 随 的增大而增大.
当 时, 最大,最大利润为 元.
当销售价为 元时,每天的销售利润最大,最大利润为 元.
22. 【答案】
(1) 点 在直线 上,
,
,
把 ,, 三点坐标代入抛物线解析式,
可得 解得
抛物线解析式为 .
(2) 设 ,则 ,,
则 ,,
,
,
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
;
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
.
综上可知, 点坐标为 或 .
(3) 存在这样的点 ,使得四边形 的面积最大.
如图,过点 作 轴于点 ,
设 ,
则 ,,,
当 时,四边形 的面积取得最大值,最大值为 ,
此时点 的坐标为 .
一、选择题
由二次函数 可知
A.其图象的开口向下
B.其图象的对称轴为直线
C.其顶点坐标为
D.当 时, 随 的增大而增大
抛物线 与坐标轴的交点个数是
A. B. C. D.
若抛物线 经过点 ,则 的值是
A. B. C. D.
已知二次函数的图象如图所示,则下列结论中正确的是
A. B.3是方程的一个根
C. D.当时,随的增大而减小
在同一平面直角坐标系内,一次函数 与二次函数 的图象可能是
A. B. C. D.
如图,点 , 的坐标分别为 和 ,抛物线 的顶点在线段 上运动,与 轴交于 , 两点( 在 的左侧),点 的横坐标最小值为 ,则点 的横坐标最大值为
A. B. C. D.
如图,抛物线 与 轴交于点 ,,把抛物线在 轴及其上方的部分记作 ,将 向右平移得 , 与 轴交于点 ,.若直线 与 , 共有 个不同的交点,则 的取值范围是
A. B.
C. D.
函数 与 的图象如图所示,以下结论:① ,② ,③若图象上两点 , 满足 ,则 ,④当 时, 其中正确的有 个.
A. B. C. D.
二、填空题
请你写出一个二次函数,其图象满足条件:①开口向下;②与 轴的交点坐标为 .此二次函数的解析式可以是 .
若二次函数 的图象经过原点,则 .
若 是方程 的根,当 时,函数 的函数值为 .
有一座抛物线形拱桥,正常水位时桥下水面宽度为 米,拱顶距离水面 米.设正常水位时桥下的水深为 米,为保证过往船只顺利航行,桥下水面的宽度不得小于 米,则水深超过 米时就会影响过往船只在桥下的顺利航行.
如图,抛物线 与直线 相交于点 ,点 ,则关于 的不等式 的解集为 .
烟花厂为咸宁温泉旅游节特别设计制作一种新型礼炮,这种礼炮的升空高 与飞行时间 的关系式是 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要时间为 .
若 , 是关于 的方程 的两根,且 ,则 ,,, 的大小关系是 .
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为 .
三、解答题
已知抛物线 经过点 ,,.求此抛物线的函数解析式和顶点坐标.
如图,某公司要建一个矩形的产品展示台,展示台的一边靠长为 的宣传版(这条边不能超出宣传版),另三边用总长为 的红布粘贴在展示台边上.设垂直于宣传版的一边长为 .
(1) 当展示台的面积为 时,求 的值;
(2) 设展示台的面积为 ,求 的最大值.
已知二次函数 .
(1) 判断该二次函数图象与 轴交点的个数,并说明理由.
(2) 若该二次函数的顶点坐标为 ,求 , 的值.
(3) 若把该函数图象向上平移 个单位,使得对于任意的 都有 大于 ,求征:.
某商店原来平均每天可销售某种水果 千克,每千克可盈利 元,为减少库存,经市场调查,如果这种水果每千克降价 元,则每天可所多售出 千克.
(1) 设每千克水果降价 元,平均每天盈利 元,试写出 关于 的函数表达式;
(2) 若要平均每天盈利 元,则每千克应降价多少元?
(3) 每千克降价多少元时,每天的盈利最多?最多盈利多少元?
一名大学生利用“互联网 ”自主创业,销售一种产品,这种产品的成本价为 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 元/件,市场调查发现,该产品每天的销售量 (件)与 (元/件)之间的函数关系如图所示.
(1) 求 与 之间的函数关系式,并写出自变量 的取值范围;
(2) 求每天的销售利润 (元)与销售单价 (元/件)之间的函数关系式,并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
如图 ,抛物线 与直线 相交于 , 两点,且抛物线经过点 .
(1) 求抛物线的解析式.
(2) 点 是抛物线上的一个动点(不与点 点 重合),过点 作直线 轴于点 ,交直线 于点 .当 时,求 点坐标.
(3) 如图 所示,设抛物线与 轴交于点 ,在抛物线的第一象限内,是否存在一点 ,使得四边形 的面积最大?若存在,请求出点 的坐标;若不存在,说明理由.
答案
一、选择题(共8题)
1. 【答案】B
【解析】 ,
抛物线开口向上,故A不正确;
对称轴为 ,故B正确;
当 时, 有最小值 ,故C不正确;
当 时, 随 的增大而增大,故D不正确.
2. 【答案】C
【解析】令 ,则 ,
,
二次函数 的图象与 轴有 个交点,
抛物线 与 轴有 个交点,
抛物线 与坐标轴的交点的个数是 .
3. 【答案】B
【解析】 抛物线 经过点
代入,得 ,
,
.
4. 【答案】B
【解析】【分析】根据抛物线的开口方向可得,根据抛物线对称轴可得方程的根为,;根据图象可得时,;根据抛物线可直接得到时,随的增大而增大.
【解析】解:、因为抛物线开口向下,因此,故此选项错误;
、根据对称轴为,一个交点坐标为,可得另一个与轴的交点坐标为,因此3是方程的一个根,故此选项正确;
、把代入二次函数中得:,由图象可得,,故此选项错误;
、当时,随的增大而增大,故此选项错误;
故选:.
【点评】此题主要考查了二次函数图象与系数的关系,关键是从抛物线中的得到正确信息.
①二次项系数决定抛物线的开口方向和大小.
当时,抛物线向上开口;当时,抛物线向下开口;还可以决定开口大小,越大开口就越小.
②一次项系数和二次项系数共同决定对称轴的位置.
当与同号时即,对称轴在轴左; 当与异号时即,对称轴在轴右.简称:左同右异
③常数项决定抛物线与轴交点. 抛物线与轴交于,.
④抛物线与轴交点个数.时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.
5. 【答案】C
【解析】A.由抛物线可知,,得 ,由直线可知,,,故本选项错误;
B.由抛物线可知,,,由直线可知,,,故本选项错误;
C.由抛物线可知,,,由直线可知,,,且交 轴同一点,故本选项正确;
D.由抛物线可知,,,由直线可知,, 故本选项错误.
6. 【答案】D
【解析】当抛物线 的顶点在线段 的 点上时,点 的横坐标最小,
把 代入得:,
把 代入得:,解得:,
即:,
抛物线 的顶点在线段 上运动,
抛物线的 永远等于 ,
当抛物线的顶点运动到 时, 的横坐标最大,
把 和顶点 代入 得:,
当 时,,解得 或 (不合题意,舍去).
点 的横坐标最大值为 .
7. 【答案】D
【解析】令 ,即 ,解得 ,
则点 ,,
由于将 向右平移 个长度单位得 ,
则 解析式为 ,
当 与 相切时,
联立
即 ,,
解得 ,
当 过点 时,即 ,,
当 时直线 与 , 共有 个不同的交点.
8. 【答案】B
【解析】 函数 与 轴无交点,
,
故①错误;
当 时,,则 .
故②正确;
根据抛物线开口向上,对称轴为直线 ,
当 时, 随 的增大而减小,
图象上两点 , 满足 ,
故③正确;
当 时,二次函数值小于一次函数值,
,
,
故④正确.
二、填空题(共8题)
9. 【答案】
【解析】根据题意可知 ,,
故二次函数解析式可以是 .
10. 【答案】
【解析】由于二次函数 的图象经过原点,
把 代入 ,得:,
解得:.
11. 【答案】
【解析】 是方程 的根,
,
当 时,函数 ().
12. 【答案】
【解析】设抛物线解析式为 ,
把点 代入解析式得:,
解得:,
,
把 代入,得:,
此时水深 (米).
13. 【答案】 或
【解析】 抛物线 与直线 相交于点 ,点 ,
方程 的解为: 或 ,
根据图象可知:不等式 的解集为: 或 .
14. 【答案】
【解析】 ,
,
时,.
15. 【答案】
【解析】 ,
二次函数 与 轴两个交点坐标为 ,,
则直线 与抛物线 的交点的横坐标分别为 与 ,
所以 .
故答案为 .
16. 【答案】
【解析】如图.
,
平移后抛物线的顶点坐标为 ,对称轴为直线 ,
在 中,当 时,,
平移后阴影部分的面积等于如图三角形的面积,.
三、解答题(共6题)
17. 【答案】将 ,, 代入解析式得,
解得
抛物线的解析式为:,顶点坐标为 .
18. 【答案】
(1) 由题意 ,解得 ,
当 时,,不合题意;
的值为 .
(2) 由题意 .
,
,
当 时,.
的最大值为 .
19. 【答案】
(1) 该二次函数图象与 轴有 个交点.
,
,
该二次函数图象与 轴有 个交点.
(2) 该二次函数的顶点坐标为 ,
,,
,.
(3) ,
抛物线 的顶点坐标为 ,
把抛物线 向上平移 个单位后顶点坐标为 ,
把函数图象向上平移 个单位,使得对于任意的 都有 大于 ,
平移后的抛物线在 轴上方,
,
.
20. 【答案】
(1) 根据题意得:
(2) 令 中 ,则有:,
即 ,
解得:(舍去),.
所以若要平均每天盈利 元,则每千克应降价 元.
(3) ,
所以每千克降价 元时,每天的盈利最多,最多盈利多, 元.
21. 【答案】
(1) 设 与 的函数解析式为 ,
由题意得: 解得:
与 的函数解析式为 .
(2) .
,
当 时, 随 的增大而增大.
当 时, 最大,最大利润为 元.
当销售价为 元时,每天的销售利润最大,最大利润为 元.
22. 【答案】
(1) 点 在直线 上,
,
,
把 ,, 三点坐标代入抛物线解析式,
可得 解得
抛物线解析式为 .
(2) 设 ,则 ,,
则 ,,
,
,
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
;
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
.
综上可知, 点坐标为 或 .
(3) 存在这样的点 ,使得四边形 的面积最大.
如图,过点 作 轴于点 ,
设 ,
则 ,,,
当 时,四边形 的面积取得最大值,最大值为 ,
此时点 的坐标为 .
同课章节目录
