2024-2025学年山东省淄博市博山一中八年级(上)期中数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市博山一中八年级(上)期中数学试卷(五四学制)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览




文档简介
2024-2025学年山东省淄博市博山一中八年级(上)期中数学试卷(五四学制)
一、选择题
1.(3分)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
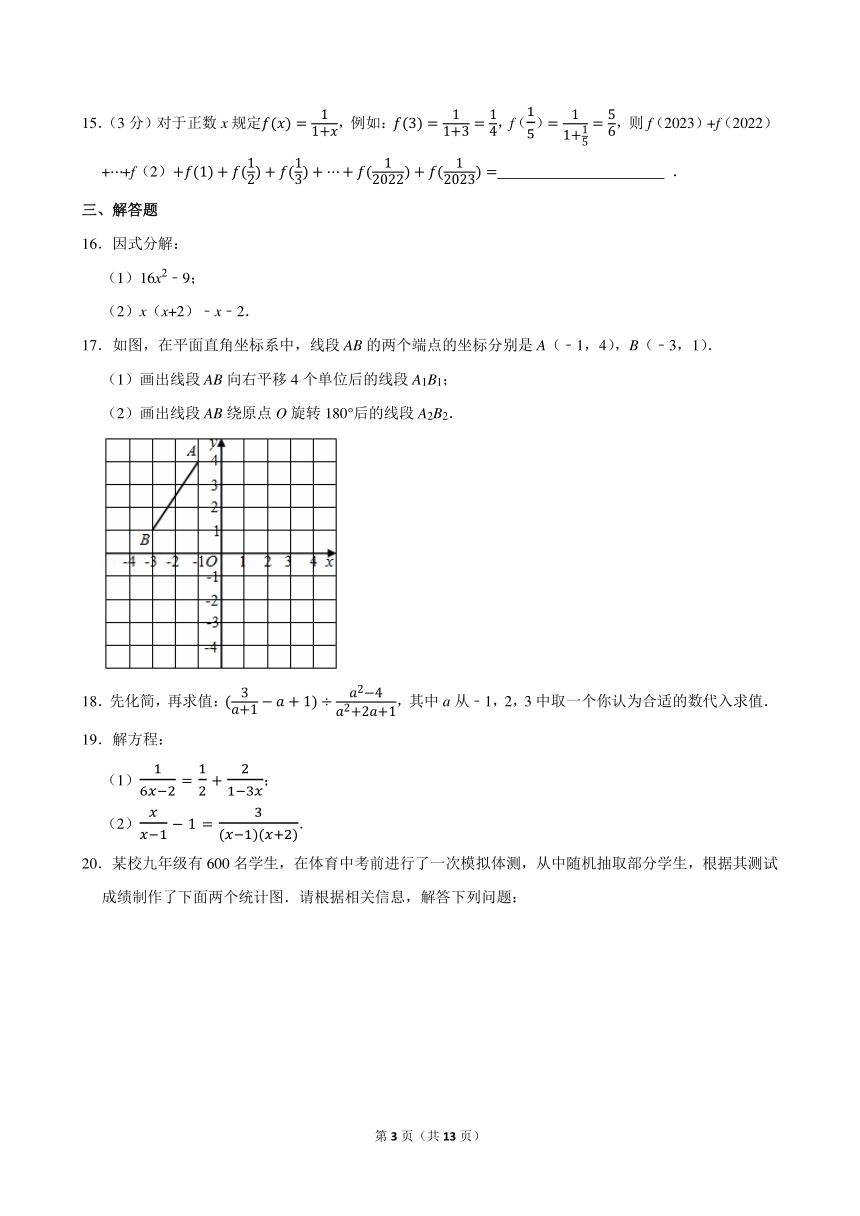
2.(3分)若分式有意义,则x满足的条件是( )
A.x≠3 B.x>3 C.x≠0 D.x<3
3.(3分)若分式中a、b的值同时扩大到原来的2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.扩大6倍
4.(3分)根据分式的基本性质,分式可变形为( )
A. B. C. D.
5.(3分)九年一班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次为100分、90分、80分、70分,该班竞赛成绩的统计图如图所示,以下说法正确的是( )
A.B等级人数比A等级人数少21人
B.50人得分的众数是80分
C.50人得分的平均数是80分
D.50人得分的中位数是80分
6.(3分)若关于x的分式方程1有增根,则a的值为( )
A.﹣3 B.3 C.2 D.
7.(3分)下列各式:①;②;③;④;⑤,最简分式有( )
A.2个 B.3个 C.4个 D.5个
8.(3分)若4x2﹣(k﹣1)x+9能用完全平方公式因式分解,则k的值是( )
A.13 B.13或﹣11 C.﹣11 D.无法确定
9.(3分)已知实数a,b,c满足a+b+c=10,且,则的值是( )
A. B. C.2 D.
10.(3分)在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )
A.②③④ B.①③④ C.①②④ D.①②③
二、填空题
11.(3分)分解因式:36x2﹣4= .
12.(3分)关于x的方程2的解为正数,则a的取值范围为 .
13.(3分)如图,在三角形ABC中,∠ABC=90°,将三角形ABC沿BC方向平移得到三角形DEF,其中AB=7,BE=3,DM=2,则阴影部分的面积是 .
14.(3分)若一组数据x1,x2,x3, ,xn的方差为2,则数据x1+3,x2+3,x3+3, ,xn+3的方差是 .
15.(3分)对于正数x规定,例如:,f(),则f(2023)+f(2022)+ +f(2) .
三、解答题
16.因式分解:
(1)16x2﹣9;
(2)x(x+2)﹣x﹣2.
17.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(﹣1,4),B(﹣3,1).
(1)画出线段AB向右平移4个单位后的线段A1B1;
(2)画出线段AB绕原点O旋转180°后的线段A2B2.
18.先化简,再求值:,其中a从﹣1,2,3中取一个你认为合适的数代入求值.
19.解方程:
(1);
(2).
20.某校九年级有600名学生,在体育中考前进行了一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
(Ⅰ)本次被抽取到的学生人数为 ,图1中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
21.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传生物多样性,某校组织七、八年级各200名学生对《生物多样性公约》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】
七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
年级 统计量 平均数 中位数 众数 方差
七年级 80 b 72 66.6
八年级 80 80 c s八年级2
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差,并估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(至少写出两条理由).
22.观察下列方程的特征及其解的特点;
①x3的解为x1=﹣1,x2=﹣2.
②x5的解为x1=﹣2,x2=﹣3.
③x7的解为x1=﹣3,x2=﹣4;
解答下列问题;
(1)请你写出一个符合上述特征的方程为 ,其解为 .
(2)根据这类方程特征,写出第n个方程为 ,其解为 .
(3)请利用(2)的结论,求关于x的方程x2(n+2)(其中n为正整数)的解.
23.2022年10月16日,习总书记在第二十次全国代表大会上的报告中提出:“积极稳妥推进碳达峰碳中和”.某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用3000万元购进A型汽车的数量比2400万元购进B型汽车的数量少20辆.
(1)A型和B型汽车的进价分别为每辆多少万元?
(2)该公司决定用不多于3600万元购进A型和B型汽车共150辆,最多可以购买多少辆A型汽车?
2024-2025学年山东省淄博市博山一中八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C D D A A B A D
一、选择题
1.解:只有D的图形的形状和大小没有变化,符合平移的性质,属于平移得到;
故选:D.
2.解:∵分式有意义,
∴x﹣3≠0,解得x≠3.
故选:A.
3.解:把分式中a、b的值同时扩大到原来的2倍,得到的新分式为,
∴分式的值扩大了4倍,
故选:C.
4.解:A.∵,
∴,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项不符合题意;
D.,故本选项符合题意;
故选:D.
5.解:A、B等级人数比A等级人数少50×(44%﹣4%)=20(人),故此选项不符合题意;
B、50人得分的众数是100分,故此选项不符合题意;
C、50人得分的平均数是100×44%+90×4%+80×36%+70×16%=87.6(分),故此选项不符合题意;
D、50人得分的中位数是80分,故此选项符合题意.
故选:D.
6.解:方程两边都乘以(x﹣2)得:6﹣(x﹣2)=﹣ax,
解得:x,
∵方程有增根,
∴x﹣2=0,
∴x=2,
∴2,
解得:a=﹣3.
故选:A.
7.解:①,因此①是最简分式;
②,因此②不是最简分式;
③,因此③不是最简分式;
④是整式,不是分式;
⑤是最简分式;
综上所述,①⑤是最简分式,有2个,
故选:A.
8.解:∵4x2﹣(k﹣1)x+9能用完全平方公式因式分解,4x2﹣(k﹣1)x+9=(2x)2﹣(k﹣1)x+32,
∴k﹣1=±2×2×3,
解得:k=13或﹣11,
故选:B.
9.解:∵a+b+c=10,,
∴a=10﹣(b+c),b=10﹣(a+c),c=10﹣(a+b),
∴
=10()﹣3
=103
.
故选:A.
10.解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以③正确.
故选:D.
二、填空题
11.解:36x2﹣4
=4(9x2﹣1)
=4(3x+1)(3x﹣1).
故答案为:4(3x+1)(3x﹣1).
12.解:去分母,得2﹣(5﹣a)=﹣2(x﹣1),
去括号,得2﹣5+a=﹣2x+2,
整理,得2x=5﹣a,
∴x.
若方程的解为正数,则0且1.
∴a<5且a≠3.
13.解:如图,连接AD,由平移的性质可知,AD=BE=CF=3,
S阴影部分=S平行四边形ACFD﹣S△ADM
=3×72×3
=18,
故答案为:18.
14.解:∵数据x1,x2,x3, ,xn的方差是2,
∴数据x1+3,x2+3,x3+3, ,xn+3的波动幅度不变,
∴数据x1+3,x2+3,x3+3, ,xn+3的方差为2,
故答案为:2.
15.解:由题意可得:f(1),f(3),f(),f(5),f(),
则f(x)+f()=1,
原式=[f(2023)+f()]+[f(2022)+f()]+…+[f(2)+f()]+f(1)
=1+1+…+1
=1×(2023﹣1)
=2022,
故答案为:2022.
三、解答题
16.解:(1)原式=(4x)2﹣32
=(4x+3)(4x﹣3).
(2)原式=x(x+2)﹣(x+2)
=(x+2)(x﹣1).
17.解:(1)如图,线段A1B1即为所求.
(2)如图,线段A2B2即为所求.
18.解:
=﹣a﹣1,
根据分式有意义的条件知a≠﹣1且a≠2,
则a=3,
原式=﹣3﹣1=﹣4.
19.解:(1)原分式方程整理得,
1=3x﹣1﹣4,
3x=6,
x=2,
检验,当x=2时,2(3x﹣1)=2(3×2﹣1)=10≠0,
所以该分式方程的解为:x=2;
(2)原分式方程去分母得x(x+2)﹣(x﹣1)(x+2)=3,
x2+2x﹣x2﹣x+2=3,
x=1,
检验,当x=1时,(x﹣1)(x+2)=(1﹣1)(1+2)=0,
所以该分式方程无解.
20.解:(Ⅰ)本次被抽取到的学生人数为4÷8%=50(人),m%100%=28%,即m=28,
故答案为:50人、28;
(Ⅱ)∵,
∴本次调查获取的样本数据的平均数是10.66.
∵在这组样本数据中,12出现了16次,出现的次数最多,
∴这组样本数据的众数是12.
∵将这组样本数据按照有小到大的顺序排列,其中处于中间位置的两个数都是11,有,
∴这组样本数据的中位数是11.
(Ⅲ)∵在50名学生中,模拟体测得12分的学生人数比例为32%,
∴由样本数据,估计该校九年级体测测试中得12分的学生人数比例约为32%,
∴600×32%=192(人)
答:估计该校九年级模拟体测中得12分的学生约有192人.
21.解:(1)将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位为b(分),
将八年级的成绩出现次数最多是8(0分),共出现2次,
∴众数c=80(分),
故答案为:2,78.5,80;
(2)(80﹣80)2+(80﹣76)2+(80﹣82)2]=33.
∵七年级同学测试成绩的方差是66.6,八年级同学测试成绩的方差是33,
∴,
∴估计八年级学生的竞赛成绩更整齐些.
(3)由题意得(人),
∴这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,八年级的中位数高于七年级;八年级的众数高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
22.解:(1)x,其解为:x1=﹣4,x2=﹣5,
经检验:x1=﹣4,x2=﹣5是原方程的解,
故答案为:x9,x1=﹣4,x2=﹣5;
(2)x(2n+1),其解为:x1=﹣n,x2=﹣n﹣1,
故答案为:x(2n+1),x1=﹣n,x2=﹣n﹣1;
(3)x2(n+2)
x+32(n+2)+3
(x+3)(2n+1)
∴x+3=﹣n或x+3=﹣(n+1),
即:x1=﹣n﹣3,x2=﹣n﹣4.
经检验:x1=﹣n﹣3,x2=﹣n﹣4是原方程的解,
23.解:(1)设B型汽车的进价为每辆x万元,则A型汽车的进价为每辆1.5x万元,
依题意得:,
解得:x=20,
经检验,x=20是方程的解,且符合题意,
则1.5x=1.5×20=30,
答:A型汽车的进价为每辆30万元,B型汽车的进价为每辆20万元;
(2)设购买辆A型汽车m辆,则购买(150﹣m)辆B型汽车,
依题意得:30m+20(150﹣m)≤3600,
解得:m≤60,
答:最多可以购买60辆A型汽车.
第1页(共1页)
一、选择题
1.(3分)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
2.(3分)若分式有意义,则x满足的条件是( )
A.x≠3 B.x>3 C.x≠0 D.x<3
3.(3分)若分式中a、b的值同时扩大到原来的2倍,则分式的值( )
A.不变 B.扩大2倍 C.扩大4倍 D.扩大6倍
4.(3分)根据分式的基本性质,分式可变形为( )
A. B. C. D.
5.(3分)九年一班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次为100分、90分、80分、70分,该班竞赛成绩的统计图如图所示,以下说法正确的是( )
A.B等级人数比A等级人数少21人
B.50人得分的众数是80分
C.50人得分的平均数是80分
D.50人得分的中位数是80分
6.(3分)若关于x的分式方程1有增根,则a的值为( )
A.﹣3 B.3 C.2 D.
7.(3分)下列各式:①;②;③;④;⑤,最简分式有( )
A.2个 B.3个 C.4个 D.5个
8.(3分)若4x2﹣(k﹣1)x+9能用完全平方公式因式分解,则k的值是( )
A.13 B.13或﹣11 C.﹣11 D.无法确定
9.(3分)已知实数a,b,c满足a+b+c=10,且,则的值是( )
A. B. C.2 D.
10.(3分)在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC.其中正确的序号是( )
A.②③④ B.①③④ C.①②④ D.①②③
二、填空题
11.(3分)分解因式:36x2﹣4= .
12.(3分)关于x的方程2的解为正数,则a的取值范围为 .
13.(3分)如图,在三角形ABC中,∠ABC=90°,将三角形ABC沿BC方向平移得到三角形DEF,其中AB=7,BE=3,DM=2,则阴影部分的面积是 .
14.(3分)若一组数据x1,x2,x3, ,xn的方差为2,则数据x1+3,x2+3,x3+3, ,xn+3的方差是 .
15.(3分)对于正数x规定,例如:,f(),则f(2023)+f(2022)+ +f(2) .
三、解答题
16.因式分解:
(1)16x2﹣9;
(2)x(x+2)﹣x﹣2.
17.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(﹣1,4),B(﹣3,1).
(1)画出线段AB向右平移4个单位后的线段A1B1;
(2)画出线段AB绕原点O旋转180°后的线段A2B2.
18.先化简,再求值:,其中a从﹣1,2,3中取一个你认为合适的数代入求值.
19.解方程:
(1);
(2).
20.某校九年级有600名学生,在体育中考前进行了一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
(Ⅰ)本次被抽取到的学生人数为 ,图1中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
21.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传生物多样性,某校组织七、八年级各200名学生对《生物多样性公约》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】
七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
年级 统计量 平均数 中位数 众数 方差
七年级 80 b 72 66.6
八年级 80 80 c s八年级2
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差,并估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(至少写出两条理由).
22.观察下列方程的特征及其解的特点;
①x3的解为x1=﹣1,x2=﹣2.
②x5的解为x1=﹣2,x2=﹣3.
③x7的解为x1=﹣3,x2=﹣4;
解答下列问题;
(1)请你写出一个符合上述特征的方程为 ,其解为 .
(2)根据这类方程特征,写出第n个方程为 ,其解为 .
(3)请利用(2)的结论,求关于x的方程x2(n+2)(其中n为正整数)的解.
23.2022年10月16日,习总书记在第二十次全国代表大会上的报告中提出:“积极稳妥推进碳达峰碳中和”.某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用3000万元购进A型汽车的数量比2400万元购进B型汽车的数量少20辆.
(1)A型和B型汽车的进价分别为每辆多少万元?
(2)该公司决定用不多于3600万元购进A型和B型汽车共150辆,最多可以购买多少辆A型汽车?
2024-2025学年山东省淄博市博山一中八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C D D A A B A D
一、选择题
1.解:只有D的图形的形状和大小没有变化,符合平移的性质,属于平移得到;
故选:D.
2.解:∵分式有意义,
∴x﹣3≠0,解得x≠3.
故选:A.
3.解:把分式中a、b的值同时扩大到原来的2倍,得到的新分式为,
∴分式的值扩大了4倍,
故选:C.
4.解:A.∵,
∴,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项不符合题意;
D.,故本选项符合题意;
故选:D.
5.解:A、B等级人数比A等级人数少50×(44%﹣4%)=20(人),故此选项不符合题意;
B、50人得分的众数是100分,故此选项不符合题意;
C、50人得分的平均数是100×44%+90×4%+80×36%+70×16%=87.6(分),故此选项不符合题意;
D、50人得分的中位数是80分,故此选项符合题意.
故选:D.
6.解:方程两边都乘以(x﹣2)得:6﹣(x﹣2)=﹣ax,
解得:x,
∵方程有增根,
∴x﹣2=0,
∴x=2,
∴2,
解得:a=﹣3.
故选:A.
7.解:①,因此①是最简分式;
②,因此②不是最简分式;
③,因此③不是最简分式;
④是整式,不是分式;
⑤是最简分式;
综上所述,①⑤是最简分式,有2个,
故选:A.
8.解:∵4x2﹣(k﹣1)x+9能用完全平方公式因式分解,4x2﹣(k﹣1)x+9=(2x)2﹣(k﹣1)x+32,
∴k﹣1=±2×2×3,
解得:k=13或﹣11,
故选:B.
9.解:∵a+b+c=10,,
∴a=10﹣(b+c),b=10﹣(a+c),c=10﹣(a+b),
∴
=10()﹣3
=103
.
故选:A.
10.解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以③正确.
故选:D.
二、填空题
11.解:36x2﹣4
=4(9x2﹣1)
=4(3x+1)(3x﹣1).
故答案为:4(3x+1)(3x﹣1).
12.解:去分母,得2﹣(5﹣a)=﹣2(x﹣1),
去括号,得2﹣5+a=﹣2x+2,
整理,得2x=5﹣a,
∴x.
若方程的解为正数,则0且1.
∴a<5且a≠3.
13.解:如图,连接AD,由平移的性质可知,AD=BE=CF=3,
S阴影部分=S平行四边形ACFD﹣S△ADM
=3×72×3
=18,
故答案为:18.
14.解:∵数据x1,x2,x3, ,xn的方差是2,
∴数据x1+3,x2+3,x3+3, ,xn+3的波动幅度不变,
∴数据x1+3,x2+3,x3+3, ,xn+3的方差为2,
故答案为:2.
15.解:由题意可得:f(1),f(3),f(),f(5),f(),
则f(x)+f()=1,
原式=[f(2023)+f()]+[f(2022)+f()]+…+[f(2)+f()]+f(1)
=1+1+…+1
=1×(2023﹣1)
=2022,
故答案为:2022.
三、解答题
16.解:(1)原式=(4x)2﹣32
=(4x+3)(4x﹣3).
(2)原式=x(x+2)﹣(x+2)
=(x+2)(x﹣1).
17.解:(1)如图,线段A1B1即为所求.
(2)如图,线段A2B2即为所求.
18.解:
=﹣a﹣1,
根据分式有意义的条件知a≠﹣1且a≠2,
则a=3,
原式=﹣3﹣1=﹣4.
19.解:(1)原分式方程整理得,
1=3x﹣1﹣4,
3x=6,
x=2,
检验,当x=2时,2(3x﹣1)=2(3×2﹣1)=10≠0,
所以该分式方程的解为:x=2;
(2)原分式方程去分母得x(x+2)﹣(x﹣1)(x+2)=3,
x2+2x﹣x2﹣x+2=3,
x=1,
检验,当x=1时,(x﹣1)(x+2)=(1﹣1)(1+2)=0,
所以该分式方程无解.
20.解:(Ⅰ)本次被抽取到的学生人数为4÷8%=50(人),m%100%=28%,即m=28,
故答案为:50人、28;
(Ⅱ)∵,
∴本次调查获取的样本数据的平均数是10.66.
∵在这组样本数据中,12出现了16次,出现的次数最多,
∴这组样本数据的众数是12.
∵将这组样本数据按照有小到大的顺序排列,其中处于中间位置的两个数都是11,有,
∴这组样本数据的中位数是11.
(Ⅲ)∵在50名学生中,模拟体测得12分的学生人数比例为32%,
∴由样本数据,估计该校九年级体测测试中得12分的学生人数比例约为32%,
∴600×32%=192(人)
答:估计该校九年级模拟体测中得12分的学生约有192人.
21.解:(1)将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位为b(分),
将八年级的成绩出现次数最多是8(0分),共出现2次,
∴众数c=80(分),
故答案为:2,78.5,80;
(2)(80﹣80)2+(80﹣76)2+(80﹣82)2]=33.
∵七年级同学测试成绩的方差是66.6,八年级同学测试成绩的方差是33,
∴,
∴估计八年级学生的竞赛成绩更整齐些.
(3)由题意得(人),
∴这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,八年级的中位数高于七年级;八年级的众数高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
22.解:(1)x,其解为:x1=﹣4,x2=﹣5,
经检验:x1=﹣4,x2=﹣5是原方程的解,
故答案为:x9,x1=﹣4,x2=﹣5;
(2)x(2n+1),其解为:x1=﹣n,x2=﹣n﹣1,
故答案为:x(2n+1),x1=﹣n,x2=﹣n﹣1;
(3)x2(n+2)
x+32(n+2)+3
(x+3)(2n+1)
∴x+3=﹣n或x+3=﹣(n+1),
即:x1=﹣n﹣3,x2=﹣n﹣4.
经检验:x1=﹣n﹣3,x2=﹣n﹣4是原方程的解,
23.解:(1)设B型汽车的进价为每辆x万元,则A型汽车的进价为每辆1.5x万元,
依题意得:,
解得:x=20,
经检验,x=20是方程的解,且符合题意,
则1.5x=1.5×20=30,
答:A型汽车的进价为每辆30万元,B型汽车的进价为每辆20万元;
(2)设购买辆A型汽车m辆,则购买(150﹣m)辆B型汽车,
依题意得:30m+20(150﹣m)≤3600,
解得:m≤60,
答:最多可以购买60辆A型汽车.
第1页(共1页)
同课章节目录
