2024-2025学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 605.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 00:00:00 | ||
图片预览



文档简介
2024-2025学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.(4分)下列图形既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(4分)分式有意义,则x的取值范围是( )
A.x>2 B.x=2 C.x≠2 D.x<2
3.(4分)将多项式x2+6x﹣16因式分解,正确的是( )
A.(x﹣2)(x+8) B.(x+2)(x﹣8)
C.(x+4)(x﹣4) D.(x﹣4)2
4.(4分)如果a+b=3,ab=1,那么a3b+2a2b2+ab3的值为( )
A.0 B.1 C.4 D.9
5.(4分)在平面直角坐标系中,将点P(4,3)向右平移2个单位长度,再向下平移2个单位长度所得到的点的坐标为( )
A.(2,1) B.(2,3) C.(6,5) D.(6,1)
6.(4分)为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表:
月用电量(度) 25 30 40 50 60
户数 1 2 4 2 1
关于这10户家庭的月用电量说法正确的是( )
A.中位数是40 B.众数是4
C.平均数是20.5 D.极差是3
7.(4分)分式方程1的解为正数,则m的取值范围( )
A.m>﹣3 B.m>﹣3且m≠﹣2
C.m<3 D.m<3且m≠﹣2
8.(4分)某市工程队要修路1000米,因天气原因,实施施工时“…”,设原计划平均每天修x米,则可得方程5,根据此情景,题中用“…”表示的缺失的条件应为( )
A.每天比原计划多铺设10米,结果延期5天才完成
B.每天比原计划少铺设10米,结果延期5天才完成
C.每天比原计划多铺设10米,结果提前5天完成了
D.每天比原计划少铺设10米,结果提前5天完成了
9.(4分)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
10.(4分)如图,在等边三角形ABC中,有一点P,连接PA、PB、PC,将BP绕点B逆时针旋转60°得到BD,连接PD、AD,有如下结论:①△BPC≌△BDA;②△BDP是等边三角形;③如果∠BPC=150°,那么PA2=PB2+PC2.以上结论正确的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.(4分)如果分式的值为零,那么x的值为 .
12.(4分)在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是 .
13.(4分)已知一组数据为1,2,3,4,5,则这组数据的方差为 .
14.(4分)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD的大小为 度.
15.(4分)已知a1=x+1(x≠0且x≠﹣1),,,…,,则a2025的值为 .
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共90分)
16.分解因式:
(1)2x2﹣8
(2)(x+2)(x+4)+1
17.计算:
(1)
(2)
18.解方程:
(1)
(2)
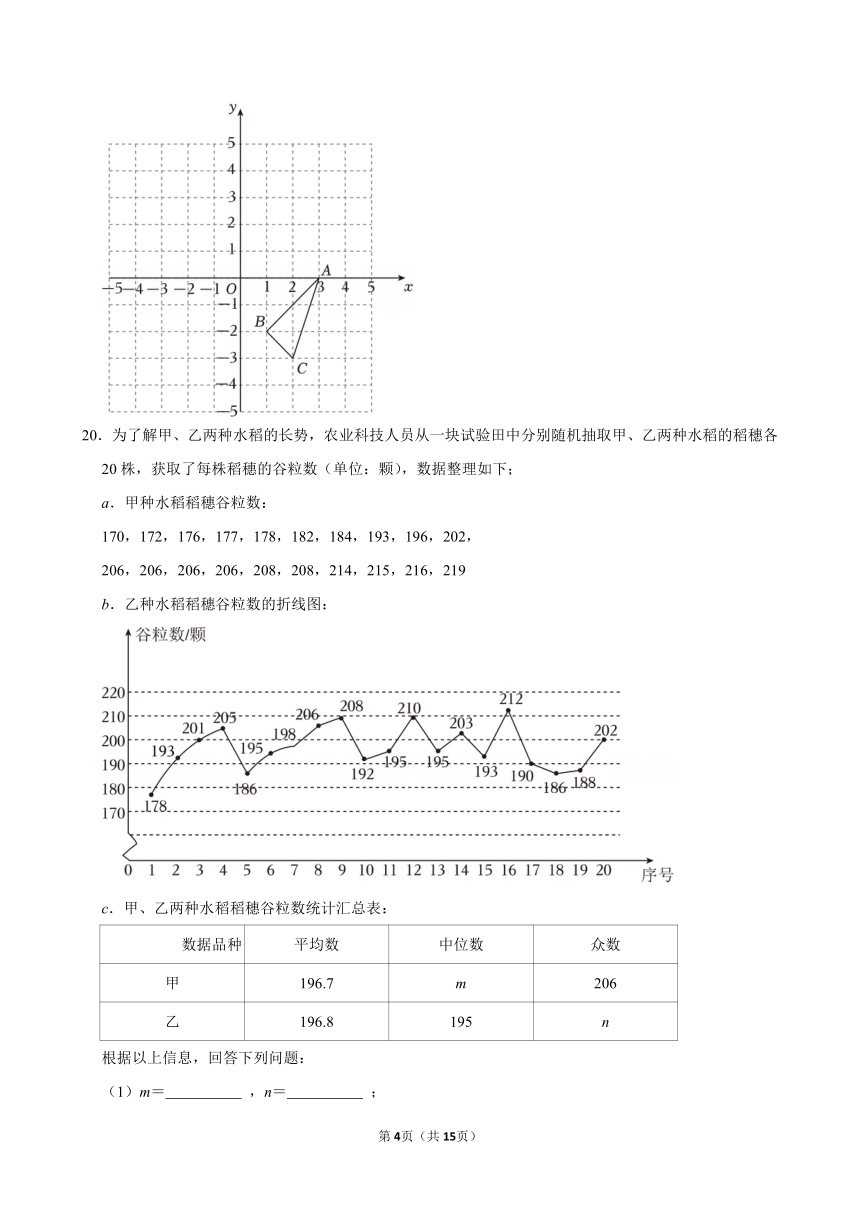
19.在平面直角坐标系xOy中,已知△ABC.
(1)画出与△ABC关于原点对称的△A1B1C1;
(2)以原点O为中心,把△ABC逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
20.为了解甲、乙两种水稻的长势,农业科技人员从一块试验田中分别随机抽取甲、乙两种水稻的稻穗各20株,获取了每株稻穗的谷粒数(单位:颗),数据整理如下;
a.甲种水稻稻穗谷粒数:
170,172,176,177,178,182,184,193,196,202,
206,206,206,206,208,208,214,215,216,219
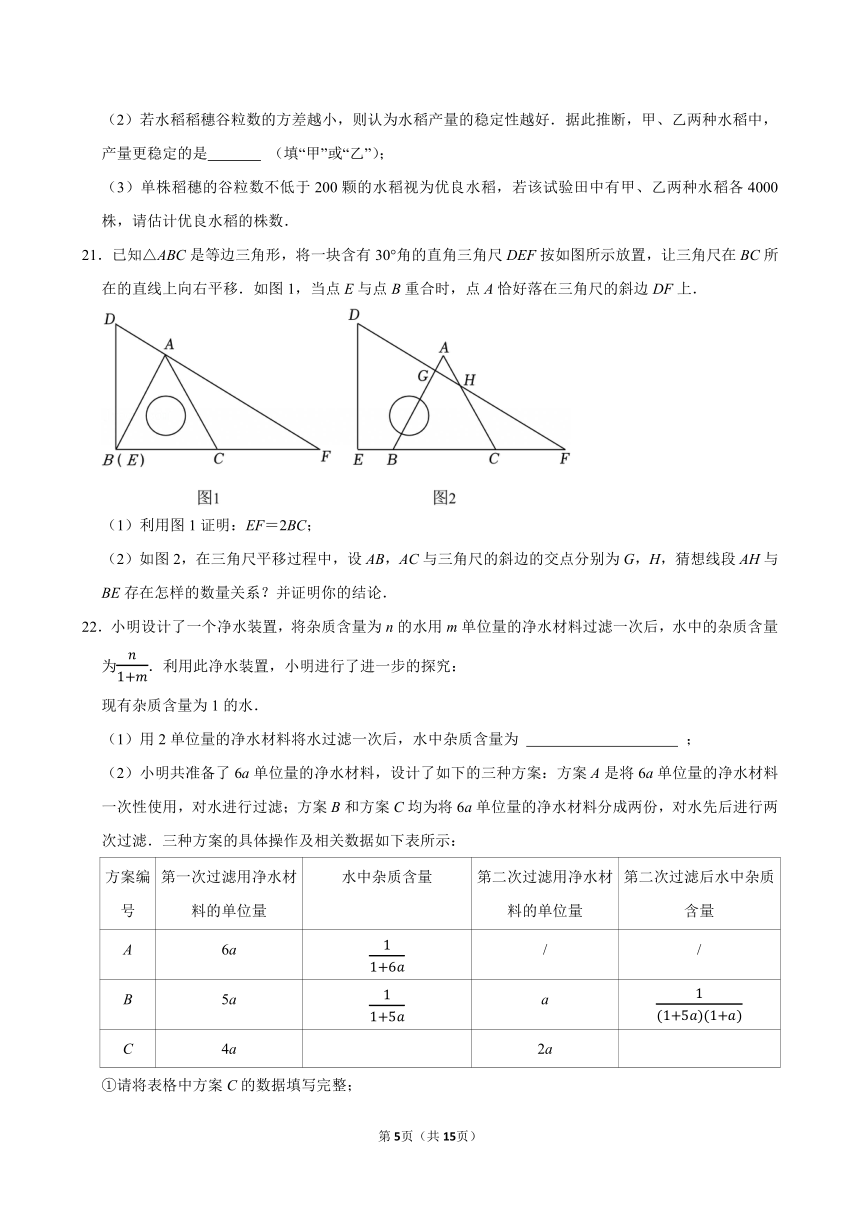
b.乙种水稻稻穗谷粒数的折线图:
c.甲、乙两种水稻稻穗谷粒数统计汇总表:
数据品种 平均数 中位数 众数
甲 196.7 m 206
乙 196.8 195 n
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)若水稻稻穗谷粒数的方差越小,则认为水稻产量的稳定性越好.据此推断,甲、乙两种水稻中,产量更稳定的是 (填“甲”或“乙”);
(3)单株稻穗的谷粒数不低于200颗的水稻视为优良水稻,若该试验田中有甲、乙两种水稻各4000株,请估计优良水稻的株数.
21.已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图1,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图1证明:EF=2BC;
(2)如图2,在三角尺平移过程中,设AB,AC与三角尺的斜边的交点分别为G,H,猜想线段AH与BE存在怎样的数量关系?并证明你的结论.
22.小明设计了一个净水装置,将杂质含量为n的水用m单位量的净水材料过滤一次后,水中的杂质含量为.利用此净水装置,小明进行了进一步的探究:
现有杂质含量为1的水.
(1)用2单位量的净水材料将水过滤一次后,水中杂质含量为 ;
(2)小明共准备了6a单位量的净水材料,设计了如下的三种方案:方案A是将6a单位量的净水材料一次性使用,对水进行过滤;方案B和方案C均为将6a单位量的净水材料分成两份,对水先后进行两次过滤.三种方案的具体操作及相关数据如下表所示:
方案编号 第一次过滤用净水材料的单位量 水中杂质含量 第二次过滤用净水材料的单位量 第二次过滤后水中杂质含量
A 6a / /
B 5a a
C 4a 2a
①请将表格中方案C的数据填写完整;
②通过计算回答:在这三种方案中,哪种方案的最终过滤效果最好?
(3)当净水材料总量为6a单位量不变时,为了使两次过滤后水中的杂质含量最少,小明应将第一次净水材料用量定为 (用含a的式子表示).
23.如图,点D为等腰直角三角形ABC斜边AC上一动点(点D不与线段AC两端点重合),将BD绕点B顺时针方向旋转90°到BE,连接AE、EC、ED.
(1)求证:AD=EC;
(2)若AD=1,CD=7,求BD的长;
(3)若AC2=40,请直接写出AE+BE的最小值.
2024-2025学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A D D A B B D D
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.解:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、是轴对称图形,是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:C.
2.解:由题意,得
x﹣2≠0,解得x≠2,
故选:C.
3.解:原式=(x﹣2)(x+8),
故选:A.
4.解:∵a+b=3,ab=1,
∴原式=a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2
=1×32
=9,
故选:D.
5.解:由“上加下减,左减右加”的平移规律可知,在平面直角坐标系中,将点P(4,3)向右平移2个单位长度,再向下平移2个单位长度所得到的点的坐标为(4+2,3﹣2),即(6,1),
故选:D.
6.解:把这些数从小到大排列,最中间两个数的平均数是(40+40)÷2=40,则中位数是40,故A选项正确;
40出现的次数最多,出现了4次,则众数是40,故B选项错误;
这组数据的平均数(25+30×2+40×4+50×2+60)÷10=40.5,故C选项错误;
这组数据的极差是:60﹣25=35,故D选项错误;
故选A.
7.解:去分母得:2=x﹣1﹣m,
解得:x=m+3,
由方程的解为正数,得到m+3>0,且m+3≠1,
则m的范围为m>﹣3且m≠﹣2.
故选:B.
8.解:设设原计划平均每天修x米,实际每天铺设管道(x﹣10)米,
方程5,则表示实际用的时间﹣原计划用的时间=5天,
那么就说明每天比原计划少铺设10米,结果延期5天才完成.
故选:B.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故A错误,C错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC,∠CBE,
∴∠A=∠EBC,故D正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故B错误
故选:D.
10.解:由题知,
BD由BP绕点B逆时针旋转60°得到,
∴BP=BD,∠PBD=60°.
又∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∴∠ABD+∠ABP=∠CBP+∠ABP,
∴∠ABD=∠CBP.
在△BDA和△BPC中,
,
∴△BDA≌△BPC(SAS).
故①正确.
∵BP=BD,
∴△BDP是等腰三角形,
又∵∠PBD=60°,
∴△BDP是等边三角形.
故②正确.
∵△BDP是等边三角形,
∴∠BDP=60°,PD=PB.
∵∠BPC=150°,
∴∠ADP=150°﹣60°=90°.
在Rt△ADP中,
PA2=PD2+AD2.
∵△BDA≌△BPC,
∴AD=PC,
∴PA2=PB2+PC2.
故③正确.
故选:D.
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.解:依题意,得
x﹣2=0,且x≠0,
解得,x=2.
故答案为:2.
12.解:点P(1,2)关于原点对称的点的坐标是(﹣1,﹣2),
故答案为:(﹣1,﹣2).
13.解:平均数为=(1+2+3+4+5)÷5=3,
S2[(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
故答案为:2.
14.解:∵将△OAB绕点O逆时针旋转70°到△OCD,
∴∠DOB=70°,
∵∠AOB=40°,
∴∠AOD=∠BOD﹣∠AOB=30°,
故答案为:30.
15.解:先分别表示出a2,a3,a4,a5,……,
∵a1=x+1,
∴;
;
;
;
……,
2025÷3=675,
∴.
故答案为:.
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共90分)
16.解:(1)原式=2(x2﹣4)
=2(x+2)(x﹣2);
(2)原式=x2+2x+4x+8+1
=x2+6x+9
=(x+3)2.
17.解:(1)原式
;
(2)原式
.
18.解:(1)去分母得:3(x﹣2)+(x+2)(x﹣2)=x(x+2),
去括号得:3x﹣6+x2﹣4=x2+2x,
移项得:3x+x2﹣x2﹣2x=4+6,
合并同类项得:x=10,
检验,当x=10时,(x+2)(x﹣2)≠0,
∴x=10是原方程的解;
(2)去分母得:2+x(x+1)=(x+1)(x﹣1),
去括号得:2+x2+x=x2﹣1,
移项得:x2+x﹣x2=﹣1﹣2,
合并同类项得:x=﹣3,
检验,当x=﹣3时,(x+1)(x﹣1)≠0,
∴x=﹣3是原方程的解.
19.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
20.解:(1)将甲的数据从小到大排列,可以发现一共20个数据,第10个数据为202,第11个数据为206,所以这组数据的中位数为,
∴m=204;
根据乙种水稻稻穗谷粒数的折线图可以发现,每柱稻穗的谷粒为195出现的次数最多,也就是说这组数据的众数为195,
∴n=195.
故答案为:204,195;
(2)根据整理出的数据可得,乙的平均数、中位数、众数都比较接近,故乙更稳定,
故答案为:乙;
(3)甲的水稻优良率为:,
乙的水稻优良率为:,
若该实验田中有甲、乙两种水稻各4000株,
则甲的优良水稻有4000×55%=2200(株),
乙的优良水稻有4000×40%=1600(株),
∴共有(株).
答:优良水稻株数为3800株.
21.(1)证明:由题意得,∠F=30°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠CAF=∠ACB﹣∠F=60°﹣30°=30°,
∴∠CAF=∠F=30°,
∴CA=CF,
∴BC=CF,
∴EF=2BC;
(2)解:AH=BE,证明如下:
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠CHF=∠ACB﹣∠F=60°﹣30°=30°,
∴∠CHF=∠F,
∴CF=CH,
∵EF=2BC,
∴BE+CF=BC,
又∵AC=AH+CH,AC=BC,
∴AH=BE.
22.解:(1)水中的杂质含量为,
∴现有杂质含量为1的水,用2单位量的净水材料将水过滤一次后,水中杂质含量为 ,
故答案为:.
(2)①方案C水中杂质含量:,第二次过滤后水中杂质含量:;
②,
∵a>0,
∴5a2>0,(1+6a)(1+5a)(1+a)>0
∴,
同理可得:,
∴,
∴方案C的最终过滤效果最好;
(3)将第一次净水材料用量定为3a时,第二次过滤后水中杂质含量为;
将第一次净水材料用量定为2a时,第二次过滤后水中杂质含量为,结果与将第一次净水材料用量定为4a时相同;
将第一次净水材料用量定为a时,第二次过滤后水中杂质含量为,结果与将第一次净水材料用量定为5a时相同;
∵在将第一次净水材料用量定为6a、5a、4a时,4a的最终过滤效果最好,
同理,可得0,
∴将第一次净水材料用量定为3a时,其最终过滤效果最好,
∴为了使两次过滤后水中的杂质含量最少,小明应将第一次净水材料用量定为3a.
故答案为:3a.
23.(1)证明:∵将BD绕点B顺时针方向旋转90°到BE,
∴BD=BE,∠DBE=90°,
∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABD=∠EBC,
∴△ABD≌△CBE(SAS),
∴AD=EC;
(2)解:∵△ABD≌△CBE,
∴∠BAD=∠BCE=45°,
∴∠DCE=∠DCB+BCE=90°,
在Rt△DCE中,由勾股定理得,DE2=72+12=50,
∵△BDE是等腰直角三角形,
∴DE2=2BD2=50
∴BD=5;
(3)解:由(2)知,∠BCE=45°,
则点E在直线CE上运动,
作点B关于CE的对称点B',连接AB',交GC于E,此时AE+BE最小,
∵AC2=40,
∴AB2=BG2=GB'2=20,
∴AG2=(2AB)2=80,
在Rt△AGB'中,由勾股定理得,AB'2=AG2+B'G2=80+20=100,
∴AB'=10,
∴AE+BE的最小值为10.
第1页(共1页)
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.(4分)下列图形既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(4分)分式有意义,则x的取值范围是( )
A.x>2 B.x=2 C.x≠2 D.x<2
3.(4分)将多项式x2+6x﹣16因式分解,正确的是( )
A.(x﹣2)(x+8) B.(x+2)(x﹣8)
C.(x+4)(x﹣4) D.(x﹣4)2
4.(4分)如果a+b=3,ab=1,那么a3b+2a2b2+ab3的值为( )
A.0 B.1 C.4 D.9
5.(4分)在平面直角坐标系中,将点P(4,3)向右平移2个单位长度,再向下平移2个单位长度所得到的点的坐标为( )
A.(2,1) B.(2,3) C.(6,5) D.(6,1)
6.(4分)为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表:
月用电量(度) 25 30 40 50 60
户数 1 2 4 2 1
关于这10户家庭的月用电量说法正确的是( )
A.中位数是40 B.众数是4
C.平均数是20.5 D.极差是3
7.(4分)分式方程1的解为正数,则m的取值范围( )
A.m>﹣3 B.m>﹣3且m≠﹣2
C.m<3 D.m<3且m≠﹣2
8.(4分)某市工程队要修路1000米,因天气原因,实施施工时“…”,设原计划平均每天修x米,则可得方程5,根据此情景,题中用“…”表示的缺失的条件应为( )
A.每天比原计划多铺设10米,结果延期5天才完成
B.每天比原计划少铺设10米,结果延期5天才完成
C.每天比原计划多铺设10米,结果提前5天完成了
D.每天比原计划少铺设10米,结果提前5天完成了
9.(4分)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC
10.(4分)如图,在等边三角形ABC中,有一点P,连接PA、PB、PC,将BP绕点B逆时针旋转60°得到BD,连接PD、AD,有如下结论:①△BPC≌△BDA;②△BDP是等边三角形;③如果∠BPC=150°,那么PA2=PB2+PC2.以上结论正确的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.(4分)如果分式的值为零,那么x的值为 .
12.(4分)在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是 .
13.(4分)已知一组数据为1,2,3,4,5,则这组数据的方差为 .
14.(4分)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD的大小为 度.
15.(4分)已知a1=x+1(x≠0且x≠﹣1),,,…,,则a2025的值为 .
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共90分)
16.分解因式:
(1)2x2﹣8
(2)(x+2)(x+4)+1
17.计算:
(1)
(2)
18.解方程:
(1)
(2)
19.在平面直角坐标系xOy中,已知△ABC.
(1)画出与△ABC关于原点对称的△A1B1C1;
(2)以原点O为中心,把△ABC逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
20.为了解甲、乙两种水稻的长势,农业科技人员从一块试验田中分别随机抽取甲、乙两种水稻的稻穗各20株,获取了每株稻穗的谷粒数(单位:颗),数据整理如下;
a.甲种水稻稻穗谷粒数:
170,172,176,177,178,182,184,193,196,202,
206,206,206,206,208,208,214,215,216,219
b.乙种水稻稻穗谷粒数的折线图:
c.甲、乙两种水稻稻穗谷粒数统计汇总表:
数据品种 平均数 中位数 众数
甲 196.7 m 206
乙 196.8 195 n
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)若水稻稻穗谷粒数的方差越小,则认为水稻产量的稳定性越好.据此推断,甲、乙两种水稻中,产量更稳定的是 (填“甲”或“乙”);
(3)单株稻穗的谷粒数不低于200颗的水稻视为优良水稻,若该试验田中有甲、乙两种水稻各4000株,请估计优良水稻的株数.
21.已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图1,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图1证明:EF=2BC;
(2)如图2,在三角尺平移过程中,设AB,AC与三角尺的斜边的交点分别为G,H,猜想线段AH与BE存在怎样的数量关系?并证明你的结论.
22.小明设计了一个净水装置,将杂质含量为n的水用m单位量的净水材料过滤一次后,水中的杂质含量为.利用此净水装置,小明进行了进一步的探究:
现有杂质含量为1的水.
(1)用2单位量的净水材料将水过滤一次后,水中杂质含量为 ;
(2)小明共准备了6a单位量的净水材料,设计了如下的三种方案:方案A是将6a单位量的净水材料一次性使用,对水进行过滤;方案B和方案C均为将6a单位量的净水材料分成两份,对水先后进行两次过滤.三种方案的具体操作及相关数据如下表所示:
方案编号 第一次过滤用净水材料的单位量 水中杂质含量 第二次过滤用净水材料的单位量 第二次过滤后水中杂质含量
A 6a / /
B 5a a
C 4a 2a
①请将表格中方案C的数据填写完整;
②通过计算回答:在这三种方案中,哪种方案的最终过滤效果最好?
(3)当净水材料总量为6a单位量不变时,为了使两次过滤后水中的杂质含量最少,小明应将第一次净水材料用量定为 (用含a的式子表示).
23.如图,点D为等腰直角三角形ABC斜边AC上一动点(点D不与线段AC两端点重合),将BD绕点B顺时针方向旋转90°到BE,连接AE、EC、ED.
(1)求证:AD=EC;
(2)若AD=1,CD=7,求BD的长;
(3)若AC2=40,请直接写出AE+BE的最小值.
2024-2025学年山东省淄博市周村区八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A D D A B B D D
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共40分)
1.解:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、是轴对称图形,是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:C.
2.解:由题意,得
x﹣2≠0,解得x≠2,
故选:C.
3.解:原式=(x﹣2)(x+8),
故选:A.
4.解:∵a+b=3,ab=1,
∴原式=a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2
=1×32
=9,
故选:D.
5.解:由“上加下减,左减右加”的平移规律可知,在平面直角坐标系中,将点P(4,3)向右平移2个单位长度,再向下平移2个单位长度所得到的点的坐标为(4+2,3﹣2),即(6,1),
故选:D.
6.解:把这些数从小到大排列,最中间两个数的平均数是(40+40)÷2=40,则中位数是40,故A选项正确;
40出现的次数最多,出现了4次,则众数是40,故B选项错误;
这组数据的平均数(25+30×2+40×4+50×2+60)÷10=40.5,故C选项错误;
这组数据的极差是:60﹣25=35,故D选项错误;
故选A.
7.解:去分母得:2=x﹣1﹣m,
解得:x=m+3,
由方程的解为正数,得到m+3>0,且m+3≠1,
则m的范围为m>﹣3且m≠﹣2.
故选:B.
8.解:设设原计划平均每天修x米,实际每天铺设管道(x﹣10)米,
方程5,则表示实际用的时间﹣原计划用的时间=5天,
那么就说明每天比原计划少铺设10米,结果延期5天才完成.
故选:B.
9.解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故A错误,C错误;
∴∠ACD=∠BCE,
∴∠A=∠ADC,∠CBE,
∴∠A=∠EBC,故D正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故B错误
故选:D.
10.解:由题知,
BD由BP绕点B逆时针旋转60°得到,
∴BP=BD,∠PBD=60°.
又∵△ABC是等边三角形,
∴∠ABC=60°,AB=BC,
∴∠ABD+∠ABP=∠CBP+∠ABP,
∴∠ABD=∠CBP.
在△BDA和△BPC中,
,
∴△BDA≌△BPC(SAS).
故①正确.
∵BP=BD,
∴△BDP是等腰三角形,
又∵∠PBD=60°,
∴△BDP是等边三角形.
故②正确.
∵△BDP是等边三角形,
∴∠BDP=60°,PD=PB.
∵∠BPC=150°,
∴∠ADP=150°﹣60°=90°.
在Rt△ADP中,
PA2=PD2+AD2.
∵△BDA≌△BPC,
∴AD=PC,
∴PA2=PB2+PC2.
故③正确.
故选:D.
二、填空题:请将最终结果填入题中的横线上(每小题4分,共20分)
11.解:依题意,得
x﹣2=0,且x≠0,
解得,x=2.
故答案为:2.
12.解:点P(1,2)关于原点对称的点的坐标是(﹣1,﹣2),
故答案为:(﹣1,﹣2).
13.解:平均数为=(1+2+3+4+5)÷5=3,
S2[(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
故答案为:2.
14.解:∵将△OAB绕点O逆时针旋转70°到△OCD,
∴∠DOB=70°,
∵∠AOB=40°,
∴∠AOD=∠BOD﹣∠AOB=30°,
故答案为:30.
15.解:先分别表示出a2,a3,a4,a5,……,
∵a1=x+1,
∴;
;
;
;
……,
2025÷3=675,
∴.
故答案为:.
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共90分)
16.解:(1)原式=2(x2﹣4)
=2(x+2)(x﹣2);
(2)原式=x2+2x+4x+8+1
=x2+6x+9
=(x+3)2.
17.解:(1)原式
;
(2)原式
.
18.解:(1)去分母得:3(x﹣2)+(x+2)(x﹣2)=x(x+2),
去括号得:3x﹣6+x2﹣4=x2+2x,
移项得:3x+x2﹣x2﹣2x=4+6,
合并同类项得:x=10,
检验,当x=10时,(x+2)(x﹣2)≠0,
∴x=10是原方程的解;
(2)去分母得:2+x(x+1)=(x+1)(x﹣1),
去括号得:2+x2+x=x2﹣1,
移项得:x2+x﹣x2=﹣1﹣2,
合并同类项得:x=﹣3,
检验,当x=﹣3时,(x+1)(x﹣1)≠0,
∴x=﹣3是原方程的解.
19.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
20.解:(1)将甲的数据从小到大排列,可以发现一共20个数据,第10个数据为202,第11个数据为206,所以这组数据的中位数为,
∴m=204;
根据乙种水稻稻穗谷粒数的折线图可以发现,每柱稻穗的谷粒为195出现的次数最多,也就是说这组数据的众数为195,
∴n=195.
故答案为:204,195;
(2)根据整理出的数据可得,乙的平均数、中位数、众数都比较接近,故乙更稳定,
故答案为:乙;
(3)甲的水稻优良率为:,
乙的水稻优良率为:,
若该实验田中有甲、乙两种水稻各4000株,
则甲的优良水稻有4000×55%=2200(株),
乙的优良水稻有4000×40%=1600(株),
∴共有(株).
答:优良水稻株数为3800株.
21.(1)证明:由题意得,∠F=30°,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠CAF=∠ACB﹣∠F=60°﹣30°=30°,
∴∠CAF=∠F=30°,
∴CA=CF,
∴BC=CF,
∴EF=2BC;
(2)解:AH=BE,证明如下:
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠CHF=∠ACB﹣∠F=60°﹣30°=30°,
∴∠CHF=∠F,
∴CF=CH,
∵EF=2BC,
∴BE+CF=BC,
又∵AC=AH+CH,AC=BC,
∴AH=BE.
22.解:(1)水中的杂质含量为,
∴现有杂质含量为1的水,用2单位量的净水材料将水过滤一次后,水中杂质含量为 ,
故答案为:.
(2)①方案C水中杂质含量:,第二次过滤后水中杂质含量:;
②,
∵a>0,
∴5a2>0,(1+6a)(1+5a)(1+a)>0
∴,
同理可得:,
∴,
∴方案C的最终过滤效果最好;
(3)将第一次净水材料用量定为3a时,第二次过滤后水中杂质含量为;
将第一次净水材料用量定为2a时,第二次过滤后水中杂质含量为,结果与将第一次净水材料用量定为4a时相同;
将第一次净水材料用量定为a时,第二次过滤后水中杂质含量为,结果与将第一次净水材料用量定为5a时相同;
∵在将第一次净水材料用量定为6a、5a、4a时,4a的最终过滤效果最好,
同理,可得0,
∴将第一次净水材料用量定为3a时,其最终过滤效果最好,
∴为了使两次过滤后水中的杂质含量最少,小明应将第一次净水材料用量定为3a.
故答案为:3a.
23.(1)证明:∵将BD绕点B顺时针方向旋转90°到BE,
∴BD=BE,∠DBE=90°,
∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABD=∠EBC,
∴△ABD≌△CBE(SAS),
∴AD=EC;
(2)解:∵△ABD≌△CBE,
∴∠BAD=∠BCE=45°,
∴∠DCE=∠DCB+BCE=90°,
在Rt△DCE中,由勾股定理得,DE2=72+12=50,
∵△BDE是等腰直角三角形,
∴DE2=2BD2=50
∴BD=5;
(3)解:由(2)知,∠BCE=45°,
则点E在直线CE上运动,
作点B关于CE的对称点B',连接AB',交GC于E,此时AE+BE最小,
∵AC2=40,
∴AB2=BG2=GB'2=20,
∴AG2=(2AB)2=80,
在Rt△AGB'中,由勾股定理得,AB'2=AG2+B'G2=80+20=100,
∴AB'=10,
∴AE+BE的最小值为10.
第1页(共1页)
同课章节目录
