2025年云南省昆明实验中学中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年云南省昆明实验中学中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 221.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 08:59:00 | ||
图片预览




文档简介
2025年云南省昆明实验中学中考数学模拟试卷
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我国古代数学名著《九章算术》在“方程”章中首次出现了负数,如“卖所得的钱为正,买所付的钱为负,余钱为正,不足钱为负”.如果收入300元记作+300元,那么-90元表示( )
A. 支出210元 B. 收入210元 C. 支出90元 D. 收入90元
2.中国文字博大精深,而且有许多是轴对称图形,在这四个美术字中,是轴对称图形的是( )
A. 盛 B. 世 C. 中 D. 国
3.中国空间站(又称天宫空间站)是中华人民共和国建成的国家级太空实验室,其轨道高度设定在约425000米,设定寿命为10年,可以长期驻留3人,最大可扩展为180吨级六舱组合体,以进行较大规模的空间应用.将数据425000用科学记数法表示为( )
A. 42.5×104 B. 0.425×106 C. 4.25×105 D. 4.25×106
4.下列运算正确的是( )
A. a2+a2=a4 B. 2a3b÷ab=2a2b C. a2 a4=a6 D. (a-1)2=a2-1
5.如图是某几何体的主视图、左视图、俯视图,该几何体是( )
A. 长方体
B. 球
C. 三棱柱
D. 圆柱
6.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A. 70°
B. 65°
C. 50°
D. 40°
7.关于x的方程kx2+2x-1=0有实数根,则k的取值范围是( )
A. k≥-1 B. k≥-1且k≠0 C. k≤-1 D. k≤1且k≠0
8.一个八边形的内角和等于( )
A. 800° B. 1080° C. 1260° D. 1440°
9.如图,在△ABC中,∠ABC=90°,若AC=5,BC=4,则tanA的值为( )
A.
B.
C.
D.
10.学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校八年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:
课外书数量(本) 6 7 9 12
人数 6 7 10 7
则阅读课外书数量的中位数和众数分别是( )
A. 8,9 B. 10,9 C. 7,12 D. 9,9
11.反比例函数y=的图象一定经过的点是( )
A. (-3,2) B. (2,-3) C. (-2,-4) D. (2,3)
12.以下是一组按一定规律排列的多项式:a+b,a2+2b,a3+3b,a4+4b,a5+5b,…,则第n个多项式是( )
A. an+(n-1)b B. an+nb C. an+(n+1)b D. an+1+nb
13.如图,在新能源汽车的动力传输系统模拟图中,四边形ABCD形似一个关键的传动装置连接结构,该四边形内接于⊙O,AC为对角线且恰好经过圆心O.已知在某一时刻,∠ACD=30°,则∠DBC的度数为( )
A. 30° B. 45° C. 60° D. 75°
14.小米给过生日的弟弟做了一顶圆锥形的生日帽,经过测量这顶圆锥形帽的母线长度为30厘米,底面圆的半径为15厘米,则该圆锥帽的侧面积为( )
A. 225平方厘米 B. 900π平方厘米 C. 1200π平方厘米 D. 450π平方厘米
15.“指尖上的非遗一一麻柳刺绣”,针线勾勒之间,绣出世间百态.在一幅长80cm,宽50cm的刺绣风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为( )
A. (50+x)(80+x)=5400 B. (50-x)(80-x)=5400
C. (50+2x)(80+2x)=5400 D. (50-2x)(80-2x)=5400
二、填空题:本题共4小题,每小题2分,共8分。
16.若二次根式有意义,则x的取值范围是______.
17.分解因式:x3-25x= ______.
18.如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1:4,若AB=6,则CD的长为______.
19.为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计.图(1)与图(2)是整理数据后绘制的两幅不完整的统计图.以下结论正确的是______.
①由这两个统计图可知喜好“科普常识”的学生有90人;
②若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360人
③在扇形统计图中,“漫画”所在扇形的圆心角为72°
④这两个统计图不能确定喜好“小说”的人数.
三、解答题:本题共8小题,共62分。解答应写出文字说明,证明过程或演算步骤。
20.(本小题6分)
计算:.
21.(本小题8分)
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠B=∠E=90°,AB=DE,AF=CD.求证:△ABC≌△DEF.
22.(本小题8分)
云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
23.(本小题8分)
人工智能是数字经济高质量发展的引擎,也是新一轮科技革命和产业变革的重要驱动力.为进一步了解学习,小明打算先从比较热门的人工智能软件随机选择,现有如下四种AI软件,他将四种图标依次制成A,B,C,D四张卡片(卡片的形状、大小、质地都相同),将四张卡片背面朝上洗匀放置在桌面上.
A.豆包B.Deepseek C.Kimi D.文心一言
(1)从中随机抽取一张,抽到Deepseek卡片的概率为______;
(2)从中随机抽取一张不放回,洗匀后再随机抽取一张,请用列表或画树状图的方法求两次抽取到的卡片中,含有Deepseek卡片的概率.
24.(本小题8分)
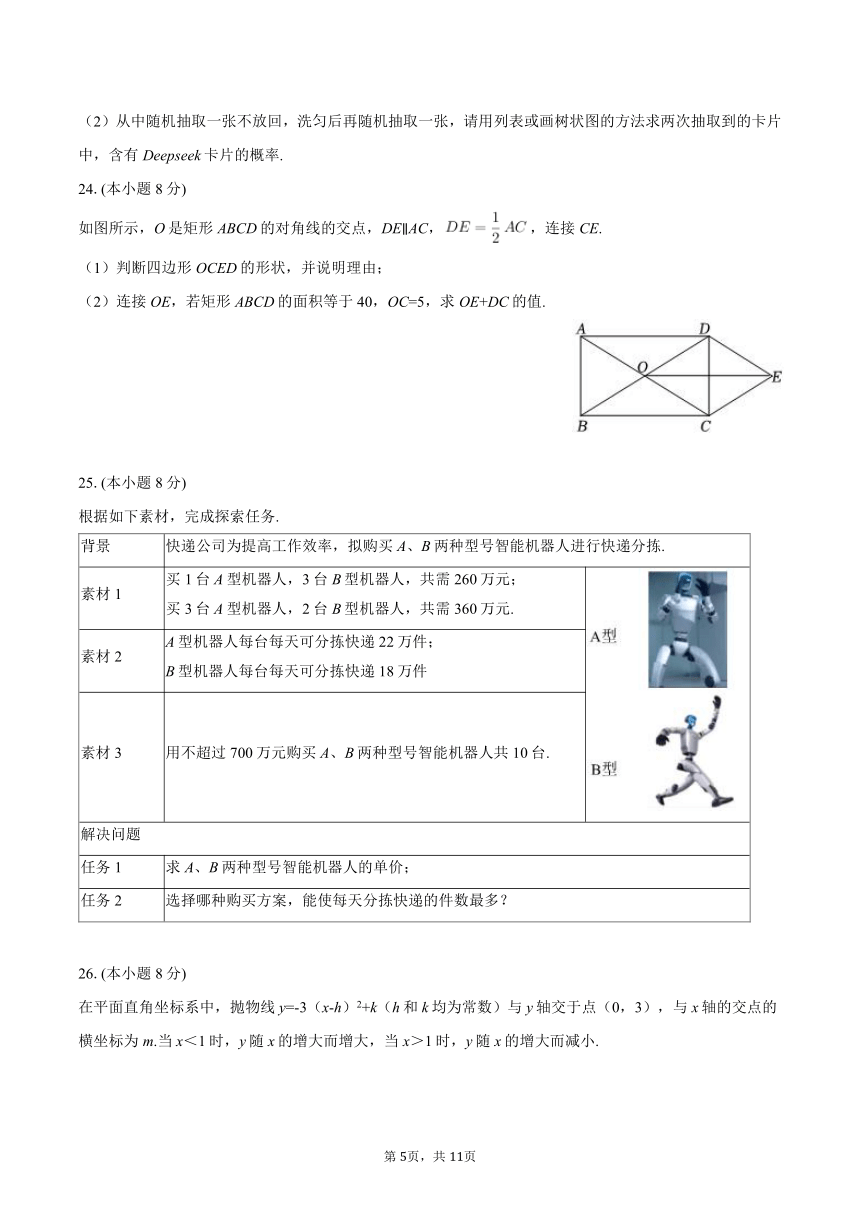
如图所示,O是矩形ABCD的对角线的交点,DE∥AC,,连接CE.
(1)判断四边形OCED的形状,并说明理由;
(2)连接OE,若矩形ABCD的面积等于40,OC=5,求OE+DC的值.
25.(本小题8分)
根据如下素材,完成探索任务.
背景 快递公司为提高工作效率,拟购买A、B两种型号智能机器人进行快递分拣.
素材1 买1台A型机器人,3台B型机器人,共需260万元;
买3台A型机器人,2台B型机器人,共需360万元.
素材2 A型机器人每台每天可分拣快递22万件;
B型机器人每台每天可分拣快递18万件
素材3 用不超过700万元购买A、B两种型号智能机器人共10台.
解决问题
任务1 求A、B两种型号智能机器人的单价;
任务2 选择哪种购买方案,能使每天分拣快递的件数最多?
26.(本小题8分)
在平面直角坐标系中,抛物线y=-3(x-h)2+k(h和k均为常数)与y轴交于点(0,3),与x轴的交点的横坐标为m.当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)若m>1,求证:.
27.(本小题8分)
如图,四边形ABCD是⊙O的内接四边形,AB=AD=6,∠BAD=90°,点E在弦AD上(不与端点重合),∠CBE=45°,过点C作CF⊥AD,垂足F在AD延长线上,连接CE.
(1)求⊙O的半径长;
(2)若∠DCF=∠ABE,求证:直线CF是QO的切线;
(3)过点D作DG⊥AD交⊙O于点G,交BC于连接EH,猜想∠AEH和∠AEB有怎样的数量关系,请证明你的结论.
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】B
13.【答案】C
14.【答案】D
15.【答案】C
16.【答案】x≤2
17.【答案】x(x+5)(x-5)
18.【答案】12
19.【答案】①②③
20.【答案】.
21.【答案】∵AF=CD,
∴AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴△ABC≌△DEF(HL).
22.【答案】实际每天采摘鲜叶550kg.
23.【答案】;
.
24.【答案】四边形OCED是菱形,∵四边形ABCD是矩形,
∴,
∴,
∵,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形,
∵OC=OD,
∴平行四边形OCED是菱形.;
6.
25.【答案】任务1:A型80万元,B型60万元;任务2:买5台A型,5台B型.
26.【答案】y=-3(x-1)2+6;
见解析.
27.【答案】(1)解:如图,连接BD,
∵∠BAD=90°,
∴BD是⊙O的直径,
在Rt△ABD 中,AB=AC=6,
由勾股定理得,
∴⊙O的半径.
(2)证明:如图,连接OC,
∵AB=AD,∠BAD=90°,
∴∠ABD=∠ADB=45°,
∵∠CBE=45°,
∴∠CBE-∠EBD=∠ABD-∠EBD,
即∠CBD=∠ABE,
∵∠DCF=∠ABE,
∴∠CBD=∠DCF,
又∵OB=OC,
∴∠CBD=∠OCB,
∴∠OCB=∠DCF,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠OCB+∠OCD=90°,
∴∠DCF+∠OCD=90°,
即∠OCF=90°,
∴OC⊥CF,
∵OC是⊙O 的半径,且OC⊥CF,
∴直线CF是⊙O的切线.
(3)解:∠AEH=2∠AEB,理由如下:
如图,连接BG,延长DA至点M,使得AM=GH,连接BM,
则∠BAM=180°-∠BAD=90°,
∵DG⊥AD,
∴∠ADG=90°,
∵四边形ABGD是CO的内接四边形,
∴∠ABG=180°-∠ADG=90°,
∠BGD=180°-∠BAD=90°,
∴∠BAM=∠BGH=90°,
∵∠BAD=∠ABG=∠ADG=90°,
∴四边形ABGD 是矩形,
又∵AB=AD,
∴四边形ABGD是正方形,
∴AB=BG,
在△BAM和△BGH中,
,
∴△BAM≌△BGH(SAS),
∴∠ABM=∠GBH,BM=BH,
∵∠ABG=90°,∠CBE=45°,
∴∠ABE+∠GBH=∠ABG-∠CBE=45°,
∴∠ABE+∠ABM=45°,
即∠MBE=45°,
∴∠EBM=∠EBH,
在△EBM和△EBH中,
,
∴△EBM≌△EBH(SAS),
∴∠BEM=∠BEH,
∴∠AEH=∠BEM+∠BEH=2∠BEM,
即∠AEH=2∠AEB.
第1页,共1页
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我国古代数学名著《九章算术》在“方程”章中首次出现了负数,如“卖所得的钱为正,买所付的钱为负,余钱为正,不足钱为负”.如果收入300元记作+300元,那么-90元表示( )
A. 支出210元 B. 收入210元 C. 支出90元 D. 收入90元
2.中国文字博大精深,而且有许多是轴对称图形,在这四个美术字中,是轴对称图形的是( )
A. 盛 B. 世 C. 中 D. 国
3.中国空间站(又称天宫空间站)是中华人民共和国建成的国家级太空实验室,其轨道高度设定在约425000米,设定寿命为10年,可以长期驻留3人,最大可扩展为180吨级六舱组合体,以进行较大规模的空间应用.将数据425000用科学记数法表示为( )
A. 42.5×104 B. 0.425×106 C. 4.25×105 D. 4.25×106
4.下列运算正确的是( )
A. a2+a2=a4 B. 2a3b÷ab=2a2b C. a2 a4=a6 D. (a-1)2=a2-1
5.如图是某几何体的主视图、左视图、俯视图,该几何体是( )
A. 长方体
B. 球
C. 三棱柱
D. 圆柱
6.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A. 70°
B. 65°
C. 50°
D. 40°
7.关于x的方程kx2+2x-1=0有实数根,则k的取值范围是( )
A. k≥-1 B. k≥-1且k≠0 C. k≤-1 D. k≤1且k≠0
8.一个八边形的内角和等于( )
A. 800° B. 1080° C. 1260° D. 1440°
9.如图,在△ABC中,∠ABC=90°,若AC=5,BC=4,则tanA的值为( )
A.
B.
C.
D.
10.学校举行“快乐阅读,健康成长”读书活动.小明随机调查了本校八年级30名同学近4个月内每人阅读课外书的数量,数据如下表所示:
课外书数量(本) 6 7 9 12
人数 6 7 10 7
则阅读课外书数量的中位数和众数分别是( )
A. 8,9 B. 10,9 C. 7,12 D. 9,9
11.反比例函数y=的图象一定经过的点是( )
A. (-3,2) B. (2,-3) C. (-2,-4) D. (2,3)
12.以下是一组按一定规律排列的多项式:a+b,a2+2b,a3+3b,a4+4b,a5+5b,…,则第n个多项式是( )
A. an+(n-1)b B. an+nb C. an+(n+1)b D. an+1+nb
13.如图,在新能源汽车的动力传输系统模拟图中,四边形ABCD形似一个关键的传动装置连接结构,该四边形内接于⊙O,AC为对角线且恰好经过圆心O.已知在某一时刻,∠ACD=30°,则∠DBC的度数为( )
A. 30° B. 45° C. 60° D. 75°
14.小米给过生日的弟弟做了一顶圆锥形的生日帽,经过测量这顶圆锥形帽的母线长度为30厘米,底面圆的半径为15厘米,则该圆锥帽的侧面积为( )
A. 225平方厘米 B. 900π平方厘米 C. 1200π平方厘米 D. 450π平方厘米
15.“指尖上的非遗一一麻柳刺绣”,针线勾勒之间,绣出世间百态.在一幅长80cm,宽50cm的刺绣风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为( )
A. (50+x)(80+x)=5400 B. (50-x)(80-x)=5400
C. (50+2x)(80+2x)=5400 D. (50-2x)(80-2x)=5400
二、填空题:本题共4小题,每小题2分,共8分。
16.若二次根式有意义,则x的取值范围是______.
17.分解因式:x3-25x= ______.
18.如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1:4,若AB=6,则CD的长为______.
19.为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计.图(1)与图(2)是整理数据后绘制的两幅不完整的统计图.以下结论正确的是______.
①由这两个统计图可知喜好“科普常识”的学生有90人;
②若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360人
③在扇形统计图中,“漫画”所在扇形的圆心角为72°
④这两个统计图不能确定喜好“小说”的人数.
三、解答题:本题共8小题,共62分。解答应写出文字说明,证明过程或演算步骤。
20.(本小题6分)
计算:.
21.(本小题8分)
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠B=∠E=90°,AB=DE,AF=CD.求证:△ABC≌△DEF.
22.(本小题8分)
云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
23.(本小题8分)
人工智能是数字经济高质量发展的引擎,也是新一轮科技革命和产业变革的重要驱动力.为进一步了解学习,小明打算先从比较热门的人工智能软件随机选择,现有如下四种AI软件,他将四种图标依次制成A,B,C,D四张卡片(卡片的形状、大小、质地都相同),将四张卡片背面朝上洗匀放置在桌面上.
A.豆包B.Deepseek C.Kimi D.文心一言
(1)从中随机抽取一张,抽到Deepseek卡片的概率为______;
(2)从中随机抽取一张不放回,洗匀后再随机抽取一张,请用列表或画树状图的方法求两次抽取到的卡片中,含有Deepseek卡片的概率.
24.(本小题8分)
如图所示,O是矩形ABCD的对角线的交点,DE∥AC,,连接CE.
(1)判断四边形OCED的形状,并说明理由;
(2)连接OE,若矩形ABCD的面积等于40,OC=5,求OE+DC的值.
25.(本小题8分)
根据如下素材,完成探索任务.
背景 快递公司为提高工作效率,拟购买A、B两种型号智能机器人进行快递分拣.
素材1 买1台A型机器人,3台B型机器人,共需260万元;
买3台A型机器人,2台B型机器人,共需360万元.
素材2 A型机器人每台每天可分拣快递22万件;
B型机器人每台每天可分拣快递18万件
素材3 用不超过700万元购买A、B两种型号智能机器人共10台.
解决问题
任务1 求A、B两种型号智能机器人的单价;
任务2 选择哪种购买方案,能使每天分拣快递的件数最多?
26.(本小题8分)
在平面直角坐标系中,抛物线y=-3(x-h)2+k(h和k均为常数)与y轴交于点(0,3),与x轴的交点的横坐标为m.当x<1时,y随x的增大而增大,当x>1时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)若m>1,求证:.
27.(本小题8分)
如图,四边形ABCD是⊙O的内接四边形,AB=AD=6,∠BAD=90°,点E在弦AD上(不与端点重合),∠CBE=45°,过点C作CF⊥AD,垂足F在AD延长线上,连接CE.
(1)求⊙O的半径长;
(2)若∠DCF=∠ABE,求证:直线CF是QO的切线;
(3)过点D作DG⊥AD交⊙O于点G,交BC于连接EH,猜想∠AEH和∠AEB有怎样的数量关系,请证明你的结论.
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】B
13.【答案】C
14.【答案】D
15.【答案】C
16.【答案】x≤2
17.【答案】x(x+5)(x-5)
18.【答案】12
19.【答案】①②③
20.【答案】.
21.【答案】∵AF=CD,
∴AC=DF.
在Rt△ABC和Rt△DEF中,
,
∴△ABC≌△DEF(HL).
22.【答案】实际每天采摘鲜叶550kg.
23.【答案】;
.
24.【答案】四边形OCED是菱形,∵四边形ABCD是矩形,
∴,
∴,
∵,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形,
∵OC=OD,
∴平行四边形OCED是菱形.;
6.
25.【答案】任务1:A型80万元,B型60万元;任务2:买5台A型,5台B型.
26.【答案】y=-3(x-1)2+6;
见解析.
27.【答案】(1)解:如图,连接BD,
∵∠BAD=90°,
∴BD是⊙O的直径,
在Rt△ABD 中,AB=AC=6,
由勾股定理得,
∴⊙O的半径.
(2)证明:如图,连接OC,
∵AB=AD,∠BAD=90°,
∴∠ABD=∠ADB=45°,
∵∠CBE=45°,
∴∠CBE-∠EBD=∠ABD-∠EBD,
即∠CBD=∠ABE,
∵∠DCF=∠ABE,
∴∠CBD=∠DCF,
又∵OB=OC,
∴∠CBD=∠OCB,
∴∠OCB=∠DCF,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠OCB+∠OCD=90°,
∴∠DCF+∠OCD=90°,
即∠OCF=90°,
∴OC⊥CF,
∵OC是⊙O 的半径,且OC⊥CF,
∴直线CF是⊙O的切线.
(3)解:∠AEH=2∠AEB,理由如下:
如图,连接BG,延长DA至点M,使得AM=GH,连接BM,
则∠BAM=180°-∠BAD=90°,
∵DG⊥AD,
∴∠ADG=90°,
∵四边形ABGD是CO的内接四边形,
∴∠ABG=180°-∠ADG=90°,
∠BGD=180°-∠BAD=90°,
∴∠BAM=∠BGH=90°,
∵∠BAD=∠ABG=∠ADG=90°,
∴四边形ABGD 是矩形,
又∵AB=AD,
∴四边形ABGD是正方形,
∴AB=BG,
在△BAM和△BGH中,
,
∴△BAM≌△BGH(SAS),
∴∠ABM=∠GBH,BM=BH,
∵∠ABG=90°,∠CBE=45°,
∴∠ABE+∠GBH=∠ABG-∠CBE=45°,
∴∠ABE+∠ABM=45°,
即∠MBE=45°,
∴∠EBM=∠EBH,
在△EBM和△EBH中,
,
∴△EBM≌△EBH(SAS),
∴∠BEM=∠BEH,
∴∠AEH=∠BEM+∠BEH=2∠BEM,
即∠AEH=2∠AEB.
第1页,共1页
同课章节目录
