2025年浙江省中考数学模拟试卷(四)(含部分答案)
文档属性
| 名称 | 2025年浙江省中考数学模拟试卷(四)(含部分答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 00:00:00 | ||
图片预览


文档简介
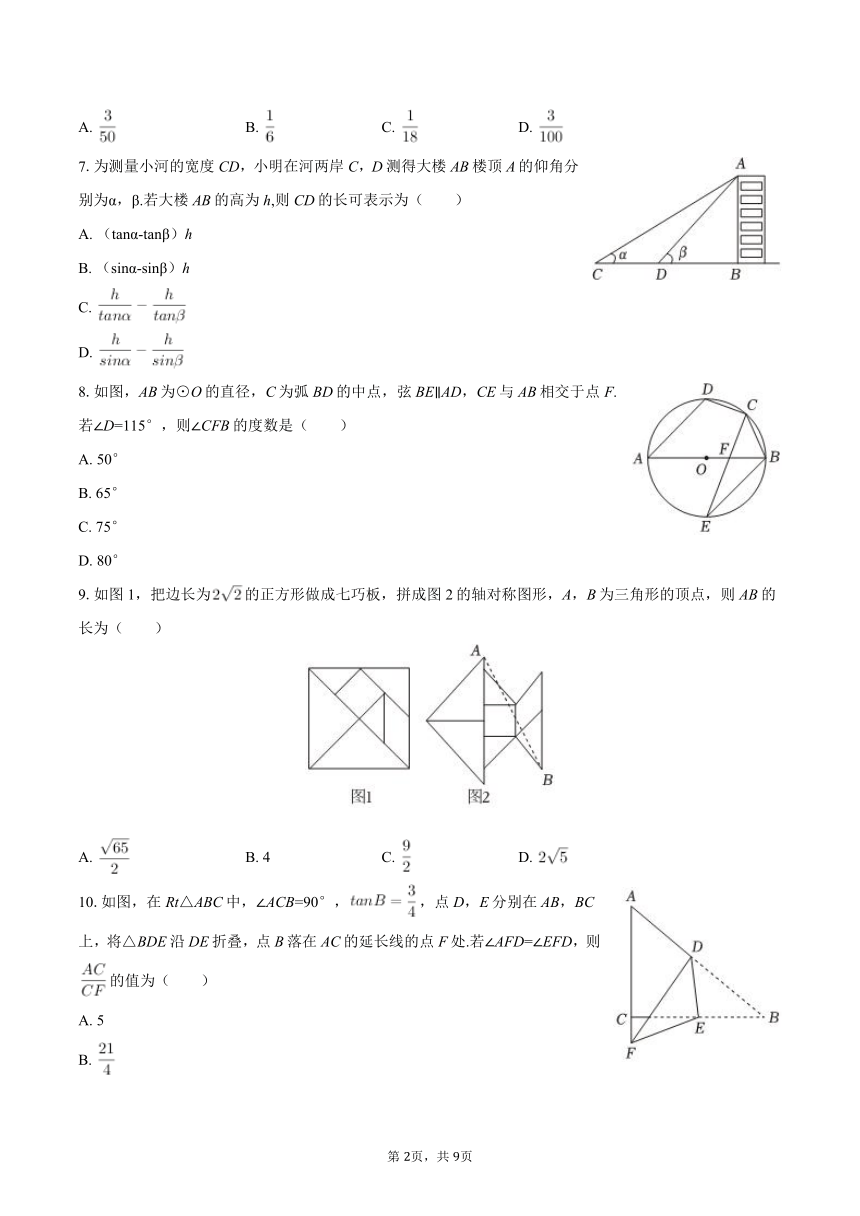
2025年浙江省中考数学模拟试卷(四)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.-5的相反数是( )
A. -5 B. 5 C. D. -
2.下列四个标志中,是轴对称图形的是( )
A. B. C. D.
3.2025年春节假期8天,全国国内出游501000000人次,数“501000000”用科学记数法可表示为( )
A. 0.501×108 B. 0.501×109 C. 5.01×108 D. 5.01×109
4.已知实数a,b满足a+b<0,若数a在数轴上对应点的位置如图所示,则数b所对应的点可以在( )
A. 线段BC上 B. 线段AB上 C. 线段CD上 D. 线段DE上
5.如图,根据尺规作图的痕迹,下列判断错误的是( )
A. 点O为AB,AC两条中垂线的交点
B. 点O到△ABC三个顶点的距离相等
C. 点O为△ABC的外接圆的圆心
D. 点O到△ABC三边的距离都相等
6.学校组织人工智能竞赛,成绩划分为A,B,C,D,E,F六个档次,小明随机抽取36名学生的竞赛成绩,并画出如图所示的统计图,若A,B为优秀,估计这次竞赛成绩的优秀率是( )
A. B. C. D.
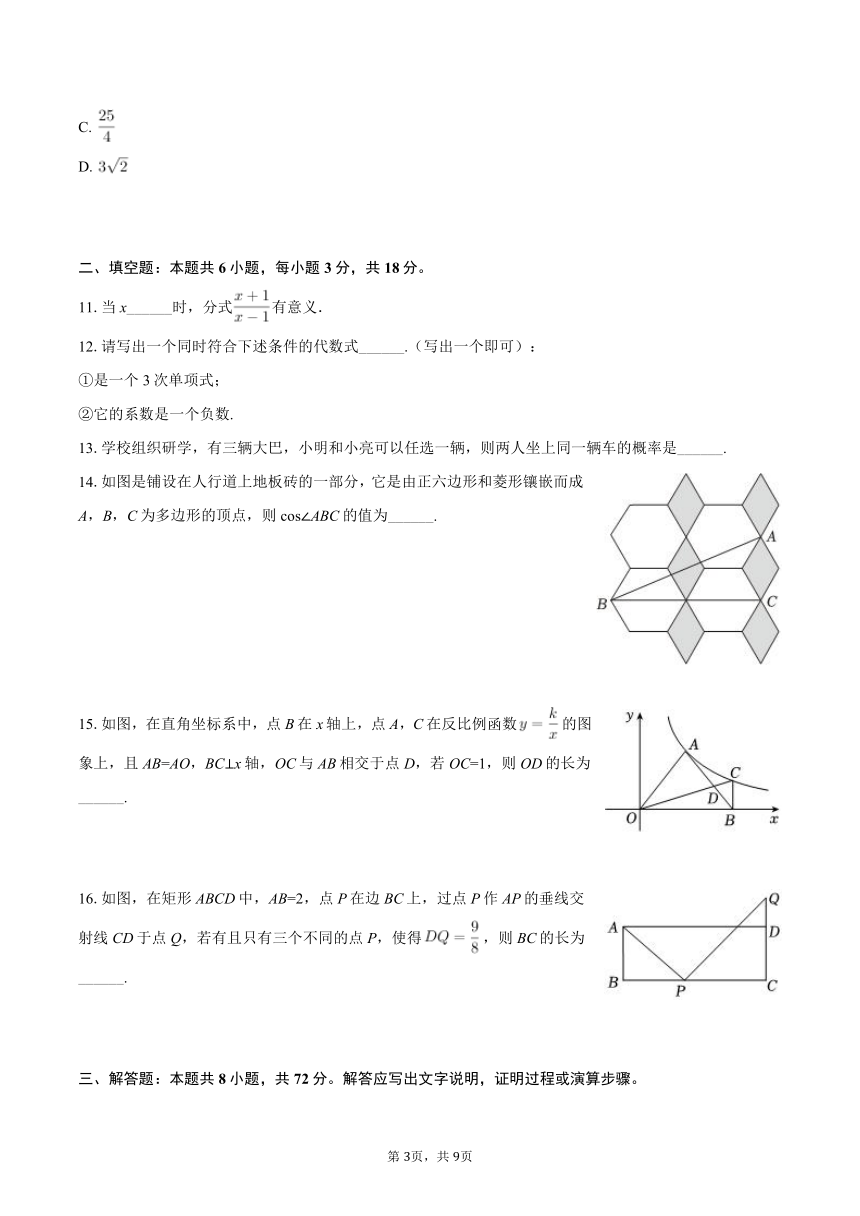
7.为测量小河的宽度CD,小明在河两岸C,D测得大楼AB楼顶A的仰角分别为α,β.若大楼AB的高为h,则CD的长可表示为( )
A. (tanα-tanβ)h
B. (sinα-sinβ)h
C.
D.
8.如图,AB为⊙O的直径,C为弧BD的中点,弦BE∥AD,CE与AB相交于点F.若∠D=115°,则∠CFB的度数是( )
A. 50°
B. 65°
C. 75°
D. 80°
9.如图1,把边长为的正方形做成七巧板,拼成图2的轴对称图形,A,B为三角形的顶点,则AB的长为( )
A. B. 4 C. D.
10.如图,在Rt△ABC中,∠ACB=90°,,点D,E分别在AB,BC上,将△BDE沿DE折叠,点B落在AC的延长线的点F处.若∠AFD=∠EFD,则的值为( )
A. 5
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.当x______时,分式有意义.
12.请写出一个同时符合下述条件的代数式______.(写出一个即可):
①是一个3次单项式;
②它的系数是一个负数.
13.学校组织研学,有三辆大巴,小明和小亮可以任选一辆,则两人坐上同一辆车的概率是______.
14.如图是铺设在人行道上地板砖的一部分,它是由正六边形和菱形镶嵌而成,A,B,C为多边形的顶点,则cos∠ABC的值为______.
15.如图,在直角坐标系中,点B在x轴上,点A,C在反比例函数的图象上,且AB=AO,BC⊥x轴,OC与AB相交于点D,若OC=1,则OD的长为______.
16.如图,在矩形ABCD中,AB=2,点P在边BC上,过点P作AP的垂线交射线CD于点Q,若有且只有三个不同的点P,使得,则BC的长为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
小明的一道习题解答过程如下:
(1)小明解答正确吗?若不正确,他是从第______步开始出错的,请你给出完整的正确计算过程.
(2)当m=1,n=-3时,求此代数式的值.
19.(本小题8分)
在某次质量抽测中,有一道分值为3分的试题(得分为整数),为了解学生此题得分情况,老师随机抽取若干名学生的抽测卷,对该题的得分进行统计,两位同学分别绘制如下两幅不完整的统计图.
(1)求图中m的值,并补全条形统计图.
(2)通过计算判断,这道题属于哪一类难度?
说明
1.难度系数k=,
2.①0.2<k≤0.4,较难题;
②0.4<k≤0.7,中档题;
③k>0.7,容易题.
20.(本小题8分)
如图是4×4的正方形网格,△ABC的三个顶点均在格点上.
(1)将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,在图1中作出△AB1C1.
(2)在图2中作格点△A2B2C2,使△A2B2C2~△ABC,且相似比为.
21.(本小题8分)
学校与家在一条笔直马路边上,兄妹两人同时出发,哥哥从家步行前往学校,到后立刻以原速原路返回家中.妹妹从学校步行回家,途中遇到哥哥后,休息一会按原速回家.如图是两人与家的距离y(米)与哥哥行走时间x(分钟)之间的函数关系如图所示.
(1)求线段AB的函数表达式.
(2)求图中点C的坐标,并说明其含义.
22.(本小题10分)
如图,在Rt△ABC中,D为斜边AB的中点,过射线CD的上点E,作CD的垂线,与CB延长线,AB,AC分别相交于点F,H,G.已知CB=CE.
(1)求证:△ABC≌△FCE.
(2)若CB=3,EF=4,求AG的长.
23.(本小题10分)
在平面直角坐标系中,二次函数y=ax2+bx+4(a≠0)的图象的对称轴为直线x=-1,且过点(2,0).
(1)求该二次函数的表达式.
(2)已知m≤x≤n.
①若m+n=4,该二次函数的最小值为,求n的值.
②若m+n<-2,有,求m的值.
24.(本小题12分)
如图,在△ABC中,AB=AC,O在AB上,以点O为圆心,OB长为半径作⊙O,与AC相切于点E,与AB,BC分别相交于点D,F,连结EF.
(1)连接OF,求证:OF∥AC.
(2)若BD=2AD,求的值.
(3)若tanB=3,求证:E为AC的中点.
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】B
11.【答案】≠1
12.【答案】-b3
13.【答案】
14.【答案】
15.【答案】0.8
16.【答案】5
17.【答案】11.
18.【答案】一;正确解答过程见解答;
216.
19.【答案】m≈28.33;图形见解析;
这道题为中档题.
20.【答案】见解答.
见解答.
21.【答案】y=-40x+1200(0≤x≤12);
(22,720),妹妹从学校出发22分钟后离家的距离为720米.
22.【答案】证明见解答过程;
.
23.【答案】该二次函数的表达式;
①3;
②-6.
24.【答案】证明见解析; ; 证明见解析.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.-5的相反数是( )
A. -5 B. 5 C. D. -
2.下列四个标志中,是轴对称图形的是( )
A. B. C. D.
3.2025年春节假期8天,全国国内出游501000000人次,数“501000000”用科学记数法可表示为( )
A. 0.501×108 B. 0.501×109 C. 5.01×108 D. 5.01×109
4.已知实数a,b满足a+b<0,若数a在数轴上对应点的位置如图所示,则数b所对应的点可以在( )
A. 线段BC上 B. 线段AB上 C. 线段CD上 D. 线段DE上
5.如图,根据尺规作图的痕迹,下列判断错误的是( )
A. 点O为AB,AC两条中垂线的交点
B. 点O到△ABC三个顶点的距离相等
C. 点O为△ABC的外接圆的圆心
D. 点O到△ABC三边的距离都相等
6.学校组织人工智能竞赛,成绩划分为A,B,C,D,E,F六个档次,小明随机抽取36名学生的竞赛成绩,并画出如图所示的统计图,若A,B为优秀,估计这次竞赛成绩的优秀率是( )
A. B. C. D.
7.为测量小河的宽度CD,小明在河两岸C,D测得大楼AB楼顶A的仰角分别为α,β.若大楼AB的高为h,则CD的长可表示为( )
A. (tanα-tanβ)h
B. (sinα-sinβ)h
C.
D.
8.如图,AB为⊙O的直径,C为弧BD的中点,弦BE∥AD,CE与AB相交于点F.若∠D=115°,则∠CFB的度数是( )
A. 50°
B. 65°
C. 75°
D. 80°
9.如图1,把边长为的正方形做成七巧板,拼成图2的轴对称图形,A,B为三角形的顶点,则AB的长为( )
A. B. 4 C. D.
10.如图,在Rt△ABC中,∠ACB=90°,,点D,E分别在AB,BC上,将△BDE沿DE折叠,点B落在AC的延长线的点F处.若∠AFD=∠EFD,则的值为( )
A. 5
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.当x______时,分式有意义.
12.请写出一个同时符合下述条件的代数式______.(写出一个即可):
①是一个3次单项式;
②它的系数是一个负数.
13.学校组织研学,有三辆大巴,小明和小亮可以任选一辆,则两人坐上同一辆车的概率是______.
14.如图是铺设在人行道上地板砖的一部分,它是由正六边形和菱形镶嵌而成,A,B,C为多边形的顶点,则cos∠ABC的值为______.
15.如图,在直角坐标系中,点B在x轴上,点A,C在反比例函数的图象上,且AB=AO,BC⊥x轴,OC与AB相交于点D,若OC=1,则OD的长为______.
16.如图,在矩形ABCD中,AB=2,点P在边BC上,过点P作AP的垂线交射线CD于点Q,若有且只有三个不同的点P,使得,则BC的长为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
小明的一道习题解答过程如下:
(1)小明解答正确吗?若不正确,他是从第______步开始出错的,请你给出完整的正确计算过程.
(2)当m=1,n=-3时,求此代数式的值.
19.(本小题8分)
在某次质量抽测中,有一道分值为3分的试题(得分为整数),为了解学生此题得分情况,老师随机抽取若干名学生的抽测卷,对该题的得分进行统计,两位同学分别绘制如下两幅不完整的统计图.
(1)求图中m的值,并补全条形统计图.
(2)通过计算判断,这道题属于哪一类难度?
说明
1.难度系数k=,
2.①0.2<k≤0.4,较难题;
②0.4<k≤0.7,中档题;
③k>0.7,容易题.
20.(本小题8分)
如图是4×4的正方形网格,△ABC的三个顶点均在格点上.
(1)将△ABC绕点A按逆时针方向旋转90°得到△AB1C1,在图1中作出△AB1C1.
(2)在图2中作格点△A2B2C2,使△A2B2C2~△ABC,且相似比为.
21.(本小题8分)
学校与家在一条笔直马路边上,兄妹两人同时出发,哥哥从家步行前往学校,到后立刻以原速原路返回家中.妹妹从学校步行回家,途中遇到哥哥后,休息一会按原速回家.如图是两人与家的距离y(米)与哥哥行走时间x(分钟)之间的函数关系如图所示.
(1)求线段AB的函数表达式.
(2)求图中点C的坐标,并说明其含义.
22.(本小题10分)
如图,在Rt△ABC中,D为斜边AB的中点,过射线CD的上点E,作CD的垂线,与CB延长线,AB,AC分别相交于点F,H,G.已知CB=CE.
(1)求证:△ABC≌△FCE.
(2)若CB=3,EF=4,求AG的长.
23.(本小题10分)
在平面直角坐标系中,二次函数y=ax2+bx+4(a≠0)的图象的对称轴为直线x=-1,且过点(2,0).
(1)求该二次函数的表达式.
(2)已知m≤x≤n.
①若m+n=4,该二次函数的最小值为,求n的值.
②若m+n<-2,有,求m的值.
24.(本小题12分)
如图,在△ABC中,AB=AC,O在AB上,以点O为圆心,OB长为半径作⊙O,与AC相切于点E,与AB,BC分别相交于点D,F,连结EF.
(1)连接OF,求证:OF∥AC.
(2)若BD=2AD,求的值.
(3)若tanB=3,求证:E为AC的中点.
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】B
11.【答案】≠1
12.【答案】-b3
13.【答案】
14.【答案】
15.【答案】0.8
16.【答案】5
17.【答案】11.
18.【答案】一;正确解答过程见解答;
216.
19.【答案】m≈28.33;图形见解析;
这道题为中档题.
20.【答案】见解答.
见解答.
21.【答案】y=-40x+1200(0≤x≤12);
(22,720),妹妹从学校出发22分钟后离家的距离为720米.
22.【答案】证明见解答过程;
.
23.【答案】该二次函数的表达式;
①3;
②-6.
24.【答案】证明见解析; ; 证明见解析.
第1页,共1页
同课章节目录
