人教A版(2019)必修第一册 4.3.2 对数的运算 课件(共41张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册 4.3.2 对数的运算 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:08:51 | ||
图片预览









文档简介
(共41张PPT)
第四章 指数函数与对数函数
对数的运算
高中数学 · 必修一
知识回顾
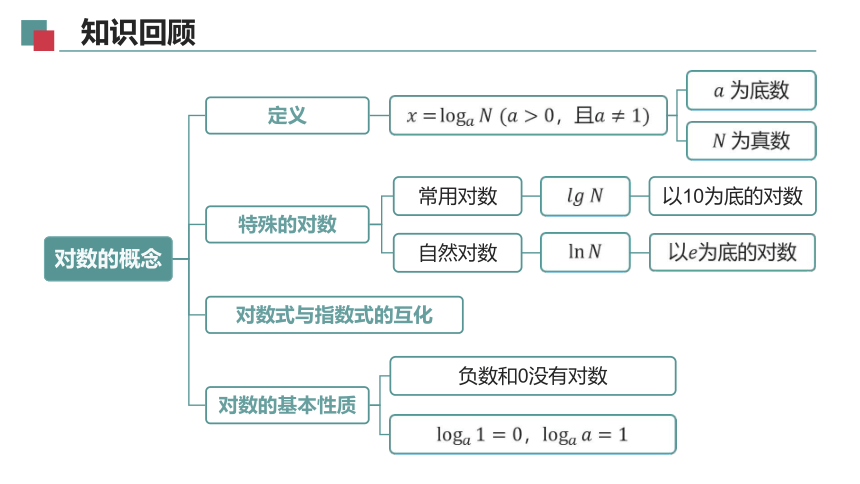
对数的概念
定义
为底数
为真数
特殊的对数
常用对数
自然对数
对数式与指数式的互化
对数的基本性质
负数和0没有对数
,
以10为底的对数
以为底的对数
知识回顾
对数式与指数式的互化:
表达形式 对应的运算
底数 指数 幂
底数 对数 真数
学习目标
理解并掌握对数的运算性质,并进行简单的计算;
理解对数换底公式,能够用公式实现其他底数的对数的运算.
核心素养
数学抽象
对数的运算性质;
逻辑推理
推导对数的运算性质和换底公式;
数学运算
对数的运算.
课程导入
知识回顾
指数幂的运算性质:
(1)
(2)
(3)
Part 01
对数的运算性质
问题探究
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
问题
问题探究
设 , .
因为 ,所以 .
根据对数与指数间的关系可得
, ,
故 .
此推导方法是从指数幂运算的角度出发,还有其他推导方法吗?
方法一
1
问题探究
设 , ,
即 , ,
所以 ,
所以 ,
故 .
此推导方法是从对数运算的角度出发.
方法二
1
问题探究
设 , ,
因为 ,所以
根据对数与指数间的关系可得
, ,
故 .
2
问题探究
设 ,
因为 ,所以 ,
所以 .
故
3
因为
对数的运算性质
对数的运算性质
(1);
(2);
(3).
如果,且,,那么
例题解析
例3
求下列各式的值:
(1); (2).
解:
(1)
(2)
例题解析
例4
用 ,, 表示 .
解:
跟踪训练
求下列各式的值:
(1); (2).
(3);
(4).
跟踪训练
【解析】
(1)
(2)
(3)
(4)
Part 02
对数换底公式
问题探究
1. 利用计算工具求 , 的近似值;
探究
问题探究
2. 根据对数的定义,你能利用, 的值求的值吗?
探究
【分析】
观察
共同点
设 ,则 ,.
所以 ,
所以 ,即
问题探究
3. 根据对数的定义,你能用,表示吗?
探究
设 ,则 ,于是
根据性质(3)得 , ,即
对数换底公式
对数换底公式
用自然语言描述:一个对数的值等于两个同底的对数的商,其中分子是真数的对数,分母是以原对数的底数为真数的对数.
意义
对数换底公式的意义在于改变对数式的底数,把不同的底数问题转化为同底数问题后求解.
保证公式中的每一个对数式都有意义.
对数换底公式
(1)
对数换底公式的推论
(2)
(3)
(4)
对数换底公式
利用计算工具,可得
在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍.
因为 ,即
应用
所以
【解析】
由此可得,大约经过7年,B地景区的游客人次就达到2001年的2倍.
跟踪训练
1、 的值为( )
A. B. C. D.
【解析】
跟踪训练
2、
(1)原式
【解析】
(1); (2).
(2)原式
例题解析
例5
尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
例题解析
解:
设里氏9.0级和8.0级地震的能量分别为和.
由 可得
于是,
利用计算工具可得,
虽然里氏9.0级地震与里氏8.0级地震仅相差1级,但前者释放出来的能量却是后者的约32倍.
例题解析
想一想,为什么两次地震的里氏震级仅差1级,而释放的能量却相差那么多呢?
问题
例题解析
地震中能量是很大的数值,进行对数运算后,其数值就变得非常小. 这其实相当于把指数幂运算中幂的结果反映在指数上.
以10为底的指数幂运算中
在以10为底的对数运算中
所以,在指数幂运算中,“指数增长”的变化非常快;在对数运算中,“对数增长”的变化就比较慢.
Part 03
小结及随堂练习
课堂小结
对数的运算性质
(1);
(2);
(3).
如果,且,,那么
课堂小结
对数换底公式
课堂小结
对数换底公式的推论
(1)
(2)
(3)
(4)
随堂练习
1、如果,那么( )
A. B.
C. D.
【解析】
由 ,可得
随堂练习
2、计算: ( )
A. B. C. D.
【解析】
原式
随堂练习
3、设 ,,则 ( )
【解析】
A. B. C. D.
∵ ,∴
∴
随堂练习
4、朗伯比尔定律是分光光度法的基本定律,是描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系,其数学表达式为 ,其中为吸光度,为透光度,为摩尔吸光系数,为吸光物质的浓度,单位为mol/L,为吸收层厚度,单位为 cm. 保持不变,当吸光物质的浓度增加为原来的两倍时,透光度由原来的变为( )
A. B. C. D.
随堂练习
由,得 ,
【解析】
所以 .
若保持不变,当吸光物质的浓度增加为原来的两倍时,
则 ,所以 ,
所以 ,所以透光度由原来的变为.
随堂练习
5、
(1);
(2);
(3).
随堂练习
(1)原式
【解析】
(2)原式
(3)原式
第四章 指数函数与对数函数
对数的运算
高中数学 · 必修一
知识回顾
对数的概念
定义
为底数
为真数
特殊的对数
常用对数
自然对数
对数式与指数式的互化
对数的基本性质
负数和0没有对数
,
以10为底的对数
以为底的对数
知识回顾
对数式与指数式的互化:
表达形式 对应的运算
底数 指数 幂
底数 对数 真数
学习目标
理解并掌握对数的运算性质,并进行简单的计算;
理解对数换底公式,能够用公式实现其他底数的对数的运算.
核心素养
数学抽象
对数的运算性质;
逻辑推理
推导对数的运算性质和换底公式;
数学运算
对数的运算.
课程导入
知识回顾
指数幂的运算性质:
(1)
(2)
(3)
Part 01
对数的运算性质
问题探究
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
问题
问题探究
设 , .
因为 ,所以 .
根据对数与指数间的关系可得
, ,
故 .
此推导方法是从指数幂运算的角度出发,还有其他推导方法吗?
方法一
1
问题探究
设 , ,
即 , ,
所以 ,
所以 ,
故 .
此推导方法是从对数运算的角度出发.
方法二
1
问题探究
设 , ,
因为 ,所以
根据对数与指数间的关系可得
, ,
故 .
2
问题探究
设 ,
因为 ,所以 ,
所以 .
故
3
因为
对数的运算性质
对数的运算性质
(1);
(2);
(3).
如果,且,,那么
例题解析
例3
求下列各式的值:
(1); (2).
解:
(1)
(2)
例题解析
例4
用 ,, 表示 .
解:
跟踪训练
求下列各式的值:
(1); (2).
(3);
(4).
跟踪训练
【解析】
(1)
(2)
(3)
(4)
Part 02
对数换底公式
问题探究
1. 利用计算工具求 , 的近似值;
探究
问题探究
2. 根据对数的定义,你能利用, 的值求的值吗?
探究
【分析】
观察
共同点
设 ,则 ,.
所以 ,
所以 ,即
问题探究
3. 根据对数的定义,你能用,表示吗?
探究
设 ,则 ,于是
根据性质(3)得 , ,即
对数换底公式
对数换底公式
用自然语言描述:一个对数的值等于两个同底的对数的商,其中分子是真数的对数,分母是以原对数的底数为真数的对数.
意义
对数换底公式的意义在于改变对数式的底数,把不同的底数问题转化为同底数问题后求解.
保证公式中的每一个对数式都有意义.
对数换底公式
(1)
对数换底公式的推论
(2)
(3)
(4)
对数换底公式
利用计算工具,可得
在4.2.1的问题1中,求经过多少年B地景区的游客人次是2001年的2倍.
因为 ,即
应用
所以
【解析】
由此可得,大约经过7年,B地景区的游客人次就达到2001年的2倍.
跟踪训练
1、 的值为( )
A. B. C. D.
【解析】
跟踪训练
2、
(1)原式
【解析】
(1); (2).
(2)原式
例题解析
例5
尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为
2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍(精确到1)?
例题解析
解:
设里氏9.0级和8.0级地震的能量分别为和.
由 可得
于是,
利用计算工具可得,
虽然里氏9.0级地震与里氏8.0级地震仅相差1级,但前者释放出来的能量却是后者的约32倍.
例题解析
想一想,为什么两次地震的里氏震级仅差1级,而释放的能量却相差那么多呢?
问题
例题解析
地震中能量是很大的数值,进行对数运算后,其数值就变得非常小. 这其实相当于把指数幂运算中幂的结果反映在指数上.
以10为底的指数幂运算中
在以10为底的对数运算中
所以,在指数幂运算中,“指数增长”的变化非常快;在对数运算中,“对数增长”的变化就比较慢.
Part 03
小结及随堂练习
课堂小结
对数的运算性质
(1);
(2);
(3).
如果,且,,那么
课堂小结
对数换底公式
课堂小结
对数换底公式的推论
(1)
(2)
(3)
(4)
随堂练习
1、如果,那么( )
A. B.
C. D.
【解析】
由 ,可得
随堂练习
2、计算: ( )
A. B. C. D.
【解析】
原式
随堂练习
3、设 ,,则 ( )
【解析】
A. B. C. D.
∵ ,∴
∴
随堂练习
4、朗伯比尔定律是分光光度法的基本定律,是描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系,其数学表达式为 ,其中为吸光度,为透光度,为摩尔吸光系数,为吸光物质的浓度,单位为mol/L,为吸收层厚度,单位为 cm. 保持不变,当吸光物质的浓度增加为原来的两倍时,透光度由原来的变为( )
A. B. C. D.
随堂练习
由,得 ,
【解析】
所以 .
若保持不变,当吸光物质的浓度增加为原来的两倍时,
则 ,所以 ,
所以 ,所以透光度由原来的变为.
随堂练习
5、
(1);
(2);
(3).
随堂练习
(1)原式
【解析】
(2)原式
(3)原式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
