人教A版(2019)选择性必修第二册 4.3 等比数列的前n项和公式 教案
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 4.3 等比数列的前n项和公式 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1016.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:16:07 | ||
图片预览


文档简介
课题:等比数列的前n项和
教材:人教A版2019年选择性必修第二册第四章第三节
内容解析 内容本质:等比数列定义的代数变形
内容解析:既是特殊函数,又是后续研究微积分问题能力的有力工具,起到承上启下的作用。
蕴含的思想方法:归纳推理,分类讨论。
育人价值:数学抽象,逻辑推理,数学建模,数学运算。
学情分析 认知基础:1.经历了探索等差数列通项公式,求和公式以及等比数列通项公式的过程,积累了特殊数列求和的研究经验。2.初步具备了从函数与方程的角度看待数列问题的思维习惯。认知困难:1.等比数列的前n项和公式导出。2.“倒序相加法”和“错位相减法”思维方法不同,容易产生知识的负迁移。
重点难点 教学重点:等比数列前n项和公式的导出及其应用。重点突出策略:“趣”设情境,激发兴趣;“巧”搭阶梯,逐步递进;“重”在思考,深入理解;“用”于生活,形成结构。
教学难点:用错位相减法推导等比数列前n项和公式。难点突破策略:1.“归纳猜想→推理论证→行程结构→应用迁移”等活动过程。 2.通过问题串层层深入。
目标达成 目标设置:1.能够导出等比数列前n项和模型。2.能够推导等比数列前n项和公式。3.能够应用公式解决简单问题。
目标达成:1.能够从情境中抽象并建立等比数列前n项的数学模型; 2.能够理解错位和相减的意义,并能够推导公式; 3.能够运用公式解决具体的,简单的问题。
教学资源 数学史短剧,中国古代诗词:激发学生学习兴趣和探究欲望。PPT教学课件。手机拍摄,实物投影:及时传输学生书写内容,丰富互动方式,激发学生的成就感。
教学组织 认知过程:猜想公式→推导公式→分析公式→应用公式——突出教学重点,突破教学难点。
学生活动:归纳猜想→推理论证→内化认知→应用迁移——认知暗线
教师活动:引导归纳→点拨释疑→补充完善→总结提升——活动明线
以本节课为载体,提炼公式课教学的一般路径,站在上号一节课的角度去体会如何上好一类课,进而上号一门课。
教学方法 问题探索法及启发式讲授法
教学过程:
一、复习回顾
回顾等比数列定义,通项公式。
(1)等比数列定义:(,
(2)等比数列通项公式:
(3)等差数列前n项和公式的推导方法:倒序相加法。
根据等差数列的定义
(1)
(2)
(1)+(2)得:
二、情境引入
阅读:课本第55页“国王赏麦的故事”:国王舍罕王,宰相达依尔(国际象棋发明者)。
问题1:如何计算(观察法,图形法)
引出课题:等比数列的前n项和。
三、问题探讨
问题2:一般化:
n 1 2 3 4 5 …… n
1 3 7 15 31 ?
问题3:首相是1,公比是q等比数列的前n项和
=?(数学猜想,特殊值检验)
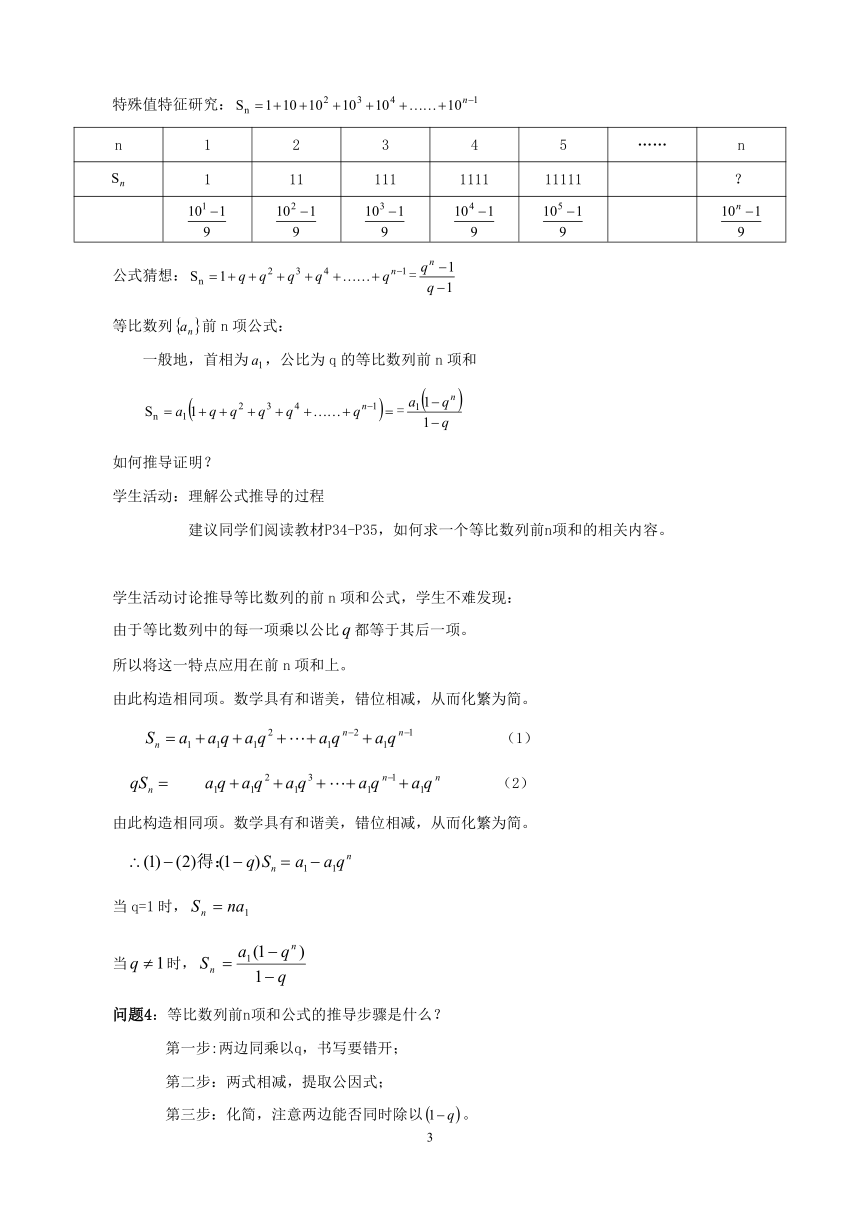
特殊值特征研究:
n 1 2 3 4 5 …… n
1 11 111 1111 11111 ?
公式猜想:=
等比数列前n项公式:
一般地,首相为,公比为q的等比数列前n项和
=
如何推导证明?
学生活动:理解公式推导的过程
建议同学们阅读教材P34-P35,如何求一个等比数列前n项和的相关内容。
学生活动讨论推导等比数列的前n项和公式,学生不难发现:
由于等比数列中的每一项乘以公比都等于其后一项。
所以将这一特点应用在前n项和上。
由此构造相同项。数学具有和谐美,错位相减,从而化繁为简。
(1)
(2)
由此构造相同项。数学具有和谐美,错位相减,从而化繁为简。
当q=1时,
当时,
问题4:等比数列前n项和公式的推导步骤是什么?
第一步:两边同乘以q,书写要错开;
第二步:两式相减,提取公因式;
第三步:化简,注意两边能否同时除以。
问题5:是不是两边只能同时乘以q,能不能乘以其他数?
方式1:两边同乘以,过程如下:
(1)
(2)
(1)-(2)可得:
方式2:两边同乘以,过程如下:
(1)
(2)
(1)-(2)可得:
选择乘以哪个数的标准:运算简洁明了。
回归情境:
以1000粒40g为标准,超过7000亿吨。
①以2023年世界粮食年产量26.28亿吨为标准,需要连续种植270年。
②全世界人口80亿计算,每人每天吃1kg为标准,可以连续吃240年。
③堆到一起,可以堆成长10米,宽8米,高从地球到太阳的距离的举行长方形柱体。
总结:指数爆炸式增长的威力。
四.对比教学
1.等差数列求和公式 倒序相加法
本质利用等差数列定义
2.等比数列求和公式 错位相减法
本质利用等比数列定义
五、例题精讲
例1.运用公式解决国王赏麦故事中的难题。
变式练习:⑴求等比数列1,2,4,8…的前多少项和是63.
⑵求等比数列1,2,4,8…第4项到第7项的和.
例2.我国明代数学家程大位所著《算术统宗》记载:
远望魏巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?
翻译:已知等比数列中,
.例3(教材P35例7).已知数列是等比数列.
总结:等比数列通项公式结合前n项和公式涉及五个量,,五个量中“知三求二”(方程思想)。
例4.已知等比数列的首项为,前n项和为,若
总结:等比数列前n项和公式中,q的分类讨论。
六、课堂小结
1、等比数列的前n项和公式:
当q=1时, (特殊情况)
当时,
2、等比数列的前n项和推导方法:错位相减法。
3、数学思想:从特殊到一,分类讨论,归纳猜想。
七、课后作业
基础题:课本P37 练习1,3,4,5
提高题:1.课本P37 练习2 2.求和
探究与发现:查阅网络,思考等比数列前n项和公式还有无其它推导方法?
八、板书设计
高斯用首尾相加法来消项
高斯
欧拉用错位相减法来消项
欧拉
4.3.2等比数列的前n项和
公式: 例1 例2
特征 例3 例4
教材:人教A版2019年选择性必修第二册第四章第三节
内容解析 内容本质:等比数列定义的代数变形
内容解析:既是特殊函数,又是后续研究微积分问题能力的有力工具,起到承上启下的作用。
蕴含的思想方法:归纳推理,分类讨论。
育人价值:数学抽象,逻辑推理,数学建模,数学运算。
学情分析 认知基础:1.经历了探索等差数列通项公式,求和公式以及等比数列通项公式的过程,积累了特殊数列求和的研究经验。2.初步具备了从函数与方程的角度看待数列问题的思维习惯。认知困难:1.等比数列的前n项和公式导出。2.“倒序相加法”和“错位相减法”思维方法不同,容易产生知识的负迁移。
重点难点 教学重点:等比数列前n项和公式的导出及其应用。重点突出策略:“趣”设情境,激发兴趣;“巧”搭阶梯,逐步递进;“重”在思考,深入理解;“用”于生活,形成结构。
教学难点:用错位相减法推导等比数列前n项和公式。难点突破策略:1.“归纳猜想→推理论证→行程结构→应用迁移”等活动过程。 2.通过问题串层层深入。
目标达成 目标设置:1.能够导出等比数列前n项和模型。2.能够推导等比数列前n项和公式。3.能够应用公式解决简单问题。
目标达成:1.能够从情境中抽象并建立等比数列前n项的数学模型; 2.能够理解错位和相减的意义,并能够推导公式; 3.能够运用公式解决具体的,简单的问题。
教学资源 数学史短剧,中国古代诗词:激发学生学习兴趣和探究欲望。PPT教学课件。手机拍摄,实物投影:及时传输学生书写内容,丰富互动方式,激发学生的成就感。
教学组织 认知过程:猜想公式→推导公式→分析公式→应用公式——突出教学重点,突破教学难点。
学生活动:归纳猜想→推理论证→内化认知→应用迁移——认知暗线
教师活动:引导归纳→点拨释疑→补充完善→总结提升——活动明线
以本节课为载体,提炼公式课教学的一般路径,站在上号一节课的角度去体会如何上好一类课,进而上号一门课。
教学方法 问题探索法及启发式讲授法
教学过程:
一、复习回顾
回顾等比数列定义,通项公式。
(1)等比数列定义:(,
(2)等比数列通项公式:
(3)等差数列前n项和公式的推导方法:倒序相加法。
根据等差数列的定义
(1)
(2)
(1)+(2)得:
二、情境引入
阅读:课本第55页“国王赏麦的故事”:国王舍罕王,宰相达依尔(国际象棋发明者)。
问题1:如何计算(观察法,图形法)
引出课题:等比数列的前n项和。
三、问题探讨
问题2:一般化:
n 1 2 3 4 5 …… n
1 3 7 15 31 ?
问题3:首相是1,公比是q等比数列的前n项和
=?(数学猜想,特殊值检验)
特殊值特征研究:
n 1 2 3 4 5 …… n
1 11 111 1111 11111 ?
公式猜想:=
等比数列前n项公式:
一般地,首相为,公比为q的等比数列前n项和
=
如何推导证明?
学生活动:理解公式推导的过程
建议同学们阅读教材P34-P35,如何求一个等比数列前n项和的相关内容。
学生活动讨论推导等比数列的前n项和公式,学生不难发现:
由于等比数列中的每一项乘以公比都等于其后一项。
所以将这一特点应用在前n项和上。
由此构造相同项。数学具有和谐美,错位相减,从而化繁为简。
(1)
(2)
由此构造相同项。数学具有和谐美,错位相减,从而化繁为简。
当q=1时,
当时,
问题4:等比数列前n项和公式的推导步骤是什么?
第一步:两边同乘以q,书写要错开;
第二步:两式相减,提取公因式;
第三步:化简,注意两边能否同时除以。
问题5:是不是两边只能同时乘以q,能不能乘以其他数?
方式1:两边同乘以,过程如下:
(1)
(2)
(1)-(2)可得:
方式2:两边同乘以,过程如下:
(1)
(2)
(1)-(2)可得:
选择乘以哪个数的标准:运算简洁明了。
回归情境:
以1000粒40g为标准,超过7000亿吨。
①以2023年世界粮食年产量26.28亿吨为标准,需要连续种植270年。
②全世界人口80亿计算,每人每天吃1kg为标准,可以连续吃240年。
③堆到一起,可以堆成长10米,宽8米,高从地球到太阳的距离的举行长方形柱体。
总结:指数爆炸式增长的威力。
四.对比教学
1.等差数列求和公式 倒序相加法
本质利用等差数列定义
2.等比数列求和公式 错位相减法
本质利用等比数列定义
五、例题精讲
例1.运用公式解决国王赏麦故事中的难题。
变式练习:⑴求等比数列1,2,4,8…的前多少项和是63.
⑵求等比数列1,2,4,8…第4项到第7项的和.
例2.我国明代数学家程大位所著《算术统宗》记载:
远望魏巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?
翻译:已知等比数列中,
.例3(教材P35例7).已知数列是等比数列.
总结:等比数列通项公式结合前n项和公式涉及五个量,,五个量中“知三求二”(方程思想)。
例4.已知等比数列的首项为,前n项和为,若
总结:等比数列前n项和公式中,q的分类讨论。
六、课堂小结
1、等比数列的前n项和公式:
当q=1时, (特殊情况)
当时,
2、等比数列的前n项和推导方法:错位相减法。
3、数学思想:从特殊到一,分类讨论,归纳猜想。
七、课后作业
基础题:课本P37 练习1,3,4,5
提高题:1.课本P37 练习2 2.求和
探究与发现:查阅网络,思考等比数列前n项和公式还有无其它推导方法?
八、板书设计
高斯用首尾相加法来消项
高斯
欧拉用错位相减法来消项
欧拉
4.3.2等比数列的前n项和
公式: 例1 例2
特征 例3 例4
