人教A版(2019)选择性必修第三册 8.1.1 变量的相关关系 课件(共23张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 8.1.1 变量的相关关系 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:19:46 | ||
图片预览






文档简介
(共23张PPT)
8.1.1变量的相关关系
我们知道,如果变量是变量的函数,那么由就能唯一确定,和这两个变量是确定的函数关系.然而,生活中的变量关系都是函数关系吗?如果不是,又该如何刻画这些变量之间的关系呢?
一 共性归纳,形成概念
问题1 试判断每组变量之间的关系是否是函数关系?并说明理由.
(1)正方形的面积S与正方形的边长a;
(2)球的体积V与球的半径R;
(3)子女身高y与父亲身高x ;
(4)商品销售收入y与广告支出x ;
(5)空气污染指数y与汽车保有量x ;
(6)粮食亩产量y与施肥量x .
关系确定,函数关系
有关系,但关系不确定
一 共性归纳,形成概念
第1组:一般来说,父亲的个子高,其子女的个子也会比较高;父亲的个子矮,其子女的个子也会比较矮。但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高。
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
一 共性归纳,形成概念
追问 相关关系在生活中有很多,你能举出一些生活中具有相关关系的例子吗?你是根据什么举出例子来的呢?
二 问题讨论,找寻方法
对两个变量之间是否具有相关关系,刚才我们是凭借经验做出的判断.生活中积累的经验的确可以在做决策时为我们提供一定的依据。但是凭经验判断一定合理吗?
二 问题讨论,找寻方法
问题2 小李说:“我的几个邻居大妈都是随着岁数增加越来越胖,我认为人体的脂肪含量随着年龄的增长越来越高.”小华却说:“不一定,我家人是越老越瘦,我认为人体的脂肪含量与年龄的增长无关.”你同意他们的说法吗 为什么?
答:两人的说法都缺乏说服力,一是样本不具有代表性,二是相关关系是一种统计关系,不一定是因果关系。小李、小华凭自己的经验进行主观判断,由于经验不同,形成的结论不同,说明凭经验判断变量间的关系有局限性,另,现实社会中也不是所有的情形都可有经验可循。所以要客观、理性的判断变量间的关系,还需要借助统计的方法,用数据来说话。
追问1 在必修课程统计内容中处理单变量数据的方法是什么?体现的基本数学思想是什么?
二 问题讨论,找寻方法
获取样本数据
表达数据
对数据定性分析
构建数字特征定量刻画数据
决策判断
追问2 类比单变量数据的研究经验,怎样才能理性、客观的判断人体脂肪含量与年龄这两个变量间的关系呢?
二 问题讨论,找寻方法
收集成对样本数据
用图表来表示成对数据
定性分析和定量分析数据
得出结论或决策
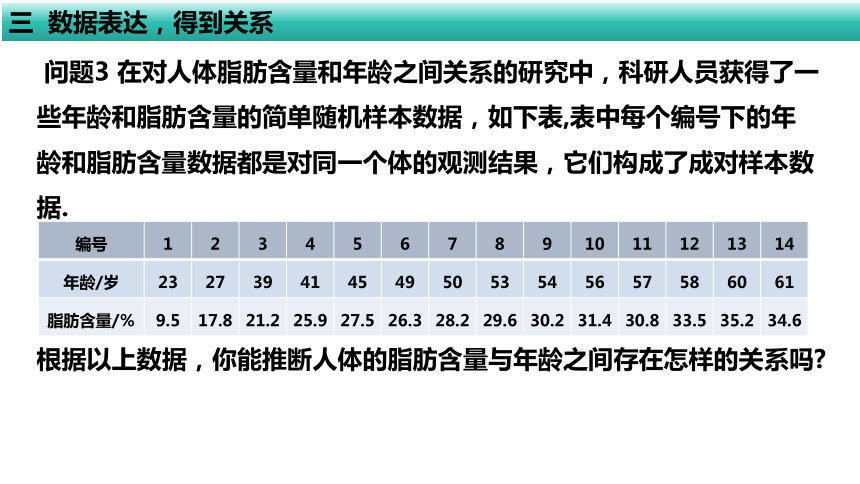
问题3 在对人体脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如下表,表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对样本数据.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗
三 数据表达,得到关系
追问1 怎样对成对样本数据进行直观的图形表达?
三 数据表达,得到关系
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗
答:从表格中初步发现年龄越大,脂肪含量越高,是相关关系。利用表格判断相关关系的缺点:趋势不直观,数据多易眼花,可借助研究单变量样本数据的经验,用类似直方图、折线图的方式,让数据表达的关系更加直观和可视化。
答:可利用直角坐标系,以x轴表示年龄,y轴表示脂肪含量,在坐标平面内描出成对样本数据对应的点构成的图。
20
25
30
35
40
45
50
55
60
65
年龄/岁
脂肪含量/%
0
5
10
15
20
25
30
35
40
●
●
●
●
●
●
●
●
●
●
●
●
●
●
15
把成对样本数据用直角坐标系中的点表示出来,这些点组成的统计图叫做散点图.
三 数据表达,得到关系
追问2 你能根据散点图的分布规律,确定年龄与人体脂肪之间存在相关关系吗?这种相关关系有什么特点?
答:散点图的分布规律:大致落在一条从左下角到右上角的直线附近,表示随年龄增大相应的脂肪含量也呈现增高的趋势,即这两个量有一起增加的关联关系,但是又不是精确的函数关系,由此可以推断它们之间具有相关关系。
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势。我们就称这两个变量正相关。反之当一个变量的值增加时,另一个变量的相应值呈现减少的趋势。我们就称这两个变量负相关。
三 数据表达,得到关系
追问3 借助右图正相关散点图思考:(1)两个变量负相关时,成对样本数据的散点图会有什么特点?
(2)你能举出生活中两个变量正相关或负相关的一些例子吗?
20
25
30
35
40
45
50
55
60
65
年龄/岁
脂肪含量/%
0
5
10
15
20
25
30
35
40
●
●
●
●
●
●
●
●
●
●
●
●
●
●
15
三 数据表达,得到关系
答:(1)散点大致落在从左上角到右下角的直线附近
(2)海拔沸点和海拔高度,商品的需求和价格等
四 图形分析,刻画类型
问题4 观察下图中三幅散点图的分布规律和特点,判断图中两个变量是否相关,是正相关还是负相关?
答:图(1)中的散点落在某条曲线附近,而不是落在一条直线附近。
图(2)中的散点落在一条折线附近,
很明显,图(1)(2)中的两个变量是相关关系,但不是正相关,也不是负相关.
图(3)中的散点杂乱无章,无规律可言,看不出两个变量有什么相关性.
追问1 结合下面4幅图,你能对两个变量的关系的类型进行分类总结吗?
四 图形分析,刻画类型
一般的,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关。如果两个变量具有相关性,但不是线性相关,我们就称这两个变量非线性相关或曲线相关。
四 图形分析,刻画类型
因此,两个变量之间的关系类型可用下图表示。
五 例题练习,巩固理解
例1 下表给出了一些地区的鸟的种类数与该地区的海拔高度的数据,鸟的种类数与海拔高度是否存在相关关系 如果是,那么这种相关关系有什么特点
地区 A B C D E F G H I J K
海拔高度/m 1250 1158 1067 457 701 731 610 670 1493 762 549
鸟的种类/种 36 30 37 11 11 13 17 13 29 4 15
解:画鸟的种类数与海拔高度的散点图,如图所示.
5
10
海拔高度/m
20
1600
1400
1200
600
0
200
400
800
1000
15
40
35
30
25
鸟的种类/种
从散点图中散点的分布看,鸟的种类数与海拔高度正相关,鸟的种类数在海拔高度1000m以上的明显多于在海拔高度1000m以下的. 但从局部看,不管是在海拔高度1000m以上,还是在海拔高度1000m以下,鸟的种类数和海拔高度正相关都不明显.
练习1 根据下面的散点图,推断图中的两个变量是否存在相关关系.
√
√
√
正相关
非线性相关
负相关
看不出有相关关系
五 例题练习,巩固理解
练习2 (多选)在下列各图中,每个图中的两个变量具有相关关系的是( )
√
√
五 例题练习,巩固理解
问题5 回顾本节课所学内容,并回答下列问题:
(1)为什么要研究两个变量间的相关关系?
(2)相关关系的定义和特点是什么?
(3)研究两个变量相关关系的思路是什么?和前面研究单个数据变量的基本思想一样吗?
(4)什么是散点图?散点图有什么优势和弊端?
(5)两个变量的相关关系有哪些?分别有什么特点?
六 归纳小结,巩固知识
作业1 教科书第103~104习题8.1第1、4
作业2 预习8.1.2,并思考如何定量刻画有相关关系的两个变量的相关程度.
七 布置作业,目标迁移
向月亮出发,即使不能到达,也要站在群星之中。
谢谢大家
8.1.1变量的相关关系
我们知道,如果变量是变量的函数,那么由就能唯一确定,和这两个变量是确定的函数关系.然而,生活中的变量关系都是函数关系吗?如果不是,又该如何刻画这些变量之间的关系呢?
一 共性归纳,形成概念
问题1 试判断每组变量之间的关系是否是函数关系?并说明理由.
(1)正方形的面积S与正方形的边长a;
(2)球的体积V与球的半径R;
(3)子女身高y与父亲身高x ;
(4)商品销售收入y与广告支出x ;
(5)空气污染指数y与汽车保有量x ;
(6)粮食亩产量y与施肥量x .
关系确定,函数关系
有关系,但关系不确定
一 共性归纳,形成概念
第1组:一般来说,父亲的个子高,其子女的个子也会比较高;父亲的个子矮,其子女的个子也会比较矮。但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高。
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
一 共性归纳,形成概念
追问 相关关系在生活中有很多,你能举出一些生活中具有相关关系的例子吗?你是根据什么举出例子来的呢?
二 问题讨论,找寻方法
对两个变量之间是否具有相关关系,刚才我们是凭借经验做出的判断.生活中积累的经验的确可以在做决策时为我们提供一定的依据。但是凭经验判断一定合理吗?
二 问题讨论,找寻方法
问题2 小李说:“我的几个邻居大妈都是随着岁数增加越来越胖,我认为人体的脂肪含量随着年龄的增长越来越高.”小华却说:“不一定,我家人是越老越瘦,我认为人体的脂肪含量与年龄的增长无关.”你同意他们的说法吗 为什么?
答:两人的说法都缺乏说服力,一是样本不具有代表性,二是相关关系是一种统计关系,不一定是因果关系。小李、小华凭自己的经验进行主观判断,由于经验不同,形成的结论不同,说明凭经验判断变量间的关系有局限性,另,现实社会中也不是所有的情形都可有经验可循。所以要客观、理性的判断变量间的关系,还需要借助统计的方法,用数据来说话。
追问1 在必修课程统计内容中处理单变量数据的方法是什么?体现的基本数学思想是什么?
二 问题讨论,找寻方法
获取样本数据
表达数据
对数据定性分析
构建数字特征定量刻画数据
决策判断
追问2 类比单变量数据的研究经验,怎样才能理性、客观的判断人体脂肪含量与年龄这两个变量间的关系呢?
二 问题讨论,找寻方法
收集成对样本数据
用图表来表示成对数据
定性分析和定量分析数据
得出结论或决策
问题3 在对人体脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如下表,表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对样本数据.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗
三 数据表达,得到关系
追问1 怎样对成对样本数据进行直观的图形表达?
三 数据表达,得到关系
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗
答:从表格中初步发现年龄越大,脂肪含量越高,是相关关系。利用表格判断相关关系的缺点:趋势不直观,数据多易眼花,可借助研究单变量样本数据的经验,用类似直方图、折线图的方式,让数据表达的关系更加直观和可视化。
答:可利用直角坐标系,以x轴表示年龄,y轴表示脂肪含量,在坐标平面内描出成对样本数据对应的点构成的图。
20
25
30
35
40
45
50
55
60
65
年龄/岁
脂肪含量/%
0
5
10
15
20
25
30
35
40
●
●
●
●
●
●
●
●
●
●
●
●
●
●
15
把成对样本数据用直角坐标系中的点表示出来,这些点组成的统计图叫做散点图.
三 数据表达,得到关系
追问2 你能根据散点图的分布规律,确定年龄与人体脂肪之间存在相关关系吗?这种相关关系有什么特点?
答:散点图的分布规律:大致落在一条从左下角到右上角的直线附近,表示随年龄增大相应的脂肪含量也呈现增高的趋势,即这两个量有一起增加的关联关系,但是又不是精确的函数关系,由此可以推断它们之间具有相关关系。
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势。我们就称这两个变量正相关。反之当一个变量的值增加时,另一个变量的相应值呈现减少的趋势。我们就称这两个变量负相关。
三 数据表达,得到关系
追问3 借助右图正相关散点图思考:(1)两个变量负相关时,成对样本数据的散点图会有什么特点?
(2)你能举出生活中两个变量正相关或负相关的一些例子吗?
20
25
30
35
40
45
50
55
60
65
年龄/岁
脂肪含量/%
0
5
10
15
20
25
30
35
40
●
●
●
●
●
●
●
●
●
●
●
●
●
●
15
三 数据表达,得到关系
答:(1)散点大致落在从左上角到右下角的直线附近
(2)海拔沸点和海拔高度,商品的需求和价格等
四 图形分析,刻画类型
问题4 观察下图中三幅散点图的分布规律和特点,判断图中两个变量是否相关,是正相关还是负相关?
答:图(1)中的散点落在某条曲线附近,而不是落在一条直线附近。
图(2)中的散点落在一条折线附近,
很明显,图(1)(2)中的两个变量是相关关系,但不是正相关,也不是负相关.
图(3)中的散点杂乱无章,无规律可言,看不出两个变量有什么相关性.
追问1 结合下面4幅图,你能对两个变量的关系的类型进行分类总结吗?
四 图形分析,刻画类型
一般的,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关。如果两个变量具有相关性,但不是线性相关,我们就称这两个变量非线性相关或曲线相关。
四 图形分析,刻画类型
因此,两个变量之间的关系类型可用下图表示。
五 例题练习,巩固理解
例1 下表给出了一些地区的鸟的种类数与该地区的海拔高度的数据,鸟的种类数与海拔高度是否存在相关关系 如果是,那么这种相关关系有什么特点
地区 A B C D E F G H I J K
海拔高度/m 1250 1158 1067 457 701 731 610 670 1493 762 549
鸟的种类/种 36 30 37 11 11 13 17 13 29 4 15
解:画鸟的种类数与海拔高度的散点图,如图所示.
5
10
海拔高度/m
20
1600
1400
1200
600
0
200
400
800
1000
15
40
35
30
25
鸟的种类/种
从散点图中散点的分布看,鸟的种类数与海拔高度正相关,鸟的种类数在海拔高度1000m以上的明显多于在海拔高度1000m以下的. 但从局部看,不管是在海拔高度1000m以上,还是在海拔高度1000m以下,鸟的种类数和海拔高度正相关都不明显.
练习1 根据下面的散点图,推断图中的两个变量是否存在相关关系.
√
√
√
正相关
非线性相关
负相关
看不出有相关关系
五 例题练习,巩固理解
练习2 (多选)在下列各图中,每个图中的两个变量具有相关关系的是( )
√
√
五 例题练习,巩固理解
问题5 回顾本节课所学内容,并回答下列问题:
(1)为什么要研究两个变量间的相关关系?
(2)相关关系的定义和特点是什么?
(3)研究两个变量相关关系的思路是什么?和前面研究单个数据变量的基本思想一样吗?
(4)什么是散点图?散点图有什么优势和弊端?
(5)两个变量的相关关系有哪些?分别有什么特点?
六 归纳小结,巩固知识
作业1 教科书第103~104习题8.1第1、4
作业2 预习8.1.2,并思考如何定量刻画有相关关系的两个变量的相关程度.
七 布置作业,目标迁移
向月亮出发,即使不能到达,也要站在群星之中。
谢谢大家
