人教A版(2019)选择性必修第三册 8.2.3 一元线性回归模型的应用 课件(共19张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 8.2.3 一元线性回归模型的应用 课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:21:16 | ||
图片预览

文档简介
(共19张PPT)
8.2.3一元线性回归模型的应用
经验表明,对于同一树种,一般树的胸径越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据如下表所示,试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3
树高/m 18.8 19.2 21.0 21.0 22.1 22.1
编号 7 8 9 10 11 12
胸径/cm 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 22.4 22.6 23.0 24.3 23.9 24.7
提出问题1
解释变量:
响应变量:
杭州市高中数学青年教师核心组
明确变量,
画散点图
胸径
树高
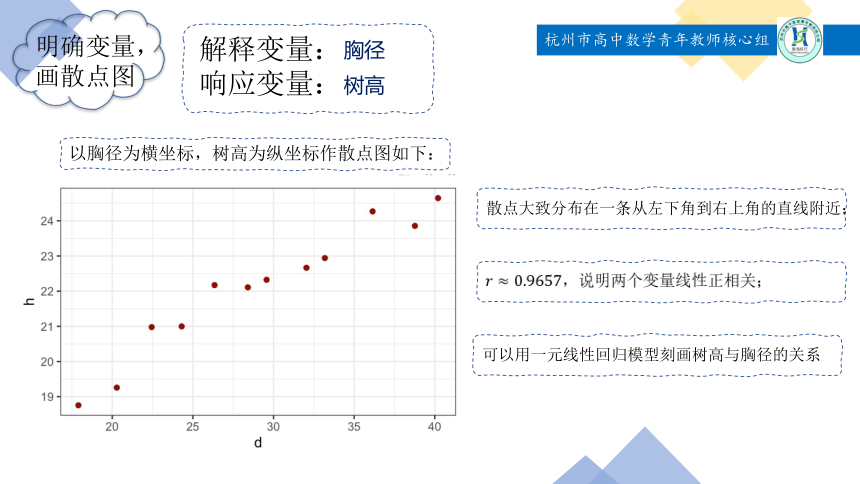
以胸径为横坐标,树高为纵坐标作散点图如下:
散点大致分布在一条从左下角到右上角的直线附近;
,说明两个变量线性正相关;
可以用一元线性回归模型刻画树高与胸径的关系
杭州市高中数学青年教师核心组
确定模型,
求解参数
胸径:d
树高:h
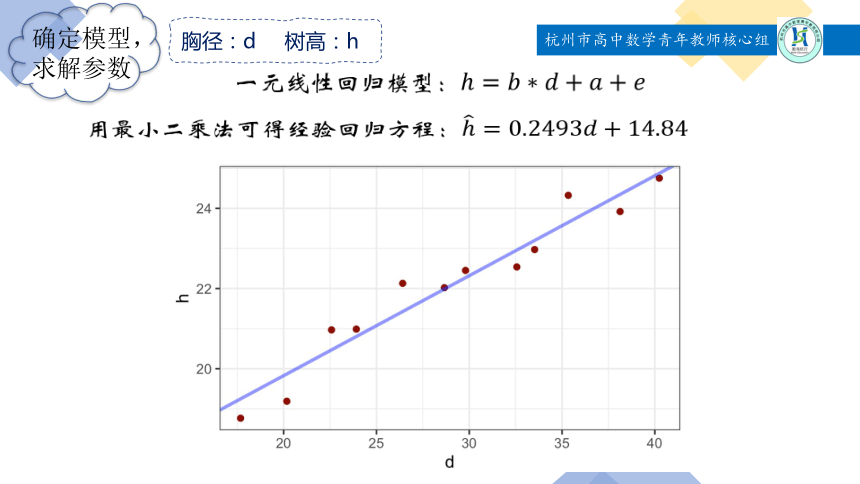
一元线性回归模型:
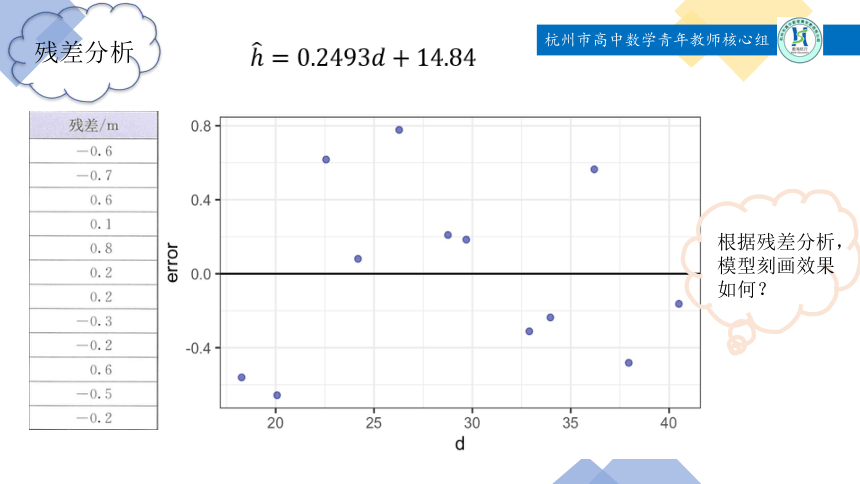
用最小二乘法可得经验回归方程:
杭州市高中数学青年教师核心组
残差分析
根据残差分析,模型刻画效果如何?
杭州市高中数学青年教师核心组
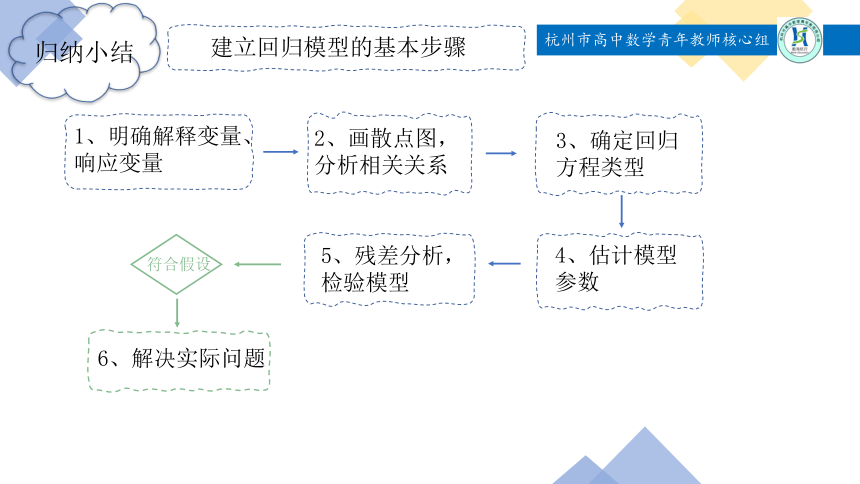
归纳小结
建立回归模型的基本步骤
1、明确解释变量、响应变量
2、画散点图,分析相关关系
3、确定回归方程类型
4、估计模型参数
5、残差分析,检验模型
符合假设
6、解决实际问题
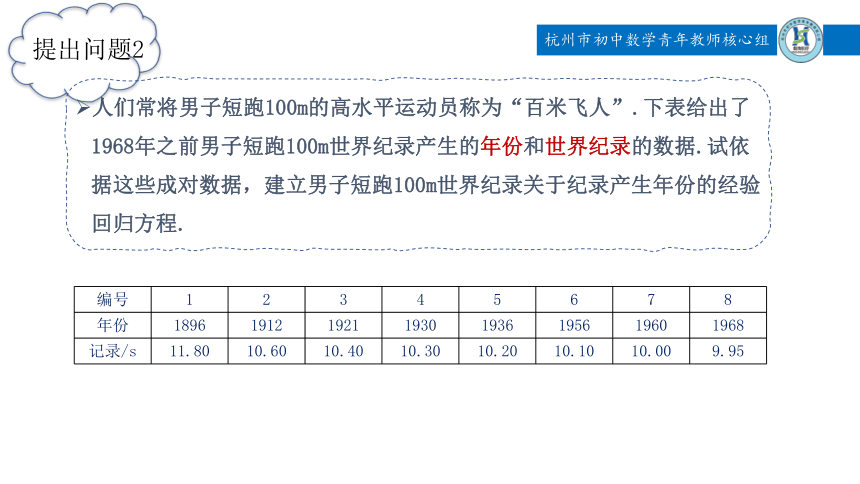
人们常将男子短跑100m的高水平运动员称为“百米飞人”.下表给出了1968年之前男子短跑100m世界纪录产生的年份和世界纪录的数据.试依据这些成对数据,建立男子短跑100m世界纪录关于纪录产生年份的经验回归方程.
提出问题2
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
解释变量:
响应变量:
杭州市高中数学青年教师核心组
明确变量,
画散点图
年份
世界纪录
以年份为横坐标,世界纪录为纵坐标作散点图如下:
散点大致分布在一条从左上角到右下角的直线附近;
,说明两个变量线性负相关;
似乎可以用一元线性回归模型刻画
杭州市高中数学青年教师核心组
确定模型,
求解参数
年份:t
纪录:Y
一元线性回归模型:
用最小二乘法可得经验回归方程:
回归直线对散点的拟合效果好吗?
杭州市高中数学青年教师核心组
残差分析
根据残差分析,模型刻画效果如何?
杭州市高中数学青年教师核心组
修改模型
年份:t
纪录:Y
散点的分布呈现非线性特征:中间下凸且递减的曲线
杭州市高中数学青年教师核心组
修改模型
年份:t
纪录:Y
注意到100m短跑的第一个世界纪录产生于1896年,可以怎样构造该对数型函数?
经过怎样的变换就可以转化成线性方程?
令 ,则有
杭州市高中数学青年教师核心组
修改模型
年份:
纪录:
散点的分布呈现出很强的线性特征;
,;可以建立一元线性回归模型
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法一:
直接观察法
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法二:
残差分析
残差平方和越小,说明模型拟合效果越好
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法三:
比较
(决定系数)
越大,说明残差平方和越小,模型拟合效果越好
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法四:
用新数据
检验模型
杭州市高中数学青年教师核心组
归纳小结
建立回归模型的基本步骤
1、明确解释变量、响应变量
2、画散点图,分析相关关系
3、确定回归方程类型
4、估计模型参数
5、残差分析,检验模型
符合假设
6、解决实际问题
线性模型
非线性模型
转换
不符合假设
杭州市高中数学青年教师核心组
总结反思
使用经验回归方程的注意事项:
1、经验回归方程只适用于所研究的样本的总体;
2、经验回归方程一般都有时效性;
3、解释变量的取值不能离样本数据的范围太远;
4、不能期望经验回归方程得到的预报值就是响应变量的精确值
8.2.3一元线性回归模型的应用
经验表明,对于同一树种,一般树的胸径越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据如下表所示,试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3
树高/m 18.8 19.2 21.0 21.0 22.1 22.1
编号 7 8 9 10 11 12
胸径/cm 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 22.4 22.6 23.0 24.3 23.9 24.7
提出问题1
解释变量:
响应变量:
杭州市高中数学青年教师核心组
明确变量,
画散点图
胸径
树高
以胸径为横坐标,树高为纵坐标作散点图如下:
散点大致分布在一条从左下角到右上角的直线附近;
,说明两个变量线性正相关;
可以用一元线性回归模型刻画树高与胸径的关系
杭州市高中数学青年教师核心组
确定模型,
求解参数
胸径:d
树高:h
一元线性回归模型:
用最小二乘法可得经验回归方程:
杭州市高中数学青年教师核心组
残差分析
根据残差分析,模型刻画效果如何?
杭州市高中数学青年教师核心组
归纳小结
建立回归模型的基本步骤
1、明确解释变量、响应变量
2、画散点图,分析相关关系
3、确定回归方程类型
4、估计模型参数
5、残差分析,检验模型
符合假设
6、解决实际问题
人们常将男子短跑100m的高水平运动员称为“百米飞人”.下表给出了1968年之前男子短跑100m世界纪录产生的年份和世界纪录的数据.试依据这些成对数据,建立男子短跑100m世界纪录关于纪录产生年份的经验回归方程.
提出问题2
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
解释变量:
响应变量:
杭州市高中数学青年教师核心组
明确变量,
画散点图
年份
世界纪录
以年份为横坐标,世界纪录为纵坐标作散点图如下:
散点大致分布在一条从左上角到右下角的直线附近;
,说明两个变量线性负相关;
似乎可以用一元线性回归模型刻画
杭州市高中数学青年教师核心组
确定模型,
求解参数
年份:t
纪录:Y
一元线性回归模型:
用最小二乘法可得经验回归方程:
回归直线对散点的拟合效果好吗?
杭州市高中数学青年教师核心组
残差分析
根据残差分析,模型刻画效果如何?
杭州市高中数学青年教师核心组
修改模型
年份:t
纪录:Y
散点的分布呈现非线性特征:中间下凸且递减的曲线
杭州市高中数学青年教师核心组
修改模型
年份:t
纪录:Y
注意到100m短跑的第一个世界纪录产生于1896年,可以怎样构造该对数型函数?
经过怎样的变换就可以转化成线性方程?
令 ,则有
杭州市高中数学青年教师核心组
修改模型
年份:
纪录:
散点的分布呈现出很强的线性特征;
,;可以建立一元线性回归模型
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法一:
直接观察法
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法二:
残差分析
残差平方和越小,说明模型拟合效果越好
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法三:
比较
(决定系数)
越大,说明残差平方和越小,模型拟合效果越好
杭州市高中数学青年教师核心组
对比模型
模型(1):
模型(2):
方法四:
用新数据
检验模型
杭州市高中数学青年教师核心组
归纳小结
建立回归模型的基本步骤
1、明确解释变量、响应变量
2、画散点图,分析相关关系
3、确定回归方程类型
4、估计模型参数
5、残差分析,检验模型
符合假设
6、解决实际问题
线性模型
非线性模型
转换
不符合假设
杭州市高中数学青年教师核心组
总结反思
使用经验回归方程的注意事项:
1、经验回归方程只适用于所研究的样本的总体;
2、经验回归方程一般都有时效性;
3、解释变量的取值不能离样本数据的范围太远;
4、不能期望经验回归方程得到的预报值就是响应变量的精确值
