人教A版(2019)高中数学选择性必修第三册第八章 成对数据的统计分析 复习课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册第八章 成对数据的统计分析 复习课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 553.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 22:43:05 | ||
图片预览







文档简介
(共25张PPT)
第八章 成对数据的统计分析
学习目标
1. 理解正相关、负相关、线性相关的概念;掌握样本相关系数的公式,能利用样本相关系数描述成对样本数据的数字特征。
2.通过具体案例理解一元线性回归模型、经验回归方程,以及一元线性回归模型中参数的最小二乘估计。
3.掌握决定系数的公式,并能利用决定系数判断不同模型拟合的效果。
4.掌握列联表和独立性检验的概念,并能通过列联表和独立性检验解决基本的实际问题。
8.1 成对数据的统计相关性
引言
频率分布直方图描述样本数据的分布规律,均值刻画样本数据的击中趋势,用方差刻画样本数据的离散程度,这些方法适用于通过样本认识单个变量的统计规律。
在现实中,我们经常需要了解两个或两个以上变量之间的关系,例如教育部门为掌握学生身体健康状况,需要了解身高变量和体重变量之间的关系;医疗部门要制定预防青少年近视的措施,需要了解有哪儿些因素会影响视力,以及这些因素是如何影响视力的;商家要根据顾客的意见改进服务水平,希望了解哪儿些因素影响服务水平,以及这些因素是如何起作用的。为此我们需要进一步通过样本推断变量之间关系的知识和方法。
8.1.1 变量的相关关系
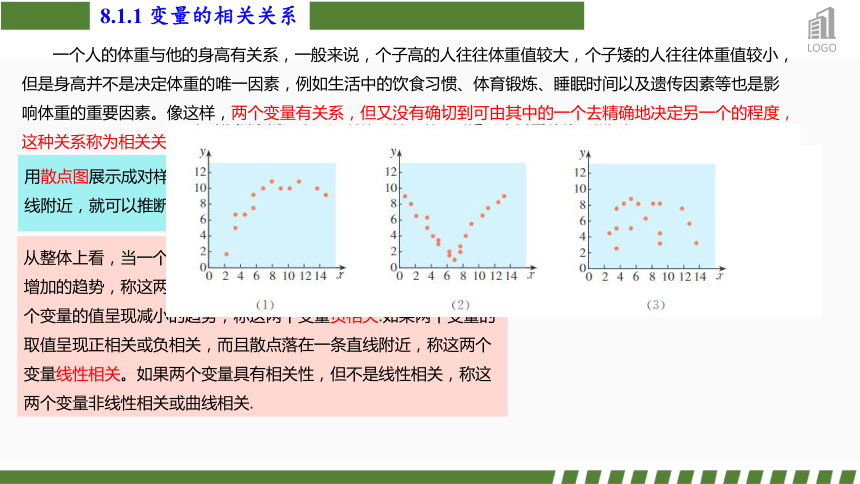
一个人的体重与他的身高有关系,一般来说,个子高的人往往体重值较大,个子矮的人往往体重值较小,但是身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素。像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系。
用散点图展示成对样本数据的变化特征,图中散点大致落在一条直线附近,就可以推断两个变量之间存在着相关关系。
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,称这两个变量正相关;当一个变量的值增加时,另一个变量的值呈现减小的趋势,称这两个变量负相关.如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,称这两个变量线性相关。如果两个变量具有相关性,但不是线性相关,称这两个变量非线性相关或曲线相关.
8.1.2 样本相关系数
散点图虽然能直观地看出两个变量是否存在相关关系,但无法确切地反映成对样本数据的相关程度,我们需要引入样本相关系数r来量化两个变量之间的相关程度的大小。
典例解析
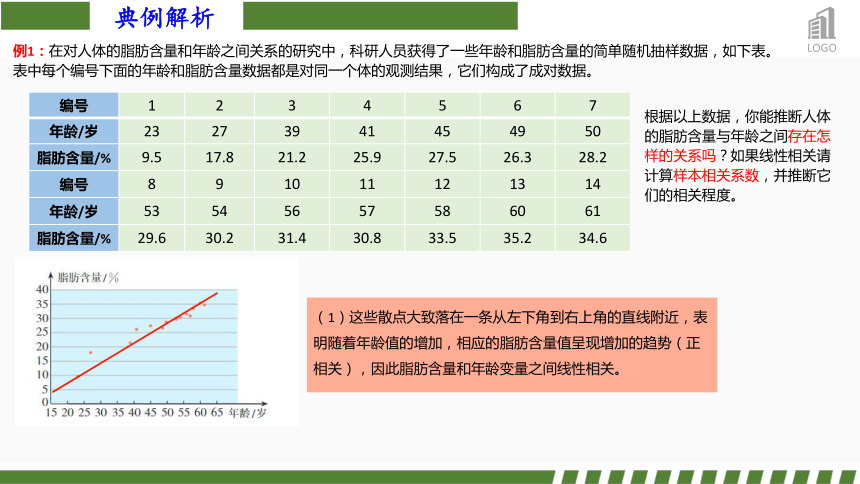
例1:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机抽样数据,如下表。表中每个编号下面的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据。
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?如果线性相关请计算样本相关系数,并推断它们的相关程度。
(1)这些散点大致落在一条从左下角到右上角的直线附近,表明随着年龄值的增加,相应的脂肪含量值呈现增加的趋势(正相关),因此脂肪含量和年龄变量之间线性相关。
典例分析
8.2 一元线性回归模型及其应用
8.2.1 一元线性回归模型
通过前面的学习,我们已经学会推断两个变量是否存在相关关系以及相关程度的大小。如果能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系,那么我们可以利用这两个模型研究两个变量之间的随机关系,并通过模型进行预测.
例2:生活经验告诉我们,儿子的身高与父亲的身高不仅线性相关,而且正相关,即父亲的身高较高时,儿子的身高通常也比较高。为了进一步研究两者之间的关系,有人调查了某所高校14名男大学生的身高及其父亲的身高,得到的数据如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
根据题意可得,儿子身高和父亲身高线性相关,且r≈0.886,相关程度较高
思考:儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
由此可见,儿子身高和父亲身高之间不是函数关系,也就不能用函数模型刻画。
散点大致分布在一条直线附近,表明儿子身高和父亲身高这两个变量之间有较强的线性相关关系,因此可以用一次函数来刻画父亲身高对儿子身高的影响,而把影响儿子身高的其他因素,如目前身高、生活环境、饮食习惯等作为误差,得到刻画两个变量之间关系的线性回归模型,其中随机误差是一个随机变量.
概念生成
8.2.2 一元线性回归模型参数的最小二乘估计
8.2.2 一元线性回归模型参数的最小二乘估计
残差比较均匀地分布在横轴(x=0)的两侧,
说明该模型满足一元线性回归模型的假设。
典例分析
例3:人们将男子短跑100m的高水平运动员称为“百米飞人”。下表给出1968年之前男子短跑100m世界纪录产生的年份
和世界记录的数据。试根据这些成对数据,建立男子短跑100m世界纪录关于记录产生年份的经验回归方程。
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
以成对数据中的世界纪录产生年份为生坐标,世界纪录为纵坐标作散点图,得到右图.
散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程。
典例分析
8.3 列联表与独立性检验
8.3.1 分类变量与列联表
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题,例如:就读不同学校是否对学生的成绩有影响;不同班级学生用于体育锻炼的时间是否有差别;吸烟是否会增加患肺癌的风险等等.
在讨论上述问题时,为了方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量。分类变量的取值可以用实数表示,例如:学生所在的班级可以用1,2,3表示;男性,女性可以用1,0表示等等。在很多时候,这些数值只作为编号使用,并没有通常的大小和现实意义。本节我们主要讨论取值{0,1}的分类变量的关联性问题。
例4:为了有针对性提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查,数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻炼。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
为了清晰,我们用表格整理数据,如下:
性别 锻炼
合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
2×2列联表
8.3.2 独立性检验
前面我们通过列联表整理成对分类变量的样本观测数据,并根据随机事件频率的稳定性推断两个分类变量之间是否有关联。对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误概率可能性会较大。因此需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
X Y
合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
概念生成
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
下表给出了卡方独立性检验中5个常用的小概率值和临界值。
典例分析
例4:某儿童医院用甲、乙两种疗法治疗小儿消化不良,采用有放回简单随机抽样的方法对治疗情况进行检查,得到如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名;试根据小概率值 的独立性检验,分析乙种疗法的效果是否比甲种疗法好。
疗法 疗效
合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
典例分析
例4:为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法,调查了9965认,得到成对样本观测数据的分类统计结果,如下表。依据小概率值 的独立性检验,分析吸烟是否会增加患肺癌的风险。
吸烟 肺癌
合计
非肺癌患者 肺癌患者 非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
规律总结
课堂小结
1. 正相关、负相关、线性相关;
2.样本相关系数的公式;
3.一元线性回归模型、经验回归方程,以及一元线性回归模型中参数的最小二乘估计;
3.决定系数的公式;
4.列联表和独立性检验,能通过列联表和独立性检验解决基本的实际问题。
作业布置
教材课本P135习题8.3第5-7题.
THANKS
第八章 成对数据的统计分析
学习目标
1. 理解正相关、负相关、线性相关的概念;掌握样本相关系数的公式,能利用样本相关系数描述成对样本数据的数字特征。
2.通过具体案例理解一元线性回归模型、经验回归方程,以及一元线性回归模型中参数的最小二乘估计。
3.掌握决定系数的公式,并能利用决定系数判断不同模型拟合的效果。
4.掌握列联表和独立性检验的概念,并能通过列联表和独立性检验解决基本的实际问题。
8.1 成对数据的统计相关性
引言
频率分布直方图描述样本数据的分布规律,均值刻画样本数据的击中趋势,用方差刻画样本数据的离散程度,这些方法适用于通过样本认识单个变量的统计规律。
在现实中,我们经常需要了解两个或两个以上变量之间的关系,例如教育部门为掌握学生身体健康状况,需要了解身高变量和体重变量之间的关系;医疗部门要制定预防青少年近视的措施,需要了解有哪儿些因素会影响视力,以及这些因素是如何影响视力的;商家要根据顾客的意见改进服务水平,希望了解哪儿些因素影响服务水平,以及这些因素是如何起作用的。为此我们需要进一步通过样本推断变量之间关系的知识和方法。
8.1.1 变量的相关关系
一个人的体重与他的身高有关系,一般来说,个子高的人往往体重值较大,个子矮的人往往体重值较小,但是身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素。像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系。
用散点图展示成对样本数据的变化特征,图中散点大致落在一条直线附近,就可以推断两个变量之间存在着相关关系。
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,称这两个变量正相关;当一个变量的值增加时,另一个变量的值呈现减小的趋势,称这两个变量负相关.如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,称这两个变量线性相关。如果两个变量具有相关性,但不是线性相关,称这两个变量非线性相关或曲线相关.
8.1.2 样本相关系数
散点图虽然能直观地看出两个变量是否存在相关关系,但无法确切地反映成对样本数据的相关程度,我们需要引入样本相关系数r来量化两个变量之间的相关程度的大小。
典例解析
例1:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机抽样数据,如下表。表中每个编号下面的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据。
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?如果线性相关请计算样本相关系数,并推断它们的相关程度。
(1)这些散点大致落在一条从左下角到右上角的直线附近,表明随着年龄值的增加,相应的脂肪含量值呈现增加的趋势(正相关),因此脂肪含量和年龄变量之间线性相关。
典例分析
8.2 一元线性回归模型及其应用
8.2.1 一元线性回归模型
通过前面的学习,我们已经学会推断两个变量是否存在相关关系以及相关程度的大小。如果能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系,那么我们可以利用这两个模型研究两个变量之间的随机关系,并通过模型进行预测.
例2:生活经验告诉我们,儿子的身高与父亲的身高不仅线性相关,而且正相关,即父亲的身高较高时,儿子的身高通常也比较高。为了进一步研究两者之间的关系,有人调查了某所高校14名男大学生的身高及其父亲的身高,得到的数据如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
根据题意可得,儿子身高和父亲身高线性相关,且r≈0.886,相关程度较高
思考:儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
由此可见,儿子身高和父亲身高之间不是函数关系,也就不能用函数模型刻画。
散点大致分布在一条直线附近,表明儿子身高和父亲身高这两个变量之间有较强的线性相关关系,因此可以用一次函数来刻画父亲身高对儿子身高的影响,而把影响儿子身高的其他因素,如目前身高、生活环境、饮食习惯等作为误差,得到刻画两个变量之间关系的线性回归模型,其中随机误差是一个随机变量.
概念生成
8.2.2 一元线性回归模型参数的最小二乘估计
8.2.2 一元线性回归模型参数的最小二乘估计
残差比较均匀地分布在横轴(x=0)的两侧,
说明该模型满足一元线性回归模型的假设。
典例分析
例3:人们将男子短跑100m的高水平运动员称为“百米飞人”。下表给出1968年之前男子短跑100m世界纪录产生的年份
和世界记录的数据。试根据这些成对数据,建立男子短跑100m世界纪录关于记录产生年份的经验回归方程。
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
以成对数据中的世界纪录产生年份为生坐标,世界纪录为纵坐标作散点图,得到右图.
散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程。
典例分析
8.3 列联表与独立性检验
8.3.1 分类变量与列联表
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题,例如:就读不同学校是否对学生的成绩有影响;不同班级学生用于体育锻炼的时间是否有差别;吸烟是否会增加患肺癌的风险等等.
在讨论上述问题时,为了方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量。分类变量的取值可以用实数表示,例如:学生所在的班级可以用1,2,3表示;男性,女性可以用1,0表示等等。在很多时候,这些数值只作为编号使用,并没有通常的大小和现实意义。本节我们主要讨论取值{0,1}的分类变量的关联性问题。
例4:为了有针对性提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查,数据如下:523名女生中有331名经常锻炼;601名男生中有473名经常锻炼。你能利用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗?
为了清晰,我们用表格整理数据,如下:
性别 锻炼
合计
不经常(Y=0) 经常(Y=1) 女生(X=0) 192 331 523
男生(X=1) 128 473 601
合计 320 804 1124
2×2列联表
8.3.2 独立性检验
前面我们通过列联表整理成对分类变量的样本观测数据,并根据随机事件频率的稳定性推断两个分类变量之间是否有关联。对于随机样本而言,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误概率可能性会较大。因此需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算.
X Y
合计
Y=0 Y=1 X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
概念生成
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
下表给出了卡方独立性检验中5个常用的小概率值和临界值。
典例分析
例4:某儿童医院用甲、乙两种疗法治疗小儿消化不良,采用有放回简单随机抽样的方法对治疗情况进行检查,得到如下数据:抽到接受甲种疗法的患儿67名,其中未治愈15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名;试根据小概率值 的独立性检验,分析乙种疗法的效果是否比甲种疗法好。
疗法 疗效
合计
未治愈 治愈 甲 15 52 67
乙 6 63 69
合计 21 115 136
典例分析
例4:为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法,调查了9965认,得到成对样本观测数据的分类统计结果,如下表。依据小概率值 的独立性检验,分析吸烟是否会增加患肺癌的风险。
吸烟 肺癌
合计
非肺癌患者 肺癌患者 非吸烟者 7775 42 7817
吸烟者 2099 49 2148
合计 9874 91 9965
规律总结
课堂小结
1. 正相关、负相关、线性相关;
2.样本相关系数的公式;
3.一元线性回归模型、经验回归方程,以及一元线性回归模型中参数的最小二乘估计;
3.决定系数的公式;
4.列联表和独立性检验,能通过列联表和独立性检验解决基本的实际问题。
作业布置
教材课本P135习题8.3第5-7题.
THANKS
