3.2.1复数代数形式的加减运算及其几何意义
文档属性
| 名称 | 3.2.1复数代数形式的加减运算及其几何意义 |  | |
| 格式 | rar | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-05 15:43:00 | ||
图片预览




文档简介
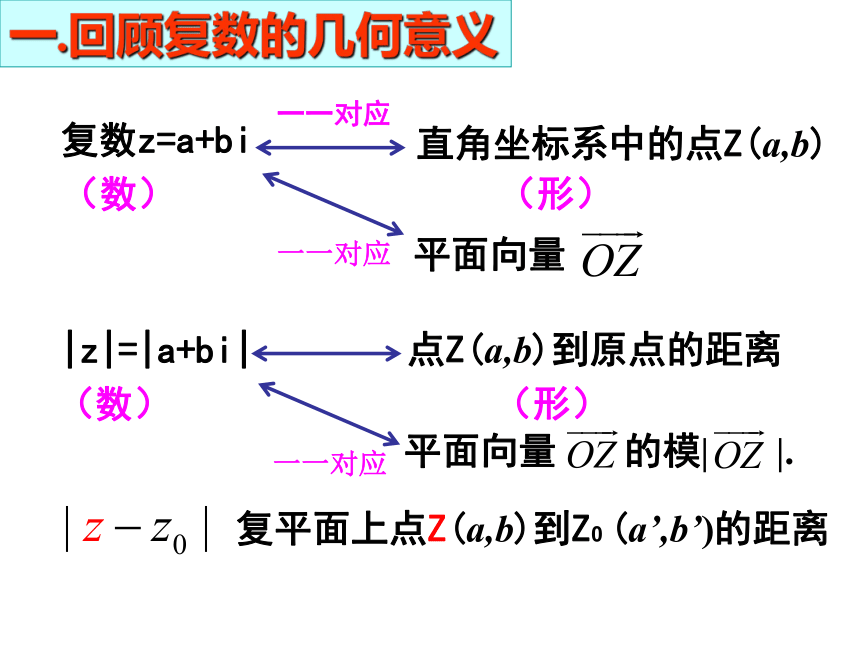
课件11张PPT。复数的加减运算及其几何意义复数z=a+bi(数)(形)一.回顾复数的几何意义|z|=|a+bi|(数)(形)复平面上点Z(a,b)到Z0 (a’,b’)的距离二.复数的加减法及几何意义设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R)1、加法:则Z1+Z2=(a+bi)+(c+di)=(a+c)+(b+d)i设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R)2、减法:则Z1-Z2=(a+bi)-(c+di)=(a-c)+(b-d)i例1.计算(1)(1+3i)+(-4+2i)
(2)(5-6i)+(-2-i)-(3+4i)
(3) 已知(3-ai)-(b+4i)=2a-bi,求实数a、b的值。二.复数的加减法及几何意义3、共轭复数:实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。二.复数的加减法及几何意义xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形 法则.1.复数加法运算的几何意义?新课讲解xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离例1.设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
(1)|z- 2|= 1;(2)|z-1+i|=2(3)|z-1+i|<=2复数减法的几何意义的运用例2.设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
1.| z- i| + | z + i|= 4
2.| z- 2| = | z + 4|1.|z1|= |z2|
平行四边形OABC是2.| z1+ z2|= | z1- z2|
平行四边形OABC是3. |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形三、复数加减法的几何意义三、复数加减法的几何意义的运用练习1:设z1,z2∈C,|z1|=|z2|=1,|z2+z1|=
求|z2-z1|.练习2:复数z1,z2分别对应复平面内的点M1,M2,且| z2+ z1|=| z2- z1|,线段M1M2的中点M对应的复数为4+3i,求|z1|2 + |z2|2
(2)(5-6i)+(-2-i)-(3+4i)
(3) 已知(3-ai)-(b+4i)=2a-bi,求实数a、b的值。二.复数的加减法及几何意义3、共轭复数:实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。二.复数的加减法及几何意义xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1 +OZ2 = OZ符合向量加法的平行四边形 法则.1.复数加法运算的几何意义?新课讲解xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离例1.设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
(1)|z- 2|= 1;(2)|z-1+i|=2(3)|z-1+i|<=2复数减法的几何意义的运用例2.设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
1.| z- i| + | z + i|= 4
2.| z- 2| = | z + 4|1.|z1|= |z2|
平行四边形OABC是2.| z1+ z2|= | z1- z2|
平行四边形OABC是3. |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是oz2-z1ABC菱形矩形正方形三、复数加减法的几何意义三、复数加减法的几何意义的运用练习1:设z1,z2∈C,|z1|=|z2|=1,|z2+z1|=
求|z2-z1|.练习2:复数z1,z2分别对应复平面内的点M1,M2,且| z2+ z1|=| z2- z1|,线段M1M2的中点M对应的复数为4+3i,求|z1|2 + |z2|2
