第5单元 生活中的多边形-多边形的面积 单元高频易错培优卷(含解析)-2025-2026学年五年级上册数学青岛版(六三学制)
文档属性
| 名称 | 第5单元 生活中的多边形-多边形的面积 单元高频易错培优卷(含解析)-2025-2026学年五年级上册数学青岛版(六三学制) |

|
|
| 格式 | docx | ||
| 文件大小 | 472.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 08:44:31 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年五年级上册数学单元高频易错培优卷青岛版(六三学制)
第5单元 生活中的多边形-多边形的面积
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题
1.有长度是3厘米、4厘米、5厘米和9厘米的小棒各一根,从中选出三根可以围成一个三角形,这个三角形恰好是一个直角三角形,它的面积是( )cm2。
A.6 B.7.5 C.10 D.12
2.下列图中,每个大正方形都是由四个边长为1的小正方形组成,其中阴影面积不等于2的图形是( )。
A. B. C. D.
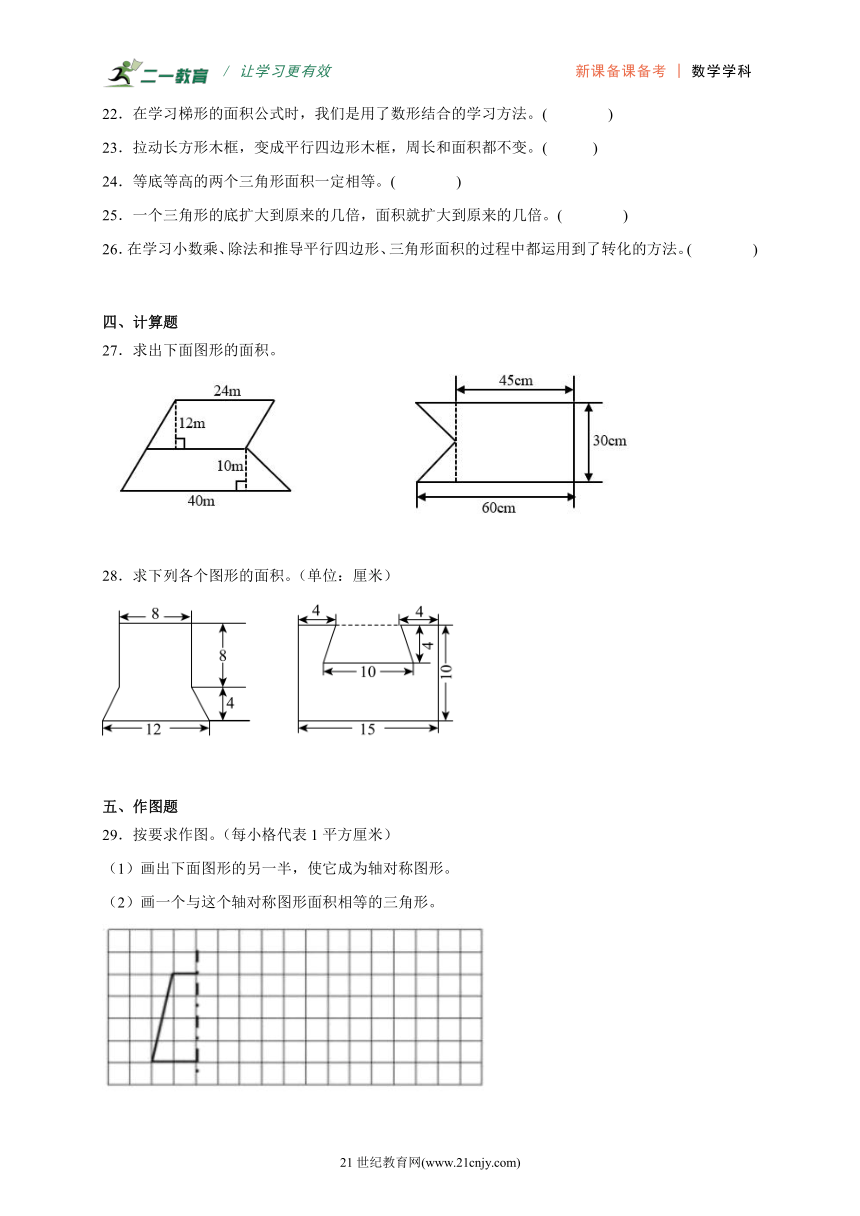
3.图中阴影部分与空白部分相比( )。
A.面积相等,周长相等 B.面积不等,周长相等
C.面积相等,周长不等 D.面积不等,周长不等
4.把一根铁丝围成的长方形拉成平行四边形,它的( )不变,( )改变。
A.周长;面积 B.面积;周长 C.周长;周长
5.如图,一组平行线中有三个图形,比较这三个图形的面积( )。
A.三角形的面积最大
B.平行四边形的面积最大
C.梯形的面积最大
D.三个图形的面积一样大
6.一个梯形的上底延长为原来的4倍,下底也延长为原来的4倍,高不变,面积( )。
A.不变 B.扩大为原来的4倍
C.扩大为原来的8倍 D.扩大为原来的16倍
7.下图是由五个相同的正方形拼成的,图中两个阴影部分的面积相比( )。
A.①的面积大 B.②的面积大 C.相等
8.下面的两个长方形完全相同,阴影部分的面积相比,( )。
A. B. C. D.无法确定
9.一个平行四边形的底不变,要使面积扩大到原来的4倍,高应( )。
A.扩大到原来的2倍 B.扩大到原来的4倍 C.扩大到原来的8倍
10.两个完全一样的梯形拼成一个面积是52.4平方厘米的平行四边形,则每个梯形的面积是( )平方厘米。
A.26.2 B.52.4 C.10.8
二、填空题
11.已知一个五边形的三条边的长和四个角,如图所示,那么,这个五边形的面积是 。
12.一个面积是22平方米的三角形的花园,园丁叔叔把这个花园的底扩建成原来的1.5倍,高没变,现在花园的面积是( )平方米。
13.如图,齐鲁同学把一张长为10厘米的长方形纸片按图中提示进行翻折,折出的两个直角三角形面积相等且一条直角边的长度都为3厘米,折出的平行四边形面积比原来的长方形面积少了15平方厘米,那么折出的平行四边形面积为 平方厘米。
14.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是0.6分米,那么三角形的高是( )分米。
15.一个直角三角形的三条边分别是6厘米,8厘米和10厘米,这个三角形的面积是( ),斜边上的高是( )。
16.如图,一个面积为8cm2的梯形,剪拼成平行四边形后,平行四边形的高是( )cm。
17.将一个可活动的平行四边形框架拉成一个长方形,长方形的面积( )原来平行四边形的面积,长方形的周长( )原来平行四边形的周长。(填“>”“<”或“=”)
18.一个三角形的底是6cm,高是2.5cm,这个三角形的面积是( )cm2,与它等底等高的平行四边形的面积是( )cm2。
19.如图,将一个上底是5厘米,下底是8厘米的梯形剪拼成一个平行四边形,剪拼成的平行四边形的底是( )厘米,高是( )厘米。此时平行四边形的面积是( )平方厘米。原来梯形的面积是( )平方厘米。
20.观察下面一组图,图3长方形的面积是平方厘米,宽是厘米,图1梯形上、下底的和是( )厘米。
三、判断题
21.如果1平方米可以站8个小朋友,那么2公顷可以站16000个小朋友。( )
22.在学习梯形的面积公式时,我们是用了数形结合的学习方法。( )
23.拉动长方形木框,变成平行四边形木框,周长和面积都不变。( )
24.等底等高的两个三角形面积一定相等。( )
25.一个三角形的底扩大到原来的几倍,面积就扩大到原来的几倍。( )
26.在学习小数乘、除法和推导平行四边形、三角形面积的过程中都运用到了转化的方法。( )
四、计算题
27.求出下面图形的面积。
28.求下列各个图形的面积。(单位:厘米)
五、作图题
29.按要求作图。(每小格代表1平方厘米)
(1)画出下面图形的另一半,使它成为轴对称图形。
(2)画一个与这个轴对称图形面积相等的三角形。
30.操作。
(1)画出图①的另一半,使它成为一个轴对称图形。
(2)在方格纸上(每小格均为边长1厘米的正方形),以AB为一条边画一个面积是4cm2的三角形;再将画出的三角形绕B点顺时针方向旋转90度,画出旋转后的图形。
六、解答题
31.农业观光园是具备一定辅助设施和集科技示范、生态观光、产业开发于一体的综合园区。一个长方形的农业观光园,占地面积是2平方千米,长是2000米。这个长方形的农业观光园的周长是多少米?
32.《周礼》中记载:“诸公之地,封疆方五百里,其食者半。”在古代,“方”指面积,“方五百里”就是指正方形边长是五百里。如果1里=500米,那么文中“诸公之地”有多少平方米?合多少公顷?
33.古代步兵作战进攻时常用“锥形阵”,其前部是一个等腰三角形,紧跟着的是一个长方形,如图是在一次小型战役中使用的一个锥形阵。
(1)你能求出它的面积吗?
(2)要击退锥形阵,还必须有足够的弓箭,如果每100平方米需要280支箭,在这次作战中至少要准备多少支箭?
34.一块平行四边形草坪,中间有一条石子路,如果铺1平方米的草坪需要8.5元,那么铺这块草坪需要多少钱?
35.根据相关研究,室外景点低于0.75平方米/人时,就会有发生踩踏事故的危险。在一个古镇景点的戏台前有一片底是50米,高是66米的平行四边形室外场地。为保证安全,这片场地最多能容纳多少人同时看戏?
36.王大伯计划用篱笆一边靠墙围成如图的一块梯形菜地,菜地的面积是76平方米,王大伯把菜地分成了两个三角形,大三角形种西红柿,每株西红柿占地0.25平方米,小三角形种辣椒,每平方米6株。
(1)王大伯要围这块梯形菜地至少需要多长的篱笆?
(2)请在上图中标出西红柿的种植区域。算一算,王大伯要分别买多少株西红柿苗和辣椒苗?
37.据资料显示,室外场所,若人均占有面积低于0.75平方米时,就会有发生踩踏事故的危险,宋城大舞台的观众席是一个近似梯形的场地,上底50米,下底80米,高为37.5米。请你帮工作人员算算。安全起见,每一场最多能允许多少人同时观看演出?
38.学校有一块梯形的空地作为劳动实验基地(如图),A地种白菜,B地种萝卜,C地种辣椒,高是8米。
(1)每平方米收白菜27千克,A地能收白菜多少千克?
(2)每0.25平方米栽一棵萝卜,B地可以栽多少棵萝卜?
39.疫情防控期间,各学校都采取扫健康码、测量体温、错峰入校等措施保障学生安全。学生入校后需按照指定路线直接到达教室。下图是某学校路上的一个导向箭头,这个导向箭头的面积是多少平方厘米?
40.植物是制造氧气的“工厂”,根据测算,1平方米的草坪每天能够释放0.9千克的氧气。(如下图)学校建了一个梯形草坪,中间有一条宽2米的石子路。这块草坪每天能释放氧气多少千克?
/ 让学习更有效 新课备课备考 | 数学学科
/ 让学习更有效 新课备课备考 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】根据三角形任意两边之和大于第三条边,3+4<9,4+5=9,3+4>5,两个直角边分别是3厘米和4厘米;结合直角三角形面积公式:两个直角边相乘除以2。
【解析】3厘米+4厘米>5厘米
3×4÷2=6(平方厘米)
则它的面积是6平方厘米
故答案为:A
2.D
【分析】A.阴影部分是一个底为1,高为2的平行四边形;
B.阴影面积=大正方形的面积-2个空白三角形的面积;
C.阴影面积=上面阴影三角形的面积+下面阴影三角形的面积;
D.阴影面积=左边阴影梯形面积+右边阴影三角形面积之和;
根据平行四边形的面积=底×高,正方形的面积=边长×边长,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,求出各图形中阴影的面积,据此找出阴影面积不等于2的图形。
【解析】A.4×2=2
阴影面积等于2,不符合题意;
B.2×2-2×1÷2×2
=4-2
=2
阴影面积等于2,不符合题意;
C.2×1÷2+2×1÷2
=1+1
=2
阴影面积等于2,不符合题意;
D.(1+2)×1÷2+1×2÷2
=3×1÷2+1×2÷2
=1.5+1
=2.5
阴影部分面积不等于2,符合题意。
故答案为:D
3.C
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,看图可知,阴影部分是2个三角形,2个三角形的底相加是平行四边形的底,2个三角形与平行四边形等高,因此阴影部分的面积是平行四边形面积的一半,所以空白部分的面积也是平行四边形面积的一半;
封闭图形一周的长度是周长,阴影部分的周长=平行四边形的底+公共边的长度,空白部分的周长=平行四边形的底+2条平行四边形的斜边+公共边的长度,周长不相等。
【解析】根据三角形的面积公式可知:阴影部分的面积、空白部分的面积均是平行四边形面积的一半,而阴影部分的周长=平行四边形的底+公共边的长度,空白部分的周长=平行四边形的底+2条平行四边形的斜边+公共边的长度,所以周长不相等。
故答案为:C
4.A
【分析】平面图形的周长就是围成它的所有线段的长度和;将长方形拉成平行四边形后,每个边的长度没变,所以它的周长就不变,但平行四边形的高变得比原长方形的宽小,面积变小,据此解答。
【解析】根据分析可知,把一根铁丝围成的长方形拉成平行四边形,它的周长不变,面积改变。
故答案为:A
5.A
【分析】观察图形可知,这三个图形在同一组平行线之中,根据“两条平行线之间所有的垂线段相等”可知,这三个图形的高相等,可以设它们的高都是h;
然后根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,分别求出这三个图形的面积,再比较,得出哪个图形的面积最大。
【解析】设平行四边形、三角形、梯形的高都是h;
平行四边形的面积:8×h=8h
三角形的面积:18×h÷2=9h
梯形的面积:
(5+11)×h÷2
=16×h÷2
=8h
9h>8h
比较这三个图形的面积,三角形的面积最大。
故答案为:A
6.B
【分析】设出原来梯形的上底、下底和高的数值,根据题意,得出延长后梯形的上底、下底和高的数值,再根据梯形的面积=(上底+下底)×高÷2,分别求出变化前后梯形的面积,用延长后梯形的面积除以原来梯形的面积,得出结论。
【解析】假设原来梯形的上底为2,下底为3,高为2;
原来梯形的面积:
(2+3)×2÷2
=5×2÷2
=5
延长后梯形的上底为2×4=8,下底为3×4=12,高为2;
延长后梯形的面积:
(8+12)×2÷2
=20×2÷2
=20
面积扩大为原来的:
20÷5=4
所以,面积扩大为原来的4倍。
故答案为:B
7.C
【分析】观察题意可知,①三角形的底和高都等于正方形的边长,②三角形的底和高也都等于正方形的边长,根据三角形的面积=底×高÷2,可知如果两个三角形的底相等、高也相等,则两个三角形的面积也相等。
【解析】根据分析可知,两个阴影部分的三角形是等底等高的,所以它们的面积是相等的。
故答案为:C
8.B
【分析】观察图形可知,三角形M的底相当于长方形的长,高相当于长方形的宽;三角形N的底相当于长方形的宽,高相当于长方形的长,根据长方形的面积=长×高,三角形的面积=底×高÷2,又因为两个长方形完全相同,所以三角形M和三角形N的面积相等。
【解析】由分析可知:
两个长方形完全相同,阴影部分的面积相等,即。
故答案为:B
9.B
【分析】平行四边形的面积=底×高,再根据积的变化规律,如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么积也扩大(或缩小)相同倍数,据此解答。
【解析】平行四边形面积=底×高,根据积的变化规律,平行四边形的底不变,要使面积扩大到原来的4倍,那么高也应扩大到原来的4倍。
故答案为:B
【点评】解答本题的关键是根据平行四边形的面积计算公式,结合积的变化规律来解答。
10.A
【分析】两个完全一样的梯形可以拼成一个平行四边形。这个平行四边形的面积是原来两个梯形面积的和,即为每个梯形面积的2倍,可用平行四边形的面积除以2进行计算即可得到每个梯形的面积,据此解答即可。
【解析】52.4÷2=26.2(平方厘米)
所以每个梯形的面积是26.2平方厘米。
故答案为:A
【点评】两个完全一样的平面图形拼成一个图形,其面积就等于原图形的面积的2倍。
11.18
【分析】
如图所示,过C点作CD垂直于AE交于点D,则∠DCF=45°,∠E=45°,∠EGF=45°,即△CDE和△GFE都是等腰三角形,则CD=DE=5,GF=FE=3;这个五边形的面积=△CDE的面积+长方形ABCD的面积-△GFE的面积;根据三角形的面积=底×高÷2,长方形的面积=长×宽,代入相应数值计算,即可解答。
【解析】5×5÷2+5×2-3×3÷2
=25÷2+10-9÷2
=12.5+10-4.5
=22.5-4.5
=18
因此这个五边形的面积是18。
【点评】解答此题的关键是将组合图形分为三角形和长方形,然后再减去多的三角形部分,再通过角的关系,明确三角形的形状,即可求出图形的面积。
12.33
【分析】三角形的面积=底×高÷2。由题意得,园丁叔叔把花园的底扩建成原来的1.5倍,高没变,那么这个花园的面积就变为原来的1.5倍。三角形花园原来的面积为22平方米,那么直接用22乘1.5即可算出现在花园的面积。
【解析】22×1.5=33(平方米)
故现在花园的面积是33平方米。
13.35
【分析】已知折出的平行四边形面积比原来的长方形面积少了15平方厘米,即两个直角三角形的面积是15平方厘米,除以2即是一个直角三角形的面积;
已知一条直角边的长度为3厘米,根据三角形的面积=底×高÷2,可知三角形的高=面积×2÷底,求出直角三角形的另一条直角边,也就是长方形的宽;
已知长方形的长为10厘米,根据长方形的面积=长×宽,求出长方形的面积,再减去15平方厘米,即是平行四边形的面积。
【解析】一个直角三角形的面积:15÷2=7.5(平方厘米)
直角三角形的另一条直角边(长方形的宽):
7.5×2÷3
=15÷3
=5(厘米)
长方形的面积:10×5=50(平方厘米)
平行四边形的面积:50-15=35(平方厘米)
所以,折出的平行四边形的面积是35平方厘米。
14.1.2
【分析】根据三角形和平行四边形面积的关系:等底等高的平行四边形面积是三角形面积的2倍。题干中三角形和平行四边形底边相等,要使面积相等,则三角形的高是平行四边形高的2倍。据此可得出答案。
【解析】三角形与一个平行四边形的底相等,面积也相等,则三角形的高是平行四边形高的2倍。平行四边形的高是0.6分米,那么三角形高是:0.6×2=1.2(分米)。
15.24平方厘米 4.8厘米
【分析】直角三角形的斜边最长,所以这个直角三角形的斜边是10厘米,另两条边都是直角边,直角三角形的两条直角边互为底和高,根据三角形的面积=底×高÷2,用6×8÷2列式求出直角三角形的面积,再用三角形的面积乘2,再除以斜边即可求出斜边上的高。
【解析】6×8÷2
=48÷2
=24(平方厘米)
24×2÷10
=48÷10
=4.8(厘米)
所以这个三角形的面积是24平方厘米,斜边上的高是4.8厘米。
16.2
【分析】根据图示可知,平行四边形的面积等于梯形的面积,平行四边形的底是梯形上底与下底的和,再根据平行四边形的面积=底×高,用梯形的面积除以梯形上底与下底的和,即可求得平行四边形的高。
【解析】8÷(1.2+2.8)
=8÷4
=2(cm)
所以平行四边形的高是2cm。
17.> =
【分析】将一个可活动的平行四边形框架拉成一个长方形,因为围成图形的线段的长度不变,则长方形的周长等于平行四边形的周长;长方形的长等于平行四边形的底,长方形的宽大于平行四边形的高,根据长方形的面积=长×宽,平行四边形的面积=底×高,可得:长方形的面积大于原来平行四边形的面积。
【解析】通过分析可得:将一个可活动的平行四边形框架拉成一个长方形,长方形的面积>原来平行四边形的面积,长方形的周长=原来平行四边形的周长。
18.7.5 15
【分析】已知三角形的底和高,根据三角形的面积=底×高÷2,求出这个三角形的面积;
根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知当平行四边形和三角形等底等高时,平行四边形的面积是三角形面积的2倍,据此解答。
【解析】6×2.5÷2
=15÷2
=7.5(cm2)
7.5×2=15(cm2)
这个三角形的面积是7.5cm2,与它等底等高的平行四边形的面积是15cm2。
19.13 5 65 65
【分析】将梯形剪拼成图中的平行四边形,平行四边形面积=梯形面积,平行四边形的底=梯形的上底+下底,平行四边形的高=梯形的高÷2,根据平行四边形面积=底×高,求出平行四边形面积,也是梯形面积。
【解析】5+8=13(厘米)
10÷2=5(厘米)
13×5=65(平方厘米)
剪拼成的平行四边形的底是13厘米,高是5厘米。此时平行四边形的面积是65平方厘米。原来梯形的面积是65平方厘米。
20.
【分析】观察图形可知:经过剪拼图1梯形和图3长方形的面积相等,图1梯形的高和图3长方形的宽是相等的。图3长方形的面积是S平方厘米,即图1梯形的面积是S平方厘米;图3长方形的宽是b厘米,即图1梯形的高是b厘米。根据“梯形的面积=(上底+下底)×高÷2”可推导出,梯形的上底+下底=梯形的面积×2÷高。据此可表示出图1梯形上、下底的和。
【解析】=(厘米)
所以,图1梯形上、下底的和是厘米。
21.×
【分析】由题意知,根据1公顷=10000平方米,先将2公顷转换为平方米,再计算总人数。
【解析】2×10000=20000(平方米)
每平方米可站8个小朋友,总人数为:
20000×8=160000(个)
故答案为:×
22.√
【分析】在学习梯形的面积公式时,我们将两个完全一样的梯形拼成了一个平行四边形(如下图),然后利用平行四边形的面积公式推导出了梯形的面积公式,整个过程运用了数形结合的学习方法。
【解析】由分析得,学习梯形的面积公式时,我们用了数形结合的学习方法。原题说法正确。
故答案为:√
23.×
【分析】封闭图形一周的长度是这个图形的周长,因此平行四边形的周长=邻边长度之和×2,平行四边形的面积=底×高,长方形的面积=长×宽。拉动长方形木框,变成平行四边形木框,则木框的总长度不变,但是长方形的宽大于平行四边形的高,依此判断。
【解析】根据分析可知,拉动长方形木框,变成平行四边形木框,周长不变,面积改变了。
故答案为:×
24.√
【分析】三角形面积=底×高÷2,三角形的面积与底和高有关,等底等高的两个三角形,面积相等,据此分析。
【解析】等底等高的两个三角形面积一定相等,说法正确。
故答案为:√
25.×
【分析】根据三角形的面积=底×高÷2,以及积的变化规律“一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”,据此判断。
【解析】根据三角形的面积公式以及积的变化规律可知,一个三角形的高不变,对应的底扩大到原来的几倍,面积就扩大到原来的几倍。
原题说法错误。
故答案为:×
26.√
【分析】计算小数乘除法是转化成整数乘除法,也就是按照整数乘除法的计算方法来计算的,举例计算0.2×0.3、0.8÷0.2;平行四边形面积公式的推导是将平行四边形面积转化成长方形面积,三角形面积公式的推导是将三角形转化成平行四边形进行计算;据此解答。
【解析】在推导小数乘除计算方法和组合图形面积的计算时,都用到了转化的数学方法。如:计算0.2×0.3时,转化成2×3=6,再从右边数出两位点上小数点得0.06;计算0.8÷0.2时,转化成8÷2=4;平行四边形面积公式的推导是将平行四边形面积转化成长方形面积,三角形面积公式的推导是将三角形转化成平行四边形进行计算。
所以,在学习小数乘、除法和推导平行四边形、三角形面积的过程中都运用到了转化的方法。原说法正确。
故答案为:√
27.608平方米;1575平方厘米
【分析】左图是由一个底为24米,高为12米的平行四边形和一个上底为24米,下底为40米,高为10米的梯形组合而成,分别利用平行四边形和梯形的面积公式求出这两个图形的面积,再相加即可求出组合图形的面积;
右图是由一个长为60厘米,宽为30厘米的长方形减去一个底为30厘米,高为(60-45)厘米的三角形,分别利用长方形和三角形的面积公式求出这两个图形的面积,再相减即可求出组合图形的面积。
【解析】24×12+(24+40)×10÷2
=288+64×10÷2
=288+320
=608(平方米)
60×30-30×(60-45)÷2
=1800-30×15÷2
=1800-225
=1575(平方厘米)
即左图的面积是608平方米,右图的面积是1575平方厘米。
28.(1)104平方厘米
(2)116平方厘米
【分析】(1)组合图形的面积=正方形的面积+梯形的面积,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,计算即可;
(2)组合图形的面积=长方形的面积-梯形的面积,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,计算即可。
【解析】根据分析得:
(1)8×8+(8+12)×4÷2
=64+(8+12)×4÷2
=64+20×4÷2
=64+80÷2
=64+40
=104(平方厘米)
(2)15×10-(15-4×2+10)×4÷2
=150-(15-4×2+10)×4÷2
=150-(15-8+10)×4÷2
=150-(7+10)×4÷2
=150-17×4÷2
=150-68÷2
=150-34
=116(平方厘米)
29.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到图形的另一半,使它成为轴对称图形。
(2)轴对称图形是一个梯形,根据梯形的面积=(上底+下底)×高÷2,求出它的面积;
要画一个与这个梯形面积相等的三角形,根据三角形的面积=底×高÷2,确定三角形的底和高,据此画出这个三角形。
【解析】(1)画出图形的另一半,使它成为轴对称图形,见下图。
(2)梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
三角形的面积:6×4÷2=12(平方厘米)
画一个底为6厘米、高为4厘米的三角形,如下图。
(三角形画法不唯一)
30.(1)(2)见详解
【分析】(1)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴是对称点的连线的垂线,在对称轴的另一边画出图形的几个顶点,再依次连线即可;
(2)根据三角形面积=底×高÷2,已知一条边AB为4cm,将数据代入可以求出该三角形的高,据此画图即可(三角形不唯一);根据旋转的特征,三角形绕B点顺时针方向旋转90度,点B位置不动,这个三角形的各部分均绕此点按相同方向旋转相同度数即可画出旋转后的图形。
【解析】由分析可得:
4×2÷4
=8÷4
=2(cm)
该三角形以AB为一条边,高为2cm,据此画图,
(1)(2)画图如下:
(三角形画法不唯一)
【点评】此题考查的知识点有:作轴对称图形,作指定面积的三角形、作旋转一定度数后的图形,以上知识都需要熟练掌握并且灵活运用,尤其需要能结合知识准确画图。
31.6000米
【分析】根据1千米=1000米,将2000米单位化为千米是2千米,所以可根据长方形面积公式:长宽,求出宽1千米,根据长方形周长公式:(长宽),求出长方形的周长。
【解析】长:2000米=2千米
宽:2÷2=1(千米)
周长:(2+1)×2=6(千米)
6千米=6000米
答:这个长方形的农业观光园的周长是6000米。
32.62500000000平方米,合6250000公顷
【分析】由题意知,正方形边长500里,根据1里=500米将500里转化成米,求出正方形面积=边长×边长。根据10000平方米=1公顷换算单位即可。
【解析】500×500=250000(米)
250000×250000=62500000000(平方米)
62500000000平方米=6250000公顷
答:“诸公之地”有62500000000平方米,合6250000公顷。
33.(1)87000平方米
(2)243600支
【分析】(1)观察图形可知,锥形阵的面积=长方形的面积+三角形的面积,根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数据计算求解。
(2)已知每100平方米需要280支箭,先用除法求出锥形阵的面积里有多少个100平方米,再乘280,即可求出在这次战斗中至少要准备箭的支数。
【解析】(1)240×300+(450-300)×200÷2
=72000+150×200÷2
=72000+30000÷2
=72000+15000
=87000(平方米)
答:锥形阵的面积是87000平方米。
(2)87000÷100×280
=870×280
=243600(支)
答:在这次作战中至少要准备243600支箭。
34.1224元
【分析】根据平行四边形的面积=底×高,分别算整块地的面积和石子路的面积,然后用整块地的面积减去石子路的面积,即可求出所需铺草坪的面积;然后用草坪的面积乘铺每平方米草坪所需的费用,即可求出总的费用。
【解析】(20×8-2×8)×8.5
=(160-16)×8.5
=144×8.5
=1224(元)
答:铺这块草坪需要1224元钱。
35.4400人
【分析】室外景点低于0.75平方米/人时,就会有发生踩踏事故的危险。当室外景点是0.75平方米/人时,此时既保证了安全又能使容纳的人数最多。根据公式:平行四边形的面积=底×高,即可求出这个场地的面积,再用这个场地的面积除以0.75,就是最多能容纳的人数。
【解析】50×66=3300(平方米)
3300÷0.75=4400(人)
答:为保证安全,这片场地最多能容纳4400人同时看戏。
36.(1)27米
(2)作图见详解;西红柿苗192株,辣椒苗168株
【分析】(1)观察可知,篱笆长包括上下底的和以及高,根据梯形上下底的和=面积×2÷高,求出上下底的和,再加上高,就是篱笆长;
(2)将梯形分成两个三角形,分别以梯形的上底和下底作为三角形的底,画一条对角线,分成两个三角形即可。梯形的上底=上下底的和-下底,根据三角形面积=底×高÷2,分别求出西红柿和辣椒的面积,西红柿苗的面积÷每株西红柿的占地面积=西红柿苗的数量,辣椒的面积×每平方米数量=辣椒苗的数量,据此列式解答。
【解析】(1)76×2÷8+8
=19+8
=27(米)
答:至少需要27米的篱笆。
(2)或
西红柿:12×8÷2÷0.25
=48÷0.25
=192(株)
辣椒:76×2÷8-12
=19-12
=7(米)
7×8÷2×6
=28×6
=168(株)
答:西红柿苗要买192株,辣椒苗要买168株。
37.3250人
【分析】根据梯形的面积=(上底+下底)×高÷2,据此求出舞台的面积,再用舞台的面积除以0.75即可求出最多能允许多少人同时观看演出。
【解析】(50+80)×37.5÷2
=130×37.5÷2
=4875÷2
=2437.5(平方米)
2437.5÷0.75=3250(人)
答:安全起见,每一场最多能允许3250人同时观看演出。
38.(1)1296千克
(2)192棵
【分析】(1)A地是个梯形,高与C地的高相同,根据梯形的面积=(上底+下底)×高÷2,代入数据,先求出A地的面积,再用A地的面积乘每平方米收白菜的千克数即可解答。
(2)先根据平行四边形的面积=底×高,计算出平行四边形的面积,用平行四边形的面积除以栽一棵萝卜的面积,即可计算出可以栽萝卜的数量。
【解析】(1)(3+9)×8÷2
=12×8÷2
=96÷2
=48(平方米)
27×48=1296(千克)
答:A地能收白菜1296千克。
(2)6×8÷0.25
=48÷0.25
=192(棵)
答:B地可以栽192棵萝卜。
39.4200平方厘米
【分析】根据题意可知,这个导向箭头的面积相当于一个长80厘米、宽35厘米的长方形面积加上底是70厘米、高是40厘米的三角形面积;根据长方形的面积=长×宽、三角形的面积=底×高÷2,代入数据求出两个图形的面积,再相加即可。
【解析】
(平方厘米)
答:这个导向箭头的面积是4200平方厘米。
40.170.1千克
【分析】先根据梯形的面积求出上底是10米,下底是15米,高是18米的梯形的面积;再根据平行四边形的面积求出底是2米,高是18米的平行四边形的面积;再用梯形面积减去平行四边形的面积求出草坪的面积;最后用草坪的面积乘每天每平方米草坪释放氧气的千克数,求出这块草坪每天释放氧气的千克数。
【解析】梯形的面积:(10+15)×18÷2
=25×18÷2
=450÷2
=225(平方米)
平行四边形的面积:2×18=36(平方米)
(225-36)×0.9
=189×0.9
=170.1(千克)
答:这块草坪每天能释放氧气170.1千克。
【点评】此题考查了梯形和平行四边形的面积计算公式。计算梯形面积时,不要忘记除以2。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年五年级上册数学单元高频易错培优卷青岛版(六三学制)
第5单元 生活中的多边形-多边形的面积
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题
1.有长度是3厘米、4厘米、5厘米和9厘米的小棒各一根,从中选出三根可以围成一个三角形,这个三角形恰好是一个直角三角形,它的面积是( )cm2。
A.6 B.7.5 C.10 D.12
2.下列图中,每个大正方形都是由四个边长为1的小正方形组成,其中阴影面积不等于2的图形是( )。
A. B. C. D.
3.图中阴影部分与空白部分相比( )。
A.面积相等,周长相等 B.面积不等,周长相等
C.面积相等,周长不等 D.面积不等,周长不等
4.把一根铁丝围成的长方形拉成平行四边形,它的( )不变,( )改变。
A.周长;面积 B.面积;周长 C.周长;周长
5.如图,一组平行线中有三个图形,比较这三个图形的面积( )。
A.三角形的面积最大
B.平行四边形的面积最大
C.梯形的面积最大
D.三个图形的面积一样大
6.一个梯形的上底延长为原来的4倍,下底也延长为原来的4倍,高不变,面积( )。
A.不变 B.扩大为原来的4倍
C.扩大为原来的8倍 D.扩大为原来的16倍
7.下图是由五个相同的正方形拼成的,图中两个阴影部分的面积相比( )。
A.①的面积大 B.②的面积大 C.相等
8.下面的两个长方形完全相同,阴影部分的面积相比,( )。
A. B. C. D.无法确定
9.一个平行四边形的底不变,要使面积扩大到原来的4倍,高应( )。
A.扩大到原来的2倍 B.扩大到原来的4倍 C.扩大到原来的8倍
10.两个完全一样的梯形拼成一个面积是52.4平方厘米的平行四边形,则每个梯形的面积是( )平方厘米。
A.26.2 B.52.4 C.10.8
二、填空题
11.已知一个五边形的三条边的长和四个角,如图所示,那么,这个五边形的面积是 。
12.一个面积是22平方米的三角形的花园,园丁叔叔把这个花园的底扩建成原来的1.5倍,高没变,现在花园的面积是( )平方米。
13.如图,齐鲁同学把一张长为10厘米的长方形纸片按图中提示进行翻折,折出的两个直角三角形面积相等且一条直角边的长度都为3厘米,折出的平行四边形面积比原来的长方形面积少了15平方厘米,那么折出的平行四边形面积为 平方厘米。
14.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是0.6分米,那么三角形的高是( )分米。
15.一个直角三角形的三条边分别是6厘米,8厘米和10厘米,这个三角形的面积是( ),斜边上的高是( )。
16.如图,一个面积为8cm2的梯形,剪拼成平行四边形后,平行四边形的高是( )cm。
17.将一个可活动的平行四边形框架拉成一个长方形,长方形的面积( )原来平行四边形的面积,长方形的周长( )原来平行四边形的周长。(填“>”“<”或“=”)
18.一个三角形的底是6cm,高是2.5cm,这个三角形的面积是( )cm2,与它等底等高的平行四边形的面积是( )cm2。
19.如图,将一个上底是5厘米,下底是8厘米的梯形剪拼成一个平行四边形,剪拼成的平行四边形的底是( )厘米,高是( )厘米。此时平行四边形的面积是( )平方厘米。原来梯形的面积是( )平方厘米。
20.观察下面一组图,图3长方形的面积是平方厘米,宽是厘米,图1梯形上、下底的和是( )厘米。
三、判断题
21.如果1平方米可以站8个小朋友,那么2公顷可以站16000个小朋友。( )
22.在学习梯形的面积公式时,我们是用了数形结合的学习方法。( )
23.拉动长方形木框,变成平行四边形木框,周长和面积都不变。( )
24.等底等高的两个三角形面积一定相等。( )
25.一个三角形的底扩大到原来的几倍,面积就扩大到原来的几倍。( )
26.在学习小数乘、除法和推导平行四边形、三角形面积的过程中都运用到了转化的方法。( )
四、计算题
27.求出下面图形的面积。
28.求下列各个图形的面积。(单位:厘米)
五、作图题
29.按要求作图。(每小格代表1平方厘米)
(1)画出下面图形的另一半,使它成为轴对称图形。
(2)画一个与这个轴对称图形面积相等的三角形。
30.操作。
(1)画出图①的另一半,使它成为一个轴对称图形。
(2)在方格纸上(每小格均为边长1厘米的正方形),以AB为一条边画一个面积是4cm2的三角形;再将画出的三角形绕B点顺时针方向旋转90度,画出旋转后的图形。
六、解答题
31.农业观光园是具备一定辅助设施和集科技示范、生态观光、产业开发于一体的综合园区。一个长方形的农业观光园,占地面积是2平方千米,长是2000米。这个长方形的农业观光园的周长是多少米?
32.《周礼》中记载:“诸公之地,封疆方五百里,其食者半。”在古代,“方”指面积,“方五百里”就是指正方形边长是五百里。如果1里=500米,那么文中“诸公之地”有多少平方米?合多少公顷?
33.古代步兵作战进攻时常用“锥形阵”,其前部是一个等腰三角形,紧跟着的是一个长方形,如图是在一次小型战役中使用的一个锥形阵。
(1)你能求出它的面积吗?
(2)要击退锥形阵,还必须有足够的弓箭,如果每100平方米需要280支箭,在这次作战中至少要准备多少支箭?
34.一块平行四边形草坪,中间有一条石子路,如果铺1平方米的草坪需要8.5元,那么铺这块草坪需要多少钱?
35.根据相关研究,室外景点低于0.75平方米/人时,就会有发生踩踏事故的危险。在一个古镇景点的戏台前有一片底是50米,高是66米的平行四边形室外场地。为保证安全,这片场地最多能容纳多少人同时看戏?
36.王大伯计划用篱笆一边靠墙围成如图的一块梯形菜地,菜地的面积是76平方米,王大伯把菜地分成了两个三角形,大三角形种西红柿,每株西红柿占地0.25平方米,小三角形种辣椒,每平方米6株。
(1)王大伯要围这块梯形菜地至少需要多长的篱笆?
(2)请在上图中标出西红柿的种植区域。算一算,王大伯要分别买多少株西红柿苗和辣椒苗?
37.据资料显示,室外场所,若人均占有面积低于0.75平方米时,就会有发生踩踏事故的危险,宋城大舞台的观众席是一个近似梯形的场地,上底50米,下底80米,高为37.5米。请你帮工作人员算算。安全起见,每一场最多能允许多少人同时观看演出?
38.学校有一块梯形的空地作为劳动实验基地(如图),A地种白菜,B地种萝卜,C地种辣椒,高是8米。
(1)每平方米收白菜27千克,A地能收白菜多少千克?
(2)每0.25平方米栽一棵萝卜,B地可以栽多少棵萝卜?
39.疫情防控期间,各学校都采取扫健康码、测量体温、错峰入校等措施保障学生安全。学生入校后需按照指定路线直接到达教室。下图是某学校路上的一个导向箭头,这个导向箭头的面积是多少平方厘米?
40.植物是制造氧气的“工厂”,根据测算,1平方米的草坪每天能够释放0.9千克的氧气。(如下图)学校建了一个梯形草坪,中间有一条宽2米的石子路。这块草坪每天能释放氧气多少千克?
/ 让学习更有效 新课备课备考 | 数学学科
/ 让学习更有效 新课备课备考 | 数学学科
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】根据三角形任意两边之和大于第三条边,3+4<9,4+5=9,3+4>5,两个直角边分别是3厘米和4厘米;结合直角三角形面积公式:两个直角边相乘除以2。
【解析】3厘米+4厘米>5厘米
3×4÷2=6(平方厘米)
则它的面积是6平方厘米
故答案为:A
2.D
【分析】A.阴影部分是一个底为1,高为2的平行四边形;
B.阴影面积=大正方形的面积-2个空白三角形的面积;
C.阴影面积=上面阴影三角形的面积+下面阴影三角形的面积;
D.阴影面积=左边阴影梯形面积+右边阴影三角形面积之和;
根据平行四边形的面积=底×高,正方形的面积=边长×边长,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,求出各图形中阴影的面积,据此找出阴影面积不等于2的图形。
【解析】A.4×2=2
阴影面积等于2,不符合题意;
B.2×2-2×1÷2×2
=4-2
=2
阴影面积等于2,不符合题意;
C.2×1÷2+2×1÷2
=1+1
=2
阴影面积等于2,不符合题意;
D.(1+2)×1÷2+1×2÷2
=3×1÷2+1×2÷2
=1.5+1
=2.5
阴影部分面积不等于2,符合题意。
故答案为:D
3.C
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,看图可知,阴影部分是2个三角形,2个三角形的底相加是平行四边形的底,2个三角形与平行四边形等高,因此阴影部分的面积是平行四边形面积的一半,所以空白部分的面积也是平行四边形面积的一半;
封闭图形一周的长度是周长,阴影部分的周长=平行四边形的底+公共边的长度,空白部分的周长=平行四边形的底+2条平行四边形的斜边+公共边的长度,周长不相等。
【解析】根据三角形的面积公式可知:阴影部分的面积、空白部分的面积均是平行四边形面积的一半,而阴影部分的周长=平行四边形的底+公共边的长度,空白部分的周长=平行四边形的底+2条平行四边形的斜边+公共边的长度,所以周长不相等。
故答案为:C
4.A
【分析】平面图形的周长就是围成它的所有线段的长度和;将长方形拉成平行四边形后,每个边的长度没变,所以它的周长就不变,但平行四边形的高变得比原长方形的宽小,面积变小,据此解答。
【解析】根据分析可知,把一根铁丝围成的长方形拉成平行四边形,它的周长不变,面积改变。
故答案为:A
5.A
【分析】观察图形可知,这三个图形在同一组平行线之中,根据“两条平行线之间所有的垂线段相等”可知,这三个图形的高相等,可以设它们的高都是h;
然后根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,分别求出这三个图形的面积,再比较,得出哪个图形的面积最大。
【解析】设平行四边形、三角形、梯形的高都是h;
平行四边形的面积:8×h=8h
三角形的面积:18×h÷2=9h
梯形的面积:
(5+11)×h÷2
=16×h÷2
=8h
9h>8h
比较这三个图形的面积,三角形的面积最大。
故答案为:A
6.B
【分析】设出原来梯形的上底、下底和高的数值,根据题意,得出延长后梯形的上底、下底和高的数值,再根据梯形的面积=(上底+下底)×高÷2,分别求出变化前后梯形的面积,用延长后梯形的面积除以原来梯形的面积,得出结论。
【解析】假设原来梯形的上底为2,下底为3,高为2;
原来梯形的面积:
(2+3)×2÷2
=5×2÷2
=5
延长后梯形的上底为2×4=8,下底为3×4=12,高为2;
延长后梯形的面积:
(8+12)×2÷2
=20×2÷2
=20
面积扩大为原来的:
20÷5=4
所以,面积扩大为原来的4倍。
故答案为:B
7.C
【分析】观察题意可知,①三角形的底和高都等于正方形的边长,②三角形的底和高也都等于正方形的边长,根据三角形的面积=底×高÷2,可知如果两个三角形的底相等、高也相等,则两个三角形的面积也相等。
【解析】根据分析可知,两个阴影部分的三角形是等底等高的,所以它们的面积是相等的。
故答案为:C
8.B
【分析】观察图形可知,三角形M的底相当于长方形的长,高相当于长方形的宽;三角形N的底相当于长方形的宽,高相当于长方形的长,根据长方形的面积=长×高,三角形的面积=底×高÷2,又因为两个长方形完全相同,所以三角形M和三角形N的面积相等。
【解析】由分析可知:
两个长方形完全相同,阴影部分的面积相等,即。
故答案为:B
9.B
【分析】平行四边形的面积=底×高,再根据积的变化规律,如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么积也扩大(或缩小)相同倍数,据此解答。
【解析】平行四边形面积=底×高,根据积的变化规律,平行四边形的底不变,要使面积扩大到原来的4倍,那么高也应扩大到原来的4倍。
故答案为:B
【点评】解答本题的关键是根据平行四边形的面积计算公式,结合积的变化规律来解答。
10.A
【分析】两个完全一样的梯形可以拼成一个平行四边形。这个平行四边形的面积是原来两个梯形面积的和,即为每个梯形面积的2倍,可用平行四边形的面积除以2进行计算即可得到每个梯形的面积,据此解答即可。
【解析】52.4÷2=26.2(平方厘米)
所以每个梯形的面积是26.2平方厘米。
故答案为:A
【点评】两个完全一样的平面图形拼成一个图形,其面积就等于原图形的面积的2倍。
11.18
【分析】
如图所示,过C点作CD垂直于AE交于点D,则∠DCF=45°,∠E=45°,∠EGF=45°,即△CDE和△GFE都是等腰三角形,则CD=DE=5,GF=FE=3;这个五边形的面积=△CDE的面积+长方形ABCD的面积-△GFE的面积;根据三角形的面积=底×高÷2,长方形的面积=长×宽,代入相应数值计算,即可解答。
【解析】5×5÷2+5×2-3×3÷2
=25÷2+10-9÷2
=12.5+10-4.5
=22.5-4.5
=18
因此这个五边形的面积是18。
【点评】解答此题的关键是将组合图形分为三角形和长方形,然后再减去多的三角形部分,再通过角的关系,明确三角形的形状,即可求出图形的面积。
12.33
【分析】三角形的面积=底×高÷2。由题意得,园丁叔叔把花园的底扩建成原来的1.5倍,高没变,那么这个花园的面积就变为原来的1.5倍。三角形花园原来的面积为22平方米,那么直接用22乘1.5即可算出现在花园的面积。
【解析】22×1.5=33(平方米)
故现在花园的面积是33平方米。
13.35
【分析】已知折出的平行四边形面积比原来的长方形面积少了15平方厘米,即两个直角三角形的面积是15平方厘米,除以2即是一个直角三角形的面积;
已知一条直角边的长度为3厘米,根据三角形的面积=底×高÷2,可知三角形的高=面积×2÷底,求出直角三角形的另一条直角边,也就是长方形的宽;
已知长方形的长为10厘米,根据长方形的面积=长×宽,求出长方形的面积,再减去15平方厘米,即是平行四边形的面积。
【解析】一个直角三角形的面积:15÷2=7.5(平方厘米)
直角三角形的另一条直角边(长方形的宽):
7.5×2÷3
=15÷3
=5(厘米)
长方形的面积:10×5=50(平方厘米)
平行四边形的面积:50-15=35(平方厘米)
所以,折出的平行四边形的面积是35平方厘米。
14.1.2
【分析】根据三角形和平行四边形面积的关系:等底等高的平行四边形面积是三角形面积的2倍。题干中三角形和平行四边形底边相等,要使面积相等,则三角形的高是平行四边形高的2倍。据此可得出答案。
【解析】三角形与一个平行四边形的底相等,面积也相等,则三角形的高是平行四边形高的2倍。平行四边形的高是0.6分米,那么三角形高是:0.6×2=1.2(分米)。
15.24平方厘米 4.8厘米
【分析】直角三角形的斜边最长,所以这个直角三角形的斜边是10厘米,另两条边都是直角边,直角三角形的两条直角边互为底和高,根据三角形的面积=底×高÷2,用6×8÷2列式求出直角三角形的面积,再用三角形的面积乘2,再除以斜边即可求出斜边上的高。
【解析】6×8÷2
=48÷2
=24(平方厘米)
24×2÷10
=48÷10
=4.8(厘米)
所以这个三角形的面积是24平方厘米,斜边上的高是4.8厘米。
16.2
【分析】根据图示可知,平行四边形的面积等于梯形的面积,平行四边形的底是梯形上底与下底的和,再根据平行四边形的面积=底×高,用梯形的面积除以梯形上底与下底的和,即可求得平行四边形的高。
【解析】8÷(1.2+2.8)
=8÷4
=2(cm)
所以平行四边形的高是2cm。
17.> =
【分析】将一个可活动的平行四边形框架拉成一个长方形,因为围成图形的线段的长度不变,则长方形的周长等于平行四边形的周长;长方形的长等于平行四边形的底,长方形的宽大于平行四边形的高,根据长方形的面积=长×宽,平行四边形的面积=底×高,可得:长方形的面积大于原来平行四边形的面积。
【解析】通过分析可得:将一个可活动的平行四边形框架拉成一个长方形,长方形的面积>原来平行四边形的面积,长方形的周长=原来平行四边形的周长。
18.7.5 15
【分析】已知三角形的底和高,根据三角形的面积=底×高÷2,求出这个三角形的面积;
根据平行四边形的面积=底×高,三角形的面积=底×高÷2,可知当平行四边形和三角形等底等高时,平行四边形的面积是三角形面积的2倍,据此解答。
【解析】6×2.5÷2
=15÷2
=7.5(cm2)
7.5×2=15(cm2)
这个三角形的面积是7.5cm2,与它等底等高的平行四边形的面积是15cm2。
19.13 5 65 65
【分析】将梯形剪拼成图中的平行四边形,平行四边形面积=梯形面积,平行四边形的底=梯形的上底+下底,平行四边形的高=梯形的高÷2,根据平行四边形面积=底×高,求出平行四边形面积,也是梯形面积。
【解析】5+8=13(厘米)
10÷2=5(厘米)
13×5=65(平方厘米)
剪拼成的平行四边形的底是13厘米,高是5厘米。此时平行四边形的面积是65平方厘米。原来梯形的面积是65平方厘米。
20.
【分析】观察图形可知:经过剪拼图1梯形和图3长方形的面积相等,图1梯形的高和图3长方形的宽是相等的。图3长方形的面积是S平方厘米,即图1梯形的面积是S平方厘米;图3长方形的宽是b厘米,即图1梯形的高是b厘米。根据“梯形的面积=(上底+下底)×高÷2”可推导出,梯形的上底+下底=梯形的面积×2÷高。据此可表示出图1梯形上、下底的和。
【解析】=(厘米)
所以,图1梯形上、下底的和是厘米。
21.×
【分析】由题意知,根据1公顷=10000平方米,先将2公顷转换为平方米,再计算总人数。
【解析】2×10000=20000(平方米)
每平方米可站8个小朋友,总人数为:
20000×8=160000(个)
故答案为:×
22.√
【分析】在学习梯形的面积公式时,我们将两个完全一样的梯形拼成了一个平行四边形(如下图),然后利用平行四边形的面积公式推导出了梯形的面积公式,整个过程运用了数形结合的学习方法。
【解析】由分析得,学习梯形的面积公式时,我们用了数形结合的学习方法。原题说法正确。
故答案为:√
23.×
【分析】封闭图形一周的长度是这个图形的周长,因此平行四边形的周长=邻边长度之和×2,平行四边形的面积=底×高,长方形的面积=长×宽。拉动长方形木框,变成平行四边形木框,则木框的总长度不变,但是长方形的宽大于平行四边形的高,依此判断。
【解析】根据分析可知,拉动长方形木框,变成平行四边形木框,周长不变,面积改变了。
故答案为:×
24.√
【分析】三角形面积=底×高÷2,三角形的面积与底和高有关,等底等高的两个三角形,面积相等,据此分析。
【解析】等底等高的两个三角形面积一定相等,说法正确。
故答案为:√
25.×
【分析】根据三角形的面积=底×高÷2,以及积的变化规律“一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几”,据此判断。
【解析】根据三角形的面积公式以及积的变化规律可知,一个三角形的高不变,对应的底扩大到原来的几倍,面积就扩大到原来的几倍。
原题说法错误。
故答案为:×
26.√
【分析】计算小数乘除法是转化成整数乘除法,也就是按照整数乘除法的计算方法来计算的,举例计算0.2×0.3、0.8÷0.2;平行四边形面积公式的推导是将平行四边形面积转化成长方形面积,三角形面积公式的推导是将三角形转化成平行四边形进行计算;据此解答。
【解析】在推导小数乘除计算方法和组合图形面积的计算时,都用到了转化的数学方法。如:计算0.2×0.3时,转化成2×3=6,再从右边数出两位点上小数点得0.06;计算0.8÷0.2时,转化成8÷2=4;平行四边形面积公式的推导是将平行四边形面积转化成长方形面积,三角形面积公式的推导是将三角形转化成平行四边形进行计算。
所以,在学习小数乘、除法和推导平行四边形、三角形面积的过程中都运用到了转化的方法。原说法正确。
故答案为:√
27.608平方米;1575平方厘米
【分析】左图是由一个底为24米,高为12米的平行四边形和一个上底为24米,下底为40米,高为10米的梯形组合而成,分别利用平行四边形和梯形的面积公式求出这两个图形的面积,再相加即可求出组合图形的面积;
右图是由一个长为60厘米,宽为30厘米的长方形减去一个底为30厘米,高为(60-45)厘米的三角形,分别利用长方形和三角形的面积公式求出这两个图形的面积,再相减即可求出组合图形的面积。
【解析】24×12+(24+40)×10÷2
=288+64×10÷2
=288+320
=608(平方米)
60×30-30×(60-45)÷2
=1800-30×15÷2
=1800-225
=1575(平方厘米)
即左图的面积是608平方米,右图的面积是1575平方厘米。
28.(1)104平方厘米
(2)116平方厘米
【分析】(1)组合图形的面积=正方形的面积+梯形的面积,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,计算即可;
(2)组合图形的面积=长方形的面积-梯形的面积,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,计算即可。
【解析】根据分析得:
(1)8×8+(8+12)×4÷2
=64+(8+12)×4÷2
=64+20×4÷2
=64+80÷2
=64+40
=104(平方厘米)
(2)15×10-(15-4×2+10)×4÷2
=150-(15-4×2+10)×4÷2
=150-(15-8+10)×4÷2
=150-(7+10)×4÷2
=150-17×4÷2
=150-68÷2
=150-34
=116(平方厘米)
29.见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点得到图形的另一半,使它成为轴对称图形。
(2)轴对称图形是一个梯形,根据梯形的面积=(上底+下底)×高÷2,求出它的面积;
要画一个与这个梯形面积相等的三角形,根据三角形的面积=底×高÷2,确定三角形的底和高,据此画出这个三角形。
【解析】(1)画出图形的另一半,使它成为轴对称图形,见下图。
(2)梯形的面积:
(2+4)×4÷2
=6×4÷2
=12(平方厘米)
三角形的面积:6×4÷2=12(平方厘米)
画一个底为6厘米、高为4厘米的三角形,如下图。
(三角形画法不唯一)
30.(1)(2)见详解
【分析】(1)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴是对称点的连线的垂线,在对称轴的另一边画出图形的几个顶点,再依次连线即可;
(2)根据三角形面积=底×高÷2,已知一条边AB为4cm,将数据代入可以求出该三角形的高,据此画图即可(三角形不唯一);根据旋转的特征,三角形绕B点顺时针方向旋转90度,点B位置不动,这个三角形的各部分均绕此点按相同方向旋转相同度数即可画出旋转后的图形。
【解析】由分析可得:
4×2÷4
=8÷4
=2(cm)
该三角形以AB为一条边,高为2cm,据此画图,
(1)(2)画图如下:
(三角形画法不唯一)
【点评】此题考查的知识点有:作轴对称图形,作指定面积的三角形、作旋转一定度数后的图形,以上知识都需要熟练掌握并且灵活运用,尤其需要能结合知识准确画图。
31.6000米
【分析】根据1千米=1000米,将2000米单位化为千米是2千米,所以可根据长方形面积公式:长宽,求出宽1千米,根据长方形周长公式:(长宽),求出长方形的周长。
【解析】长:2000米=2千米
宽:2÷2=1(千米)
周长:(2+1)×2=6(千米)
6千米=6000米
答:这个长方形的农业观光园的周长是6000米。
32.62500000000平方米,合6250000公顷
【分析】由题意知,正方形边长500里,根据1里=500米将500里转化成米,求出正方形面积=边长×边长。根据10000平方米=1公顷换算单位即可。
【解析】500×500=250000(米)
250000×250000=62500000000(平方米)
62500000000平方米=6250000公顷
答:“诸公之地”有62500000000平方米,合6250000公顷。
33.(1)87000平方米
(2)243600支
【分析】(1)观察图形可知,锥形阵的面积=长方形的面积+三角形的面积,根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数据计算求解。
(2)已知每100平方米需要280支箭,先用除法求出锥形阵的面积里有多少个100平方米,再乘280,即可求出在这次战斗中至少要准备箭的支数。
【解析】(1)240×300+(450-300)×200÷2
=72000+150×200÷2
=72000+30000÷2
=72000+15000
=87000(平方米)
答:锥形阵的面积是87000平方米。
(2)87000÷100×280
=870×280
=243600(支)
答:在这次作战中至少要准备243600支箭。
34.1224元
【分析】根据平行四边形的面积=底×高,分别算整块地的面积和石子路的面积,然后用整块地的面积减去石子路的面积,即可求出所需铺草坪的面积;然后用草坪的面积乘铺每平方米草坪所需的费用,即可求出总的费用。
【解析】(20×8-2×8)×8.5
=(160-16)×8.5
=144×8.5
=1224(元)
答:铺这块草坪需要1224元钱。
35.4400人
【分析】室外景点低于0.75平方米/人时,就会有发生踩踏事故的危险。当室外景点是0.75平方米/人时,此时既保证了安全又能使容纳的人数最多。根据公式:平行四边形的面积=底×高,即可求出这个场地的面积,再用这个场地的面积除以0.75,就是最多能容纳的人数。
【解析】50×66=3300(平方米)
3300÷0.75=4400(人)
答:为保证安全,这片场地最多能容纳4400人同时看戏。
36.(1)27米
(2)作图见详解;西红柿苗192株,辣椒苗168株
【分析】(1)观察可知,篱笆长包括上下底的和以及高,根据梯形上下底的和=面积×2÷高,求出上下底的和,再加上高,就是篱笆长;
(2)将梯形分成两个三角形,分别以梯形的上底和下底作为三角形的底,画一条对角线,分成两个三角形即可。梯形的上底=上下底的和-下底,根据三角形面积=底×高÷2,分别求出西红柿和辣椒的面积,西红柿苗的面积÷每株西红柿的占地面积=西红柿苗的数量,辣椒的面积×每平方米数量=辣椒苗的数量,据此列式解答。
【解析】(1)76×2÷8+8
=19+8
=27(米)
答:至少需要27米的篱笆。
(2)或
西红柿:12×8÷2÷0.25
=48÷0.25
=192(株)
辣椒:76×2÷8-12
=19-12
=7(米)
7×8÷2×6
=28×6
=168(株)
答:西红柿苗要买192株,辣椒苗要买168株。
37.3250人
【分析】根据梯形的面积=(上底+下底)×高÷2,据此求出舞台的面积,再用舞台的面积除以0.75即可求出最多能允许多少人同时观看演出。
【解析】(50+80)×37.5÷2
=130×37.5÷2
=4875÷2
=2437.5(平方米)
2437.5÷0.75=3250(人)
答:安全起见,每一场最多能允许3250人同时观看演出。
38.(1)1296千克
(2)192棵
【分析】(1)A地是个梯形,高与C地的高相同,根据梯形的面积=(上底+下底)×高÷2,代入数据,先求出A地的面积,再用A地的面积乘每平方米收白菜的千克数即可解答。
(2)先根据平行四边形的面积=底×高,计算出平行四边形的面积,用平行四边形的面积除以栽一棵萝卜的面积,即可计算出可以栽萝卜的数量。
【解析】(1)(3+9)×8÷2
=12×8÷2
=96÷2
=48(平方米)
27×48=1296(千克)
答:A地能收白菜1296千克。
(2)6×8÷0.25
=48÷0.25
=192(棵)
答:B地可以栽192棵萝卜。
39.4200平方厘米
【分析】根据题意可知,这个导向箭头的面积相当于一个长80厘米、宽35厘米的长方形面积加上底是70厘米、高是40厘米的三角形面积;根据长方形的面积=长×宽、三角形的面积=底×高÷2,代入数据求出两个图形的面积,再相加即可。
【解析】
(平方厘米)
答:这个导向箭头的面积是4200平方厘米。
40.170.1千克
【分析】先根据梯形的面积求出上底是10米,下底是15米,高是18米的梯形的面积;再根据平行四边形的面积求出底是2米,高是18米的平行四边形的面积;再用梯形面积减去平行四边形的面积求出草坪的面积;最后用草坪的面积乘每天每平方米草坪释放氧气的千克数,求出这块草坪每天释放氧气的千克数。
【解析】梯形的面积:(10+15)×18÷2
=25×18÷2
=450÷2
=225(平方米)
平行四边形的面积:2×18=36(平方米)
(225-36)×0.9
=189×0.9
=170.1(千克)
答:这块草坪每天能释放氧气170.1千克。
【点评】此题考查了梯形和平行四边形的面积计算公式。计算梯形面积时,不要忘记除以2。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
