湘教版高中数学选择性必修第一册第1章数列1.2.2等差数列与一次函数课件(共45张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第1章数列1.2.2等差数列与一次函数课件(共45张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:39:52 | ||
图片预览










文档简介
(共45张PPT)
湘教版2019高一数学(选修一) 第一章 数列
1.2.2 等差数列与一次函数
1.2 等差梳理
学习目标
1.理解等差数列的通项公式与一次函数的关系.
2.掌握等差数列的判定和证明方法.
情景导入
前面我们学习了等差数列的通项公式,现在我们对它进行变形:
an=a1+(n-1)d=dn+(a1-d),
你知道它与我们熟悉的哪一类函数有关吗?
1.等差数列与一次函数
新知探究
数列可以看成以正整数集N+(或它的有限子集{1,2,…,n})为定义域的函数an = f (n),因而可以利用函数知识来研究数列的性质.我们先看两个具体例子:
求下列等差数列{an }的通项公式,并画出这个数列的图象,判断数列的单调性:
(1)a1 =7,d =3; (2)a1 =7,d =-2.
不难求得,等差数列{an }的通项公式分别
(1) an=3n-2;(2)an=-2n+9.
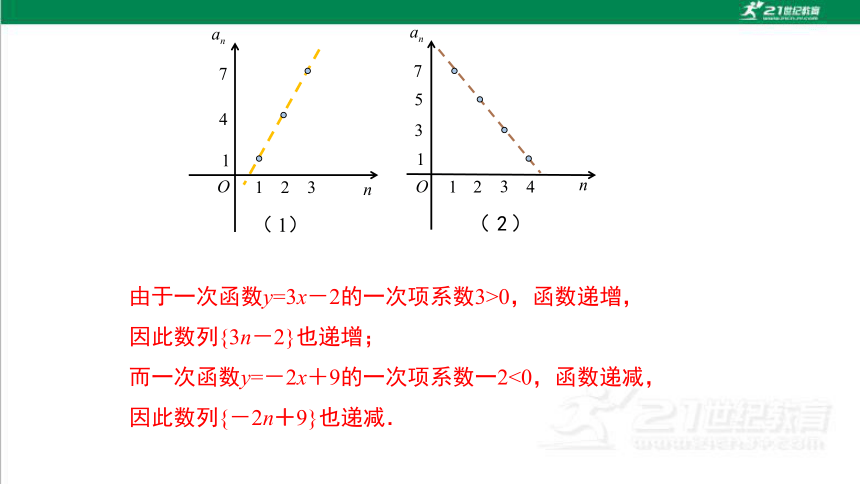
上述通项公式可以看成自变量 n 取正整数值的函数,将通项公式中的正整数自变量 n 换成实数自变量x,得到一次函数y=3x-2 和 y=-2x+9,它们的图象都是直线.
当x取正整数值 n 时,就得到an ,等差数列的图象由直线上横坐标为正整数 n 的孤立点(n,an )组成.如图 1.2-2(1)、(2)所示.
由于一次函数y=3x-2的一次项系数3>0,函数递增,
因此数列{3n-2}也递增;
而一次函数y=-2x+9的一次项系数一2<0,函数递减,
因此数列{-2n+9}也递减.
对于一般的等差数列{an },其通项公式为an=a1+(n-1)d ,将其中的
正整数自变量n换成实数自变量x,得到
y = a1+(x-1)d = dx+(a1-d).
当d≠0 时,是一次函数(其中一次项系数为等差数列的公差d );
当d=0时,y=a1(a1为常数),这两种情形的函数图象都是直线.
等差数列的图象由这条直线上横坐标为正整数 n 的孤立点(n,an )组成.
当d>0时,直线 y=d x+(a1-d )从左至右上升,等差数列{an }递增;
当d<0时,直线 y=d x+(a1-d )从左至右下降,等差数列{an }递减;
当d=0时,y=a1 为水平方向的直线,数列{an }为常数列.
概念归纳
例 4 已知数列{an}的通项公式为an=pn+q,其中p,q为常数,且p≠0,那么这个数列一定是等差数列吗?
取数列{an}中任意相邻两项an与an-1(n≥2),作差得an-an-1=pn+q-[p(n-1)+q]=p,
它是一个与n无关的常数,所以数列{an}一定是等差数列,且一次项系数p为该等差数列的公差.
课本例题
注:若 p=0,则an= q,数列{an}是常数列,也是等差数列.
例 5 已知(2,-1),(4,-7)是等差数列{an}的图象上的两点.
(1)求数列{an}的通项公式;
设等差数列{an}的首项为a1,公差为d.
因为(2,-1),(4,-7)是等差数列{an}的图象上的两点,
所以a2=-1,a4=-7,
因此,an=2+(n-1)×(-3)=-3n+5.
课本例题
(2)画出数列{an}的图象;
由(1)可知,
数列{an}的图象是均匀分布在直线
y=-3x+5上的一系列孤立点,如图.
(3)判断数列{an}的单调性.
由(1)可知公差d=-3<0,所以等差数列{an}为递减数列.
例 6 已知等差数列{an}满足ap=q,aq=p,(p,q∈N+,p ≠ q),求ap+q的值.
解: 设等差数列{an}的首项为a1,公差为d,则
a1+(p-1) d=q,a1+(q-1) d=p,
解得
a1=p+q-1,d=-1,
因此,
ap+q=a1+(p+q-1) d =(p+q-1)+(p+q-1) ×(-1) = 0.
课本例题
性质 如果数列{an}为等差数列,那么
an= am + (n-m)d,(n,m∈N+) .
证明:记等差数列{an}的公差为d,则
an=a1+(n-1)d,
am=a1+(m-1)d,
两式相减,得
an-am= (n-m)d,
即 an=am+(n-m)d .
概念归纳
例1 已知(1,3),(3,-1)是等差数列{an}图象上的两点,若5是p,q的等差中项,求ap+aq的值.
典例剖析
题型1 等差数列的通项公式的函数特征
利用等差数列通项公式与一次函数的对应关系,列方程组求解.
例 6 已知等差数列{an}满足ap=q,aq=p,(p,q∈N+,p ≠ q),求ap+q的值.
解: 设等差数列{an}的首项为a1,公差为d,则
ap=a1+(p-1) d=q, ① aq=a1+(q-1) d=p,②
①-②得 ap-aq=(p-q) d,则 ③
③式从函数的观点看,等差数列{an}的任意两项的函数值之差与相
应自变量之差的比为公差d.于是将ap,aq,与ap+q,aq分别代入③式得
解得ap+q=0.
课本例题
1.在等差数列{an}中,am=n,an=m,则am+n( )
A.0 B.m
C.n D.m+n
练一练
A
例2 已知(1,1),(3,5)是等差数列{an}图象上的两点.
(1)求这个数列的通项公式;
(2)画出这个数列的图象;
(3)判断这个数列的单调性.
题型2 等差数列的图象与一次函数的图象
典例剖析
数列是一个特殊的函数,因此也可以用图象来表示,以位置序号n为横坐标,相应的项为纵坐标,即以(n,an)为坐标描点画图,就可以得到数列的图象.因为它的定义域是正整数集N+(或它的有限子集{1,2,3,…,n}),所以其图象是一群孤立的点,这些点的个数可以是有限的,也可以是无限的.
归纳总结
D
练一练
例3 已知{an}是递增数列,且对于任意的n∈N+,an=n2+λn恒成立,求实数λ的取值范围.
典例剖析
题型3 等差数列的单调性与一次函数的单调性
归纳总结
3.在数列{an}中,an=-3n+18,则an的最大值为( )
A.15 B.0
C.6 D.不存在
解析:an=-3n+18对应的函数为y=-3x+18,易知它是R上的递减函数,
因此可知数列是递减数列,首项最大,
所以(an)max=a1=15.
练一练
A
1.对于数列{an},“an=kn+b(k,b为常数)”是“数列{an}为等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
随堂练
2.已知点(1,5),(2,3)是等差数列{an}图象上的两点,则数列{an}为( )
A.递增数列 B.递减数列
C.常数列 D.无法确定
C
B
3.在等差数列{an}中,若a2+a6=6,a5=8,则a10等于( )
A.20 B.25 C.30 D.33
随堂练
D
( )
D
错因分析
易错辨析 忽视等差数列中的隐含条件致误
D
【易错警示】
出错原因
(1)错选A,只看到了a10>1而忽视了a9≤1,是审题不仔细而致误;
(2)错选C,误认为a9<1,是由不会读题,马虎造成错误.
纠错心得
认真审题,充分挖掘题目中的隐含条件.
错因分析
1.已知数列{an}满足a1=3,且an=an+1+3(n∈N+),则下列说法正确的是( )
A.数列{an}是以3为首项,3为公差的等差数列
B.数列{an}是以3为首项,-3为公差的等差数列
C.数列{an}是以-3为首项,3为公差的等差数列
D.数列{an}是以-3为首项,-3为公差的等差数列
B
分层练习-基础
2.在递增的等差数列{an}中,a3+a6=-6,a4a5=8,公差d 等于( )
A.4 B.2
C.-2 D.2或-2
B
分层练习-基础
3.已知数列{an}是等差数列,a4=15,a7=27,则过点P(3,a3),Q(5,a5)的直线斜率为( )
4.已知等差数列{an}满足a1+a2+a3+…+a101=0,则有( )
A.a1+a101>0 B.a1+a101<0
C.a3+a99=0 D.a51=51
A
C
5.在数列{an}中,a1=5,3an+1=3an-2(n∈N+),则an等于( )
分层练习-基础
B
分层练习-基础
BD
( )
7.在数列{an}中,a1=2,a8=16,已知该数列的通项公式是关于n的一次函数,则a2 023=________.
4 046
分层练习-基础
9.在等差数列{an}中,已知am=n,an=m,求am+n的值.
从而am+n=am+(m+n-m)d=n+n·(-1)=0.
方法二 设等差数列的通项公式为an=an+b(a,b为常数),
得a=-1,b=m+n.
所以am+n=a(m+n)+b=0.
分层练习-基础
分层练习-基础
(2)求数列{an}的通项公式.
分层练习-基础
11.(多选)下列关于公差d>0的等差数列{an}的结论中,正确的是( )
A.数列{an}是递增数列
B.数列{nan}是递增数列
C.数列 是递增数列
D.数列{an+3nd}是递增数列
分层练习-巩固
AD
12.等差数列an中,若a2,a2 022为方程x2-10x+16=0的两根,则a1+a1 012+a2 023等于( )
A.10 B.15 C.20 D.40
分层练习-巩固
B
( )
B
分层练习-巩固
分层练习-巩固
15.在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,问标有*号的空格应填的数是______.
*
74
2y 186
y 103
0 x 2x
142
分层练习-拓展
记aij为第i行第j列的格中所填的数,则a52=x,a41=y.
由第3列得a33=2×103-2x,
所以2x+y=113. ①
由第1列得a21=3y,
则由第2行得a23=2×74-3y,
a33+103=a23+2x,a23=3×103-4x,
所以2×74-3y=3×103-4x,
即4x-3y=161, ②
由①②,得x=50,y=13,
故标有*号的空格应填142.
*
74
2y 186
y 103
0 x 2x
分层练习-拓展
所以满足条件的数列{an} 不唯一.
16.定义数列“从第二项起,若数列{an} 的每一项与前一项的平方差为同一常数d,则称数列{an} 为等平方差数列,d 叫作此数列的公平方差.”
已知数列{an} 为“等平方差数列”,且a1=1,a5=3.
(1)判断满足条件的数列{an} 是否唯一,并说明理由;
分层练习-拓展
(2)求正项数列{an} 的通项公式,并判断其单调性.
所以an<an+1,所以数列{an} 是递增数列.
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
1.知识清单:
(1)等差数列通项公式与一次函数的关系.
(2)证明等差数列的方法.
(3)等差数列的项与项之间的性质及应用.
2.方法归纳:定义法、公式法、构造法、解方程组法.
3.常见误区:
(1)不注意运用性质而出错或解法烦琐.
(2)实际问题中项数的确定.
对于一般的等差数列{an },其通项公式为an=a1+(n-1)d ,将其中的正整数自变量n换成实数自变量x,得到
y = a1+(x-1)d = dx+(a1-d).
等差数列的图象由这条直线上横坐标为正整数 n 的孤立点(n,an )组成.
当d>0时,直线y=d x+(a1-d )从左至右上升,等差数列{an }递增;
当d<0时,直线 y=d x+(a1-d )从左至右下降,等差数列{an }递减;
当d=0时,y=a1为水平方向的直线,数列{an }为常数列.
课堂小结
湘教版2019高一数学(选修一) 第一章 数列
1.2.2 等差数列与一次函数
1.2 等差梳理
学习目标
1.理解等差数列的通项公式与一次函数的关系.
2.掌握等差数列的判定和证明方法.
情景导入
前面我们学习了等差数列的通项公式,现在我们对它进行变形:
an=a1+(n-1)d=dn+(a1-d),
你知道它与我们熟悉的哪一类函数有关吗?
1.等差数列与一次函数
新知探究
数列可以看成以正整数集N+(或它的有限子集{1,2,…,n})为定义域的函数an = f (n),因而可以利用函数知识来研究数列的性质.我们先看两个具体例子:
求下列等差数列{an }的通项公式,并画出这个数列的图象,判断数列的单调性:
(1)a1 =7,d =3; (2)a1 =7,d =-2.
不难求得,等差数列{an }的通项公式分别
(1) an=3n-2;(2)an=-2n+9.
上述通项公式可以看成自变量 n 取正整数值的函数,将通项公式中的正整数自变量 n 换成实数自变量x,得到一次函数y=3x-2 和 y=-2x+9,它们的图象都是直线.
当x取正整数值 n 时,就得到an ,等差数列的图象由直线上横坐标为正整数 n 的孤立点(n,an )组成.如图 1.2-2(1)、(2)所示.
由于一次函数y=3x-2的一次项系数3>0,函数递增,
因此数列{3n-2}也递增;
而一次函数y=-2x+9的一次项系数一2<0,函数递减,
因此数列{-2n+9}也递减.
对于一般的等差数列{an },其通项公式为an=a1+(n-1)d ,将其中的
正整数自变量n换成实数自变量x,得到
y = a1+(x-1)d = dx+(a1-d).
当d≠0 时,是一次函数(其中一次项系数为等差数列的公差d );
当d=0时,y=a1(a1为常数),这两种情形的函数图象都是直线.
等差数列的图象由这条直线上横坐标为正整数 n 的孤立点(n,an )组成.
当d>0时,直线 y=d x+(a1-d )从左至右上升,等差数列{an }递增;
当d<0时,直线 y=d x+(a1-d )从左至右下降,等差数列{an }递减;
当d=0时,y=a1 为水平方向的直线,数列{an }为常数列.
概念归纳
例 4 已知数列{an}的通项公式为an=pn+q,其中p,q为常数,且p≠0,那么这个数列一定是等差数列吗?
取数列{an}中任意相邻两项an与an-1(n≥2),作差得an-an-1=pn+q-[p(n-1)+q]=p,
它是一个与n无关的常数,所以数列{an}一定是等差数列,且一次项系数p为该等差数列的公差.
课本例题
注:若 p=0,则an= q,数列{an}是常数列,也是等差数列.
例 5 已知(2,-1),(4,-7)是等差数列{an}的图象上的两点.
(1)求数列{an}的通项公式;
设等差数列{an}的首项为a1,公差为d.
因为(2,-1),(4,-7)是等差数列{an}的图象上的两点,
所以a2=-1,a4=-7,
因此,an=2+(n-1)×(-3)=-3n+5.
课本例题
(2)画出数列{an}的图象;
由(1)可知,
数列{an}的图象是均匀分布在直线
y=-3x+5上的一系列孤立点,如图.
(3)判断数列{an}的单调性.
由(1)可知公差d=-3<0,所以等差数列{an}为递减数列.
例 6 已知等差数列{an}满足ap=q,aq=p,(p,q∈N+,p ≠ q),求ap+q的值.
解: 设等差数列{an}的首项为a1,公差为d,则
a1+(p-1) d=q,a1+(q-1) d=p,
解得
a1=p+q-1,d=-1,
因此,
ap+q=a1+(p+q-1) d =(p+q-1)+(p+q-1) ×(-1) = 0.
课本例题
性质 如果数列{an}为等差数列,那么
an= am + (n-m)d,(n,m∈N+) .
证明:记等差数列{an}的公差为d,则
an=a1+(n-1)d,
am=a1+(m-1)d,
两式相减,得
an-am= (n-m)d,
即 an=am+(n-m)d .
概念归纳
例1 已知(1,3),(3,-1)是等差数列{an}图象上的两点,若5是p,q的等差中项,求ap+aq的值.
典例剖析
题型1 等差数列的通项公式的函数特征
利用等差数列通项公式与一次函数的对应关系,列方程组求解.
例 6 已知等差数列{an}满足ap=q,aq=p,(p,q∈N+,p ≠ q),求ap+q的值.
解: 设等差数列{an}的首项为a1,公差为d,则
ap=a1+(p-1) d=q, ① aq=a1+(q-1) d=p,②
①-②得 ap-aq=(p-q) d,则 ③
③式从函数的观点看,等差数列{an}的任意两项的函数值之差与相
应自变量之差的比为公差d.于是将ap,aq,与ap+q,aq分别代入③式得
解得ap+q=0.
课本例题
1.在等差数列{an}中,am=n,an=m,则am+n( )
A.0 B.m
C.n D.m+n
练一练
A
例2 已知(1,1),(3,5)是等差数列{an}图象上的两点.
(1)求这个数列的通项公式;
(2)画出这个数列的图象;
(3)判断这个数列的单调性.
题型2 等差数列的图象与一次函数的图象
典例剖析
数列是一个特殊的函数,因此也可以用图象来表示,以位置序号n为横坐标,相应的项为纵坐标,即以(n,an)为坐标描点画图,就可以得到数列的图象.因为它的定义域是正整数集N+(或它的有限子集{1,2,3,…,n}),所以其图象是一群孤立的点,这些点的个数可以是有限的,也可以是无限的.
归纳总结
D
练一练
例3 已知{an}是递增数列,且对于任意的n∈N+,an=n2+λn恒成立,求实数λ的取值范围.
典例剖析
题型3 等差数列的单调性与一次函数的单调性
归纳总结
3.在数列{an}中,an=-3n+18,则an的最大值为( )
A.15 B.0
C.6 D.不存在
解析:an=-3n+18对应的函数为y=-3x+18,易知它是R上的递减函数,
因此可知数列是递减数列,首项最大,
所以(an)max=a1=15.
练一练
A
1.对于数列{an},“an=kn+b(k,b为常数)”是“数列{an}为等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
随堂练
2.已知点(1,5),(2,3)是等差数列{an}图象上的两点,则数列{an}为( )
A.递增数列 B.递减数列
C.常数列 D.无法确定
C
B
3.在等差数列{an}中,若a2+a6=6,a5=8,则a10等于( )
A.20 B.25 C.30 D.33
随堂练
D
( )
D
错因分析
易错辨析 忽视等差数列中的隐含条件致误
D
【易错警示】
出错原因
(1)错选A,只看到了a10>1而忽视了a9≤1,是审题不仔细而致误;
(2)错选C,误认为a9<1,是由不会读题,马虎造成错误.
纠错心得
认真审题,充分挖掘题目中的隐含条件.
错因分析
1.已知数列{an}满足a1=3,且an=an+1+3(n∈N+),则下列说法正确的是( )
A.数列{an}是以3为首项,3为公差的等差数列
B.数列{an}是以3为首项,-3为公差的等差数列
C.数列{an}是以-3为首项,3为公差的等差数列
D.数列{an}是以-3为首项,-3为公差的等差数列
B
分层练习-基础
2.在递增的等差数列{an}中,a3+a6=-6,a4a5=8,公差d 等于( )
A.4 B.2
C.-2 D.2或-2
B
分层练习-基础
3.已知数列{an}是等差数列,a4=15,a7=27,则过点P(3,a3),Q(5,a5)的直线斜率为( )
4.已知等差数列{an}满足a1+a2+a3+…+a101=0,则有( )
A.a1+a101>0 B.a1+a101<0
C.a3+a99=0 D.a51=51
A
C
5.在数列{an}中,a1=5,3an+1=3an-2(n∈N+),则an等于( )
分层练习-基础
B
分层练习-基础
BD
( )
7.在数列{an}中,a1=2,a8=16,已知该数列的通项公式是关于n的一次函数,则a2 023=________.
4 046
分层练习-基础
9.在等差数列{an}中,已知am=n,an=m,求am+n的值.
从而am+n=am+(m+n-m)d=n+n·(-1)=0.
方法二 设等差数列的通项公式为an=an+b(a,b为常数),
得a=-1,b=m+n.
所以am+n=a(m+n)+b=0.
分层练习-基础
分层练习-基础
(2)求数列{an}的通项公式.
分层练习-基础
11.(多选)下列关于公差d>0的等差数列{an}的结论中,正确的是( )
A.数列{an}是递增数列
B.数列{nan}是递增数列
C.数列 是递增数列
D.数列{an+3nd}是递增数列
分层练习-巩固
AD
12.等差数列an中,若a2,a2 022为方程x2-10x+16=0的两根,则a1+a1 012+a2 023等于( )
A.10 B.15 C.20 D.40
分层练习-巩固
B
( )
B
分层练习-巩固
分层练习-巩固
15.在下表所示的5×5正方形的25个空格中填入正整数,使得每一行,每一列都成等差数列,问标有*号的空格应填的数是______.
*
74
2y 186
y 103
0 x 2x
142
分层练习-拓展
记aij为第i行第j列的格中所填的数,则a52=x,a41=y.
由第3列得a33=2×103-2x,
所以2x+y=113. ①
由第1列得a21=3y,
则由第2行得a23=2×74-3y,
a33+103=a23+2x,a23=3×103-4x,
所以2×74-3y=3×103-4x,
即4x-3y=161, ②
由①②,得x=50,y=13,
故标有*号的空格应填142.
*
74
2y 186
y 103
0 x 2x
分层练习-拓展
所以满足条件的数列{an} 不唯一.
16.定义数列“从第二项起,若数列{an} 的每一项与前一项的平方差为同一常数d,则称数列{an} 为等平方差数列,d 叫作此数列的公平方差.”
已知数列{an} 为“等平方差数列”,且a1=1,a5=3.
(1)判断满足条件的数列{an} 是否唯一,并说明理由;
分层练习-拓展
(2)求正项数列{an} 的通项公式,并判断其单调性.
所以an<an+1,所以数列{an} 是递增数列.
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
1.知识清单:
(1)等差数列通项公式与一次函数的关系.
(2)证明等差数列的方法.
(3)等差数列的项与项之间的性质及应用.
2.方法归纳:定义法、公式法、构造法、解方程组法.
3.常见误区:
(1)不注意运用性质而出错或解法烦琐.
(2)实际问题中项数的确定.
对于一般的等差数列{an },其通项公式为an=a1+(n-1)d ,将其中的正整数自变量n换成实数自变量x,得到
y = a1+(x-1)d = dx+(a1-d).
等差数列的图象由这条直线上横坐标为正整数 n 的孤立点(n,an )组成.
当d>0时,直线y=d x+(a1-d )从左至右上升,等差数列{an }递增;
当d<0时,直线 y=d x+(a1-d )从左至右下降,等差数列{an }递减;
当d=0时,y=a1为水平方向的直线,数列{an }为常数列.
课堂小结
同课章节目录
