湘教版高中数学选择性必修第一册第1章数列1.1数列的概念(第1课时) 课件(共57张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第1章数列1.1数列的概念(第1课时) 课件(共57张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 00:00:00 | ||
图片预览









文档简介
(共57张PPT)
湘教版2019高一数学(选修一) 第一章 数列
第一课时 数列的概念及其通项公式
1.1 数列的概念
学习目标
(1)理解数列的有关概念和几种简单的表示方法(重点)
(2) 发现数列的规律,找出数列可能的通项公式(难点)
(3)掌握数列通项公式概念及其应用(重点、难点)
情景导入
有人说,大自然是懂数学的,例如树木的分叉、花瓣的数量、植物种子的排列等等,都遵循着某种数学规律,大家能想到它们涉及了哪些数学规律吗?
通过本节课的学习,这些问题都会得到解决.
1.数列的概念
新知探究
在现实世界中,许多事物的数量可以排成一列数.例如:
(1)如下图所示,在超市的货架上摆放有一些罐头,最顶上一层有 2 听罐头,其余每一层的罐头数都比它上面一层的罐头数多 2,共堆了 8 层,则从上到下每层的罐头数依次为:
2,4,6,8,10,12,14,16. ①
(2)《庄子·天下》有一句话:"一尺之棰,日取其半,万世不竭."意思是∶一尺长的木棒,每日取其一半,永远也取不完.这样,每日剩下的部分都是前一天的一半. 如果把"一尺之棰"看成单位"1",那么每日剩下的部分依次为: ②
(4)π,2π,3π,4π,…的正弦值依次为:
0,0,0,0,… ④
(3)某家庭一年内1-12月的用电量(单位∶kW/h)依次为:
110,120,90,80,62,80,103,115,84,65,81,95. ③
(5)正整数1,2,3,4,5,6,…被 3除的余数依次为:
1,2,0,1,2,0,1,2,0,…. ⑤
概念归纳
把这些例子的共同特征抽象出来,得到数列的概念∶
按照一定顺序排成的一列数叫作数列.
数列中的每一个数叫作这个数列的项,排在第一位的数叫作数列的
首项或叫作数列的第1项,排在第二位的数叫作数列的第 2 项,……,
排在第n位的数叫作数列的第n项,所以数列的一般形式可以写成
a1,a2,…,an,… 简记为{an}.
数列分类:
项数有限的数列称为有穷数列,如数列①、③;
项数无限的数列称为无穷数列,如数列②、④、⑤.
上面的数列 ②中,每一项的序号n与对应项an,有如下关系式:
这样,根据以上公式我们可以求出数列②的任意指定的项.
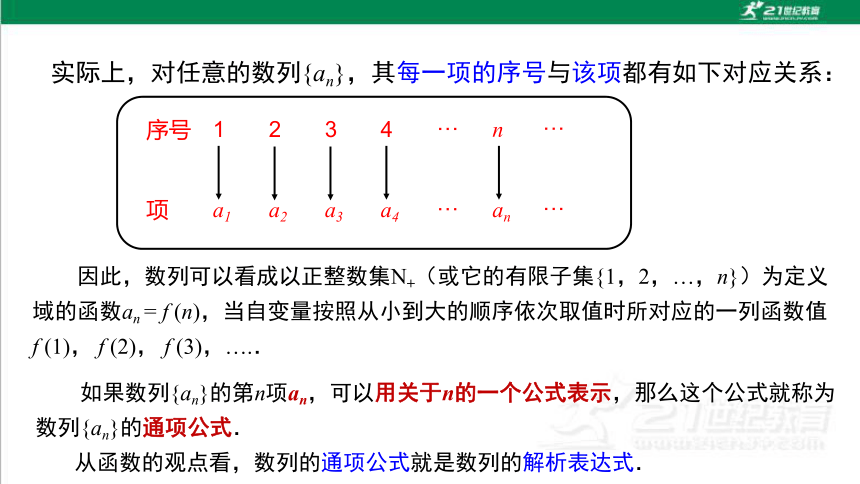
实际上,对任意的数列{an},其每一项的序号与该项都有如下对应关系:
2.数列的表示—通项公式
新知探究
序号
项
1
2
3
4
···
n
···
a1
a2
a3
a4
···
an
···
实际上,对任意的数列{an},其每一项的序号与该项都有如下对应关系:
因此,数列可以看成以正整数集N+(或它的有限子集{1,2,…,n})为定义域的函数an = f (n),当自变量按照从小到大的顺序依次取值时所对应的一列函数值 f (1), f (2), f (3),…..
如果数列{an}的第n项an,可以用关于n的一个公式表示,那么这个公式就称为数列{an}的通项公式.
从函数的观点看,数列的通项公式就是数列的解析表达式.
3.数列的表示 - 列表法
新知探究
例如,数列① 2,4,6,8,10,12,14,16.
② 的一个通项公式分别是:
与函数一样,数列还可以用列表法和图象法来表示.
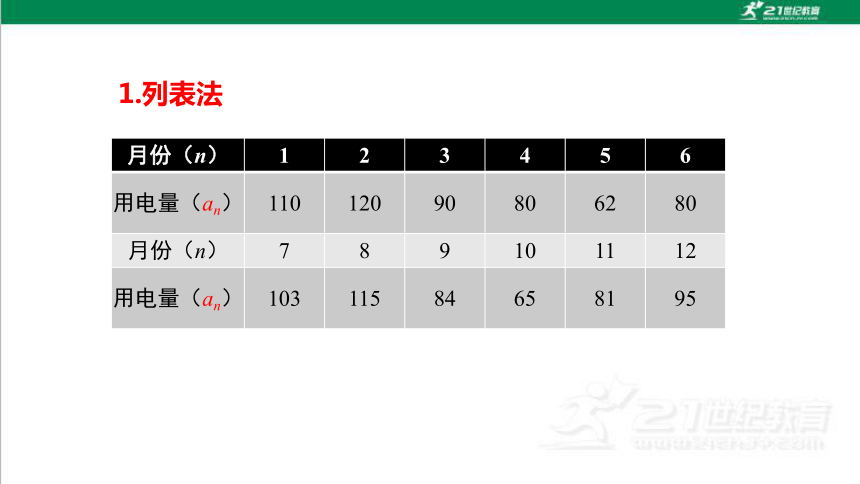
例如,对于数列③110,120,90,80,62,80,103,115,84,65,81,95,我们可以用如下列表的方法来直观地表示:
月份(n) 1 2 3 4 5 6
用电量(an) 110 120 90 80 62 80
月份(n) 7 8 9 10 11 12
用电量(an) 103 115 84 65 81 95
1.列表法
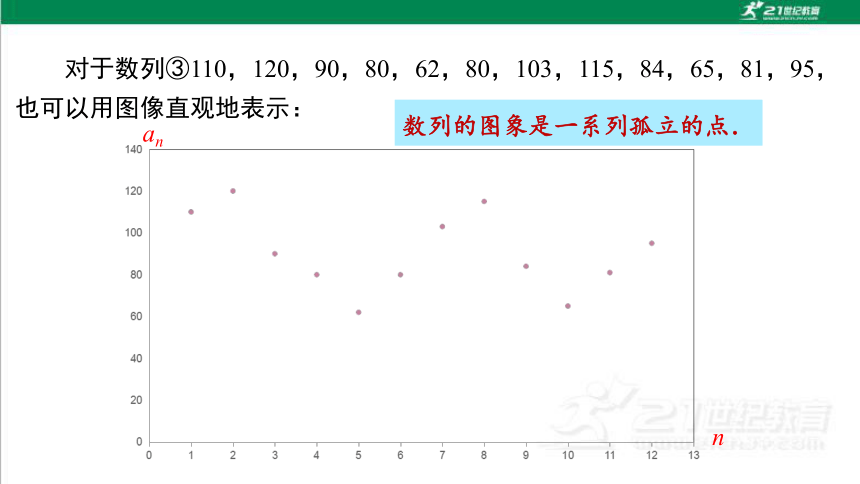
对于数列③110,120,90,80,62,80,103,115,84,65,81,95,也可以用图像直观地表示:
an
n
数列的图象是一系列孤立的点.
从图象上可以清楚地看到,这个家庭哪个月用电量最多,哪个月用电量最少,哪些月用电量在增加,哪些月用电量在减少,用电量随月份的变化也一目了然.
【例1】根据数列{an}的通项公式,写出数列的前5 项及第 n+1项.
用n+1代替通项公式 中的n,得到数列的第 n+1项是 ,
即 .
课本例题
【例1】根据数列{an}的通项公式,写出数列的前5 项及第 n+1项.
【解析】(2)在通项公式中依次取n=1,2,3,4,5,得到数列的前5项
分别为:
用n+1代替通项公式 中的n,
得到数列的第 n+1项是 ,
即 .
课本例题
【解析】(1)因为这个数列的前4项为 3-1,3+1,3-1,3+1,
由此得到它的一个通项公式:
【例2】观察下面各数列,试着找出它的一个通项公式.
(1)2,4,2,4,…;
(2)9,99,999,9 999,…;
课本例题
课本例题
(2)因为这个数列的前4项为10 -1,102 -1,103 -1,104 -1,
由此得到它的一个通项公式:
an=10n-1
(3)因为这个数列的前4项为
, , ,
,
由此得到它的一个通项公式:
思考:根据数列的前若干项写出的通项公式是唯一的吗?试举例说明(例如本节开始所列举的数列④).
典例剖析
题型1 数列的概念和分类
例1 (1)下列说法正确的是( )
A.数列4,7,3,4的首项是4
B.数列{an}中,若a1=3,则从第2项起,各项均不等于3
C.数列3,6,8可以表示为{3,6,8}
D.a,-3,-1,1,b,5,7,9,11一定能构成数列
A
解析:
(1)根据数列的相关概念,可知数列4,7,3,4的第1项就是首项,即4,故A正确;
同一个数在一个数列中可以重复出现,故B错误;
数列和数的顺序有关,集合中元素具有无序性,故C错误;
当a,b都代表数时,能构成数列,当a,b中至少有一个不代表数时,不能构成数列,因为数列是按确定的顺序排列的一列数,故D错误.
典例剖析
①⑤
②③④⑥
数列的判断技巧及分类方法
(1)数列的判断方法
①集合中的数是无序的,元素又是互异的;而数列中的数是严格按照顺序排列的,项与项可以是相同的;
②组成数列的数相同,而且排列次序也相同,满足这两个条件才是相同的数列.
(2)根据数列的项数可分为:
①项数有限的数列是有穷数列;
②项数无限的数列是无穷数列.
概念归纳
练一练
C
典例剖析
题型2 观察法写出数列的通项公式
观察法写出数列的通项公式的策略
概念归纳
练一练
典例剖析
题型3 数列通项公式的简单应用
归纳总结
1.利用数列的通项公式求某项的方法
数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,就可以求出数列的相应项.
2.判断某数值是否为该数列的项的方法
先假定它是数列中的第n项,然后列出关于n的方程.若方程的解为正整数,则是数列的一项;若方程无解或解不是正整数,则不是该数列的一项.
3.已知数列{an}的通项公式是an=2n2-n,n∈N+.
(1)写出数列的前3项;
(2)判断45是否为数列{an}中的项,3是否为数列{an}中的项.
练一练
1.下列说法正确的是( )
A.数列中不能重复出现同一个数
B.1,2,3,4与4,3,2,1是同一数列
C.1,1,1,1不是数列
D.若两个数列的每一项均相同,则这两个数列相同
随堂练
D
随堂练
D
4.数列{an}的通项公式为an= 则a3+a6=_____.
8
3.将数列{2n-1}与{n2}的公共项从小到大排列得到数列{an},
则a3=_____.
25
随堂练
5.判断正误(正确的画“√”,错误的画“×”)
(1){0,1,2,3,4}是有穷数列.( )
(2)数列1,2,3,4和数列1,2,4,3是同一数列.( )
(3)所有自然数能构成数列.( )
(4)数列1,3,5,7,…,2n+1,…的通项公式是an=2n+1.( )
随堂练
×
×
√
×
6.下列有关数列的说法正确的是( )
A.同一数列的任意两项均不可能相同
B.数列-1,0,1与数列1,0,-1是同一个数列
C.数列1,3,5,7可表示为{1,3,5,7}
D.数列中的每一项都与它的序号有关
随堂练
D
B
随堂练
A
错因分析
易错辨析 忽视数列中n∈N+致错
例4 已知数列{an}的通项公式为an=n2-5n+4,则an的最小值为________.
-2
错因分析
出错原因 纠错心得
数列的定义域是正整数集合时,是特殊的函数,所以解题时一定不要忘记n∈N+这一条件.
【易错警示】
1.(多选)下列说法正确的是( )
A.数列可以用图象来表示
B.有些数列的通项公式不唯一
C.数列中的项不能相等
D.数列可以用一群孤立的点表示
ABC
分层练习-基础
2.已知数列{an}的通项公式为an=(-1)n(n2-1),则a6等于( )
A.35 B.-11 C.-35 D.11
A
3.数列-1,3,-7,15,…的一个通项公式可以是( )
A.an=(-1)n·(2n-1),n∈N+
B.an=(-1)n·(2n-1),n∈N+
C.an=(-1)n+1·(2n-1),n∈N+
D.an=(-1)n+1·(2n-1),n∈N+
A
分层练习-基础
分层练习-基础
ABD
分层练习-基础
C
A.第127项 B.第128项
C.第129项 D.第130项
B
12
分层练习-基础
8.在数列1,1,2,3,5,8,x,21,34,55,…中,x=____.
13
9.写出下列各数列的一个通项公式:
(1)4,6,8,10,…;
各项是从4开始的偶数,
所以an=2n+2,n∈N+.
每一项分母可写成21,22,23,24,25,…,分子分别比分母少1,
分层练习-基础
(3)0.3,0.33,0.333,0.333 3,….
分层练习-基础
10.已知数列{an}中,a1=3,a10=21,an是关于项数n的一次函数.
(1)求{an}的通项公式,并求a2 023;
设an=kn+b(k≠0),
∴an=2n+1(n∈N+),
∴a2 023=4 047.
分层练习-基础
(2)若{bn}是由a2,a4,a6,a8,…组成的,试写出{bn}的一个通项公式.
∵a2,a4,a6,a8,…为5,9,13,17,…,
∴bn=4n+1.
分层练习-基础
分层练习-巩固
C
12.已知数列1,2,2,3,3,3,4,4,4,4,…,n,则该数列的第22项为( )
A.6 B.7 C.64 D.65
B
D
分层练习-巩固
分层练习-巩固
15.某少数民族的刺绣有着悠久的历史,图(1),(2),(3),(4)为最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形,则f(6)=_____.
61
分层练习-拓展
f(1)=1=2×1×0+1,
f(2)=1+3+1=2×2×1+1,
f(3)=1+3+5+3+1=2×3×2+1,
f(4)=1+3+5+7+5+3+1=2×4×3+1,
故f(n)=2n(n-1)+1.
当n=6时,f(6)=2×6×5+1=61.
分层练习-拓展
分层练习-拓展
(2)试判断数列{an}中的项是否都在区间(0,1)内.
分层练习-拓展
∴0课堂小结
1.知识清单:
(1)数列的概念与分类.
(2)数列的通项公式.
(3)数列通项公式的简单应用.
2.方法归纳:观察法、归纳法、猜想法.
3.常见误区:
(1)归纳法求数列的通项公式时归纳不全面.
(2)不注意用(-1)n进行调节,不注意分子、分母间的联系.
湘教版2019高一数学(选修一) 第一章 数列
第一课时 数列的概念及其通项公式
1.1 数列的概念
学习目标
(1)理解数列的有关概念和几种简单的表示方法(重点)
(2) 发现数列的规律,找出数列可能的通项公式(难点)
(3)掌握数列通项公式概念及其应用(重点、难点)
情景导入
有人说,大自然是懂数学的,例如树木的分叉、花瓣的数量、植物种子的排列等等,都遵循着某种数学规律,大家能想到它们涉及了哪些数学规律吗?
通过本节课的学习,这些问题都会得到解决.
1.数列的概念
新知探究
在现实世界中,许多事物的数量可以排成一列数.例如:
(1)如下图所示,在超市的货架上摆放有一些罐头,最顶上一层有 2 听罐头,其余每一层的罐头数都比它上面一层的罐头数多 2,共堆了 8 层,则从上到下每层的罐头数依次为:
2,4,6,8,10,12,14,16. ①
(2)《庄子·天下》有一句话:"一尺之棰,日取其半,万世不竭."意思是∶一尺长的木棒,每日取其一半,永远也取不完.这样,每日剩下的部分都是前一天的一半. 如果把"一尺之棰"看成单位"1",那么每日剩下的部分依次为: ②
(4)π,2π,3π,4π,…的正弦值依次为:
0,0,0,0,… ④
(3)某家庭一年内1-12月的用电量(单位∶kW/h)依次为:
110,120,90,80,62,80,103,115,84,65,81,95. ③
(5)正整数1,2,3,4,5,6,…被 3除的余数依次为:
1,2,0,1,2,0,1,2,0,…. ⑤
概念归纳
把这些例子的共同特征抽象出来,得到数列的概念∶
按照一定顺序排成的一列数叫作数列.
数列中的每一个数叫作这个数列的项,排在第一位的数叫作数列的
首项或叫作数列的第1项,排在第二位的数叫作数列的第 2 项,……,
排在第n位的数叫作数列的第n项,所以数列的一般形式可以写成
a1,a2,…,an,… 简记为{an}.
数列分类:
项数有限的数列称为有穷数列,如数列①、③;
项数无限的数列称为无穷数列,如数列②、④、⑤.
上面的数列 ②中,每一项的序号n与对应项an,有如下关系式:
这样,根据以上公式我们可以求出数列②的任意指定的项.
实际上,对任意的数列{an},其每一项的序号与该项都有如下对应关系:
2.数列的表示—通项公式
新知探究
序号
项
1
2
3
4
···
n
···
a1
a2
a3
a4
···
an
···
实际上,对任意的数列{an},其每一项的序号与该项都有如下对应关系:
因此,数列可以看成以正整数集N+(或它的有限子集{1,2,…,n})为定义域的函数an = f (n),当自变量按照从小到大的顺序依次取值时所对应的一列函数值 f (1), f (2), f (3),…..
如果数列{an}的第n项an,可以用关于n的一个公式表示,那么这个公式就称为数列{an}的通项公式.
从函数的观点看,数列的通项公式就是数列的解析表达式.
3.数列的表示 - 列表法
新知探究
例如,数列① 2,4,6,8,10,12,14,16.
② 的一个通项公式分别是:
与函数一样,数列还可以用列表法和图象法来表示.
例如,对于数列③110,120,90,80,62,80,103,115,84,65,81,95,我们可以用如下列表的方法来直观地表示:
月份(n) 1 2 3 4 5 6
用电量(an) 110 120 90 80 62 80
月份(n) 7 8 9 10 11 12
用电量(an) 103 115 84 65 81 95
1.列表法
对于数列③110,120,90,80,62,80,103,115,84,65,81,95,也可以用图像直观地表示:
an
n
数列的图象是一系列孤立的点.
从图象上可以清楚地看到,这个家庭哪个月用电量最多,哪个月用电量最少,哪些月用电量在增加,哪些月用电量在减少,用电量随月份的变化也一目了然.
【例1】根据数列{an}的通项公式,写出数列的前5 项及第 n+1项.
用n+1代替通项公式 中的n,得到数列的第 n+1项是 ,
即 .
课本例题
【例1】根据数列{an}的通项公式,写出数列的前5 项及第 n+1项.
【解析】(2)在通项公式中依次取n=1,2,3,4,5,得到数列的前5项
分别为:
用n+1代替通项公式 中的n,
得到数列的第 n+1项是 ,
即 .
课本例题
【解析】(1)因为这个数列的前4项为 3-1,3+1,3-1,3+1,
由此得到它的一个通项公式:
【例2】观察下面各数列,试着找出它的一个通项公式.
(1)2,4,2,4,…;
(2)9,99,999,9 999,…;
课本例题
课本例题
(2)因为这个数列的前4项为10 -1,102 -1,103 -1,104 -1,
由此得到它的一个通项公式:
an=10n-1
(3)因为这个数列的前4项为
, , ,
,
由此得到它的一个通项公式:
思考:根据数列的前若干项写出的通项公式是唯一的吗?试举例说明(例如本节开始所列举的数列④).
典例剖析
题型1 数列的概念和分类
例1 (1)下列说法正确的是( )
A.数列4,7,3,4的首项是4
B.数列{an}中,若a1=3,则从第2项起,各项均不等于3
C.数列3,6,8可以表示为{3,6,8}
D.a,-3,-1,1,b,5,7,9,11一定能构成数列
A
解析:
(1)根据数列的相关概念,可知数列4,7,3,4的第1项就是首项,即4,故A正确;
同一个数在一个数列中可以重复出现,故B错误;
数列和数的顺序有关,集合中元素具有无序性,故C错误;
当a,b都代表数时,能构成数列,当a,b中至少有一个不代表数时,不能构成数列,因为数列是按确定的顺序排列的一列数,故D错误.
典例剖析
①⑤
②③④⑥
数列的判断技巧及分类方法
(1)数列的判断方法
①集合中的数是无序的,元素又是互异的;而数列中的数是严格按照顺序排列的,项与项可以是相同的;
②组成数列的数相同,而且排列次序也相同,满足这两个条件才是相同的数列.
(2)根据数列的项数可分为:
①项数有限的数列是有穷数列;
②项数无限的数列是无穷数列.
概念归纳
练一练
C
典例剖析
题型2 观察法写出数列的通项公式
观察法写出数列的通项公式的策略
概念归纳
练一练
典例剖析
题型3 数列通项公式的简单应用
归纳总结
1.利用数列的通项公式求某项的方法
数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,就可以求出数列的相应项.
2.判断某数值是否为该数列的项的方法
先假定它是数列中的第n项,然后列出关于n的方程.若方程的解为正整数,则是数列的一项;若方程无解或解不是正整数,则不是该数列的一项.
3.已知数列{an}的通项公式是an=2n2-n,n∈N+.
(1)写出数列的前3项;
(2)判断45是否为数列{an}中的项,3是否为数列{an}中的项.
练一练
1.下列说法正确的是( )
A.数列中不能重复出现同一个数
B.1,2,3,4与4,3,2,1是同一数列
C.1,1,1,1不是数列
D.若两个数列的每一项均相同,则这两个数列相同
随堂练
D
随堂练
D
4.数列{an}的通项公式为an= 则a3+a6=_____.
8
3.将数列{2n-1}与{n2}的公共项从小到大排列得到数列{an},
则a3=_____.
25
随堂练
5.判断正误(正确的画“√”,错误的画“×”)
(1){0,1,2,3,4}是有穷数列.( )
(2)数列1,2,3,4和数列1,2,4,3是同一数列.( )
(3)所有自然数能构成数列.( )
(4)数列1,3,5,7,…,2n+1,…的通项公式是an=2n+1.( )
随堂练
×
×
√
×
6.下列有关数列的说法正确的是( )
A.同一数列的任意两项均不可能相同
B.数列-1,0,1与数列1,0,-1是同一个数列
C.数列1,3,5,7可表示为{1,3,5,7}
D.数列中的每一项都与它的序号有关
随堂练
D
B
随堂练
A
错因分析
易错辨析 忽视数列中n∈N+致错
例4 已知数列{an}的通项公式为an=n2-5n+4,则an的最小值为________.
-2
错因分析
出错原因 纠错心得
数列的定义域是正整数集合时,是特殊的函数,所以解题时一定不要忘记n∈N+这一条件.
【易错警示】
1.(多选)下列说法正确的是( )
A.数列可以用图象来表示
B.有些数列的通项公式不唯一
C.数列中的项不能相等
D.数列可以用一群孤立的点表示
ABC
分层练习-基础
2.已知数列{an}的通项公式为an=(-1)n(n2-1),则a6等于( )
A.35 B.-11 C.-35 D.11
A
3.数列-1,3,-7,15,…的一个通项公式可以是( )
A.an=(-1)n·(2n-1),n∈N+
B.an=(-1)n·(2n-1),n∈N+
C.an=(-1)n+1·(2n-1),n∈N+
D.an=(-1)n+1·(2n-1),n∈N+
A
分层练习-基础
分层练习-基础
ABD
分层练习-基础
C
A.第127项 B.第128项
C.第129项 D.第130项
B
12
分层练习-基础
8.在数列1,1,2,3,5,8,x,21,34,55,…中,x=____.
13
9.写出下列各数列的一个通项公式:
(1)4,6,8,10,…;
各项是从4开始的偶数,
所以an=2n+2,n∈N+.
每一项分母可写成21,22,23,24,25,…,分子分别比分母少1,
分层练习-基础
(3)0.3,0.33,0.333,0.333 3,….
分层练习-基础
10.已知数列{an}中,a1=3,a10=21,an是关于项数n的一次函数.
(1)求{an}的通项公式,并求a2 023;
设an=kn+b(k≠0),
∴an=2n+1(n∈N+),
∴a2 023=4 047.
分层练习-基础
(2)若{bn}是由a2,a4,a6,a8,…组成的,试写出{bn}的一个通项公式.
∵a2,a4,a6,a8,…为5,9,13,17,…,
∴bn=4n+1.
分层练习-基础
分层练习-巩固
C
12.已知数列1,2,2,3,3,3,4,4,4,4,…,n,则该数列的第22项为( )
A.6 B.7 C.64 D.65
B
D
分层练习-巩固
分层练习-巩固
15.某少数民族的刺绣有着悠久的历史,图(1),(2),(3),(4)为最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形,则f(6)=_____.
61
分层练习-拓展
f(1)=1=2×1×0+1,
f(2)=1+3+1=2×2×1+1,
f(3)=1+3+5+3+1=2×3×2+1,
f(4)=1+3+5+7+5+3+1=2×4×3+1,
故f(n)=2n(n-1)+1.
当n=6时,f(6)=2×6×5+1=61.
分层练习-拓展
分层练习-拓展
(2)试判断数列{an}中的项是否都在区间(0,1)内.
分层练习-拓展
∴0
1.知识清单:
(1)数列的概念与分类.
(2)数列的通项公式.
(3)数列通项公式的简单应用.
2.方法归纳:观察法、归纳法、猜想法.
3.常见误区:
(1)归纳法求数列的通项公式时归纳不全面.
(2)不注意用(-1)n进行调节,不注意分子、分母间的联系.
同课章节目录
