湘教版高中数学选择性必修第一册第1章数列1.1数列的概念(第2课时) 课件(共69张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第1章数列1.1数列的概念(第2课时) 课件(共69张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:40:37 | ||
图片预览











文档简介
(共69张PPT)
湘教版2019高一数学(选修一) 第一章 数列
第二课时 数列的递推公式
1.1 数列的概念
学习目标
1.理解递推公式的含义,能根据递推公式求出数列的前几项.
2.了解用累加法、累乘法求通项公式.
3.会由数列的前n项和Sn求数列的通项公式.
4.会求数列的最大(小)项.
情景导入
同学们,前面我们学习了数列的概念以及数列的通项公式,我们知道了数列与现代生活密不可分,其实,当人类祖先需要用一组数据有序地表达一类事物、记录某个变化过程时,数列就应运而生了,因此,数列应用广泛.
问题1 观察如图所示的钢管堆放示意图,你能够发现上下层之间的关系吗?你能否用数列的形式写出上下层之间的关系?
观察可得:
自上而下每一层的钢管数都比上一层的钢管数多1,
即a1=4,a2=5=4+1=a1+1,a3=6=5+1=a2+1.
依此类推:an=an-1+1(2≤n≤7,n∈N+).
1.数列的递推公式
新知探究
例 1.某种生物细胞在实验室的培养过程中,每小时分裂一次(一个分裂为两个),经过12h,由1个这种细胞可以繁殖成多少个细胞
解 设经过n h,这种细胞由 1个可繁殖成an个,细胞的个数形成一个数列{an}.
由题意,细胞每小时分裂一次,得an+1=2an,(n≥1).
由a1=2,并根据an+1=2an,得a2 =4,
依此类推,a3=23,…,a12=212=4 096.
因此经过12 h,这种细胞由1个可繁殖成4 096 个.
像这样,如果数列{an}的任一项an+1与它的前一项an之间的关系可用一个公式来表示,即an+1 =f (an),n≥1,那么这个公式就叫作数列{an}的递推公式;a1称为数列{an}的初始条件.
由递推公式和初始条件可确定数列{an},这是表示数列的又一种重要方法.
许多与数列有关的应用问题最后都归结为这种数学模型,而且这种方法便于计算机编程进行计算.
概念归纳
注意点:
(1)通项公式反映的是an与n之间的关系.
(2)常见的递推关系一般是数列任意两个或三个相邻项之间的推导关系,需要知道首项或前几项,即可求数列中的每一项.
概念归纳
例2(课本例4)根据递推公式和初始条件,
写出数列{an}的前5项,并猜想数列{an}的通项公式.
解 反复利用递推公式,列表如下:
n 1 2 3 4 5 …… n
an 1 ……
3
7
15
31
2n-1
于是,数列{an}的前5项分别是:1,3,7,15,31,
猜想数列{an}的通项公式为2n-1.
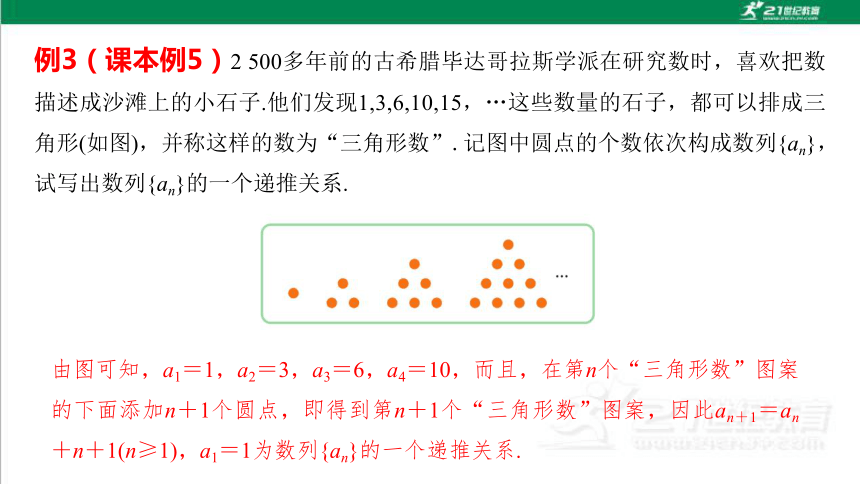
例3(课本例5)2 500多年前的古希腊毕达哥拉斯学派在研究数时,喜欢把数描述成沙滩上的小石子.他们发现1,3,6,10,15,…这些数量的石子,都可以排成三角形(如图),并称这样的数为“三角形数”.记图中圆点的个数依次构成数列{an},试写出数列{an}的一个递推关系.
由图可知,a1=1,a2=3,a3=6,a4=10,而且,在第n个“三角形数”图案的下面添加n+1个圆点,即得到第n+1个“三角形数”图案,因此an+1=an+n+1(n≥1),a1=1为数列{an}的一个递推关系.
2.观察下图,写出点所成数列的一个通项公式.
解 由图可知,
a1=4,a2=7,a3=10,a4=13,……
而且,在第n个图案的添加3个小圆,即得到第n+1个图案,因此,
an+1=an+3(n≥1),a1=4
为数列{an}的一个递推关系.
数列{an}的一个通项公式为:an=3n+1.
课本练习
如果数列{an}的前n项和Sn,与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
我们把数列{an}从第1项到第n项的各项之和,称为数列{an}的前n项和,
常记作Sn,即
数列的前n项和可以看成以正整数集N+(或它的有限子集)为定义域的函数Sn= f (n),当自变量按照从小到大的顺序依次取值时所对应的一列函数值 f (1), f (2), f (3),…..
2.数列的前n项和
新知探究
例4.已知数列{an}的前n项和为Sn,通项公式an=2n-1.
(1) 求S1,S2,S3,S4的值;
(2)猜想数列{an}的前n项和公式Sn;
(3)求Sn-1 (n≥2).
解:(1)依题意,得 S1=a1=1, S2=a1+a2=1+3=4,
S3=a1+a2+a3=1+3+5=9,S4=a1+a2+a3+a4=1+3+5+7=16;
(2)猜想 Sn=n2;
(3)因为Sn=n2,所以用“n-1”替换上式中的“n”,可得Sn-1=(n-1)2.
典例剖析
记数列{an}的前n项和为Sn,通项公式为an,那么an和Sn之间有什么关系呢?
因为Sn=a1+a2+…+an,
所以Sn-1=a1+a2+…+an-1,n≥2,
两式相减,可得
an=Sn-Sn-1,n≥2
又a1=S1,所以
思考探究
例5.已知数列{an}的前n项和公式Sn=n2+n,求数列{an}的通项公式an.
解: 当n≥2时,
an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
又当n=1时,S1=12+1=2,符合上式,
所以数列{an}的通项公式an=2n.
典例剖析
例6.已知数列{an}的前n项和公式Sn=n2-2n-1,求{an}的通项公式an.
解: 当n≥2时,
an=Sn-Sn-1=(n2-2n-1)-[(n-1)2-2(n-1)-1]=2n-3,
又当n=1时,S1=12-2×1-1=-2,不符合上式,
所以数列{an}的通项公式
典例剖析
由数列{an}的前n项和公式Sn求通项公式an:
(1) 当n≥2时,用“n-1”替换Sn中的“n”,求得Sn-1;
(2)两式相减可得an=Sn-Sn-1,n≥2;
(3)将n=1代入Sn,求得a1=S1;
(4)若a1不符合an=Sn-Sn-1,n≥2,则
若a1符合an=Sn-Sn-1,n≥2,则可以把式子统一起来.
概念归纳
概念归纳
数列的递推公式:
如果数列{an}的任一项an+1与它的前一项an之间的关系可用一个公式来表示,即an+1 =f (an),n≥1,那么这个公式就叫作数列{an}的递推公式;a1称为数列{an}的初始条件.
由递推公式和初始条件可确定数列{an},这是表示数列的又一种重要方法.
数列的前n项和公式:
数列{an}从第1项到第n项的各项之和,称为数列{an}的前n项和,常记作Sn,
如果Sn与数列{an}的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列{an}的前n项和公式.
问题1: 我们回顾一下,函数有哪些基本性质呢?
单调性 奇偶性 对称性 周期性 最值 ……
问题2: 数列也是函数,那么数列有哪些基本性质呢?
3.数列的单调性
新知探究
(1)2,4,6,8,10,12,14,16;
(2)
(3)110,120,90,80,62,80,103,115,84,65,81,95;
(4)0,0,0,0,… ;
(5)1,2,0,1,2,0,1,2,0,….
下面,我们先以本节开头给出的5个数列展开分析,类比函数的单调性能否得出数列的单调性的概念呢?
对于数列①,从第 2 项起,每一项都大于它的前一项;
对于数列②,从第 2 项起,每一项都小于它的前一项;
对于数列④,它的每一项都相等;
对于数列③、⑤,从第 2 项起,有些项大于它的前一项,有些项小于它的前一项.
(1)2,4,6,8,10,12,14,16;
(2)
(3)110,120,90,80,62,80,103,115,84,65,81,95;
(4)0,0,0,0,… ;
(5)1,2,0,1,2,0,1,2,0,….
我们可以发现:
概念归纳
一般地,对于一个数列{an},
如果从第2项起,每一项都大于它的前一项,即an+1> an ,那么这个数列叫作递增数列;
如果从第2项起,每一项都小于它的前一项,即an+1< an ,那么这个数列叫作递减数列;
如果各项都相等,即an+1= an ,那么这个数列叫作常数列;
如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,那么这个数列叫作摆动数列.
从数列的图象上看(如下图所示),递增数列的图象是一系列从左至右上升的孤立点,递减数列的图象是一系列从左至右下降的孤立点,摆动数列的图象是一系列从左至右有升有降的孤立点,常数列的图象是一系列从左至右呈水平状的孤立点.
递增数列
递减数列
摆动数列
常数列
例 6 判断下列数列{an}的单调性:
课本例题
例 6 判断下列数列{an}的单调性:
课本例题
要判断数列{an}的单调性,从单调性的定义来看,我们只需比较 an+1与an的大小,而作差法是比较大小常用的一种方法.
例 6 判断下列数列{an}的单调性:
利用函数的单调性也是判断数列{an}的单调性的一种常用方法.
若y=f (x)在[1,+∞)单调递增(或递减),则数列{an}(其中an=f (n))是递增数列(或递减数列).反之不一定成立.
课本例题
课本例题
概念归纳
数列的单调性:
an+1> an 递增数列; an+1< an 递减数列;an+1= an 常数列;
如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,那么这个数列叫作摆动数列.
数列的单调性的判断:
(1)作差法(比较与的大小);
(2)利用数列的通项公式所对的函数的单调性判断.
数列的其他性质:
(1)最值:利用数列的单调性求最值,或求对应函数的最值(注意变量取正整数);
(2)周期性:可以通过列举直观感知数列的周期.
典例剖析
题型1 根据递推公式求数列的项
A
(2)[2022·湖南雅礼中学高二期中]如图①至图④,作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的每一个小三角形中又挖去一个“中心三角形”,以此类推,如果我们用着色三角形代表挖去的部分,那么剩下的白三角形则称为谢尔宾斯基三角形,该概念由波兰数学家谢尔宾斯基在1915年提出.下列4个图形中,若着色三角形的个数依次构成数列{an}的前4项,则a6=________.
364
解析: 依题意可知a1=1,a2=4,a3=13,a4=40,且an+1=3an+1,
所以a5=3a4+1=3×40+1=121,a6=3a5+1=3×121+1=364.
2
练一练
(2)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.结合图形的构成可猜想a2 021-a2 020=________.
2 023
解析: 由题意可知,a1=5,a2=9,a3=14,a4=20,…,
所以,a2-a1=9-5=4=2+2,a3-a2=14-9=5=3+2,
a4-a3=20-14=6=4+2,…
由此我们可以推断:当n≥2时,an-an-1=n+2,
故a2 021-a2 020=2 021+2=2 023.
例2 (1)对于任意数列{an},等式:a1+(a2-a1)+(a3-a2)+…+(an-an-1)=an(n≥2,n∈N+)都成立.试根据这一结论,完成问题:
已知数列{an}满足:a1=1,an+1-an=2,求通项an;
解析:n≥2时,
an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+2+2+…+2(n-1)个2=2(n-1)+1=2n-1.
a1=1也适合上式,
所以数列{an}的通项公式是an=2n-1.
典例剖析
题型2 数列递推公式与通项公式的关系
由数列的递推公式求通项公式的两种方法
归纳总结
A
练一练
典例剖析
题型3 数列单调性的判断
判断数列单调性的四种方法
归纳总结
3.下列数列是递增数列的是( )
A.{1-3n} B.{3n-2n+2}
C.{2n-n} D.{(-3)n}
解析:对于A,令an=1-3n,则a1=-2,a2=-5,不合题意;
对于B,令an=3n-2n+2,则a1=-5,a2=-7,不合题意;
对于C,令an=2n-n,则an+1-an=2n+1-2n-1=2n-1>0,符合题意.
对于D,令an=(-3)n,则a1=-3,a3=-27,不合题意.
练一练
C
典例剖析
题型4 求数列的最大(最小)项
归纳总结
练一练
1.已知在数列{an}中,a1=2,an+1=an+n(n∈N+),则a4的值为( )
A.5 B.6
C.7 D.8
因为a1=2,an+1=an+n,
所以a2=a1+1=2+1=3,
a3=a2+2=3+2=5,
a4=a3+3=5+3=8.
D
随堂练
2.设数列{an}的前n项和为Sn,且Sn=2n-1(n∈N+),则a5等于( )
A.32 B.31
C.16 D.15
当n≥2时,
an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1,
当n=5时,a5=24=16.
随堂练
C
3.已知数列{an}中,a1=1,a2=2,an+an+1+an+2=1,n∈N+,则a2 023等于
( )
A.-2 B.-1 C.1 D.2
∵a1=1,a2=2,an+an+1+an+2=1,
∴a3=1-a1-a2=1-1-2=-2,
a4=1-a3-a2=1-(-2)-2=1,
a5=1-a4-a3=1-1-(-2)=2,
…,
由此推理可得数列{an}是一个周期为3的周期数列,∴a2 023=a1=1.
随堂练
C
4.在数列{an}中,an=n(n-8)-20,n∈N+,则该数列从第_____项开始递增,数列的最小值为______.
故数列{an}从第4项开始递增.
an=n(n-8)-20=(n-4)2-36,根据二次函数的性质知,当n=4时,an取得最小值-36,
即这个数列有最小值,最小值为-36.
-36
4
随堂练
错因分析
1.已知数列{an}的通项公式为an=n2+tn,若数列{an}为递增数列,则t的取值范围是____________.
(-3,+∞)
易错辨析 用函数思想解题时忽略数列的特征而致错
解析:方法一 由数列{an}为递增数列,知
an+1-an=(n+1)2+t(n+1)-(n2+tn)=2n+1+t>0恒成立,
即t>-(2n+1)恒成立.
而n∈N+,所以t>-3,
故t的取值范围是(-3,+∞).
错因分析
【易错警示】
纠错心得:用函数思想解决数列的问题时,特别是研究数列的单调性时,应注意数列的特征.要能够恰当利用函数的性质,通过数形结合来求解
1.已知数列an= ,则该数列是( )
A.递增数列 B.递减数列
C.摆动数列 D.常数列
C
分层练习-基础
2.已知数列{an}满足an=4an-1+3(n≥2,n∈N+),且a1=0,则此数列的第5项是( )
A.15 B.255 C.16 D.63
B
D
分层练习-基础
4.下列给出的图形中,星星的个数构成一个数列,则该数列的一个递推公式可以是( )
A.an+1=an+n,n∈N+
B.an=an-1+n,n∈N+,n≥2
C.an+1=an+(n+1),n∈N+,n≥2
D.an=an-1+(n-1),n∈N+,n≥2
B
5.(多选)已知数列{an}的前n项和满足Sn=2n+1-1,则下列说法正确的是
( )
A.a1=3 B.an=2n(n≥2)
C.an=2n D.an=2n(n≥2)
AD
6.(多选)数列{an}的通项公式为an=n+ ,则( )
A.当a=2时,数列{an}的最小值是a1=a2=3
B.当a=-1时,数列{an}的最小值是a1=0
C.当0D.当a<2时,{an}为递增数列
ABD
分层练习-基础
7.在数列{an}中,an=-2n2+29n+3,则此数列最大项的值是_____.
108
分层练习-基础
8.已知数列{an}中,a1a2…an=n2(n∈N+),则a9=_____.
分层练习-基础
9.已知数列{an}的通项公式为an= (n∈N+),则这个数列是否存在最大
项?若存在,请求出最大项;若不存在,请说明理由.
分层练习-基础
9.已知数列{an}的通项公式为an= (n∈N+),则这个数列是否存在最大
项?若存在,请求出最大项;若不存在,请说明理由.
∴an+110.(1)已知数列{an}的前n项和为Sn,求{an}的通项公式.
①Sn=2n2-3n;
当n=1时,a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1
=2n2-3n-[2(n-1)2-3(n-1)]=4n-5,
当n=1时,a1=-1,符合上式,
所以{an}的通项公式是an=4n-5,n∈N+.
分层练习-基础
②Sn=3n+2;
当n=1时,a1=S1=5,
当n≥2时,an=Sn-Sn-1
=3n+2-(3n-1+2)
=2×3n-1,
当n=1时,a1=5,不符合上式,
分层练习-基础
分层练习-基础
以上n-1个式子左右两边分别相乘,得
分层练习-巩固
11.若数列{an}的通项公式为an= (n∈N+),则这个数列中的最大
项是( )
A.第12项 B.第13项
C.第14项 D.第15项
C
( )
A
13.公元13世纪意大利数学家斐波那契在自己的著作《算盘书》中记载着这样一个数列:1,1,2,3,5,8,13,21,34,…,满足an+2=an+1+an(n≥1),那么1+a2+a4+a6+…+a2 022等于( )
A.a2 021 B.a2 022 C.a2 023 D.a2 024
C
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
15.在一个数列中,如果对任意n∈N+,都有anan+1an+2=k(k为常数),那么这个数列叫作等积数列,k叫作这个数列的公积.已知数列{an}是等积数列,且a1=1,a2=2,公积为8,则a1+a2+a3+…+a12=_____.
依题意得数列{an}是周期为3的数列,
且a1=1,a2=2,a3=4,
因此a1+a2+a3+…+a12=4(a1+a2+a3)=4×(1+2+4)=28.
28
16.已知数列{an}满足:a1=m(m为正整数),an+1=
若a4=4,求m所有可能的取值.
若a3为奇数,则3a3+1=4,a3=1.
若a2为奇数,则3a2+1=1,a2=0(舍去),
分层练习-拓展
若a1为奇数,则3a1+1=16,a1=5,
故m所有可能的取值为4,5,32.
分层练习-拓展
17.[2022·湖南怀化高二期末]历史上数列的发展,折射出许多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,89,…即F(1)=F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3,n∈N+),此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列{bn},又记数列{cn}满足c1=b1,c2=b2,cn=bn-bn-1(n≥3,n∈N+),则c1+c2+c3+…+c2 021的值为( )
A.4 B.-728
C.2 D.3
分层练习-拓展
C
解析:由题意可知,{bn}为1,1,2,3,1,0,1,1,2,3,1,0,1,1…周期为6的数列,{cn}为1,1,1,1,-2,-1,1,0,1,1,-2,-1,1,0是从第三项起周期为6的数列.
从第3项起,每一个周期的6个数的和是1+1+(-2)+(-1)+1+0=0,
所以c1+c2+c3+…+c2 021=c1+c2+0×336+c2 019+c2 020+c2 021=1+1+0+1+1+(-2)=2.
分层练习-拓展
1.知识清单:
(1)数列的概念与分类.
(2)数列的通项公式.
(3)数列通项公式的简单应用.
(4)数列的递推公式.
(5)由递推公式求通项公式.
(6)数列的前n项和Sn与an的关系.
(7)数列的单调性及最大(小)项.
课堂小结
课堂小结
2.方法归纳:归纳法、观察法、猜想法、迭代法、累加法、累乘法.
3.常见误区:
(1)归纳法求数列的通项公式时归纳不全面.
(2)不注意用(-1)n进行调节,不注意分子、分母间的联系.
(3)累加法、累乘法中不注意验证首项是否符合通项公式.
(4)由Sn求an时忽略验证n=1时的情况.
湘教版2019高一数学(选修一) 第一章 数列
第二课时 数列的递推公式
1.1 数列的概念
学习目标
1.理解递推公式的含义,能根据递推公式求出数列的前几项.
2.了解用累加法、累乘法求通项公式.
3.会由数列的前n项和Sn求数列的通项公式.
4.会求数列的最大(小)项.
情景导入
同学们,前面我们学习了数列的概念以及数列的通项公式,我们知道了数列与现代生活密不可分,其实,当人类祖先需要用一组数据有序地表达一类事物、记录某个变化过程时,数列就应运而生了,因此,数列应用广泛.
问题1 观察如图所示的钢管堆放示意图,你能够发现上下层之间的关系吗?你能否用数列的形式写出上下层之间的关系?
观察可得:
自上而下每一层的钢管数都比上一层的钢管数多1,
即a1=4,a2=5=4+1=a1+1,a3=6=5+1=a2+1.
依此类推:an=an-1+1(2≤n≤7,n∈N+).
1.数列的递推公式
新知探究
例 1.某种生物细胞在实验室的培养过程中,每小时分裂一次(一个分裂为两个),经过12h,由1个这种细胞可以繁殖成多少个细胞
解 设经过n h,这种细胞由 1个可繁殖成an个,细胞的个数形成一个数列{an}.
由题意,细胞每小时分裂一次,得an+1=2an,(n≥1).
由a1=2,并根据an+1=2an,得a2 =4,
依此类推,a3=23,…,a12=212=4 096.
因此经过12 h,这种细胞由1个可繁殖成4 096 个.
像这样,如果数列{an}的任一项an+1与它的前一项an之间的关系可用一个公式来表示,即an+1 =f (an),n≥1,那么这个公式就叫作数列{an}的递推公式;a1称为数列{an}的初始条件.
由递推公式和初始条件可确定数列{an},这是表示数列的又一种重要方法.
许多与数列有关的应用问题最后都归结为这种数学模型,而且这种方法便于计算机编程进行计算.
概念归纳
注意点:
(1)通项公式反映的是an与n之间的关系.
(2)常见的递推关系一般是数列任意两个或三个相邻项之间的推导关系,需要知道首项或前几项,即可求数列中的每一项.
概念归纳
例2(课本例4)根据递推公式和初始条件,
写出数列{an}的前5项,并猜想数列{an}的通项公式.
解 反复利用递推公式,列表如下:
n 1 2 3 4 5 …… n
an 1 ……
3
7
15
31
2n-1
于是,数列{an}的前5项分别是:1,3,7,15,31,
猜想数列{an}的通项公式为2n-1.
例3(课本例5)2 500多年前的古希腊毕达哥拉斯学派在研究数时,喜欢把数描述成沙滩上的小石子.他们发现1,3,6,10,15,…这些数量的石子,都可以排成三角形(如图),并称这样的数为“三角形数”.记图中圆点的个数依次构成数列{an},试写出数列{an}的一个递推关系.
由图可知,a1=1,a2=3,a3=6,a4=10,而且,在第n个“三角形数”图案的下面添加n+1个圆点,即得到第n+1个“三角形数”图案,因此an+1=an+n+1(n≥1),a1=1为数列{an}的一个递推关系.
2.观察下图,写出点所成数列的一个通项公式.
解 由图可知,
a1=4,a2=7,a3=10,a4=13,……
而且,在第n个图案的添加3个小圆,即得到第n+1个图案,因此,
an+1=an+3(n≥1),a1=4
为数列{an}的一个递推关系.
数列{an}的一个通项公式为:an=3n+1.
课本练习
如果数列{an}的前n项和Sn,与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
我们把数列{an}从第1项到第n项的各项之和,称为数列{an}的前n项和,
常记作Sn,即
数列的前n项和可以看成以正整数集N+(或它的有限子集)为定义域的函数Sn= f (n),当自变量按照从小到大的顺序依次取值时所对应的一列函数值 f (1), f (2), f (3),…..
2.数列的前n项和
新知探究
例4.已知数列{an}的前n项和为Sn,通项公式an=2n-1.
(1) 求S1,S2,S3,S4的值;
(2)猜想数列{an}的前n项和公式Sn;
(3)求Sn-1 (n≥2).
解:(1)依题意,得 S1=a1=1, S2=a1+a2=1+3=4,
S3=a1+a2+a3=1+3+5=9,S4=a1+a2+a3+a4=1+3+5+7=16;
(2)猜想 Sn=n2;
(3)因为Sn=n2,所以用“n-1”替换上式中的“n”,可得Sn-1=(n-1)2.
典例剖析
记数列{an}的前n项和为Sn,通项公式为an,那么an和Sn之间有什么关系呢?
因为Sn=a1+a2+…+an,
所以Sn-1=a1+a2+…+an-1,n≥2,
两式相减,可得
an=Sn-Sn-1,n≥2
又a1=S1,所以
思考探究
例5.已知数列{an}的前n项和公式Sn=n2+n,求数列{an}的通项公式an.
解: 当n≥2时,
an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
又当n=1时,S1=12+1=2,符合上式,
所以数列{an}的通项公式an=2n.
典例剖析
例6.已知数列{an}的前n项和公式Sn=n2-2n-1,求{an}的通项公式an.
解: 当n≥2时,
an=Sn-Sn-1=(n2-2n-1)-[(n-1)2-2(n-1)-1]=2n-3,
又当n=1时,S1=12-2×1-1=-2,不符合上式,
所以数列{an}的通项公式
典例剖析
由数列{an}的前n项和公式Sn求通项公式an:
(1) 当n≥2时,用“n-1”替换Sn中的“n”,求得Sn-1;
(2)两式相减可得an=Sn-Sn-1,n≥2;
(3)将n=1代入Sn,求得a1=S1;
(4)若a1不符合an=Sn-Sn-1,n≥2,则
若a1符合an=Sn-Sn-1,n≥2,则可以把式子统一起来.
概念归纳
概念归纳
数列的递推公式:
如果数列{an}的任一项an+1与它的前一项an之间的关系可用一个公式来表示,即an+1 =f (an),n≥1,那么这个公式就叫作数列{an}的递推公式;a1称为数列{an}的初始条件.
由递推公式和初始条件可确定数列{an},这是表示数列的又一种重要方法.
数列的前n项和公式:
数列{an}从第1项到第n项的各项之和,称为数列{an}的前n项和,常记作Sn,
如果Sn与数列{an}的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列{an}的前n项和公式.
问题1: 我们回顾一下,函数有哪些基本性质呢?
单调性 奇偶性 对称性 周期性 最值 ……
问题2: 数列也是函数,那么数列有哪些基本性质呢?
3.数列的单调性
新知探究
(1)2,4,6,8,10,12,14,16;
(2)
(3)110,120,90,80,62,80,103,115,84,65,81,95;
(4)0,0,0,0,… ;
(5)1,2,0,1,2,0,1,2,0,….
下面,我们先以本节开头给出的5个数列展开分析,类比函数的单调性能否得出数列的单调性的概念呢?
对于数列①,从第 2 项起,每一项都大于它的前一项;
对于数列②,从第 2 项起,每一项都小于它的前一项;
对于数列④,它的每一项都相等;
对于数列③、⑤,从第 2 项起,有些项大于它的前一项,有些项小于它的前一项.
(1)2,4,6,8,10,12,14,16;
(2)
(3)110,120,90,80,62,80,103,115,84,65,81,95;
(4)0,0,0,0,… ;
(5)1,2,0,1,2,0,1,2,0,….
我们可以发现:
概念归纳
一般地,对于一个数列{an},
如果从第2项起,每一项都大于它的前一项,即an+1> an ,那么这个数列叫作递增数列;
如果从第2项起,每一项都小于它的前一项,即an+1< an ,那么这个数列叫作递减数列;
如果各项都相等,即an+1= an ,那么这个数列叫作常数列;
如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,那么这个数列叫作摆动数列.
从数列的图象上看(如下图所示),递增数列的图象是一系列从左至右上升的孤立点,递减数列的图象是一系列从左至右下降的孤立点,摆动数列的图象是一系列从左至右有升有降的孤立点,常数列的图象是一系列从左至右呈水平状的孤立点.
递增数列
递减数列
摆动数列
常数列
例 6 判断下列数列{an}的单调性:
课本例题
例 6 判断下列数列{an}的单调性:
课本例题
要判断数列{an}的单调性,从单调性的定义来看,我们只需比较 an+1与an的大小,而作差法是比较大小常用的一种方法.
例 6 判断下列数列{an}的单调性:
利用函数的单调性也是判断数列{an}的单调性的一种常用方法.
若y=f (x)在[1,+∞)单调递增(或递减),则数列{an}(其中an=f (n))是递增数列(或递减数列).反之不一定成立.
课本例题
课本例题
概念归纳
数列的单调性:
an+1> an 递增数列; an+1< an 递减数列;an+1= an 常数列;
如果从第2项起,有些项大于它的前一项,有些项小于它的前一项,那么这个数列叫作摆动数列.
数列的单调性的判断:
(1)作差法(比较与的大小);
(2)利用数列的通项公式所对的函数的单调性判断.
数列的其他性质:
(1)最值:利用数列的单调性求最值,或求对应函数的最值(注意变量取正整数);
(2)周期性:可以通过列举直观感知数列的周期.
典例剖析
题型1 根据递推公式求数列的项
A
(2)[2022·湖南雅礼中学高二期中]如图①至图④,作一个正三角形,挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的每一个小三角形中又挖去一个“中心三角形”,以此类推,如果我们用着色三角形代表挖去的部分,那么剩下的白三角形则称为谢尔宾斯基三角形,该概念由波兰数学家谢尔宾斯基在1915年提出.下列4个图形中,若着色三角形的个数依次构成数列{an}的前4项,则a6=________.
364
解析: 依题意可知a1=1,a2=4,a3=13,a4=40,且an+1=3an+1,
所以a5=3a4+1=3×40+1=121,a6=3a5+1=3×121+1=364.
2
练一练
(2)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.结合图形的构成可猜想a2 021-a2 020=________.
2 023
解析: 由题意可知,a1=5,a2=9,a3=14,a4=20,…,
所以,a2-a1=9-5=4=2+2,a3-a2=14-9=5=3+2,
a4-a3=20-14=6=4+2,…
由此我们可以推断:当n≥2时,an-an-1=n+2,
故a2 021-a2 020=2 021+2=2 023.
例2 (1)对于任意数列{an},等式:a1+(a2-a1)+(a3-a2)+…+(an-an-1)=an(n≥2,n∈N+)都成立.试根据这一结论,完成问题:
已知数列{an}满足:a1=1,an+1-an=2,求通项an;
解析:n≥2时,
an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+2+2+…+2(n-1)个2=2(n-1)+1=2n-1.
a1=1也适合上式,
所以数列{an}的通项公式是an=2n-1.
典例剖析
题型2 数列递推公式与通项公式的关系
由数列的递推公式求通项公式的两种方法
归纳总结
A
练一练
典例剖析
题型3 数列单调性的判断
判断数列单调性的四种方法
归纳总结
3.下列数列是递增数列的是( )
A.{1-3n} B.{3n-2n+2}
C.{2n-n} D.{(-3)n}
解析:对于A,令an=1-3n,则a1=-2,a2=-5,不合题意;
对于B,令an=3n-2n+2,则a1=-5,a2=-7,不合题意;
对于C,令an=2n-n,则an+1-an=2n+1-2n-1=2n-1>0,符合题意.
对于D,令an=(-3)n,则a1=-3,a3=-27,不合题意.
练一练
C
典例剖析
题型4 求数列的最大(最小)项
归纳总结
练一练
1.已知在数列{an}中,a1=2,an+1=an+n(n∈N+),则a4的值为( )
A.5 B.6
C.7 D.8
因为a1=2,an+1=an+n,
所以a2=a1+1=2+1=3,
a3=a2+2=3+2=5,
a4=a3+3=5+3=8.
D
随堂练
2.设数列{an}的前n项和为Sn,且Sn=2n-1(n∈N+),则a5等于( )
A.32 B.31
C.16 D.15
当n≥2时,
an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1,
当n=5时,a5=24=16.
随堂练
C
3.已知数列{an}中,a1=1,a2=2,an+an+1+an+2=1,n∈N+,则a2 023等于
( )
A.-2 B.-1 C.1 D.2
∵a1=1,a2=2,an+an+1+an+2=1,
∴a3=1-a1-a2=1-1-2=-2,
a4=1-a3-a2=1-(-2)-2=1,
a5=1-a4-a3=1-1-(-2)=2,
…,
由此推理可得数列{an}是一个周期为3的周期数列,∴a2 023=a1=1.
随堂练
C
4.在数列{an}中,an=n(n-8)-20,n∈N+,则该数列从第_____项开始递增,数列的最小值为______.
故数列{an}从第4项开始递增.
an=n(n-8)-20=(n-4)2-36,根据二次函数的性质知,当n=4时,an取得最小值-36,
即这个数列有最小值,最小值为-36.
-36
4
随堂练
错因分析
1.已知数列{an}的通项公式为an=n2+tn,若数列{an}为递增数列,则t的取值范围是____________.
(-3,+∞)
易错辨析 用函数思想解题时忽略数列的特征而致错
解析:方法一 由数列{an}为递增数列,知
an+1-an=(n+1)2+t(n+1)-(n2+tn)=2n+1+t>0恒成立,
即t>-(2n+1)恒成立.
而n∈N+,所以t>-3,
故t的取值范围是(-3,+∞).
错因分析
【易错警示】
纠错心得:用函数思想解决数列的问题时,特别是研究数列的单调性时,应注意数列的特征.要能够恰当利用函数的性质,通过数形结合来求解
1.已知数列an= ,则该数列是( )
A.递增数列 B.递减数列
C.摆动数列 D.常数列
C
分层练习-基础
2.已知数列{an}满足an=4an-1+3(n≥2,n∈N+),且a1=0,则此数列的第5项是( )
A.15 B.255 C.16 D.63
B
D
分层练习-基础
4.下列给出的图形中,星星的个数构成一个数列,则该数列的一个递推公式可以是( )
A.an+1=an+n,n∈N+
B.an=an-1+n,n∈N+,n≥2
C.an+1=an+(n+1),n∈N+,n≥2
D.an=an-1+(n-1),n∈N+,n≥2
B
5.(多选)已知数列{an}的前n项和满足Sn=2n+1-1,则下列说法正确的是
( )
A.a1=3 B.an=2n(n≥2)
C.an=2n D.an=2n(n≥2)
AD
6.(多选)数列{an}的通项公式为an=n+ ,则( )
A.当a=2时,数列{an}的最小值是a1=a2=3
B.当a=-1时,数列{an}的最小值是a1=0
C.当0
ABD
分层练习-基础
7.在数列{an}中,an=-2n2+29n+3,则此数列最大项的值是_____.
108
分层练习-基础
8.已知数列{an}中,a1a2…an=n2(n∈N+),则a9=_____.
分层练习-基础
9.已知数列{an}的通项公式为an= (n∈N+),则这个数列是否存在最大
项?若存在,请求出最大项;若不存在,请说明理由.
分层练习-基础
9.已知数列{an}的通项公式为an= (n∈N+),则这个数列是否存在最大
项?若存在,请求出最大项;若不存在,请说明理由.
∴an+1
①Sn=2n2-3n;
当n=1时,a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1
=2n2-3n-[2(n-1)2-3(n-1)]=4n-5,
当n=1时,a1=-1,符合上式,
所以{an}的通项公式是an=4n-5,n∈N+.
分层练习-基础
②Sn=3n+2;
当n=1时,a1=S1=5,
当n≥2时,an=Sn-Sn-1
=3n+2-(3n-1+2)
=2×3n-1,
当n=1时,a1=5,不符合上式,
分层练习-基础
分层练习-基础
以上n-1个式子左右两边分别相乘,得
分层练习-巩固
11.若数列{an}的通项公式为an= (n∈N+),则这个数列中的最大
项是( )
A.第12项 B.第13项
C.第14项 D.第15项
C
( )
A
13.公元13世纪意大利数学家斐波那契在自己的著作《算盘书》中记载着这样一个数列:1,1,2,3,5,8,13,21,34,…,满足an+2=an+1+an(n≥1),那么1+a2+a4+a6+…+a2 022等于( )
A.a2 021 B.a2 022 C.a2 023 D.a2 024
C
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
15.在一个数列中,如果对任意n∈N+,都有anan+1an+2=k(k为常数),那么这个数列叫作等积数列,k叫作这个数列的公积.已知数列{an}是等积数列,且a1=1,a2=2,公积为8,则a1+a2+a3+…+a12=_____.
依题意得数列{an}是周期为3的数列,
且a1=1,a2=2,a3=4,
因此a1+a2+a3+…+a12=4(a1+a2+a3)=4×(1+2+4)=28.
28
16.已知数列{an}满足:a1=m(m为正整数),an+1=
若a4=4,求m所有可能的取值.
若a3为奇数,则3a3+1=4,a3=1.
若a2为奇数,则3a2+1=1,a2=0(舍去),
分层练习-拓展
若a1为奇数,则3a1+1=16,a1=5,
故m所有可能的取值为4,5,32.
分层练习-拓展
17.[2022·湖南怀化高二期末]历史上数列的发展,折射出许多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,89,…即F(1)=F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3,n∈N+),此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列{bn},又记数列{cn}满足c1=b1,c2=b2,cn=bn-bn-1(n≥3,n∈N+),则c1+c2+c3+…+c2 021的值为( )
A.4 B.-728
C.2 D.3
分层练习-拓展
C
解析:由题意可知,{bn}为1,1,2,3,1,0,1,1,2,3,1,0,1,1…周期为6的数列,{cn}为1,1,1,1,-2,-1,1,0,1,1,-2,-1,1,0是从第三项起周期为6的数列.
从第3项起,每一个周期的6个数的和是1+1+(-2)+(-1)+1+0=0,
所以c1+c2+c3+…+c2 021=c1+c2+0×336+c2 019+c2 020+c2 021=1+1+0+1+1+(-2)=2.
分层练习-拓展
1.知识清单:
(1)数列的概念与分类.
(2)数列的通项公式.
(3)数列通项公式的简单应用.
(4)数列的递推公式.
(5)由递推公式求通项公式.
(6)数列的前n项和Sn与an的关系.
(7)数列的单调性及最大(小)项.
课堂小结
课堂小结
2.方法归纳:归纳法、观察法、猜想法、迭代法、累加法、累乘法.
3.常见误区:
(1)归纳法求数列的通项公式时归纳不全面.
(2)不注意用(-1)n进行调节,不注意分子、分母间的联系.
(3)累加法、累乘法中不注意验证首项是否符合通项公式.
(4)由Sn求an时忽略验证n=1时的情况.
同课章节目录
