湘教版高中数学选择性必修第一册第1章数列1.2.3等差数列的前n项和课件(共72张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第1章数列1.2.3等差数列的前n项和课件(共72张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:40:55 | ||
图片预览










文档简介
(共72张PPT)
湘教版2019高一数学(选修一) 第一章 数列
1.2.3 等差数列的前n项和
1.2 等差数列
学习目标
1.掌握等差数列前n项和公式及其获取思路.
2.熟练掌握等差数列的五个量a1,d,n,an,Sn的关系,能够由其中任意三个求另外两个.
3.能用an与Sn的关系求an.
4.会利用等差数列前n项和的性质简化求和运算.
5.会利用等差数列前n项和的函数特征求最值.
情景导入
高斯(1777-1855),德国著名数学家、物理学家、天文学家,是近代数学的奠基人之一,享有“数学王子”的美誉.高斯7岁时,有一天老师在黑板上出一道题“1+2+3+4+5+…+100=?”对全班同学说:“你们算一算从1开始一直加到100的和是多少?”,同学们不约而同地拿出笔在小石板上沙沙地算起来.不到一分钟,高斯站起来说:“老师,我算出结果来了,是5 050!”老师和其他同学都很吃惊.你知道高斯是怎样快速计算出来的吗?
1.等差数列的前 n 项和
新知探究
被世人誉为"数学王子"的德国数学家高斯在幼年就显示出过人的数学天赋,他的老师布置了一道看上去很难的题,计算1+2+3+...+100=?高斯经过细致的观察,迅捷地报出了得数:5 050.
在老师与同学露出惊讶之色时,他解释了自己的思考过程:
将这 100个数分成 50 个数对,其中1+100=101,2+99=101,…, 50+51=101,于是 100 个数的和就是 50 个101,即 50× 101=5 050.
高斯的算法实际上解决了求等差数列1,2,3,…,n, …前100项之和的问题.
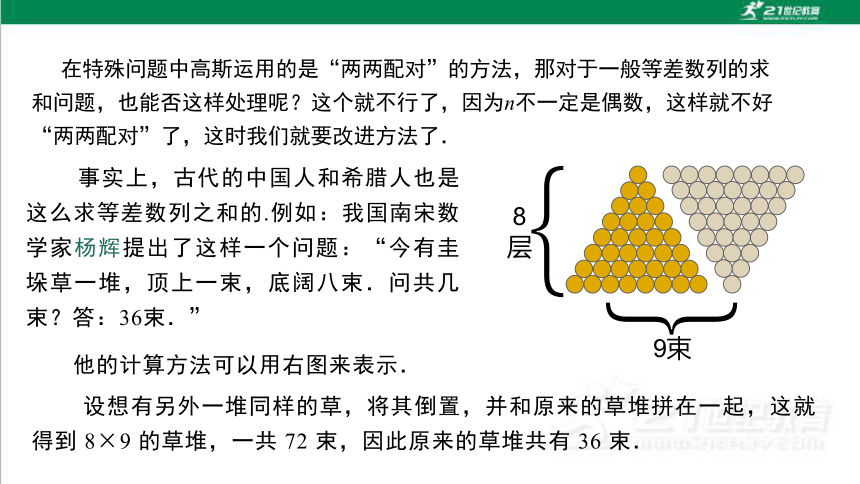
事实上,古代的中国人和希腊人也是这么求等差数列之和的.例如:我国南宋数学家杨辉提出了这样一个问题:“今有圭垛草一堆,顶上一束,底阔八束.问共几束?答:36束.”
8层
{
{
9束
他的计算方法可以用右图来表示.
设想有另外一堆同样的草,将其倒置,并和原来的草堆拼在一起,这就得到 8×9 的草堆,一共 72 束,因此原来的草堆共有 36 束.
在特殊问题中高斯运用的是“两两配对”的方法,那对于一般等差数列的求和问题,也能否这样处理呢?这个就不行了,因为n不一定是偶数,这样就不好“两两配对”了,这时我们就要改进方法了.
前人计算等差数列前n项和的方法的确巧妙,那么这种方法能推广到求一般等差数列的前n项和吗?
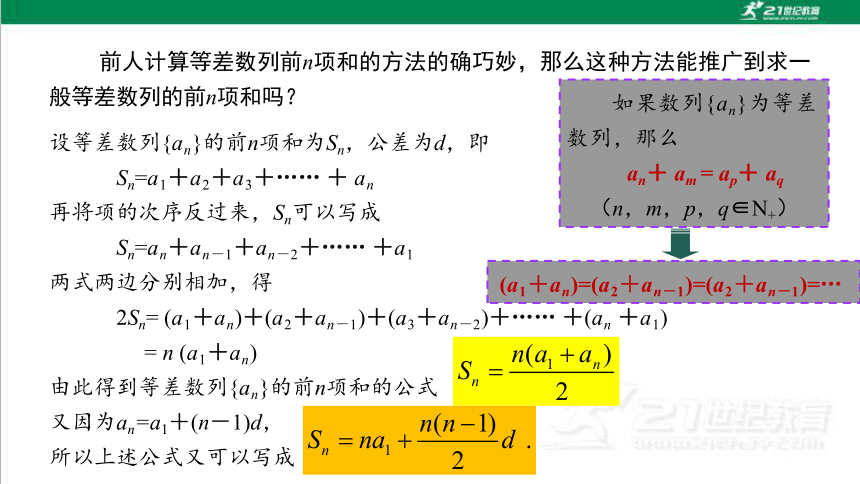
设等差数列{an}的前n项和为Sn,公差为d,即
Sn=a1+a2+a3+…… + an
再将项的次序反过来,Sn可以写成
Sn=an+an-1+an-2+…… +a1
两式两边分别相加,得
2Sn= (a1+an)+(a2+an-1)+(a3+an-2)+…… +(an +a1)
= n (a1+an)
由此得到等差数列{an}的前n项和的公式
又因为an=a1+(n-1)d,
所以上述公式又可以写成
如果数列{an}为等差数列,那么
an+ am = ap+ aq
(n,m,p,q∈N+)
(a1+an)=(a2+an-1)=(a2+an-1)=…
这个公式表明,等差数列的前n项和可由首项、公差和项数唯一确定.
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个
量,故知三可求其二.
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
概念归纳
例 7 某体育馆一角的看台上有20排,每一排比前一排多两个座位,若第一排有15个座位,则体育馆一角里共有多少个座位?
解: 设第n排的座位有an个,
则得到的数列{an}(1≤n≤20)是首项为15,公差为2的等差数列.
根据等差数列前n项和公式,
这一角里总共的座位数为
课本例题
课本例题
例 8 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
解: 记该数列为{an},公差为d,
根据等差数列前n项和公式,可得
S10=10a1+45d =310,S20=20a1+190d =1220,
解得a1=4,d =6,
因此该等差数列的前n项和为
解: 因为Sn=n2+2n,
所以当n ≥2 时,有
an=Sn-Sn-1
=(n2+2n)-[(n-1)2+2(n-1)]
=2n+1,
又当n=1时,a1=S1=12+2=3,符合上式,
所以数列{an}的通项公式an=2n+1.
当n ≥2 时,有an-an-1=(2n+1)-[2(n-1)+1]=2,
所以数列{an}是以3为首项,以2为公差的等差数列.
设等差数列{an}的前n项和为Sn,
则
所以等差数列的前n项和公式Sn可以看成关于n的二次函数(常数项为0).
例 9 设数列{an}的前n项和Sn=n2+2n,求证:{an}是等差数列.
课本例题
例10 已知Sn为等差数列{an}的前n项和,且a1=25,S17=S9.
(1)求数列{an}的通项公式;
(2)求 Sn的最大值及对应的n值.
解: (1)记数列{an}的公差为d,由S17=S9,可得
17a1+136d =9a1+36d ,
又a1=25,解得d =-2,
所以an=25+(n-1)ⅹ(-2)=27-2n.
课本例题
例10 已知Sn为等差数列{an}的前n项和,且a1=25,S17=S9.
(1)求数列{an}的通项公式; an=27-2n
(2)求Sn的最大值及对应的n值.
解: (2)因为
所以当n=13 时,Sn取最大值,S13=169.
解: (2)令an=27-2n>0,得n<13.5
即当n≤13时,an>0,当n≥14时,an<0,
故当n=13 时,Sn取最大值,S13=13ⅹ25+78ⅹ(-2)=169.
课本例题
已知等差数列{an}的前n项和为Sn.
(1)求证:S2,S4-S2,S6-S4成等差数列;
(2)求证:S3,S6-S3,S9-S6 成等差数列;
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
证明:记数列{an}的公差为d,
因为S2 = a1+a2,S4-S2 = a3+a4,S6-S4 = a5+a6,
所以(S4-S2)-S2 = (a3+a4)-(a1+a2) = 4d,
(S6-S4)-(S4-S2) = (a5+a6)-(a3+a4) = 4d,
即 (S6-S4)-(S4-S2) = (S4-S2)-S2,
所以S2,S4-S2,S6-S4成等差数列.
思考探究
已知等差数列{an}的前n项和为Sn.
(1)求证:S2,S4-S2,S6-S4成等差数列;
(2)求证:S3,S6-S3,S9-S6 成等差数列;
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
证明:记数列{an}的公差为d,
因为S3 = a1+a2+a3,S6-S3 = a4+a5+a6,S9-S6 = a7+a8+a9,
所以(S6-S3)-S3 = (a4+a5+a6)-(a1+a2+a3) = 9d,
(S9-S6 )-(S6-S3) = (a7+a8+a9)-(a4+a5+a6) = 9d,
即 (S9-S6 )-(S6-S3) = (S6-S3)-S3,
所以S3,S6-S3,S9-S6成等差数列.
思考探究
已知等差数列{an}的前n项和为Sn,.
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
猜想:Sm,S2m-Sm,S3m-S2m成等差数列.
证明:因为Sm = a1+a2+……+am,
S2m-Sm = am+1+ am+2+……+a2m,
S3m-S2m = a2m+1+ a2m+2+……+a3m,
所以(S2m-Sm)-Sm =m2d,
(S3m-S2m)-(S2m-Sm)==m2d,
即 (S3m-S2m)-(S2m-Sm) = (S2m-Sm)-Sm,
所以Sm,S2m-Sm,S3m-S2m成等差数列.
思考探究
1.若在等差数列{an}中,有a1+a4+a7=10,a3+a6+a9=22,
则a2+a5+a8= .
解:记数列{an}的公差为d,
因为(a3+a6+a9)-(a1+a4+a7)
=(a3-a1)+ (a6-a4)+(a9-a7)
=6d =12,
所以 d =2,
所以a2+a5+a8=(a1+d)+(a4+d)+(a7+d)=(a1+a4+a7)+3d =16.
练一练
概念归纳
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
等差数列的前n项和公式Sn可以看成关于n的二次函数(常数项为0).
若等差数列的前n项和为Sn,则Sm,S2m-Sm,S3m-S2m成等差数列.
题型1 等差数列前n项和的基本计算
典例剖析
(2)已知a1=4,S8=172,求a8和d;
(3)已知d=2,an=11,Sn=35,求a1和n.
等差数列中基本计算的两个技巧
(1)利用基本量求值
(2)利用等差数列的性质解题
归纳总结
练一练
C
-4
练一练
解析:由题意知,该地区9月份前10天流感病毒的新感染者人数,
构成一个首项a1=40,公差d=40的等差数列,
所以9月10日的新感染者人数为a10=40+(10-1)×40=400(人),
所以9月11日的新感染者人数为a11=400-10=390(人);
例2 某地去年9月份曾发生流感,据统计,9月1日该地区流感病毒的新感染者有40人,此后,每天的新感染者人数比前一天新感染者人数增加40.从9月11日起,该地区医疗部门采取措施,使该种病毒的传播得到有效控制,每天的新感染者人数比前一天的新感染者人数减少10.
(1)分别求出该地区在9月10日和9月11日这两天的流感病毒的新感染者人数;
题型2 等差数列前n项和公式的实际应用
典例剖析
(2)该地区9月份(共30天)流感病毒的新感染者共有多少人?
归纳总结
(1)解答与等差数列前n项和有关的应用题,其关键在于构造合适的等差数列.
(2)遇到与正整数有关的应用题时,可以考虑与数列知识联系,建立数列模型,具体解决要注意以下两点:
①抓住实际问题的特征,明确是什么类型的数列模型.
②深入分析题意,确定是求通项公式an,或是求前n项和Sn,还是求项数n.
3.[2022·湖南部分重点中学联考]跑步是一项有氧运动,通过跑步,我们能提高肌力,同时提高体内的基础代谢水平,加速脂肪的燃烧,养成易瘦体质.小林最近给自己制定了一个200千米的跑步健身计划,他第一天跑了8千米,以后每天比前一天多跑0.5千米,则他要完成该计划至少需要( )
A.16天 B.17天 C.18天 D.19天
练一练
B
解析:由等差数列{an}的性质,
.可得Sm,S2m-Sm,S3m-S2m成等差数列,
即30,70,S3m-100成等差数列,
所以2×70=30+S3m-100,解得S3m=210.
例3 (1)等差数列{an}的前m项和为30,前2m项和为100,求数列{an}的前3m项的和S3m;
题型3 等差数列前n项和性质的应用
典例剖析
归纳总结
等差数列前n项和计算的三种方法
C
练一练
练一练
B
例1 已知数列{an}的前n项和为Sn=-2n2+3n+1.
(1)求数列{an}的通项公式;
(2)数列{an}是否为等差数列?
题型4 an与Sn的关系的应用
典例剖析
归纳总结
已知Sn求an的一般步骤
解析:当n≥2时,an=Sn-Sn-1=n2-9n-(n-1)2+9(n-1)=2n-10,
当n=1时,a1=S1=-8也适合,所以an=2n-10.
又因为5<ak<8,所以5<2k-10<8,解得7.5<k<9,故k=8.
5.已知数列{an}的前n项和Sn=n2-9n,第k项满足5<ak<8,则k=( )
A.9 B.8
C.7 D.6
练一练
B
例2 在等差数列{an}中,设Sn为其前n项和,且a1>0,S3=S11,当Sn取得最大值时,n的值为____.
7
题型5 等差数列前n项和的最值
典例剖析
6.在等差数列{an}中,设Sn为其前n项和, an=26-2n ,当Sn取得最大值时,n的值为____________.
12或13
练一练
7.在等差数列{an}中,设Sn为其前n项和,且a1>0,a2 019+a2 020>0,a2 019·a2 020<0,求使Sn>0成立的最大自然数n
1.在等差数列中,求Sn的最值的2种常用方法
归纳总结
归纳总结
2.寻求正、负项分界点的方法
8.设等差数列{an}的前n项和为Sn,且S2 020>0,S2 021<0,则当n=________时,Sn最大.
1 010
练一练
例3 已知等差数列{an}中,公差d>0,a1+a4+a7=-6,a2·a4·a6=24.
(1)求数列{an}的通项公式;
典例剖析
题型6 求数列{|an|}的前n项和
(2)Sn为数列{|an|}的前n项和,求Sn.
归纳总结
练一练
1.已知数列{an}的通项公式为an=2-3n,n∈N+,则{an}的前n项和Sn等于( )
随堂练
2.若等差数列{an}的前5项和S5=25,且a2=3,则a7等于( )
A.12 B.13 C.14 D.15
A
B
3.在等差数列{an}中,若S10=120,则a1+a10的值是( )
A.12 B.24 C.36 D.48
4.设等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a7+a8+a9等于( )
A.63 B.45 C.36 D.27
随堂练
B
B
5.在各项均为正数的等差数列{an}中,已知公差d=2,an=11,Sn=35,
则a1=____,n=____.
3
5
6.已知数列{an}的前n项和Sn=n2+n,则an=_____.
2n
随堂练
7.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为_____.
3
8.首项为正数的等差数列,前n项和为Sn,且S3=S8,当n=______时,Sn取到最大值.
5或6
随堂练
错因分析
易错辨析 混淆等差数列的性质致误
例4 已知等差数列{an}的前n项之和记为Sn,S10=10,S30=70,则S40=________.
120
【易错警示】
错因分析
出错原因:将等差数列中Sm,S2m-Sm,S3m-S2m
成等差数列误认为Sm,S2m,S3m成等差数列.
纠错心得:
本题可用等差数列的性质:Sm,S2m-Sm,S3m-S2m成等差数列求解;还可以由S10=10,S30=70联立方程组解得a1和d,再求S40.
例5 设等差数列{an}的前n项和为Sn,且满足S11=S18,则当n=________时,Sn最大.
14或15
易错辨析 数列中的最值错误
错因分析
错因分析
【易错警示】
出错原因:由于a15=0,所以S14=S15,即n=14或n=15时,前n项和相等且最大.有些同学容易忽视数列中为零的项致错.
纠错心得:在解决数列问题时,经常遇到求最值的问题,且解决此类问题常用函数的一些方法,但一定要注意数列中的变量n为正整数,同时还要注意数列中为零的项.
错因分析
1.已知数列{an}中,a1=1,an=an-1+ (n≥2,n∈N+),则数列{an}的前9项和等于( )
A.27 B. C.45 D.-9
分层练习-基础
2.(多选)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5
B.an=3n-10
C.Sn=n2-4n
C
A
4.已知一个等差数列共n项,且其前四项之和为21,末四项之和为67,前n项和为286,则项数n为( )
A.24 B.26 C.25 D.28
分层练习-基础
( )
A
B
5.一物体从1 960米的高空降落,如果第1秒降落4.90米,以后每秒比前一秒多降落9.80米,那么经过________秒落到地面
A.18 B.19 C.20 D.21
6.在小于100的自然数中,所有被7除余2的数之和为( )
A.765 B.665
C.763 D.663
分层练习-基础
C
B
7.设等差数列{an}的前n项和为Sn,若a2=-3,S5=-10,则a5=______.
0
8.将数列{2n-1}与{3n-2}的公共项从小到大排列得到数列{an},则{an}的前n项和为________.
3n2-2n
分层练习-基础
9.在等差数列{an}中.
解得n=15.
分层练习-基础
(2)a1=4,S8=172,求a8和d.
解得a8=39,
又∵a8=4+(8-1)d=39,∴d=5.
∴a8=39,d=5.
分层练习-基础
10.已知数列{an}的前n项和为Sn=n2+n-1,求数列{an}的通项公式,并判断它是不是等差数列.
分层练习-基础
当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=(n2+n-1)-[(n-1)2+(n-1)-1]=2n.
又a1=1不满足an=2n,
∵a2-a1=4-1=3≠a3-a2=2,
∴数列{an}中每一项与前一项的差不是同一个常数,
∴数列{an}不是等差数列,数列{an}是从第二项起以2为公差的等差数列.
11.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,则第八个孩子分得斤数为( )
A.65 B.176 C.183 D.184
分层练习-巩固
D
12.在等差数列{an}中,已知a1=-12,S13=0,则使得an>0的最小正整数n为( )
A.7 B.8
C.9 D.10
分层练习-巩固
13.已知正项等差数列{an}的前n项和为Sn,S10=40,则a3a8的最大值为______.
16
B
14.已知{an}为等差数列,Sn为数列{an}的前n项和,且S7=7,S15=75,
则数列 的前n项和Tn=________.
15.(多选)已知Sn是等差数列{an}的前n项和,且S6>S7>S5,则下列说法正确的是( )
A.d<0
B.S11>0
C.S12<0
D.数列{Sn}中的最大项为S11
分层练习-巩固
A B
16.已知公差大于零的等差数列{an}的前n项和为Sn,n∈N+,且满足:a3a4=117,a2+a5=22.
(1)数列{an}的通项公式an=________.
4n-3
分层练习-拓展
(2)若数列{bn}是等差数列,且bn= ,则非零常数c=________.
17.某仓库有同一型号的圆钢600根,堆放成如图所示的形状,从第二层开始,每一层比下面一层少放一根,而第一层至少要比第二层少一根,要使堆垛的占地面积最小(即最下面一层根数最少),则最下面一层放几根?共堆了多少层?
分层练习-拓展
所以n2+n-1 200≥0,记 (n)=n2+n-1 200,
因为当n∈N+时,f(n)单调递增,
而f(35)=60>0,f(34)=-10<0,
所以n≥35,因此最下面一层最少放35根.
分层练习-拓展
因为1+2+3+…+35=630,
所以最多可堆放630根,必须去掉上面30根,去掉顶上7层,共1+2+3+…+7=28(根),再去掉顶上第8层的2根,剩下的600根共堆了28层.
故最下面一层放35根,共堆了28层.
分层练习-拓展
18.已知Sn为等差数列{an}的前n项和,且a1=-15,S5=-55.
(1)求数列{an}的通项公式;
设等差数列{an}的公差为d,
∴a3=-11,
∴an=a1+(n-1)d=-15+(n-1)×2=2n-17,n∈N+.
分层练习-拓展
(2)若不等式Sn>t对于任意的n∈N+恒成立,求实数t的取值范围.
由(1)知,an=2n-17,
∴(Sn)min=-64.
Sn>t对任意的n∈N+恒成立等价于(Sn)min>t,
即-64>t.∴t∈(-∞,-64).
分层练习-拓展
1.知识清单:
(1)等差数列前n项和及其计算公式.
(2)等差数列在实际问题中的应用.
(3)利用等差数列前n项和公式判断等差数列.
(4)等差数列前n项和的最值问题.
(5)等差数列前n项和的性质及应用.
2.方法归纳:函数与方程思想、倒序相加法、整体思想、分类讨论数形结合思想.
3.常见误区
(1)由Sn求通项公式时忽略对n=1的讨论.
(2)求等差数列前n项和的最值时,忽视条件n∈N+导致错误.
(3)不注意运用性质导致解题烦琐.
课堂小结
湘教版2019高一数学(选修一) 第一章 数列
1.2.3 等差数列的前n项和
1.2 等差数列
学习目标
1.掌握等差数列前n项和公式及其获取思路.
2.熟练掌握等差数列的五个量a1,d,n,an,Sn的关系,能够由其中任意三个求另外两个.
3.能用an与Sn的关系求an.
4.会利用等差数列前n项和的性质简化求和运算.
5.会利用等差数列前n项和的函数特征求最值.
情景导入
高斯(1777-1855),德国著名数学家、物理学家、天文学家,是近代数学的奠基人之一,享有“数学王子”的美誉.高斯7岁时,有一天老师在黑板上出一道题“1+2+3+4+5+…+100=?”对全班同学说:“你们算一算从1开始一直加到100的和是多少?”,同学们不约而同地拿出笔在小石板上沙沙地算起来.不到一分钟,高斯站起来说:“老师,我算出结果来了,是5 050!”老师和其他同学都很吃惊.你知道高斯是怎样快速计算出来的吗?
1.等差数列的前 n 项和
新知探究
被世人誉为"数学王子"的德国数学家高斯在幼年就显示出过人的数学天赋,他的老师布置了一道看上去很难的题,计算1+2+3+...+100=?高斯经过细致的观察,迅捷地报出了得数:5 050.
在老师与同学露出惊讶之色时,他解释了自己的思考过程:
将这 100个数分成 50 个数对,其中1+100=101,2+99=101,…, 50+51=101,于是 100 个数的和就是 50 个101,即 50× 101=5 050.
高斯的算法实际上解决了求等差数列1,2,3,…,n, …前100项之和的问题.
事实上,古代的中国人和希腊人也是这么求等差数列之和的.例如:我国南宋数学家杨辉提出了这样一个问题:“今有圭垛草一堆,顶上一束,底阔八束.问共几束?答:36束.”
8层
{
{
9束
他的计算方法可以用右图来表示.
设想有另外一堆同样的草,将其倒置,并和原来的草堆拼在一起,这就得到 8×9 的草堆,一共 72 束,因此原来的草堆共有 36 束.
在特殊问题中高斯运用的是“两两配对”的方法,那对于一般等差数列的求和问题,也能否这样处理呢?这个就不行了,因为n不一定是偶数,这样就不好“两两配对”了,这时我们就要改进方法了.
前人计算等差数列前n项和的方法的确巧妙,那么这种方法能推广到求一般等差数列的前n项和吗?
设等差数列{an}的前n项和为Sn,公差为d,即
Sn=a1+a2+a3+…… + an
再将项的次序反过来,Sn可以写成
Sn=an+an-1+an-2+…… +a1
两式两边分别相加,得
2Sn= (a1+an)+(a2+an-1)+(a3+an-2)+…… +(an +a1)
= n (a1+an)
由此得到等差数列{an}的前n项和的公式
又因为an=a1+(n-1)d,
所以上述公式又可以写成
如果数列{an}为等差数列,那么
an+ am = ap+ aq
(n,m,p,q∈N+)
(a1+an)=(a2+an-1)=(a2+an-1)=…
这个公式表明,等差数列的前n项和可由首项、公差和项数唯一确定.
等差数列的通项公式和前n项和公式中,共有“a1,d ,n,an,Sn”五个
量,故知三可求其二.
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
概念归纳
例 7 某体育馆一角的看台上有20排,每一排比前一排多两个座位,若第一排有15个座位,则体育馆一角里共有多少个座位?
解: 设第n排的座位有an个,
则得到的数列{an}(1≤n≤20)是首项为15,公差为2的等差数列.
根据等差数列前n项和公式,
这一角里总共的座位数为
课本例题
课本例题
例 8 已知一个等差数列的前10项和是310,前 20项和是1220,求该数列的前n项和.
解: 记该数列为{an},公差为d,
根据等差数列前n项和公式,可得
S10=10a1+45d =310,S20=20a1+190d =1220,
解得a1=4,d =6,
因此该等差数列的前n项和为
解: 因为Sn=n2+2n,
所以当n ≥2 时,有
an=Sn-Sn-1
=(n2+2n)-[(n-1)2+2(n-1)]
=2n+1,
又当n=1时,a1=S1=12+2=3,符合上式,
所以数列{an}的通项公式an=2n+1.
当n ≥2 时,有an-an-1=(2n+1)-[2(n-1)+1]=2,
所以数列{an}是以3为首项,以2为公差的等差数列.
设等差数列{an}的前n项和为Sn,
则
所以等差数列的前n项和公式Sn可以看成关于n的二次函数(常数项为0).
例 9 设数列{an}的前n项和Sn=n2+2n,求证:{an}是等差数列.
课本例题
例10 已知Sn为等差数列{an}的前n项和,且a1=25,S17=S9.
(1)求数列{an}的通项公式;
(2)求 Sn的最大值及对应的n值.
解: (1)记数列{an}的公差为d,由S17=S9,可得
17a1+136d =9a1+36d ,
又a1=25,解得d =-2,
所以an=25+(n-1)ⅹ(-2)=27-2n.
课本例题
例10 已知Sn为等差数列{an}的前n项和,且a1=25,S17=S9.
(1)求数列{an}的通项公式; an=27-2n
(2)求Sn的最大值及对应的n值.
解: (2)因为
所以当n=13 时,Sn取最大值,S13=169.
解: (2)令an=27-2n>0,得n<13.5
即当n≤13时,an>0,当n≥14时,an<0,
故当n=13 时,Sn取最大值,S13=13ⅹ25+78ⅹ(-2)=169.
课本例题
已知等差数列{an}的前n项和为Sn.
(1)求证:S2,S4-S2,S6-S4成等差数列;
(2)求证:S3,S6-S3,S9-S6 成等差数列;
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
证明:记数列{an}的公差为d,
因为S2 = a1+a2,S4-S2 = a3+a4,S6-S4 = a5+a6,
所以(S4-S2)-S2 = (a3+a4)-(a1+a2) = 4d,
(S6-S4)-(S4-S2) = (a5+a6)-(a3+a4) = 4d,
即 (S6-S4)-(S4-S2) = (S4-S2)-S2,
所以S2,S4-S2,S6-S4成等差数列.
思考探究
已知等差数列{an}的前n项和为Sn.
(1)求证:S2,S4-S2,S6-S4成等差数列;
(2)求证:S3,S6-S3,S9-S6 成等差数列;
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
证明:记数列{an}的公差为d,
因为S3 = a1+a2+a3,S6-S3 = a4+a5+a6,S9-S6 = a7+a8+a9,
所以(S6-S3)-S3 = (a4+a5+a6)-(a1+a2+a3) = 9d,
(S9-S6 )-(S6-S3) = (a7+a8+a9)-(a4+a5+a6) = 9d,
即 (S9-S6 )-(S6-S3) = (S6-S3)-S3,
所以S3,S6-S3,S9-S6成等差数列.
思考探究
已知等差数列{an}的前n项和为Sn,.
(3)试推广(1)和(2)的结果,写出你的结论并加以证明.
猜想:Sm,S2m-Sm,S3m-S2m成等差数列.
证明:因为Sm = a1+a2+……+am,
S2m-Sm = am+1+ am+2+……+a2m,
S3m-S2m = a2m+1+ a2m+2+……+a3m,
所以(S2m-Sm)-Sm =m2d,
(S3m-S2m)-(S2m-Sm)==m2d,
即 (S3m-S2m)-(S2m-Sm) = (S2m-Sm)-Sm,
所以Sm,S2m-Sm,S3m-S2m成等差数列.
思考探究
1.若在等差数列{an}中,有a1+a4+a7=10,a3+a6+a9=22,
则a2+a5+a8= .
解:记数列{an}的公差为d,
因为(a3+a6+a9)-(a1+a4+a7)
=(a3-a1)+ (a6-a4)+(a9-a7)
=6d =12,
所以 d =2,
所以a2+a5+a8=(a1+d)+(a4+d)+(a7+d)=(a1+a4+a7)+3d =16.
练一练
概念归纳
等差数列的前项和n公式:
如果等差数列{an}的首项a1,公差为d ,那么该等差数列的前n项和公式为:
等差数列的前n项和公式Sn可以看成关于n的二次函数(常数项为0).
若等差数列的前n项和为Sn,则Sm,S2m-Sm,S3m-S2m成等差数列.
题型1 等差数列前n项和的基本计算
典例剖析
(2)已知a1=4,S8=172,求a8和d;
(3)已知d=2,an=11,Sn=35,求a1和n.
等差数列中基本计算的两个技巧
(1)利用基本量求值
(2)利用等差数列的性质解题
归纳总结
练一练
C
-4
练一练
解析:由题意知,该地区9月份前10天流感病毒的新感染者人数,
构成一个首项a1=40,公差d=40的等差数列,
所以9月10日的新感染者人数为a10=40+(10-1)×40=400(人),
所以9月11日的新感染者人数为a11=400-10=390(人);
例2 某地去年9月份曾发生流感,据统计,9月1日该地区流感病毒的新感染者有40人,此后,每天的新感染者人数比前一天新感染者人数增加40.从9月11日起,该地区医疗部门采取措施,使该种病毒的传播得到有效控制,每天的新感染者人数比前一天的新感染者人数减少10.
(1)分别求出该地区在9月10日和9月11日这两天的流感病毒的新感染者人数;
题型2 等差数列前n项和公式的实际应用
典例剖析
(2)该地区9月份(共30天)流感病毒的新感染者共有多少人?
归纳总结
(1)解答与等差数列前n项和有关的应用题,其关键在于构造合适的等差数列.
(2)遇到与正整数有关的应用题时,可以考虑与数列知识联系,建立数列模型,具体解决要注意以下两点:
①抓住实际问题的特征,明确是什么类型的数列模型.
②深入分析题意,确定是求通项公式an,或是求前n项和Sn,还是求项数n.
3.[2022·湖南部分重点中学联考]跑步是一项有氧运动,通过跑步,我们能提高肌力,同时提高体内的基础代谢水平,加速脂肪的燃烧,养成易瘦体质.小林最近给自己制定了一个200千米的跑步健身计划,他第一天跑了8千米,以后每天比前一天多跑0.5千米,则他要完成该计划至少需要( )
A.16天 B.17天 C.18天 D.19天
练一练
B
解析:由等差数列{an}的性质,
.可得Sm,S2m-Sm,S3m-S2m成等差数列,
即30,70,S3m-100成等差数列,
所以2×70=30+S3m-100,解得S3m=210.
例3 (1)等差数列{an}的前m项和为30,前2m项和为100,求数列{an}的前3m项的和S3m;
题型3 等差数列前n项和性质的应用
典例剖析
归纳总结
等差数列前n项和计算的三种方法
C
练一练
练一练
B
例1 已知数列{an}的前n项和为Sn=-2n2+3n+1.
(1)求数列{an}的通项公式;
(2)数列{an}是否为等差数列?
题型4 an与Sn的关系的应用
典例剖析
归纳总结
已知Sn求an的一般步骤
解析:当n≥2时,an=Sn-Sn-1=n2-9n-(n-1)2+9(n-1)=2n-10,
当n=1时,a1=S1=-8也适合,所以an=2n-10.
又因为5<ak<8,所以5<2k-10<8,解得7.5<k<9,故k=8.
5.已知数列{an}的前n项和Sn=n2-9n,第k项满足5<ak<8,则k=( )
A.9 B.8
C.7 D.6
练一练
B
例2 在等差数列{an}中,设Sn为其前n项和,且a1>0,S3=S11,当Sn取得最大值时,n的值为____.
7
题型5 等差数列前n项和的最值
典例剖析
6.在等差数列{an}中,设Sn为其前n项和, an=26-2n ,当Sn取得最大值时,n的值为____________.
12或13
练一练
7.在等差数列{an}中,设Sn为其前n项和,且a1>0,a2 019+a2 020>0,a2 019·a2 020<0,求使Sn>0成立的最大自然数n
1.在等差数列中,求Sn的最值的2种常用方法
归纳总结
归纳总结
2.寻求正、负项分界点的方法
8.设等差数列{an}的前n项和为Sn,且S2 020>0,S2 021<0,则当n=________时,Sn最大.
1 010
练一练
例3 已知等差数列{an}中,公差d>0,a1+a4+a7=-6,a2·a4·a6=24.
(1)求数列{an}的通项公式;
典例剖析
题型6 求数列{|an|}的前n项和
(2)Sn为数列{|an|}的前n项和,求Sn.
归纳总结
练一练
1.已知数列{an}的通项公式为an=2-3n,n∈N+,则{an}的前n项和Sn等于( )
随堂练
2.若等差数列{an}的前5项和S5=25,且a2=3,则a7等于( )
A.12 B.13 C.14 D.15
A
B
3.在等差数列{an}中,若S10=120,则a1+a10的值是( )
A.12 B.24 C.36 D.48
4.设等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a7+a8+a9等于( )
A.63 B.45 C.36 D.27
随堂练
B
B
5.在各项均为正数的等差数列{an}中,已知公差d=2,an=11,Sn=35,
则a1=____,n=____.
3
5
6.已知数列{an}的前n项和Sn=n2+n,则an=_____.
2n
随堂练
7.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为_____.
3
8.首项为正数的等差数列,前n项和为Sn,且S3=S8,当n=______时,Sn取到最大值.
5或6
随堂练
错因分析
易错辨析 混淆等差数列的性质致误
例4 已知等差数列{an}的前n项之和记为Sn,S10=10,S30=70,则S40=________.
120
【易错警示】
错因分析
出错原因:将等差数列中Sm,S2m-Sm,S3m-S2m
成等差数列误认为Sm,S2m,S3m成等差数列.
纠错心得:
本题可用等差数列的性质:Sm,S2m-Sm,S3m-S2m成等差数列求解;还可以由S10=10,S30=70联立方程组解得a1和d,再求S40.
例5 设等差数列{an}的前n项和为Sn,且满足S11=S18,则当n=________时,Sn最大.
14或15
易错辨析 数列中的最值错误
错因分析
错因分析
【易错警示】
出错原因:由于a15=0,所以S14=S15,即n=14或n=15时,前n项和相等且最大.有些同学容易忽视数列中为零的项致错.
纠错心得:在解决数列问题时,经常遇到求最值的问题,且解决此类问题常用函数的一些方法,但一定要注意数列中的变量n为正整数,同时还要注意数列中为零的项.
错因分析
1.已知数列{an}中,a1=1,an=an-1+ (n≥2,n∈N+),则数列{an}的前9项和等于( )
A.27 B. C.45 D.-9
分层练习-基础
2.(多选)记Sn为等差数列{an}的前n项和.已知S4=0,a5=5,则( )
A.an=2n-5
B.an=3n-10
C.Sn=n2-4n
C
A
4.已知一个等差数列共n项,且其前四项之和为21,末四项之和为67,前n项和为286,则项数n为( )
A.24 B.26 C.25 D.28
分层练习-基础
( )
A
B
5.一物体从1 960米的高空降落,如果第1秒降落4.90米,以后每秒比前一秒多降落9.80米,那么经过________秒落到地面
A.18 B.19 C.20 D.21
6.在小于100的自然数中,所有被7除余2的数之和为( )
A.765 B.665
C.763 D.663
分层练习-基础
C
B
7.设等差数列{an}的前n项和为Sn,若a2=-3,S5=-10,则a5=______.
0
8.将数列{2n-1}与{3n-2}的公共项从小到大排列得到数列{an},则{an}的前n项和为________.
3n2-2n
分层练习-基础
9.在等差数列{an}中.
解得n=15.
分层练习-基础
(2)a1=4,S8=172,求a8和d.
解得a8=39,
又∵a8=4+(8-1)d=39,∴d=5.
∴a8=39,d=5.
分层练习-基础
10.已知数列{an}的前n项和为Sn=n2+n-1,求数列{an}的通项公式,并判断它是不是等差数列.
分层练习-基础
当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=(n2+n-1)-[(n-1)2+(n-1)-1]=2n.
又a1=1不满足an=2n,
∵a2-a1=4-1=3≠a3-a2=2,
∴数列{an}中每一项与前一项的差不是同一个常数,
∴数列{an}不是等差数列,数列{an}是从第二项起以2为公差的等差数列.
11.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,则第八个孩子分得斤数为( )
A.65 B.176 C.183 D.184
分层练习-巩固
D
12.在等差数列{an}中,已知a1=-12,S13=0,则使得an>0的最小正整数n为( )
A.7 B.8
C.9 D.10
分层练习-巩固
13.已知正项等差数列{an}的前n项和为Sn,S10=40,则a3a8的最大值为______.
16
B
14.已知{an}为等差数列,Sn为数列{an}的前n项和,且S7=7,S15=75,
则数列 的前n项和Tn=________.
15.(多选)已知Sn是等差数列{an}的前n项和,且S6>S7>S5,则下列说法正确的是( )
A.d<0
B.S11>0
C.S12<0
D.数列{Sn}中的最大项为S11
分层练习-巩固
A B
16.已知公差大于零的等差数列{an}的前n项和为Sn,n∈N+,且满足:a3a4=117,a2+a5=22.
(1)数列{an}的通项公式an=________.
4n-3
分层练习-拓展
(2)若数列{bn}是等差数列,且bn= ,则非零常数c=________.
17.某仓库有同一型号的圆钢600根,堆放成如图所示的形状,从第二层开始,每一层比下面一层少放一根,而第一层至少要比第二层少一根,要使堆垛的占地面积最小(即最下面一层根数最少),则最下面一层放几根?共堆了多少层?
分层练习-拓展
所以n2+n-1 200≥0,记 (n)=n2+n-1 200,
因为当n∈N+时,f(n)单调递增,
而f(35)=60>0,f(34)=-10<0,
所以n≥35,因此最下面一层最少放35根.
分层练习-拓展
因为1+2+3+…+35=630,
所以最多可堆放630根,必须去掉上面30根,去掉顶上7层,共1+2+3+…+7=28(根),再去掉顶上第8层的2根,剩下的600根共堆了28层.
故最下面一层放35根,共堆了28层.
分层练习-拓展
18.已知Sn为等差数列{an}的前n项和,且a1=-15,S5=-55.
(1)求数列{an}的通项公式;
设等差数列{an}的公差为d,
∴a3=-11,
∴an=a1+(n-1)d=-15+(n-1)×2=2n-17,n∈N+.
分层练习-拓展
(2)若不等式Sn>t对于任意的n∈N+恒成立,求实数t的取值范围.
由(1)知,an=2n-17,
∴(Sn)min=-64.
Sn>t对任意的n∈N+恒成立等价于(Sn)min>t,
即-64>t.∴t∈(-∞,-64).
分层练习-拓展
1.知识清单:
(1)等差数列前n项和及其计算公式.
(2)等差数列在实际问题中的应用.
(3)利用等差数列前n项和公式判断等差数列.
(4)等差数列前n项和的最值问题.
(5)等差数列前n项和的性质及应用.
2.方法归纳:函数与方程思想、倒序相加法、整体思想、分类讨论数形结合思想.
3.常见误区
(1)由Sn求通项公式时忽略对n=1的讨论.
(2)求等差数列前n项和的最值时,忽视条件n∈N+导致错误.
(3)不注意运用性质导致解题烦琐.
课堂小结
同课章节目录
