湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.3直线的一般式方程课件(共36张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.3直线的一般式方程课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:42:28 | ||
图片预览










文档简介
(共36张PPT)
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2 直线的方程
2.2.3 直线的一般式方程
学习目标
1.直线的一般式方程(重点)
2.理解二元一次方程能表示所有直线(重点、难点)
3.掌握各直线方程形式之间的转化(重点)
直线的方程
名称 已知条件 方程 适用范围
点斜式 过点 P0(x0, y0),斜率为 k
斜截式 纵截距为 b,
斜率为 k
两点式 过点P1(x1,y1),P2(x2,y2)
截距式 横截距和纵截距分别为 a 和 b
y -y0 = k (x-x0)
y = k x + b
(y2-y1)(x-x1)-(x2-x1)(y-y1)=0
不表示垂直x轴的直线
即斜率不存在的直线
所有直线
不表示垂直于坐标轴和经过原点的直线
不表示垂直x轴的直线
即斜率不存在的直线
复习导入
情景导入
前面我们学习了直线的点斜式、斜截式、两点式、截距式方程,可以发现它们都是二元一次方程.现在请同学们思考一下,在平面直角坐标系中的每一条直线是否都可以用一个关于x,y的二元一次方程表示呢?
问题1 平面直角坐标系中的任何一条直线的方程都是关于x,y的二元一次方程吗?
新知探究
直线的一般式方程
当直线与x轴不垂直时,直线的斜率存在,于是经过点P1(x1,y1),斜率为k的直线的方程为y-y1=k(x-x1),即kx-y+y1-kx1=0,此方程是关于x,y的二元一次方程.
当直线与x轴垂直时,直线的斜率不存在,于是经过点P1(x1,y1)的直线的方程为x=x1,即x+0·y-x1=0,此方程也可看作是关于x,y的二元一次方程.
因此,平面直角坐标系中的任意一条直线都可以用关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)来表示.
问题2 每一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示平面直角坐标系中的一条直线吗?
因此,在平面直角坐标系中,关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示一条直线.
平面直角坐标系中任意一条直线都可以用关于x,y的二元一次方程 Ax十By+C=0(A,B不同时为0)来表示.
关于x,y的二元一次方程都表示一条直线.
我们把方程
Ax十By+C=0(A,B不同时为0)
称为直线的一般式方程,简称一般式.
概念归纳
例6已知直线 l 的方程为3x十4y-12=0.
(1)求直线 l 的斜率;
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解: (1)将直线 l 的一般式方程化为斜截式,得到
因此直线 l 的斜率为 .
课本例题
例6 已知直线 l 的方程为3x十4y-12=0.
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解:方法一:(2)如图,设直线 l 交x轴于点A(a,0),
交y轴于点B(0,b).
对于直线方程3x十4y-12=0,令y=0,得x=4;
令x =0,得y=3.
于是得a=4,b=3 .
因此
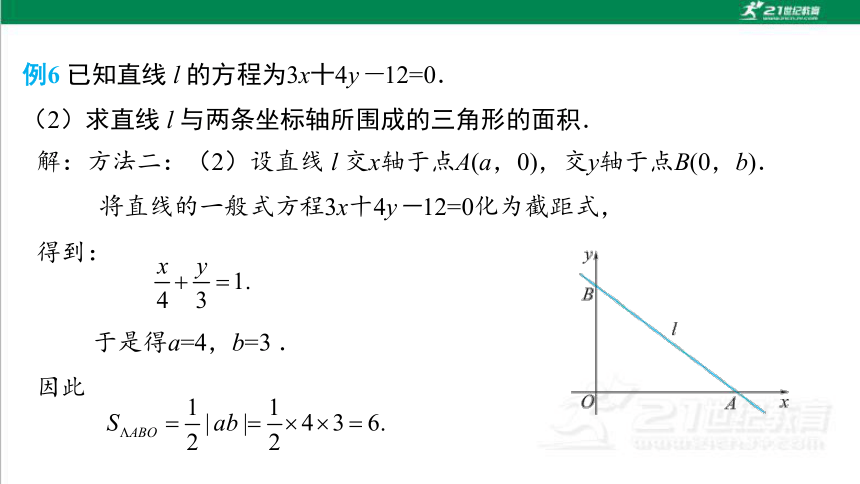
例6 已知直线 l 的方程为3x十4y-12=0.
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解:方法二:(2)设直线 l 交x轴于点A(a,0),交y轴于点B(0,b).
将直线的一般式方程3x十4y-12=0化为截距式,
得到:
于是得a=4,b=3 .
因此
课堂练习:课本第67页
典例剖析
求直线的一般式方程的策略
归纳总结
【变式练】(1)过点P(-2,3),并且在两坐标轴上的截距互为相反数的直线方程是( )
A.x-y+1=0 B.x-y+1=0或3x+2y=0
C.x-y-5=0 D.x-y+5=0或3x+2y=0
D
2x+y+3=0
题型2 用直线的一般式方程解决直线与坐标轴形成三角形问题
例2 设直线l的方程为(a+1)x+y-2-a=0(a∈R),若a>-1,直线l与x,y轴分别交于M,N两点,O为坐标原点,求△OMN面积取最小值时,直线l的方程.
典例剖析
归纳总结
由直线的一般式方程表示直线与坐标轴形成三角形的面积的步骤
题型3 由含参数的一般式方程求参数(或取值范围)
例3 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
典例剖析
(2)为使直线l不经过第二象限,求a的取值范围.
变式探究1 本例中若直线不经过第四象限,则a的取值范围是什么?
解析:由本例(2)解法可知直线OA的斜率为3,要使直线不经过第四象限,则有a≤3.
变式探究2 本例中将方程改为“x-(a-1)y-a-2=0”,若直线不经过第二象限,则a的取值范围又是什么?
归纳总结
求直线过定点的2种方法
【变式练】已知(k+1)x-(k-1)y-2k=0为直线l的方程,求证:不论k取何实数,直线l必过定点,并求出这个定点的坐标.
已知直线l1:mx+8y+m-10=0和直线l2:x+2my-4=0垂直,则m=________.
0
错因分析
易错分析:忽视斜率不存在
错因分析
注意:含参数的直线方程中,一定注意垂直于x轴的情况,
此情况直线方程存在而斜率不存在,常常忽视而漏解.
易错分析:忽视斜率不存在,把直线的一般式化为斜截式得
,导致出错.
错因分析
分析:讨论截距是否0,分别求出直线即可.
错因分析
√
√
√
×
分层练习-基础
D
3.直线x-y-1=0的倾斜角α为( )
A.30° B.45° C.60° D.90°
B
解析:根据题意,易知直线x-y-1=0的斜率k=1,由tan α=k=1,得α=45°.
4.若方程Ax+By+C=0表示直线,则A,B应满足的条件为( )
A.A≠0 B.B≠0 C.A·B≠0 D.A2+B2≠0
解析:根据直线方程的一般式可知,要使得Ax+By+C=0表示直线,则A,B不能同时为零,即A2+B2≠0.
D
5.斜率为2,且经过点A(1,3)的直线的一般式方程为____________.
解析:由直线点斜式方程可得y-3=2(x-1),化为一般式为:2x-y+1=0.
2x-y+1=0
6.直线x+(a2+1)y+1=0的倾斜角的取值范围是( )
D
分层练习-巩固
7.已知两条直线a1x+b1y+4=0和a2x+b2y+4=0都过点A(2,3),则过两点P1(a1,b1),P2(a2,b2)的直线方程为_____________.
2x+3y+4=0
∵两条直线a1x+b1y+4=0和a2x+b2y+4=0都过点A(2,3),
∴2a1+3b1+4=0,2a2+3b2+4=0,
因此过两点P1(a1,b1),P2(a2,b2)的直线的方程为2x+3y+4=0.
8.若点A(-2,-1)在直线mx+ny+1=0上,其中m,n均大于0,则
的最小值为____.
8
分层练习-拓展
9.直线l过原点,且垂直于向量(1,-3).若角α的终边落在直线l上,则
=_______.
因为直线l过原点,且垂直于向量(1,-3),所以直线l的方程为x-3y=0,
10.已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
直线l的方程可化为y-1=k(x+2),由点斜式方程可知,直线l过定点(-2,1).
(2)若直线l不经过第四象限,求k的取值范围;
解得k>0;
当k=0时,直线l的方程为y=1,符合题意,
故k的取值范围是[0,+∞).
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,△AOB的面积为S(O为坐标原点),求S的最小值并求此时直线l的方程.
由题意可知k≠0,再由l的方程,
∴Smin=4,此时直线l的方程为x-2y+4=0.
解得k>0.
课堂小结
直线的方程
× √ √
× √ √
× × √
× × ×
√ √ √
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2 直线的方程
2.2.3 直线的一般式方程
学习目标
1.直线的一般式方程(重点)
2.理解二元一次方程能表示所有直线(重点、难点)
3.掌握各直线方程形式之间的转化(重点)
直线的方程
名称 已知条件 方程 适用范围
点斜式 过点 P0(x0, y0),斜率为 k
斜截式 纵截距为 b,
斜率为 k
两点式 过点P1(x1,y1),P2(x2,y2)
截距式 横截距和纵截距分别为 a 和 b
y -y0 = k (x-x0)
y = k x + b
(y2-y1)(x-x1)-(x2-x1)(y-y1)=0
不表示垂直x轴的直线
即斜率不存在的直线
所有直线
不表示垂直于坐标轴和经过原点的直线
不表示垂直x轴的直线
即斜率不存在的直线
复习导入
情景导入
前面我们学习了直线的点斜式、斜截式、两点式、截距式方程,可以发现它们都是二元一次方程.现在请同学们思考一下,在平面直角坐标系中的每一条直线是否都可以用一个关于x,y的二元一次方程表示呢?
问题1 平面直角坐标系中的任何一条直线的方程都是关于x,y的二元一次方程吗?
新知探究
直线的一般式方程
当直线与x轴不垂直时,直线的斜率存在,于是经过点P1(x1,y1),斜率为k的直线的方程为y-y1=k(x-x1),即kx-y+y1-kx1=0,此方程是关于x,y的二元一次方程.
当直线与x轴垂直时,直线的斜率不存在,于是经过点P1(x1,y1)的直线的方程为x=x1,即x+0·y-x1=0,此方程也可看作是关于x,y的二元一次方程.
因此,平面直角坐标系中的任意一条直线都可以用关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)来表示.
问题2 每一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示平面直角坐标系中的一条直线吗?
因此,在平面直角坐标系中,关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示一条直线.
平面直角坐标系中任意一条直线都可以用关于x,y的二元一次方程 Ax十By+C=0(A,B不同时为0)来表示.
关于x,y的二元一次方程都表示一条直线.
我们把方程
Ax十By+C=0(A,B不同时为0)
称为直线的一般式方程,简称一般式.
概念归纳
例6已知直线 l 的方程为3x十4y-12=0.
(1)求直线 l 的斜率;
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解: (1)将直线 l 的一般式方程化为斜截式,得到
因此直线 l 的斜率为 .
课本例题
例6 已知直线 l 的方程为3x十4y-12=0.
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解:方法一:(2)如图,设直线 l 交x轴于点A(a,0),
交y轴于点B(0,b).
对于直线方程3x十4y-12=0,令y=0,得x=4;
令x =0,得y=3.
于是得a=4,b=3 .
因此
例6 已知直线 l 的方程为3x十4y-12=0.
(2)求直线 l 与两条坐标轴所围成的三角形的面积.
解:方法二:(2)设直线 l 交x轴于点A(a,0),交y轴于点B(0,b).
将直线的一般式方程3x十4y-12=0化为截距式,
得到:
于是得a=4,b=3 .
因此
课堂练习:课本第67页
典例剖析
求直线的一般式方程的策略
归纳总结
【变式练】(1)过点P(-2,3),并且在两坐标轴上的截距互为相反数的直线方程是( )
A.x-y+1=0 B.x-y+1=0或3x+2y=0
C.x-y-5=0 D.x-y+5=0或3x+2y=0
D
2x+y+3=0
题型2 用直线的一般式方程解决直线与坐标轴形成三角形问题
例2 设直线l的方程为(a+1)x+y-2-a=0(a∈R),若a>-1,直线l与x,y轴分别交于M,N两点,O为坐标原点,求△OMN面积取最小值时,直线l的方程.
典例剖析
归纳总结
由直线的一般式方程表示直线与坐标轴形成三角形的面积的步骤
题型3 由含参数的一般式方程求参数(或取值范围)
例3 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
典例剖析
(2)为使直线l不经过第二象限,求a的取值范围.
变式探究1 本例中若直线不经过第四象限,则a的取值范围是什么?
解析:由本例(2)解法可知直线OA的斜率为3,要使直线不经过第四象限,则有a≤3.
变式探究2 本例中将方程改为“x-(a-1)y-a-2=0”,若直线不经过第二象限,则a的取值范围又是什么?
归纳总结
求直线过定点的2种方法
【变式练】已知(k+1)x-(k-1)y-2k=0为直线l的方程,求证:不论k取何实数,直线l必过定点,并求出这个定点的坐标.
已知直线l1:mx+8y+m-10=0和直线l2:x+2my-4=0垂直,则m=________.
0
错因分析
易错分析:忽视斜率不存在
错因分析
注意:含参数的直线方程中,一定注意垂直于x轴的情况,
此情况直线方程存在而斜率不存在,常常忽视而漏解.
易错分析:忽视斜率不存在,把直线的一般式化为斜截式得
,导致出错.
错因分析
分析:讨论截距是否0,分别求出直线即可.
错因分析
√
√
√
×
分层练习-基础
D
3.直线x-y-1=0的倾斜角α为( )
A.30° B.45° C.60° D.90°
B
解析:根据题意,易知直线x-y-1=0的斜率k=1,由tan α=k=1,得α=45°.
4.若方程Ax+By+C=0表示直线,则A,B应满足的条件为( )
A.A≠0 B.B≠0 C.A·B≠0 D.A2+B2≠0
解析:根据直线方程的一般式可知,要使得Ax+By+C=0表示直线,则A,B不能同时为零,即A2+B2≠0.
D
5.斜率为2,且经过点A(1,3)的直线的一般式方程为____________.
解析:由直线点斜式方程可得y-3=2(x-1),化为一般式为:2x-y+1=0.
2x-y+1=0
6.直线x+(a2+1)y+1=0的倾斜角的取值范围是( )
D
分层练习-巩固
7.已知两条直线a1x+b1y+4=0和a2x+b2y+4=0都过点A(2,3),则过两点P1(a1,b1),P2(a2,b2)的直线方程为_____________.
2x+3y+4=0
∵两条直线a1x+b1y+4=0和a2x+b2y+4=0都过点A(2,3),
∴2a1+3b1+4=0,2a2+3b2+4=0,
因此过两点P1(a1,b1),P2(a2,b2)的直线的方程为2x+3y+4=0.
8.若点A(-2,-1)在直线mx+ny+1=0上,其中m,n均大于0,则
的最小值为____.
8
分层练习-拓展
9.直线l过原点,且垂直于向量(1,-3).若角α的终边落在直线l上,则
=_______.
因为直线l过原点,且垂直于向量(1,-3),所以直线l的方程为x-3y=0,
10.已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
直线l的方程可化为y-1=k(x+2),由点斜式方程可知,直线l过定点(-2,1).
(2)若直线l不经过第四象限,求k的取值范围;
解得k>0;
当k=0时,直线l的方程为y=1,符合题意,
故k的取值范围是[0,+∞).
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,△AOB的面积为S(O为坐标原点),求S的最小值并求此时直线l的方程.
由题意可知k≠0,再由l的方程,
∴Smin=4,此时直线l的方程为x-2y+4=0.
解得k>0.
课堂小结
直线的方程
× √ √
× √ √
× × √
× × ×
√ √ √
同课章节目录
