湘教版高中数学选择性必修第一册第1章数列1.4数学归纳法课件(共56张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第1章数列1.4数学归纳法课件(共56张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:42:44 | ||
图片预览











文档简介
(共56张PPT)
湘教版2019高一数学(选修一) 第一章 数列
*1.4 数学归纳法
学习目标
1.了解数学归纳法的原理
2.利用数学归纳法证明等式
3.归纳—猜想—证明
情景导入
如果从盒子里拿出5个小球,发现全部都是绿色的,
是否判断盒子里面的小球都是绿色的?
不能.通过考察部分对象,得到一般的结论的方法,叫不完全归纳法.
不完全归纳法得到的结论不一定正确.
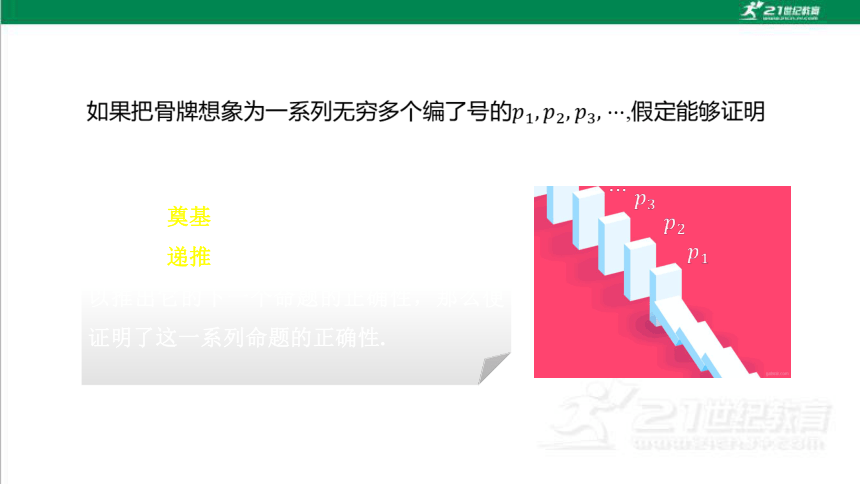
在多米诺骨牌游戏中,我们该如何保证所有的骨牌全部倒下?
要确保任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块滑牌也倒下,这样的话,只需要第一块骨牌倒下,就可导致后面所有的骨牌都能倒下.
情景导入
1.数学归纳法的概念
新知探究
本章研究了大量与正整数 n 有关的数列问题.
请你尝试解决下列问题:
通过对n=1,2,3,4进行归纳,可以猜想数列的通项公式是:
像这样由特殊到一般的推理方法,叫作归纳法.
用归纳法可以帮助我们从一些具体事例中发现一般规律.
当然,仅根据有限的特殊事例归纳得出的结论有时是不正确的.
例如“n +n+11是质数”这个命题对于n=1,2,3,…,9都成立,但当n=10时,10 +10+11=121=11 ,是一个合数.
概念归纳
大家熟悉的“多米诺骨牌效应”或许能给我们以启发.
将骨牌竖立起来摆成一排,并确保任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块骨牌也倒下.若推倒第一块骨牌,它会带倒第二块,再带倒第三块,以此类推,直到所有骨牌全部倒下.
如何找到这样一种推理方法呢?
(1)(奠基)最初的一个命题正确,
(2)(递推)由每一个命题的正确性都可以推出它的下一个命题的正确性,那么便证明了这一系列命题的正确性.
第一步奠基,
证明最初一个命题正确,相当于我们已经亲手“推倒第一块骨牌”.
第二步递推,
意味着“每一块倒下的骨牌怎样将下一块骨牌带倒”.
这样一来,无论有多少块骨牌,只要保证(1)和(2)成立,那么所有的骨牌一定都会倒下.
概念归纳
注意点:
初始值n0选择不一定是1,要结合题意恰当的选择.
(1)用数学归纳法证明:1+2+…+(2n+1)=(n+1)(2n+1),在验证n=1成立时,左边所得的代数式是( )
A.1 B.1+3
C.1+2+3 D.1+2+3+4
当n=1时,2n+1=2×1+1=3,所以左边为1+2+3.
典例剖析
C
(2)用数学归纳法证明1+2+3+…+n2= ,则当n=k+1时,等式左边应在n=k的基础上加上___________________________.
当n=k时,等式左边=1+2+3+…+k2,
当n=k+1时,
等式左边=1+2+3+…+k2+(k2+1)+(k2+2)+…+(k+1)2,
所以在n=k时的左边应加上(k2+1)+(k2+2)+…+(k+1)2.
(k2+1)+(k2+2)+…+(k+1)2
数学归纳法的三个关键点
(1)验证是基础:找准起点,奠基要稳,有些问题中验证的初始值不一定是1.
(2)递推是关键:数学归纳法的实质在于递推,要正确分析式子中项数的变化,弄清式子两边的构成规律.
(3)利用假设是核心:在第二步证明n=k+1时,一定要利用归纳假设.
练一练
所以当n=k+1时,不等式成立,则上述证法( )
A.过程全部正确
B.n=1验证不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
D
2.利用数学归纳法证明等式
新知探究
课本例题
例 2 用数学归纳法证明:
这表明,当n=k+1时,等式也成立.
课本例题
典例剖析
题型 1 用数学归纳法证明等式问题
概念归纳
用数学归纳法证明等式的策略
应用数学归纳法证明等式时需要确定两个式子的结构,即:
(1)n=n0时,等式的结构.
(2)n=k到n=k+1时,两个式子的结构:n=k+1时的代数式比n=k时的代数式增加(或减少)的项.
这时一定要弄清三点:
①代数式从哪一项(哪一个数)开始,即第一项.
②代数式相邻两项之间的变化规律.
③代数式中最后一项(最后一个数)与n的关系.
1.求证:12-22+32-42+…+(2n-1)2-(2n)2=-n(2n+1)(n∈N+).
证明:(1)当n=1时,左边=12-22=-3,右边=-3,等式成立.
(2)假设当n=k时,等式成立,
即12-22+32-42+…+(2k-1)2-(2k)2=-k(2k+1).
当n=k+1时,
12-22+32-42+…+(2k-1)2-(2k)2+(2k+1)2-(2k+2)2
=-k(2k+1)+(2k+1)2-(2k+2)2=-k(2k+1)-(4k+3)
=-(2k2+5k+3)=-(k+1)[2(k+1)+1],
所以n=k+1时,等式也成立.
综上所述,等式对任何n∈N+都成立.
练一练
(拓展)题型 3 用数学归纳法证明几何问题
例 3 有n个圆,任意两个圆都相交于两点,任意三个圆不相交于同一 点,求证:这n个圆将平面分成f(n)=n2-n+2个部分(n∈N+).
典例剖析
证明:①当n=1时,一个圆将平面分成两个部分,且f(1)=1-1+2=2,所以n=1时命题成立.
②假设n=k(k≥1)时命题成立.
即k个圆把平面分成f(k)=k2-k+2个部分.
则n=k+1时,在k+1个圆中任取一个圆O,剩下的k个圆将平面分成f(k)个部分,而圆O与k个圆有2k个交点,这2k个点将圆O分成2k段弧,每段弧将原平面一分为二,故得f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2.
所以当n=k+1时,命题成立.
综合①②可知,对一切n∈N+,命题成立.
概念归纳
方法总结:
对于几何问题的证明,可以从有限情形中归纳出一个变化的过程,或者说体会出是怎么变化的,然后再去证明,也可以采用递推的办法,利用数学归纳法证明几何问题时,关键是正确分析由n=k到n=k+1时几何图形的变化规律.
练一练
相对于证明,人们往往对等式右边的结论是如何想出来的感到为难.
3.归纳—猜想—证明
新知探究
由表中数据,我们可以猜想:
n 1 2 3 4 5 ··· n
1 3 6 10 15 ···
1 5 14 30 55 ··· ?
···
再看一个例子:前n个正整数的立方和表达式是怎样的?
n 1 2 3 4 ··· n
1 3 6 10 ···
1 9 36 100 ··· ?
由表中数据,我们可以猜想:
一般来说,上述结论不是由数学归纳法发现出来的,而是通过观察具体实例
“猜想”出来的,然后用数学归纳法来验证这个猜想.
典例剖析
题型 2 归纳—猜想—证明
概念归纳
方法总结:
(1)利用数学归纳法可以探索与正整数n有关的未知问题、存在性问题,其基本模式是“归纳—猜想—证明”.
(2)“归纳—猜想—证明”的基本步骤是“试验—归纳—猜想—证明”.高中阶段与数列结合的问题是最常见的问题.这种方法更适用于已知数列的递推公式求通项公式.
练一练
练一练
1.用数学归纳法证明凸n边形的内角和公式时,由n=k到n=k+1的凸n边形的内角和增加( )
随堂练
2.用数学归纳法证明n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2(n∈N+)时,若记f(n)=n+(n+1)+(n+2)+…+(3n-2),则f(k+1)-f(k)等于( )
A.3k-1 B.3k+1
C.8k D.9k
B
C
3.以下是一个证明的全部过程:假设当n=k(k∈N+)时等式成立,即2+4+…+2k=k2+k,则当n=k+1时,2+4+…+2k+2(k+1)=k2+k+2(k+1)=(k+1)2+(k+1),即当n=k+1时,等式也成立.因此等式对于任何n∈N+都成立.
则用数学归纳法证明“2+4+…+2n=n2+n(n∈N+)”的过程中的错误为____________________________.
缺少当n=1时命题成立的证明
随堂练
4.用数学归纳法证明关于n的恒等式,当n=k时,等式为1×4+2×7+…+k(3k+1)=k(k+1)2,则当n=k+1时,等式为___________________________________________________.
1×4+2×7+…+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)2
随堂练
( )
1.用数学归纳法证明“1+2+22+…+2n+2=2n+3-1”,在验证n=1时,左边计算所得的式子为( )
A.1 B.1+2
C.1+2+22 D.1+2+22+23
分层练习-基础
D
B
A.n=k+1时等式成立
B.n=k+2时等式成立
C.n=2k+2时等式成立
D.n=2(k+2)时等式成立
分层练习-基础
( )
B
4.如果1×2×3+2×3×4+3×4×5+…+n(n+1)·(n+2)= n(n+1)(n+a)(n+b)对一切正整数n都成立,则a,b的值应该等于( )
A.a=1,b=3 B.a=-1,b=1
C.a=1,b=2 D.a=2,b=3
分层练习-基础
D
5.若等式A(n)(n∈N+)在n=k(k∈N+)时成立,则有n=k+1时等式也成立.现知等式对n=n0(n0∈N+)成立,则有( )
A.等式对所有正整数都成立
B.等式对小于n0的正整数不成立,对大于或等于n0的正整数都成立
C.等式对小于n0的正整数成立与否不能确定,对大于或等于n0的正整数
都成立
D.以上说法都不正确
分层练习-基础
C
分层练习-基础
( )
D
7.用数学归纳法证明1+2+22+…+2n-1=2n-1(n∈N+)的过程如下:
①当n=1时,左边=1,右边=21-1=1,左边=右边,等式成立.
②假设当n=k时,等式成立,即1+2+22+…+2k-1=2k-1,则当n=k+1时,1+2+22+…+2k-1+2k= =2k+1-1,
所以当n=k+1时,等式成立.
由此可知,对任何n∈N+等式都成立.上述证明的错误是______________
___________.
没有用归纳假
设进行递推
分层练习-基础
8.若f(n)=12+22+32+…+(2n)2,则f(k+1)与f(k)的递推关系式是______________________________.
f(k+1)=f(k)+(2k+1)2+(2k+2)2
分层练习-基础
9.用数学归纳法证明:
等式成立.
(2)假设当n=k(k≥2,k∈N+)时等式成立,
那么当n=k+1时,有
分层练习-基础
10.设a>0,f(x)= ,令a1=1,an+1=f(an),n∈N+.
(1)写出a2,a3,a4的值,并猜想{an}的通项公式;
分层练习-基础
因为a1=1,an+1=f(an),
(2)用数学归纳法证明你的结论.
分层练习-基础
①易知当n=1时,等式成立;
即当n=k+1时,等式也成立.
11.(多选)已知一个命题p(k),k=2n(n∈N+),若当n=1,2,…,1 000时,p(k)成立,且当n=1 001时也成立,则下列判断中正确的是( )
A.p(k)对k=528成立
B.p(k)对每一个自然数k都成立
C.p(k)对每一个正偶数k都成立
D.p(k)对某些偶数可能不成立
分层练习-基础
A、D
12.用数学归纳法证明(n+1)(n+2)·…·(n+n)=2n·1·3…·(2n-1)(n∈N+)时,将“n=k→n=k+1”两边同乘一个代数式,它是( )
分层练习-基础
D
分层练习-基础
14.已知1+2×3+3×32+4×33+…+n·3n-1=3n(na-b)+c对一切n∈N+
成立,那么a=____,b=_____,c=_____.
15.用数学归纳法证明:1+2+22+23+…+25n-1(n∈N+)是31的倍数,当n=1时,原式为________________,从n=k到n=k+1时需增添的项是____________________.
1+2+22+23+24
25k+25k+1+…+25k+4
分层练习-拓展
16.设函数y=f(x),对任意实数x,y都有f(x+y)=f(x)+f(y)+2xy.
(1)求f(0)的值;
令x=y=0,得f(0+0)=f(0)+f(0)+2×0×0,得f(0)=0.
(2)若f(1)=1,求f(2),f(3),f(4)的值;
由f(1)=1,
得f(2)=f(1+1)=f(1)+f(1)+2×1×1=4;
f(3)=f(2+1)=f(2)+f(1)+2×2×1=9;
f(4)=f(3+1)=f(3)+f(1)+2×3×1=16.
分层练习-拓展
(3)在(2)的条件下,猜想f(n)(n∈N+)的表达式并用数学归纳法加以证明.
由(2)可猜想f(n)=n2.
用数学归纳法证明如下:
①当n=1时,等式成立.
②假设当n=k(k≥1,k∈N+)时,f(n)=n2成立,
即f(k)=k2,
则当n=k+1时,f(k+1)=f(k)+f(1)+2×k×1=k2+1+2k=(k+1)2,
即当n=k+1时f(n)=n2也成立,
由①②可知,f(n)=n2对一切n∈N+都成立.
分层练习-拓展
课堂小结
1.知识清单:
(1)数学归纳法的概念.
(2)用数学归纳法证明等式.
(3)“归纳—猜想—证明”问题.
2.方法归纳:数学归纳法.
3.常见误区:①是对n0取值的问题易出错;
②是增加或减少的项数易出错.
湘教版2019高一数学(选修一) 第一章 数列
*1.4 数学归纳法
学习目标
1.了解数学归纳法的原理
2.利用数学归纳法证明等式
3.归纳—猜想—证明
情景导入
如果从盒子里拿出5个小球,发现全部都是绿色的,
是否判断盒子里面的小球都是绿色的?
不能.通过考察部分对象,得到一般的结论的方法,叫不完全归纳法.
不完全归纳法得到的结论不一定正确.
在多米诺骨牌游戏中,我们该如何保证所有的骨牌全部倒下?
要确保任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块滑牌也倒下,这样的话,只需要第一块骨牌倒下,就可导致后面所有的骨牌都能倒下.
情景导入
1.数学归纳法的概念
新知探究
本章研究了大量与正整数 n 有关的数列问题.
请你尝试解决下列问题:
通过对n=1,2,3,4进行归纳,可以猜想数列的通项公式是:
像这样由特殊到一般的推理方法,叫作归纳法.
用归纳法可以帮助我们从一些具体事例中发现一般规律.
当然,仅根据有限的特殊事例归纳得出的结论有时是不正确的.
例如“n +n+11是质数”这个命题对于n=1,2,3,…,9都成立,但当n=10时,10 +10+11=121=11 ,是一个合数.
概念归纳
大家熟悉的“多米诺骨牌效应”或许能给我们以启发.
将骨牌竖立起来摆成一排,并确保任意相邻的两块骨牌,若前一块骨牌倒下,则一定导致后一块骨牌也倒下.若推倒第一块骨牌,它会带倒第二块,再带倒第三块,以此类推,直到所有骨牌全部倒下.
如何找到这样一种推理方法呢?
(1)(奠基)最初的一个命题正确,
(2)(递推)由每一个命题的正确性都可以推出它的下一个命题的正确性,那么便证明了这一系列命题的正确性.
第一步奠基,
证明最初一个命题正确,相当于我们已经亲手“推倒第一块骨牌”.
第二步递推,
意味着“每一块倒下的骨牌怎样将下一块骨牌带倒”.
这样一来,无论有多少块骨牌,只要保证(1)和(2)成立,那么所有的骨牌一定都会倒下.
概念归纳
注意点:
初始值n0选择不一定是1,要结合题意恰当的选择.
(1)用数学归纳法证明:1+2+…+(2n+1)=(n+1)(2n+1),在验证n=1成立时,左边所得的代数式是( )
A.1 B.1+3
C.1+2+3 D.1+2+3+4
当n=1时,2n+1=2×1+1=3,所以左边为1+2+3.
典例剖析
C
(2)用数学归纳法证明1+2+3+…+n2= ,则当n=k+1时,等式左边应在n=k的基础上加上___________________________.
当n=k时,等式左边=1+2+3+…+k2,
当n=k+1时,
等式左边=1+2+3+…+k2+(k2+1)+(k2+2)+…+(k+1)2,
所以在n=k时的左边应加上(k2+1)+(k2+2)+…+(k+1)2.
(k2+1)+(k2+2)+…+(k+1)2
数学归纳法的三个关键点
(1)验证是基础:找准起点,奠基要稳,有些问题中验证的初始值不一定是1.
(2)递推是关键:数学归纳法的实质在于递推,要正确分析式子中项数的变化,弄清式子两边的构成规律.
(3)利用假设是核心:在第二步证明n=k+1时,一定要利用归纳假设.
练一练
所以当n=k+1时,不等式成立,则上述证法( )
A.过程全部正确
B.n=1验证不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
D
2.利用数学归纳法证明等式
新知探究
课本例题
例 2 用数学归纳法证明:
这表明,当n=k+1时,等式也成立.
课本例题
典例剖析
题型 1 用数学归纳法证明等式问题
概念归纳
用数学归纳法证明等式的策略
应用数学归纳法证明等式时需要确定两个式子的结构,即:
(1)n=n0时,等式的结构.
(2)n=k到n=k+1时,两个式子的结构:n=k+1时的代数式比n=k时的代数式增加(或减少)的项.
这时一定要弄清三点:
①代数式从哪一项(哪一个数)开始,即第一项.
②代数式相邻两项之间的变化规律.
③代数式中最后一项(最后一个数)与n的关系.
1.求证:12-22+32-42+…+(2n-1)2-(2n)2=-n(2n+1)(n∈N+).
证明:(1)当n=1时,左边=12-22=-3,右边=-3,等式成立.
(2)假设当n=k时,等式成立,
即12-22+32-42+…+(2k-1)2-(2k)2=-k(2k+1).
当n=k+1时,
12-22+32-42+…+(2k-1)2-(2k)2+(2k+1)2-(2k+2)2
=-k(2k+1)+(2k+1)2-(2k+2)2=-k(2k+1)-(4k+3)
=-(2k2+5k+3)=-(k+1)[2(k+1)+1],
所以n=k+1时,等式也成立.
综上所述,等式对任何n∈N+都成立.
练一练
(拓展)题型 3 用数学归纳法证明几何问题
例 3 有n个圆,任意两个圆都相交于两点,任意三个圆不相交于同一 点,求证:这n个圆将平面分成f(n)=n2-n+2个部分(n∈N+).
典例剖析
证明:①当n=1时,一个圆将平面分成两个部分,且f(1)=1-1+2=2,所以n=1时命题成立.
②假设n=k(k≥1)时命题成立.
即k个圆把平面分成f(k)=k2-k+2个部分.
则n=k+1时,在k+1个圆中任取一个圆O,剩下的k个圆将平面分成f(k)个部分,而圆O与k个圆有2k个交点,这2k个点将圆O分成2k段弧,每段弧将原平面一分为二,故得f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2.
所以当n=k+1时,命题成立.
综合①②可知,对一切n∈N+,命题成立.
概念归纳
方法总结:
对于几何问题的证明,可以从有限情形中归纳出一个变化的过程,或者说体会出是怎么变化的,然后再去证明,也可以采用递推的办法,利用数学归纳法证明几何问题时,关键是正确分析由n=k到n=k+1时几何图形的变化规律.
练一练
相对于证明,人们往往对等式右边的结论是如何想出来的感到为难.
3.归纳—猜想—证明
新知探究
由表中数据,我们可以猜想:
n 1 2 3 4 5 ··· n
1 3 6 10 15 ···
1 5 14 30 55 ··· ?
···
再看一个例子:前n个正整数的立方和表达式是怎样的?
n 1 2 3 4 ··· n
1 3 6 10 ···
1 9 36 100 ··· ?
由表中数据,我们可以猜想:
一般来说,上述结论不是由数学归纳法发现出来的,而是通过观察具体实例
“猜想”出来的,然后用数学归纳法来验证这个猜想.
典例剖析
题型 2 归纳—猜想—证明
概念归纳
方法总结:
(1)利用数学归纳法可以探索与正整数n有关的未知问题、存在性问题,其基本模式是“归纳—猜想—证明”.
(2)“归纳—猜想—证明”的基本步骤是“试验—归纳—猜想—证明”.高中阶段与数列结合的问题是最常见的问题.这种方法更适用于已知数列的递推公式求通项公式.
练一练
练一练
1.用数学归纳法证明凸n边形的内角和公式时,由n=k到n=k+1的凸n边形的内角和增加( )
随堂练
2.用数学归纳法证明n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2(n∈N+)时,若记f(n)=n+(n+1)+(n+2)+…+(3n-2),则f(k+1)-f(k)等于( )
A.3k-1 B.3k+1
C.8k D.9k
B
C
3.以下是一个证明的全部过程:假设当n=k(k∈N+)时等式成立,即2+4+…+2k=k2+k,则当n=k+1时,2+4+…+2k+2(k+1)=k2+k+2(k+1)=(k+1)2+(k+1),即当n=k+1时,等式也成立.因此等式对于任何n∈N+都成立.
则用数学归纳法证明“2+4+…+2n=n2+n(n∈N+)”的过程中的错误为____________________________.
缺少当n=1时命题成立的证明
随堂练
4.用数学归纳法证明关于n的恒等式,当n=k时,等式为1×4+2×7+…+k(3k+1)=k(k+1)2,则当n=k+1时,等式为___________________________________________________.
1×4+2×7+…+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)2
随堂练
( )
1.用数学归纳法证明“1+2+22+…+2n+2=2n+3-1”,在验证n=1时,左边计算所得的式子为( )
A.1 B.1+2
C.1+2+22 D.1+2+22+23
分层练习-基础
D
B
A.n=k+1时等式成立
B.n=k+2时等式成立
C.n=2k+2时等式成立
D.n=2(k+2)时等式成立
分层练习-基础
( )
B
4.如果1×2×3+2×3×4+3×4×5+…+n(n+1)·(n+2)= n(n+1)(n+a)(n+b)对一切正整数n都成立,则a,b的值应该等于( )
A.a=1,b=3 B.a=-1,b=1
C.a=1,b=2 D.a=2,b=3
分层练习-基础
D
5.若等式A(n)(n∈N+)在n=k(k∈N+)时成立,则有n=k+1时等式也成立.现知等式对n=n0(n0∈N+)成立,则有( )
A.等式对所有正整数都成立
B.等式对小于n0的正整数不成立,对大于或等于n0的正整数都成立
C.等式对小于n0的正整数成立与否不能确定,对大于或等于n0的正整数
都成立
D.以上说法都不正确
分层练习-基础
C
分层练习-基础
( )
D
7.用数学归纳法证明1+2+22+…+2n-1=2n-1(n∈N+)的过程如下:
①当n=1时,左边=1,右边=21-1=1,左边=右边,等式成立.
②假设当n=k时,等式成立,即1+2+22+…+2k-1=2k-1,则当n=k+1时,1+2+22+…+2k-1+2k= =2k+1-1,
所以当n=k+1时,等式成立.
由此可知,对任何n∈N+等式都成立.上述证明的错误是______________
___________.
没有用归纳假
设进行递推
分层练习-基础
8.若f(n)=12+22+32+…+(2n)2,则f(k+1)与f(k)的递推关系式是______________________________.
f(k+1)=f(k)+(2k+1)2+(2k+2)2
分层练习-基础
9.用数学归纳法证明:
等式成立.
(2)假设当n=k(k≥2,k∈N+)时等式成立,
那么当n=k+1时,有
分层练习-基础
10.设a>0,f(x)= ,令a1=1,an+1=f(an),n∈N+.
(1)写出a2,a3,a4的值,并猜想{an}的通项公式;
分层练习-基础
因为a1=1,an+1=f(an),
(2)用数学归纳法证明你的结论.
分层练习-基础
①易知当n=1时,等式成立;
即当n=k+1时,等式也成立.
11.(多选)已知一个命题p(k),k=2n(n∈N+),若当n=1,2,…,1 000时,p(k)成立,且当n=1 001时也成立,则下列判断中正确的是( )
A.p(k)对k=528成立
B.p(k)对每一个自然数k都成立
C.p(k)对每一个正偶数k都成立
D.p(k)对某些偶数可能不成立
分层练习-基础
A、D
12.用数学归纳法证明(n+1)(n+2)·…·(n+n)=2n·1·3…·(2n-1)(n∈N+)时,将“n=k→n=k+1”两边同乘一个代数式,它是( )
分层练习-基础
D
分层练习-基础
14.已知1+2×3+3×32+4×33+…+n·3n-1=3n(na-b)+c对一切n∈N+
成立,那么a=____,b=_____,c=_____.
15.用数学归纳法证明:1+2+22+23+…+25n-1(n∈N+)是31的倍数,当n=1时,原式为________________,从n=k到n=k+1时需增添的项是____________________.
1+2+22+23+24
25k+25k+1+…+25k+4
分层练习-拓展
16.设函数y=f(x),对任意实数x,y都有f(x+y)=f(x)+f(y)+2xy.
(1)求f(0)的值;
令x=y=0,得f(0+0)=f(0)+f(0)+2×0×0,得f(0)=0.
(2)若f(1)=1,求f(2),f(3),f(4)的值;
由f(1)=1,
得f(2)=f(1+1)=f(1)+f(1)+2×1×1=4;
f(3)=f(2+1)=f(2)+f(1)+2×2×1=9;
f(4)=f(3+1)=f(3)+f(1)+2×3×1=16.
分层练习-拓展
(3)在(2)的条件下,猜想f(n)(n∈N+)的表达式并用数学归纳法加以证明.
由(2)可猜想f(n)=n2.
用数学归纳法证明如下:
①当n=1时,等式成立.
②假设当n=k(k≥1,k∈N+)时,f(n)=n2成立,
即f(k)=k2,
则当n=k+1时,f(k+1)=f(k)+f(1)+2×k×1=k2+1+2k=(k+1)2,
即当n=k+1时f(n)=n2也成立,
由①②可知,f(n)=n2对一切n∈N+都成立.
分层练习-拓展
课堂小结
1.知识清单:
(1)数学归纳法的概念.
(2)用数学归纳法证明等式.
(3)“归纳—猜想—证明”问题.
2.方法归纳:数学归纳法.
3.常见误区:①是对n0取值的问题易出错;
②是增加或减少的项数易出错.
同课章节目录
