湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.4直线的方向向量与法向量课件(共34张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.4直线的方向向量与法向量课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:43:11 | ||
图片预览











文档简介
(共34张PPT)
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2 直线的方程
2.2.4 直线的方向向量与法向量
学习目标
1.了解直线的方向向量与法向量(重点)
2.会利用直线的方向向量与法向量求直线的方程(难点)
3.体会数形结合,分类讨论,特殊到一般等数学思想(重点)
名称 已知条件 方程 适用范围
点斜式 过点 P0(x0, y0),斜率为 k
斜截式 纵截距为 b,
斜率为 k
两点式 过点P1(x1,y1),P2(x2,y2)
截距式 横截距和纵截距分别为 a 和 b
一般式
y -y0 = k (x-x0)
y = k x + b
(y2-y1)(x-x1)-(x2-x1)(y-y1)=0
不表示垂直x轴的直线
即斜率不存在的直线
所有直线
不表示垂直于坐标轴和经过原点的直线
不表示垂直x轴的直线
即斜率不存在的直线
Ax十By+C=0(A,B不同时为0)
所有直线
复习导入
本章一开始就用直线的斜率(倾斜程度)来表示直线的方向.那么,什么叫作直线PQ的方向?
直线上两个不同点PQ之间的有向线段的方向就
是直线的方向,可以用非零向量PQ来表示.
不过,我们没有把直线 l 规定成有向直线,直线PQ与QP是同一条直线,两个相反向量PQ,QP的
方向都代表直线 l 的方向,此时这两个方向平行.
1.直线的方向向量
新知探究
A
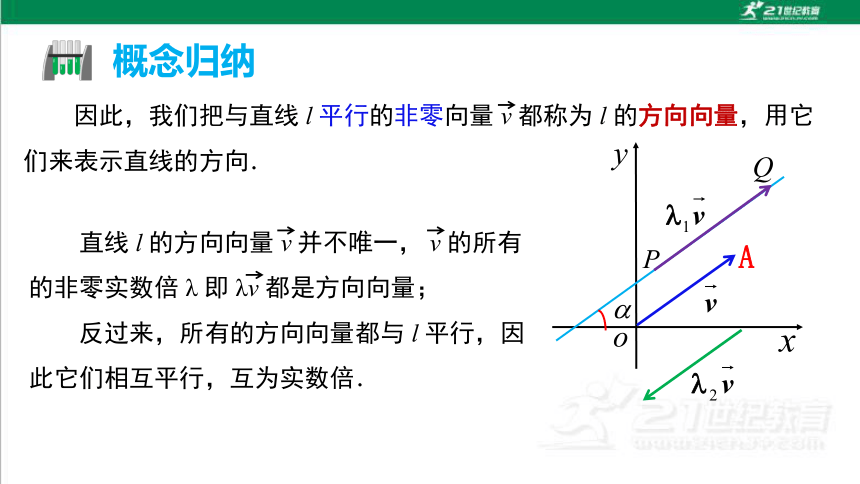
直线 l 的方向向量 v 并不唯一, v 的所有的非零实数倍 λ 即 λv 都是方向向量;
反过来,所有的方向向量都与 l 平行,因此它们相互平行,互为实数倍.
因此,我们把与直线 l 平行的非零向量 v 都称为 l 的方向向量,用它们来表示直线的方向.
概念归纳
课本例7 求直线y=kx+b的全体方向向量.
其中λ=x2-x1可以取任意非零实数.
典例剖析
1.求直线4x-y+5=0的全体方向向量.
将直线4x-y+5=0化为斜截式为y=4x+5,
其斜率k=4,
因此,该直线的全体方向向量为λ(1,4),其中λ为任意非零实数.
练一练
课本例8 求直线3x+4y-12=0的全体方向向量.
解: (方法一)直线方程化为斜截式,得:
其中λ 为任意非零实数.
斜率为k的直线的方向向量为(1,k)的非零实数倍.
其斜率为 .
典例剖析
课本例8 求直线3x+4y-12=0的全体方向向量.
解: (方法二)直线上任意两点P(x0, y0) ,Q(x,y)的坐标满足等式:
3x0+4y0-12=0, ① 3x+4y-12=0. ②
②-①得 3(x-x0)+4(y-y0) = 0. ③
将③式的左边写出数量积的形式,得 (3,4) (x-x0,y-y0) = 0. ④
当PQ不重合时,PQ =(x-x0,y-y0),代表了直线的全体方向向量,
由④可知,PQ与向量(3,4)垂直,因此这条直线与向量(3,4)垂直.
由3×4+4×( 3)=0得到向量(4, 3)与向量(3,4)垂直.因此(4, 3)是
直线的一个方向向量,直线的全体方向向量为λ(4, 3) = (4λ, 3λ),其中λ为任意非零实数.
课本例8方法二的推理适用于一般直线方程 Ax+By+C=0 (A,B不同时为0).
解:直线上任意两点P(x0, y0) ,Q(x,y)的坐标满足等式:
Ax0+By0+C=0, Ax+By+C=0.
以上两个式子相减,得 A(x-x0)+B(y-y0) = 0.
将上式的左边写出数量积的形式,得 (A,B) (x-x0,y-y0) = 0.
该式可看成向量n = (A,B)与向量PQ =(x-x0,y-y0)的数量积.
即: n PQ=0,用几何语言描述就是n⊥PQ.
这说明过定点P及任意点Q的线段垂直于n = ON ,动点Q组成的图形就是过定点P且与ON垂直的直线l .
2.直线的法向量
新知探究
反之,作与直线l垂直的非零有向线段ON我们取向量n = ON =(A,B).
已知直线l上一个定点P(x0, y0),则平面上任一点Q(x,y)在直线上的充分必要条件为ON⊥PQ.
用向量运算叙述出来就是:
ON PQ = 0 (A,B) (x-x0,y-y0) = 0
A(x-x0)+B(y-y0) = 0.
由此得到直线l的方程:
A(x-x0)+B(y-y0) = 0.
当P,Q不重合时,PQ =(x-x0,y-y0),代表了直线l的全体方向向量,所以向量(A,B)垂直于直线的全体方向向量.
当P,Q两点重合时(x-x0,y-y0) = (0,0)是零向量,不是方向向量,仍与向量(A,B)垂直.
因此,(x-x0,y-y0),代表了直线l的全体方向向量,它们都与向量(A,B)垂直.
因此,非零向量(A,B)与直线l垂直.
与直线 l 垂直的非零向量(A,B)称为直线 l 的法向量.
直线的一般式方程 Ax+By+C=0的一次项系数组成的向量(A,B)是直
线的法向量.
反过来,已知直线的法向量(A,B),就知道了一般式方程 Ax+By+C=0的一次项系数.将直线上任一已知点(x0, y0)的坐标代入该方程,就可由Ax0+B y0+C=0得到待定常数C=-Ax0-B y0,进而得到直线方程
Ax+By-Ax0-B y0=0.
即 A(x-x0)+B(y-y0) = 0的形式.
概念归纳
2.若直线l的倾斜角为135°,则直线l的一个法向量是( )
A.(1,-1) B.(1,1)
C.(-1,1) D.(2, )
∵直线l的倾斜角为135°,∴直线l的斜率k=-1,
∴直线l的一个方向向量为(1,-1),则直线l的一个法向量为(1,1).
B
练一练
课本例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (1)(方法一)设点(x,y)为直线上不同于点A的任意一点,直线的方
向向量(x-2,y-1)垂直于向量(3,2),则有
(3,2) (x-2,y-1) = 3(x-2)+2(y-1)=0.
整理得一般式方程
3x+2y-8=0.
典例剖析
例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (1) (方法二)由条件可知向量(3,2)为所求直线的法向量,故可设直
线的一般式方程为
3x+2y+C=0.
将点A(2,1)的坐标代入上述方程,得:
3×3+2×1+C=0
解得: C=-8.
因此直线方程为:3x+2y-8=0.
例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (2)由已知条件可知直线的方向向量AB = (5-2,2-1)=(3,1).
因此,可设直线的一般式方程为
x-3y+C=0.
将点A(2,1)的坐标代入上述方程,得:
1×2-3×1+C=0,
解得:C=1.
因此直线方程为: x-3y+1=0.
又1×3+( 3)×1=0,可知直线的法向量为:n =(1,-3).
题型1 求直线的方向向量和法向量
例1 (1)求直线2x-3y+5=0的一个方向向量和法向量;
(2)求过点A(2,3)和点B(0, -2)的直线的一个方向向量和法向量.
典例剖析
熟练掌握直线的斜截式(或一般式)方程对应的方向向量的坐标特征.不同形式的直线方程,可以先将方程化为斜截式或一般式,然后直接写出它的一个方向向量.
直线l:y=kx+b的一个方向向量为v=(1,k);
直线l:Ax+By+C=0的一个方向向量为v=(B,-A).
总结归纳
解析:直线l的斜率为k=tan 135°=-1,
所以直线l的全体方向向量为λ(1,-1),(λ≠0,λ∈R)
检验可知B、C为直线l的方向向量.
BC
练一练
(2)若直线l经过点A(-1,4),B(3,2),则直线的一个法向量n为( )
A.n=(1,-2) B.n=(4,-2)
C.n=(4,2) D.n=(1,2)
D
练一练
题型2 直线方向向量的应用
例2 (1)经过A(0,2),B(-1,0)两点的直线的方向向量为(1,k),求k的值;
(2)如果直线过点P(1,-4),且直线的方向向量是a=(3,9),求直线的方程.
典例剖析
已知直线的方向向量求直线方程时,可用待定系数法求得:
(1)若已知直线的一个方向向量为v=(1,k),则可设直线l的方程为y=kx+b;
(2)若已知直线的一个方向向量为v=(B,-A),则可设直线l的方程为Ax+By+C=0.
总结归纳
B
练一练
(2)平行于向量(2,-3)且经过点B(1,-2)的直线方程为_______________.
3x+2y+1=0
解析: 由条件可设直线的方程为3x+2y+C=0,
把点B(1,-2)代入得C=1,
所以所求直线方程为3x+2y+1=0.
练一练
题型3 直线法向量的应用
例3 (1)已知两条直线l1:ax-2y-3=0,l2:4x+6y-3=0,若l1的一个法向量恰为l2的一个方向向量,则a=____;
3
解析:因为直线l1:ax-2y-3=0的一个法向量恰为l2:4x+6y-3=0的一个方向向量,所以l1⊥l2,所以a×4+(-2)×6=0,解得:a=3.
典例剖析
(2)如果直线过点D(6,-1),且直线的法向量是b=(4,-3),求直线的方程.
典例剖析
总结归纳
已知直线的法向量求直线方程的方法
待定系数法:若已知直线的一个法向量为n=(A,B),则可设直线l的方程为Ax+By+C=0.
D
练一练
(2)垂直于向量(3,-5)且经过点A(1,2)的直线方程为 _________ 。
3x-5y+7=0
解析: 由条件可知向量(3,-5)为所求直线的一个法向量,
故可设直线的一般式方程为3x-5y+C=0,
将点A(1,2)代入得C=7,
所以直线方程为3x-5y+7=0.
练一练
1.判断正误(正确的画“√”,错误的画“×”)
(1)零向量不能作为直线的方向向量和平面的法向量.( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量.( )
(3)若n为直线l的一个法向量,则λn(λ≠0)也是直线l的一个法向量.( )
(4)向量(x0,y0)与(y0,-x0)是相互垂直的.( )
√
√
√
×
随堂练习
2.直线3x-2y-1=0的一个方向向量为( )
A.(2,-3) B.(2,3) C.(-3,2) D.(3,2)
B
3.直线3x-4y+5=0的一个法向量是( )
A.(3,4) B.(3,-4) C.(4,3) D.(4,-3)
B
4.已知直线l的方向向量为(1,5),则直线l的法向量为( )
A.(5,1) B.(-1,5) C.(5,-1) D.(-5,-1)
解析:因为直线l的方向向量为(1,5),所以直线l的法向量可以是(-5,1)或(5,-1).
C
6.若一条直线的斜率为k,则它的一个方向向量是________,一个法向量是________.
(1,k)
(k,-1)
解析:因为直线的斜率为k,所以它的一个方向向量为(1,k),设一个法向量为(x,y),则(x,y)·(1,k)=x+ky=0,不妨取x=k,y=-1,则它的一个法向量是(k,-1).
5.直线的一个方向向量为v=(1,-3),且经过点(0,2),则直线的方程为( )
A.3x-y+2=0 B.3x+y-2=0
C.3x+y+2=0 D.3x-y-2=0
B
方法一 ∵直线的一个方向向量为v=(1,-3),∴k=-3,
∴直线的方程为y=-3x+2,
即3x+y-2=0.
方法二 由题意知直线的一个法向量为n=(3,1),∴直线的方程可设为3x+y+C=0,将点(0,2)代入得C=-2,故所求直线的方程为3x+y-2=0.
直线的方向向量:
与直线平行的非零向量都称为的方向向量.
斜率为k的直线的方向向量为(1,k)的非零实数倍.
直线 Ax+By+C=0 (A,B不同时为0)的一个方向向量为 (B,-A).
直线的法向量:
与直线垂直的非零向量称为直线的法向量.
直线 Ax+By+C=0 (A,B不同时为0)的一个法向量为 (A,B).
过点(x0, y0),且法向量为(A,B)的直线的方程为A(x-x0)+B(y-y0) = 0.
课堂小结
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2 直线的方程
2.2.4 直线的方向向量与法向量
学习目标
1.了解直线的方向向量与法向量(重点)
2.会利用直线的方向向量与法向量求直线的方程(难点)
3.体会数形结合,分类讨论,特殊到一般等数学思想(重点)
名称 已知条件 方程 适用范围
点斜式 过点 P0(x0, y0),斜率为 k
斜截式 纵截距为 b,
斜率为 k
两点式 过点P1(x1,y1),P2(x2,y2)
截距式 横截距和纵截距分别为 a 和 b
一般式
y -y0 = k (x-x0)
y = k x + b
(y2-y1)(x-x1)-(x2-x1)(y-y1)=0
不表示垂直x轴的直线
即斜率不存在的直线
所有直线
不表示垂直于坐标轴和经过原点的直线
不表示垂直x轴的直线
即斜率不存在的直线
Ax十By+C=0(A,B不同时为0)
所有直线
复习导入
本章一开始就用直线的斜率(倾斜程度)来表示直线的方向.那么,什么叫作直线PQ的方向?
直线上两个不同点PQ之间的有向线段的方向就
是直线的方向,可以用非零向量PQ来表示.
不过,我们没有把直线 l 规定成有向直线,直线PQ与QP是同一条直线,两个相反向量PQ,QP的
方向都代表直线 l 的方向,此时这两个方向平行.
1.直线的方向向量
新知探究
A
直线 l 的方向向量 v 并不唯一, v 的所有的非零实数倍 λ 即 λv 都是方向向量;
反过来,所有的方向向量都与 l 平行,因此它们相互平行,互为实数倍.
因此,我们把与直线 l 平行的非零向量 v 都称为 l 的方向向量,用它们来表示直线的方向.
概念归纳
课本例7 求直线y=kx+b的全体方向向量.
其中λ=x2-x1可以取任意非零实数.
典例剖析
1.求直线4x-y+5=0的全体方向向量.
将直线4x-y+5=0化为斜截式为y=4x+5,
其斜率k=4,
因此,该直线的全体方向向量为λ(1,4),其中λ为任意非零实数.
练一练
课本例8 求直线3x+4y-12=0的全体方向向量.
解: (方法一)直线方程化为斜截式,得:
其中λ 为任意非零实数.
斜率为k的直线的方向向量为(1,k)的非零实数倍.
其斜率为 .
典例剖析
课本例8 求直线3x+4y-12=0的全体方向向量.
解: (方法二)直线上任意两点P(x0, y0) ,Q(x,y)的坐标满足等式:
3x0+4y0-12=0, ① 3x+4y-12=0. ②
②-①得 3(x-x0)+4(y-y0) = 0. ③
将③式的左边写出数量积的形式,得 (3,4) (x-x0,y-y0) = 0. ④
当PQ不重合时,PQ =(x-x0,y-y0),代表了直线的全体方向向量,
由④可知,PQ与向量(3,4)垂直,因此这条直线与向量(3,4)垂直.
由3×4+4×( 3)=0得到向量(4, 3)与向量(3,4)垂直.因此(4, 3)是
直线的一个方向向量,直线的全体方向向量为λ(4, 3) = (4λ, 3λ),其中λ为任意非零实数.
课本例8方法二的推理适用于一般直线方程 Ax+By+C=0 (A,B不同时为0).
解:直线上任意两点P(x0, y0) ,Q(x,y)的坐标满足等式:
Ax0+By0+C=0, Ax+By+C=0.
以上两个式子相减,得 A(x-x0)+B(y-y0) = 0.
将上式的左边写出数量积的形式,得 (A,B) (x-x0,y-y0) = 0.
该式可看成向量n = (A,B)与向量PQ =(x-x0,y-y0)的数量积.
即: n PQ=0,用几何语言描述就是n⊥PQ.
这说明过定点P及任意点Q的线段垂直于n = ON ,动点Q组成的图形就是过定点P且与ON垂直的直线l .
2.直线的法向量
新知探究
反之,作与直线l垂直的非零有向线段ON我们取向量n = ON =(A,B).
已知直线l上一个定点P(x0, y0),则平面上任一点Q(x,y)在直线上的充分必要条件为ON⊥PQ.
用向量运算叙述出来就是:
ON PQ = 0 (A,B) (x-x0,y-y0) = 0
A(x-x0)+B(y-y0) = 0.
由此得到直线l的方程:
A(x-x0)+B(y-y0) = 0.
当P,Q不重合时,PQ =(x-x0,y-y0),代表了直线l的全体方向向量,所以向量(A,B)垂直于直线的全体方向向量.
当P,Q两点重合时(x-x0,y-y0) = (0,0)是零向量,不是方向向量,仍与向量(A,B)垂直.
因此,(x-x0,y-y0),代表了直线l的全体方向向量,它们都与向量(A,B)垂直.
因此,非零向量(A,B)与直线l垂直.
与直线 l 垂直的非零向量(A,B)称为直线 l 的法向量.
直线的一般式方程 Ax+By+C=0的一次项系数组成的向量(A,B)是直
线的法向量.
反过来,已知直线的法向量(A,B),就知道了一般式方程 Ax+By+C=0的一次项系数.将直线上任一已知点(x0, y0)的坐标代入该方程,就可由Ax0+B y0+C=0得到待定常数C=-Ax0-B y0,进而得到直线方程
Ax+By-Ax0-B y0=0.
即 A(x-x0)+B(y-y0) = 0的形式.
概念归纳
2.若直线l的倾斜角为135°,则直线l的一个法向量是( )
A.(1,-1) B.(1,1)
C.(-1,1) D.(2, )
∵直线l的倾斜角为135°,∴直线l的斜率k=-1,
∴直线l的一个方向向量为(1,-1),则直线l的一个法向量为(1,1).
B
练一练
课本例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (1)(方法一)设点(x,y)为直线上不同于点A的任意一点,直线的方
向向量(x-2,y-1)垂直于向量(3,2),则有
(3,2) (x-2,y-1) = 3(x-2)+2(y-1)=0.
整理得一般式方程
3x+2y-8=0.
典例剖析
例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (1) (方法二)由条件可知向量(3,2)为所求直线的法向量,故可设直
线的一般式方程为
3x+2y+C=0.
将点A(2,1)的坐标代入上述方程,得:
3×3+2×1+C=0
解得: C=-8.
因此直线方程为:3x+2y-8=0.
例9 写出满足下列条件的直线的方程:
(1)垂直于向量(3,2)并且经过点A(2,1); (2)经过点A(2,1)和B(5,2).
解: (2)由已知条件可知直线的方向向量AB = (5-2,2-1)=(3,1).
因此,可设直线的一般式方程为
x-3y+C=0.
将点A(2,1)的坐标代入上述方程,得:
1×2-3×1+C=0,
解得:C=1.
因此直线方程为: x-3y+1=0.
又1×3+( 3)×1=0,可知直线的法向量为:n =(1,-3).
题型1 求直线的方向向量和法向量
例1 (1)求直线2x-3y+5=0的一个方向向量和法向量;
(2)求过点A(2,3)和点B(0, -2)的直线的一个方向向量和法向量.
典例剖析
熟练掌握直线的斜截式(或一般式)方程对应的方向向量的坐标特征.不同形式的直线方程,可以先将方程化为斜截式或一般式,然后直接写出它的一个方向向量.
直线l:y=kx+b的一个方向向量为v=(1,k);
直线l:Ax+By+C=0的一个方向向量为v=(B,-A).
总结归纳
解析:直线l的斜率为k=tan 135°=-1,
所以直线l的全体方向向量为λ(1,-1),(λ≠0,λ∈R)
检验可知B、C为直线l的方向向量.
BC
练一练
(2)若直线l经过点A(-1,4),B(3,2),则直线的一个法向量n为( )
A.n=(1,-2) B.n=(4,-2)
C.n=(4,2) D.n=(1,2)
D
练一练
题型2 直线方向向量的应用
例2 (1)经过A(0,2),B(-1,0)两点的直线的方向向量为(1,k),求k的值;
(2)如果直线过点P(1,-4),且直线的方向向量是a=(3,9),求直线的方程.
典例剖析
已知直线的方向向量求直线方程时,可用待定系数法求得:
(1)若已知直线的一个方向向量为v=(1,k),则可设直线l的方程为y=kx+b;
(2)若已知直线的一个方向向量为v=(B,-A),则可设直线l的方程为Ax+By+C=0.
总结归纳
B
练一练
(2)平行于向量(2,-3)且经过点B(1,-2)的直线方程为_______________.
3x+2y+1=0
解析: 由条件可设直线的方程为3x+2y+C=0,
把点B(1,-2)代入得C=1,
所以所求直线方程为3x+2y+1=0.
练一练
题型3 直线法向量的应用
例3 (1)已知两条直线l1:ax-2y-3=0,l2:4x+6y-3=0,若l1的一个法向量恰为l2的一个方向向量,则a=____;
3
解析:因为直线l1:ax-2y-3=0的一个法向量恰为l2:4x+6y-3=0的一个方向向量,所以l1⊥l2,所以a×4+(-2)×6=0,解得:a=3.
典例剖析
(2)如果直线过点D(6,-1),且直线的法向量是b=(4,-3),求直线的方程.
典例剖析
总结归纳
已知直线的法向量求直线方程的方法
待定系数法:若已知直线的一个法向量为n=(A,B),则可设直线l的方程为Ax+By+C=0.
D
练一练
(2)垂直于向量(3,-5)且经过点A(1,2)的直线方程为 _________ 。
3x-5y+7=0
解析: 由条件可知向量(3,-5)为所求直线的一个法向量,
故可设直线的一般式方程为3x-5y+C=0,
将点A(1,2)代入得C=7,
所以直线方程为3x-5y+7=0.
练一练
1.判断正误(正确的画“√”,错误的画“×”)
(1)零向量不能作为直线的方向向量和平面的法向量.( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量.( )
(3)若n为直线l的一个法向量,则λn(λ≠0)也是直线l的一个法向量.( )
(4)向量(x0,y0)与(y0,-x0)是相互垂直的.( )
√
√
√
×
随堂练习
2.直线3x-2y-1=0的一个方向向量为( )
A.(2,-3) B.(2,3) C.(-3,2) D.(3,2)
B
3.直线3x-4y+5=0的一个法向量是( )
A.(3,4) B.(3,-4) C.(4,3) D.(4,-3)
B
4.已知直线l的方向向量为(1,5),则直线l的法向量为( )
A.(5,1) B.(-1,5) C.(5,-1) D.(-5,-1)
解析:因为直线l的方向向量为(1,5),所以直线l的法向量可以是(-5,1)或(5,-1).
C
6.若一条直线的斜率为k,则它的一个方向向量是________,一个法向量是________.
(1,k)
(k,-1)
解析:因为直线的斜率为k,所以它的一个方向向量为(1,k),设一个法向量为(x,y),则(x,y)·(1,k)=x+ky=0,不妨取x=k,y=-1,则它的一个法向量是(k,-1).
5.直线的一个方向向量为v=(1,-3),且经过点(0,2),则直线的方程为( )
A.3x-y+2=0 B.3x+y-2=0
C.3x+y+2=0 D.3x-y-2=0
B
方法一 ∵直线的一个方向向量为v=(1,-3),∴k=-3,
∴直线的方程为y=-3x+2,
即3x+y-2=0.
方法二 由题意知直线的一个法向量为n=(3,1),∴直线的方程可设为3x+y+C=0,将点(0,2)代入得C=-2,故所求直线的方程为3x+y-2=0.
直线的方向向量:
与直线平行的非零向量都称为的方向向量.
斜率为k的直线的方向向量为(1,k)的非零实数倍.
直线 Ax+By+C=0 (A,B不同时为0)的一个方向向量为 (B,-A).
直线的法向量:
与直线垂直的非零向量称为直线的法向量.
直线 Ax+By+C=0 (A,B不同时为0)的一个法向量为 (A,B).
过点(x0, y0),且法向量为(A,B)的直线的方程为A(x-x0)+B(y-y0) = 0.
课堂小结
同课章节目录
