湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.1直线的点斜式方程课件(共43张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第2章平面解析几何初步2.2.1直线的点斜式方程课件(共43张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:45:04 | ||
图片预览









文档简介
(共43张PPT)
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2.1 直线的点斜式方程
2.2 直线的方程
学习目标
1.了解由斜率公式推导直线的点斜式方程的过程.
2.掌握直线的点斜式方程与斜截式方程.(重点)
3.会利用直线的点斜式方程与斜截式方程解决有关的问题.(难点)
情景导入
旧知回顾
上节课我们学习了直线的倾斜角与斜率,你能简述一下它们的概念吗?
直线的倾斜角:
当直线 l 与 x 轴相交时,我们把 x 轴正向绕交点逆时针旋转到与直线 l 向上方向首次重合所成的角 α 叫作直线 l 的倾斜角.
倾斜角的取值范围: 0 ≤ α < π.
你能在纸上默写出斜率公式吗?
斜率公式:经过两个不同点
A(x1,y1),B (x2,y2),(x1≠x2)
的直线的斜率为
情景导入
射击手在进行射击训练时,要掌握两个动作要领:
一是托枪的手要非常稳,
二是眼睛要瞄准目标的方向.
若把子弹飞行的轨迹看作一条直线,
并且射击手达到上述的两个动作要求,
试分析子弹是否会击中目标.
给定直线的斜率和直线上一点,或者给定两点,都能唯一确定一条直线.
本节,我们将用给定的条件,将直线上所有点的坐标(x,y)满足的共同关系表示出来,这就是直线方程.
1.直线的点斜式方程
新知探究
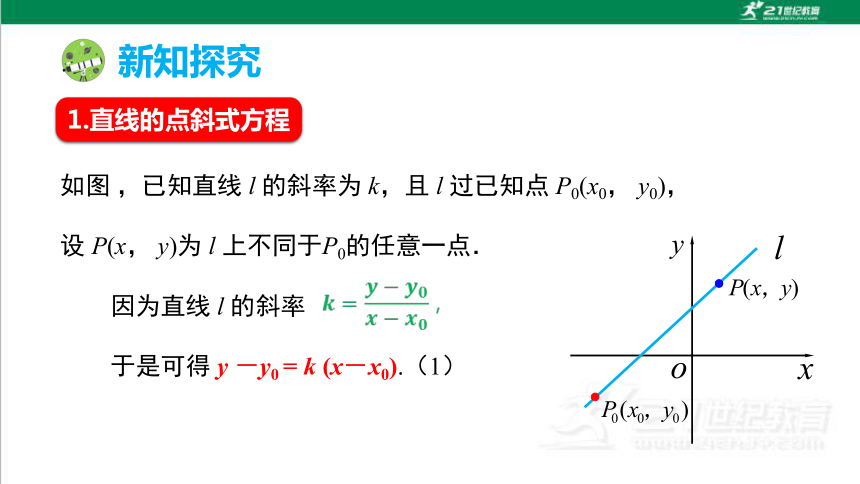
如图 ,已知直线 l 的斜率为 k,且 l 过已知点 P0(x0, y0),
设 P(x, y)为 l 上不同于P0的任意一点.
因为直线 l 的斜率
于是可得 y -y0 = k (x-x0).(1)
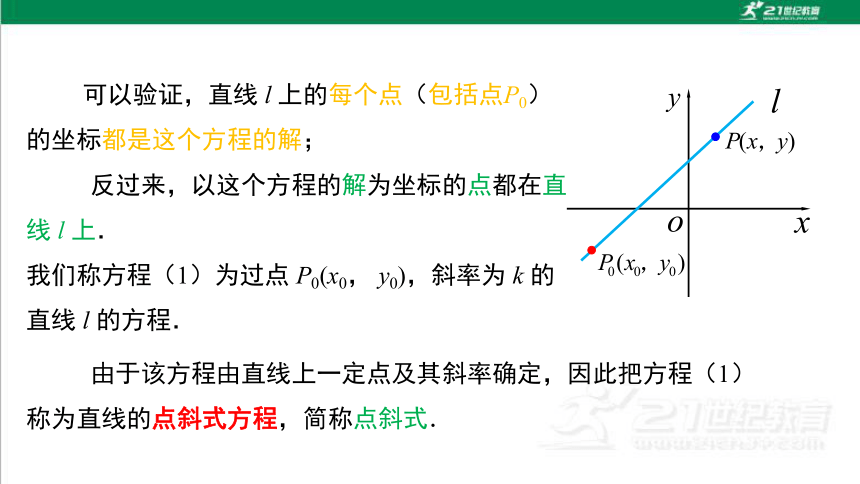
可以验证,直线 l 上的每个点(包括点P0)的坐标都是这个方程的解;
反过来,以这个方程的解为坐标的点都在直线 l 上.
我们称方程(1)为过点 P0(x0, y0),斜率为 k 的直线 l 的方程.
由于该方程由直线上一定点及其斜率确定,因此把方程(1)称为直线的点斜式方程,简称点斜式.
当直线 l 与 x 轴垂直时,斜率不存在,其方程不能用点斜式表示,但因为 l 上每一点的横坐标都等于x0,所以它的方程是 x = x0 .
综上可知,若直线 l 过点 P0(x0, y0),
当直线 l 与 x 轴不垂直时,斜率为 k,
那么直线 l 的方程为:y -y0 = k (x-x0).
特别地,当直线 l 与 x 轴平行或重合时,斜率 k=0,
直线 l 的方程为:y = y0 .
当直线 l 与 x 轴垂直时,斜率不存在,
直线 l 的方程为:x = x0 .
课本例1 已知直线l经过点P(2,3),斜率为2,求直线l的方程,并画出该直线.
经过点P(2,3),斜率为2的直线的点斜式方程是
y-3=2(x-2).
画该直线时,可在直线l上另取一点P1(x1,y1),
如取x1=1,y1=1,得P1(1,1),
过P,P1作直线即为所求,如右图.
课本例题
例 1 根据条件写出下列直线的点斜式方程:
(1)经过点A(-4,3),斜率k=3;
由点斜式方程可知,所求直线的点斜式方程为y-3=3(x+4).
典例剖析
(2)经过点B(-1,4),倾斜角为135°.
由题意知,直线的斜率k=tan 135°=-1,
故所求直线的点斜式方程为y-4=-(x+1).
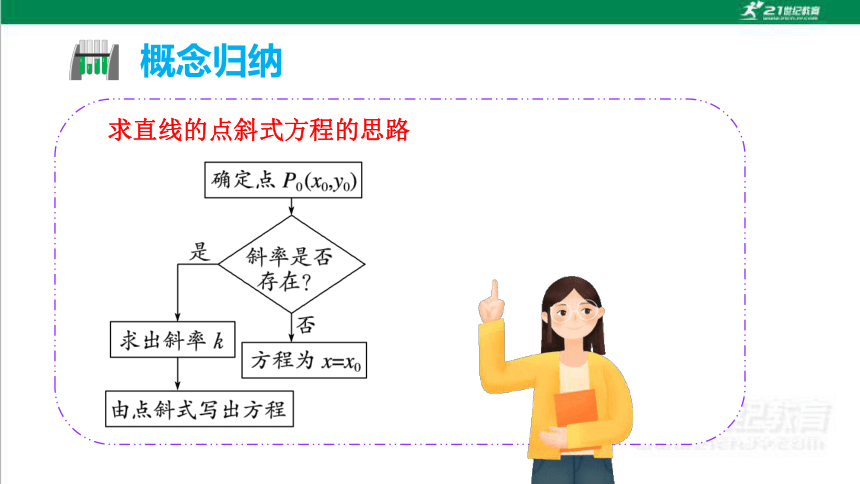
求直线的点斜式方程的思路
概念归纳
1.写出满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线y= 的倾斜角的2倍;
练一练
(2)经过点P(5,-2),且与y轴平行.
与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.
练一练
我们称方程______________为过点P0(x0,y0),斜率为k的直线l的方程.
由于该方程由直线上一定点及其斜率确定,因此把方程y-y0=k(x-x0)称为直线的___________,简称点斜式.
y-y0=k(x-x0)
点斜式方程
概念归纳
注意点:
(1)点斜式应用的前提是直线的斜率存在,若斜率不存在,则不能应用此式.
(2)当直线与x轴平行或重合时,方程可简写为y=y0.
特别地,x轴的方程是y=0;
当直线与y轴平行或重合时,不能应用点斜式方程.
此时可将方程写成x=x0.
特别地,y轴的方程是x=0.
2.直线的斜截式方程
新知探究
例1(课本例2)已知直线 l 的斜率为 k,与 y 轴的交点是P(0,b),求直线 l 的方程.
解:经过点P(0,b),斜率为 k 的直线的点斜式方程是
y-b= k (x-0),
整理得 y = k x + b. (2)
概念归纳
直线 l 与y轴的交点(0,b)的纵坐标称为直线 l 在y轴上的截距(纵截距).
方程(2)由直线 l 的斜率和它在y轴上的截距确定,
因此把方程(2)称为直线的斜截式方程,简称斜截式.
注:直线的纵截距,不是一个点,也不是距离,
而是直线与y轴交点的纵坐标.
观察方程y = k x + b,与我们初中学过的一次函数解析式相同.
从直线方程的角度来认识一次函数 y = k x + b,它的图象是一条直线,其中参数 k 是直线的斜率,常数 b 是直线在 y 轴上的截距.
如果数列{an}为等差数列,
那么 an=a1+(n-1)d = dn+(a1-d ),
所以数列{an}的图象是直线 y = dx+(a1-d )上一系列孤立的点,该直线的斜率为 d.
因为( n,an), ( m,am) 为直线上的两点,
所以 ,
所以 an= am + (n-m)d,(n,m∈N+) .
典例剖析
例2.根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
由直线方程的斜截式可知,
所求直线方程为y=2x+5.
(2)倾斜角为150°,在y轴上的截距是-2;
∵直线的倾斜角为150°,
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.
∵直线的倾斜角为60°,
∵直线与y轴的交点到原点的距离为3,
∴直线在y轴上的截距b=3或b=-3.
练一练
∴其倾斜角α=120°,
求直线的斜截式方程的策略
概念归纳
1.直线l与y轴的交点(0,b)的_______称为直线l在y轴上的截距.
2.把方程y=kx+b称为直线的斜截式方程,简称斜截式.
纵坐标
注意点:
(1)直线的斜截式方程是直线的点斜式方程的特殊情况;由直线的斜截式方程可直接得到直线的斜率和在y轴上的截距.
(2)截距是一个实数,它是直线与坐标轴交点的横坐标或纵坐标,可以为正数、负数和0.当直线过原点时,它在x轴上的截距和在y轴上的截距都为0.
3.含参数的直线方程的几何特征
新知探究
例3.已知直线l:y=ax+ .
(1)求证:无论a为何值,直线l必经过第一象限;
所以直线l必经过第一象限.
例3.已知直线l:y=ax+ .
(2)若直线l不经过第二象限,求实数a的取值范围.
若直线l不经过第二象限,
则直线l的斜率kl≥3,
即a≥3.
所以实数a的取值范围为[3,+∞).
典例剖析
对于含参数k的直线y-y0=k(x-x0),
该直线恒过定点(x0,y0).
概念归纳
2.(1)已知直线y=kx+1-3k,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
直线y=kx+1-3k变形为y-1=k(x-3),
由直线的点斜式可得直线恒过定点(3,1).
练一练
C
(2)直线y=ax- 的图象可能是( )
练一练
B
1.已知直线的方程是y+2=-x-1,则( )
A.直线经过定点(2,-1),斜率为-1
B.直线经过定点(1,-2),斜率为-1
C.直线经过定点(-2,-1),斜率为1
D.直线经过定点(-1,-2),斜率为-1
随堂练
D
B
随堂练
3.若直线y=kx+b经过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
B
C
错因分析
例4 一条直线l过点(2,1)且与x轴的夹角为45°,则这条直线方程为____________________.
y=x-1或y=-x+3
解析:∵直线l与x轴的夹角为45°,
∴直线l的倾斜角α=45°或135°.
∴直线l的斜率k=1或-1.
∴直线l的方程为:y-1=x-2或y-1=-(x-2)
即y=x-1或y=-x+3.
易错辨析 忽视倾斜角的范围出错
出错原因:
误认为夹角就是直线l的倾斜角,导致漏掉了倾斜角为135°的情形.
纠错心得:
在处理直线问题时,一定要注意倾斜角的取值范围,否则很容易会出现只考虑锐角而丢掉钝角的情况,而漏解.
错因分析
分层练习-基础
1.经过点P(0,2)且斜率为2的直线的方程为( )
A.y=-2x-2 B.y=2x-2
C.y=2x+2 D.y=-2x+2
2.已知一直线经过点A(3,-2),且与x轴平行,则该直线的方程为( )
A.x=3 B.x=-2
C.y=3 D.y=-2
C
D
分层练习-基础
3.若直线l的倾斜角为45°,且过点(0,-1),则直线l的方程是( )
A.y-1=x B.y+1=x
C.y-1=-x D.y+1=-x
4.(多选)给出下列四个结论,正确的是( )
A.方程k= 与方程y-2=k(x+1)可表示同一直线
B.若直线l过点P(x1,y1),倾斜角为90°,则其方程是x=x1
C.若直线l过点P(x1,y1),斜率为0,则其方程是y=y1
D.所有的直线都有点斜式和斜截式方程
B
BC
5.直线y-b=2(x-a)在y轴上的截距为( )
A.a+b B.2a-b
C.b-2a D.|2a-b|
分层练习-基础
C
BC
7.不管k为何值,直线y=k(x-2)+3必过定点_____.
(2,3)
8.在y轴上的截距为-6,且与y轴相交成30°角的直线的
斜截式方程是____________________________.
分层练习-基础
9.求倾斜角为直线y= +1的倾斜角的一半,且分别满足下列条件的直线方程.
(1)经过点(-4,1);
分层练习-基础
(2)在y轴上的截距为-10.
因为直线在y轴上的截距为-10,
分层练习-基础
10.直线l过点(2,2),且与x轴和直线y=x围成的三角形的面积为2,求直线l的方程.
分层练习-基础
当直线l的斜率不存在时,l的方程为x=2,经检验,符合题意;
当直线l的斜率存在时,设直线l的方程为y-2=k(x-2),易知k≠0,
11.(多选)直线(m2+2m)x+(2m2-m+3)y=4m+1在y轴上的截距为1,
则m的值可以是( )
分层练习-巩固
12.直线y=ax与直线y=x+a在同一直角坐标系中的图象可能是( )
CD
C
13.(多选)经过点(2,1),且与两坐标轴围成等腰直角三角形的直线方程
为( )
A.y=x+3 B.y=x-1
C.y=-x+3 D.y=-x-1
分层练习-巩固
14.将直线y= (x-2)绕点(2,0)按逆时针方向旋转60°后所得直线的
斜截式方程是________________.
BC
分层练习-拓展
15.已知点A(1,3),B(-2,-1).若直线l:y=k(x-2)+1与线段AB相交,
则k的取值范围是_________.
16.已知直线l:y=kx+2k+1.
(1)求证:直线l恒过一个定点;
由y=kx+2k+1,
得y-1=k(x+2).
由直线方程的点斜式可知,直线l恒过定点(-2,1).
分层练习-拓展
(2)若当-3设函数f(x)=kx+2k+1,显然其图象是一条直线(如图所示),
若使当-3课堂小结
1.知识清单:
(1)直线的点斜式方程.
(2)直线的斜截式方程.
(3)含参数的直线方程的几何特征.
2.方法归纳:待定系数法、数形结合法.
3.常见误区:求直线的方程时忽视斜率不存在的情况;
混淆截距与距离.
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.2.1 直线的点斜式方程
2.2 直线的方程
学习目标
1.了解由斜率公式推导直线的点斜式方程的过程.
2.掌握直线的点斜式方程与斜截式方程.(重点)
3.会利用直线的点斜式方程与斜截式方程解决有关的问题.(难点)
情景导入
旧知回顾
上节课我们学习了直线的倾斜角与斜率,你能简述一下它们的概念吗?
直线的倾斜角:
当直线 l 与 x 轴相交时,我们把 x 轴正向绕交点逆时针旋转到与直线 l 向上方向首次重合所成的角 α 叫作直线 l 的倾斜角.
倾斜角的取值范围: 0 ≤ α < π.
你能在纸上默写出斜率公式吗?
斜率公式:经过两个不同点
A(x1,y1),B (x2,y2),(x1≠x2)
的直线的斜率为
情景导入
射击手在进行射击训练时,要掌握两个动作要领:
一是托枪的手要非常稳,
二是眼睛要瞄准目标的方向.
若把子弹飞行的轨迹看作一条直线,
并且射击手达到上述的两个动作要求,
试分析子弹是否会击中目标.
给定直线的斜率和直线上一点,或者给定两点,都能唯一确定一条直线.
本节,我们将用给定的条件,将直线上所有点的坐标(x,y)满足的共同关系表示出来,这就是直线方程.
1.直线的点斜式方程
新知探究
如图 ,已知直线 l 的斜率为 k,且 l 过已知点 P0(x0, y0),
设 P(x, y)为 l 上不同于P0的任意一点.
因为直线 l 的斜率
于是可得 y -y0 = k (x-x0).(1)
可以验证,直线 l 上的每个点(包括点P0)的坐标都是这个方程的解;
反过来,以这个方程的解为坐标的点都在直线 l 上.
我们称方程(1)为过点 P0(x0, y0),斜率为 k 的直线 l 的方程.
由于该方程由直线上一定点及其斜率确定,因此把方程(1)称为直线的点斜式方程,简称点斜式.
当直线 l 与 x 轴垂直时,斜率不存在,其方程不能用点斜式表示,但因为 l 上每一点的横坐标都等于x0,所以它的方程是 x = x0 .
综上可知,若直线 l 过点 P0(x0, y0),
当直线 l 与 x 轴不垂直时,斜率为 k,
那么直线 l 的方程为:y -y0 = k (x-x0).
特别地,当直线 l 与 x 轴平行或重合时,斜率 k=0,
直线 l 的方程为:y = y0 .
当直线 l 与 x 轴垂直时,斜率不存在,
直线 l 的方程为:x = x0 .
课本例1 已知直线l经过点P(2,3),斜率为2,求直线l的方程,并画出该直线.
经过点P(2,3),斜率为2的直线的点斜式方程是
y-3=2(x-2).
画该直线时,可在直线l上另取一点P1(x1,y1),
如取x1=1,y1=1,得P1(1,1),
过P,P1作直线即为所求,如右图.
课本例题
例 1 根据条件写出下列直线的点斜式方程:
(1)经过点A(-4,3),斜率k=3;
由点斜式方程可知,所求直线的点斜式方程为y-3=3(x+4).
典例剖析
(2)经过点B(-1,4),倾斜角为135°.
由题意知,直线的斜率k=tan 135°=-1,
故所求直线的点斜式方程为y-4=-(x+1).
求直线的点斜式方程的思路
概念归纳
1.写出满足下列条件的直线方程:
(1)经过点(2,-3),倾斜角是直线y= 的倾斜角的2倍;
练一练
(2)经过点P(5,-2),且与y轴平行.
与y轴平行的直线,其斜率k不存在,不能用点斜式方程表示.
但直线上点的横坐标均为5,
故直线方程可记为x=5.
练一练
我们称方程______________为过点P0(x0,y0),斜率为k的直线l的方程.
由于该方程由直线上一定点及其斜率确定,因此把方程y-y0=k(x-x0)称为直线的___________,简称点斜式.
y-y0=k(x-x0)
点斜式方程
概念归纳
注意点:
(1)点斜式应用的前提是直线的斜率存在,若斜率不存在,则不能应用此式.
(2)当直线与x轴平行或重合时,方程可简写为y=y0.
特别地,x轴的方程是y=0;
当直线与y轴平行或重合时,不能应用点斜式方程.
此时可将方程写成x=x0.
特别地,y轴的方程是x=0.
2.直线的斜截式方程
新知探究
例1(课本例2)已知直线 l 的斜率为 k,与 y 轴的交点是P(0,b),求直线 l 的方程.
解:经过点P(0,b),斜率为 k 的直线的点斜式方程是
y-b= k (x-0),
整理得 y = k x + b. (2)
概念归纳
直线 l 与y轴的交点(0,b)的纵坐标称为直线 l 在y轴上的截距(纵截距).
方程(2)由直线 l 的斜率和它在y轴上的截距确定,
因此把方程(2)称为直线的斜截式方程,简称斜截式.
注:直线的纵截距,不是一个点,也不是距离,
而是直线与y轴交点的纵坐标.
观察方程y = k x + b,与我们初中学过的一次函数解析式相同.
从直线方程的角度来认识一次函数 y = k x + b,它的图象是一条直线,其中参数 k 是直线的斜率,常数 b 是直线在 y 轴上的截距.
如果数列{an}为等差数列,
那么 an=a1+(n-1)d = dn+(a1-d ),
所以数列{an}的图象是直线 y = dx+(a1-d )上一系列孤立的点,该直线的斜率为 d.
因为( n,an), ( m,am) 为直线上的两点,
所以 ,
所以 an= am + (n-m)d,(n,m∈N+) .
典例剖析
例2.根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
由直线方程的斜截式可知,
所求直线方程为y=2x+5.
(2)倾斜角为150°,在y轴上的截距是-2;
∵直线的倾斜角为150°,
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.
∵直线的倾斜角为60°,
∵直线与y轴的交点到原点的距离为3,
∴直线在y轴上的截距b=3或b=-3.
练一练
∴其倾斜角α=120°,
求直线的斜截式方程的策略
概念归纳
1.直线l与y轴的交点(0,b)的_______称为直线l在y轴上的截距.
2.把方程y=kx+b称为直线的斜截式方程,简称斜截式.
纵坐标
注意点:
(1)直线的斜截式方程是直线的点斜式方程的特殊情况;由直线的斜截式方程可直接得到直线的斜率和在y轴上的截距.
(2)截距是一个实数,它是直线与坐标轴交点的横坐标或纵坐标,可以为正数、负数和0.当直线过原点时,它在x轴上的截距和在y轴上的截距都为0.
3.含参数的直线方程的几何特征
新知探究
例3.已知直线l:y=ax+ .
(1)求证:无论a为何值,直线l必经过第一象限;
所以直线l必经过第一象限.
例3.已知直线l:y=ax+ .
(2)若直线l不经过第二象限,求实数a的取值范围.
若直线l不经过第二象限,
则直线l的斜率kl≥3,
即a≥3.
所以实数a的取值范围为[3,+∞).
典例剖析
对于含参数k的直线y-y0=k(x-x0),
该直线恒过定点(x0,y0).
概念归纳
2.(1)已知直线y=kx+1-3k,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
直线y=kx+1-3k变形为y-1=k(x-3),
由直线的点斜式可得直线恒过定点(3,1).
练一练
C
(2)直线y=ax- 的图象可能是( )
练一练
B
1.已知直线的方程是y+2=-x-1,则( )
A.直线经过定点(2,-1),斜率为-1
B.直线经过定点(1,-2),斜率为-1
C.直线经过定点(-2,-1),斜率为1
D.直线经过定点(-1,-2),斜率为-1
随堂练
D
B
随堂练
3.若直线y=kx+b经过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
B
C
错因分析
例4 一条直线l过点(2,1)且与x轴的夹角为45°,则这条直线方程为____________________.
y=x-1或y=-x+3
解析:∵直线l与x轴的夹角为45°,
∴直线l的倾斜角α=45°或135°.
∴直线l的斜率k=1或-1.
∴直线l的方程为:y-1=x-2或y-1=-(x-2)
即y=x-1或y=-x+3.
易错辨析 忽视倾斜角的范围出错
出错原因:
误认为夹角就是直线l的倾斜角,导致漏掉了倾斜角为135°的情形.
纠错心得:
在处理直线问题时,一定要注意倾斜角的取值范围,否则很容易会出现只考虑锐角而丢掉钝角的情况,而漏解.
错因分析
分层练习-基础
1.经过点P(0,2)且斜率为2的直线的方程为( )
A.y=-2x-2 B.y=2x-2
C.y=2x+2 D.y=-2x+2
2.已知一直线经过点A(3,-2),且与x轴平行,则该直线的方程为( )
A.x=3 B.x=-2
C.y=3 D.y=-2
C
D
分层练习-基础
3.若直线l的倾斜角为45°,且过点(0,-1),则直线l的方程是( )
A.y-1=x B.y+1=x
C.y-1=-x D.y+1=-x
4.(多选)给出下列四个结论,正确的是( )
A.方程k= 与方程y-2=k(x+1)可表示同一直线
B.若直线l过点P(x1,y1),倾斜角为90°,则其方程是x=x1
C.若直线l过点P(x1,y1),斜率为0,则其方程是y=y1
D.所有的直线都有点斜式和斜截式方程
B
BC
5.直线y-b=2(x-a)在y轴上的截距为( )
A.a+b B.2a-b
C.b-2a D.|2a-b|
分层练习-基础
C
BC
7.不管k为何值,直线y=k(x-2)+3必过定点_____.
(2,3)
8.在y轴上的截距为-6,且与y轴相交成30°角的直线的
斜截式方程是____________________________.
分层练习-基础
9.求倾斜角为直线y= +1的倾斜角的一半,且分别满足下列条件的直线方程.
(1)经过点(-4,1);
分层练习-基础
(2)在y轴上的截距为-10.
因为直线在y轴上的截距为-10,
分层练习-基础
10.直线l过点(2,2),且与x轴和直线y=x围成的三角形的面积为2,求直线l的方程.
分层练习-基础
当直线l的斜率不存在时,l的方程为x=2,经检验,符合题意;
当直线l的斜率存在时,设直线l的方程为y-2=k(x-2),易知k≠0,
11.(多选)直线(m2+2m)x+(2m2-m+3)y=4m+1在y轴上的截距为1,
则m的值可以是( )
分层练习-巩固
12.直线y=ax与直线y=x+a在同一直角坐标系中的图象可能是( )
CD
C
13.(多选)经过点(2,1),且与两坐标轴围成等腰直角三角形的直线方程
为( )
A.y=x+3 B.y=x-1
C.y=-x+3 D.y=-x-1
分层练习-巩固
14.将直线y= (x-2)绕点(2,0)按逆时针方向旋转60°后所得直线的
斜截式方程是________________.
BC
分层练习-拓展
15.已知点A(1,3),B(-2,-1).若直线l:y=k(x-2)+1与线段AB相交,
则k的取值范围是_________.
16.已知直线l:y=kx+2k+1.
(1)求证:直线l恒过一个定点;
由y=kx+2k+1,
得y-1=k(x+2).
由直线方程的点斜式可知,直线l恒过定点(-2,1).
分层练习-拓展
(2)若当-3
若使当-3
1.知识清单:
(1)直线的点斜式方程.
(2)直线的斜截式方程.
(3)含参数的直线方程的几何特征.
2.方法归纳:待定系数法、数形结合法.
3.常见误区:求直线的方程时忽视斜率不存在的情况;
混淆截距与距离.
同课章节目录
