湘教版高中数学选择性必修第一册第2章平面解析几何初步2.3.1两条直线平行与垂直的判定课件(共49张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第2章平面解析几何初步2.3.1两条直线平行与垂直的判定课件(共49张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:46:08 | ||
图片预览











文档简介
(共49张PPT)
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.3.1 两条直线平行与垂直的判定
学习目标
1.根据直线的斜率来判定两条不重合直线的平行与垂直(重点)
2.会利用垂直与平行的关系求直线的方程(重点、难点)
3.根据直线的方向向量、法向量来判定两条不重合直线的平行与垂直(重点)
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱
子之间还有一些小的钢筋连接,这些钢筋有的互
相平行,你能感受到过山车中的平行吗?两条直
线的平行用什么来刻画呢?
情景导入
设在xOy平面上的两条直线l1,l2的斜率分别为k1,k2,它们的方程分别是 y=k1x+b1和 y=k2x+b2.
平面几何中讲到,两直线与第三条直线相交,则这两条直线平行的充分必要条件是同位角相等.
设两条直线的倾斜角分别为α1,α2.
新知探究
首先,我们来研究两条直线平行(不重合)的情形.
如果l1//l2,则α1=α2,从而 tanα1=tanα2,即k1=k2=k.
此时,两条直线的方程分别为 y=k1x+b1, y=k2x+b2,并且b1≠b2.
反之,若k1=k2,并且b1≠b2,则l1//l2.
由此得到
显然,根据上述结论,可以得到∶
若k1=k2,并且b1=b2,那么两条直线重合.
l1//l2 k1=k2 且 b1≠b2.
如果两条直线斜率都不存在,它们都与 x 轴垂直但在 x 轴上的截距不同,则这两条直线平行,如图.
如果两条直线斜率都不存在,它们都与 x 轴垂直且在 x 轴上的截距相同,则这两条直线重合.
当l1,l2斜率都存在时, k1=k2 且 b1≠b2.
当l1,l2斜率都不存在时, 横截距不相等.
综上可得:
l1//l2
例1 已知直线l1:3x+2y-6=0,l2:6x+4y-10=0.试判断直线l1与l2是
否平行.
课本例题
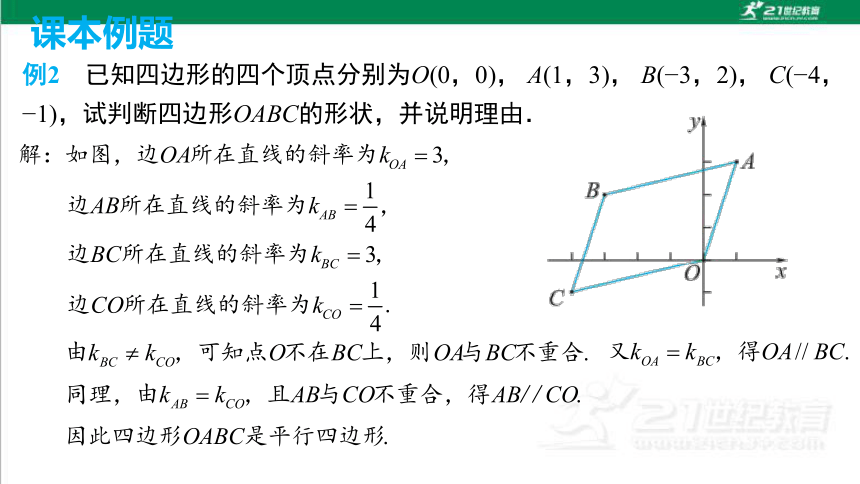
例2 已知四边形的四个顶点分别为O(0,0), A(1,3), B( 3,2), C( 4, 1),试判断四边形OABC的形状,并说明理由.
课本例题
除平行外,生活中也存在很多垂直关系,比如十字路口,黑板相邻两边等等,上节课我们学习了两条直线平行的判定
方法,研究了两条平行直线的倾斜角之间的关
系,当斜率存在时,斜率也有联系,那么两条
垂直直线的倾斜角和斜率是否也有关系呢?
情景导入
设在xOy平面上的两条直线l1,l2的倾斜角分别为α1,α2,它们的斜率
分别为k1,k2.
因此,当两直线的斜率都存在时,可得到
新知探究
如果两条直线l1,l2中的一条斜率不存在,另一条的斜率为零,(即一条垂直于 x 轴,垂直于 y 轴)那么这两条直线也垂直.
当l1,l2斜率都存在时,k1 k2 = -1.
当l1,l2中有一条斜率不存在时,另一条的斜率为零.
综上可得:
l1⊥l2
例3 如图,已知平面直角坐标系中三点A(4,3),B(2,1),C(5, 2).
证明:△ABC是直角三角形.
证明:由条件可知,
因为kAB kBC=-1,
所以AB⊥BC,即△ABC是直角三角形.
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距b2 =1.
(1)重合
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距b2 =1.
(2)平行
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距为b2 =1.
(3)垂直
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
(3)垂直
(1)重合
(2)平行
课本例题
我们知道斜率、方向向量、法向量都是刻画直线方向的几何要素,前面我们是根据斜率来判定两条直线平行,事实上也可以借助直线的方向向量或法向量来判定.
已知两条直线的一般方程分别为l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
则两条直线的法向量分别为 n1= (A1,B1),n2 = (A2,B2).
判断两条直线平行
l1//l2
法向量平行且两直线不重合
A1= λ A2,B1= λB2,C1≠λC2.
确保两直线不重合
新知探究
我们知道斜率、方向向量、法向量都是刻画直线方向的几何要素,前面我们是根据斜率来判定两条直线平行,事实上也可以借助直线的方向向量或法向量来判定.
已知两条直线的一般方程分别为l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
则两条直线的法向量分别为 n1= (A1,B1),n2 = (A2,B2).
判断两条直线垂直
l1⊥l2
法向量垂直
(A1,B1) (A2,B2) = A1A2+B1B2 = 0.
l1⊥l2 方向向量垂直 (1,k1) (1,k2) =1+k1 k2= 0 k1 k2=-1.
例5 求过点(-3,4),且与直线l:3x-4y+29=0平行的直线.
课本例题
例5 求过点(-3,4),且与直线l:3x-4y+29=0平行的直线.
解:设所求直线的方程为3x-4y+C =0 (C ≠ 29).
因为过点(-3,4),
所以 3×(-3)-4×4+C =0,
解得C = 25.
因此,所求直线的方程为3x-4y+25 =0 .
与Ax+By+C=0平行的直线方程可设为Ax+By+C′ =0(C′ ≠ C).
课本例题
例5变式 求过点(-3,4),且与直线l:3x-4y+29=0垂直的直线.
求斜率后可用点斜式
例5变式 求过点(-3,4),且与直线l:3x-4y+29=0垂直的直线.
解:设所求直线的方程为4x+3y+C =0.
因为过点(-3,4),
所以 4×(-3)+3×4+C =0,
解得C = 0.
因此,所求直线的方程为4x+3y =0 .
与Ax+By+C=0垂直的直线方程可设为Bx-Ay+C′ =0.
例3 已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),P(-1,a-2),若l1⊥l2,则a的值为________.
易错辨析 忽视直线斜率不存在的情况致错
错因分析
0或5
本题容易由k1·k2=-1得a=0而出错,误认为直线l1的斜率存在.
已知点的坐标中有参数的,首先判断直线的斜率是否存在,本题中直线l1的斜率就要分存在与不存在两种情况解答.
错因分析
题型1 两条直线平行的判定与应用
典例剖析
典例剖析
典例剖析
看斜率
相等?
提醒:若已知直线上点的坐标,判断直线是否平行时,要考虑直线重合的情况.
平行
平行
不平行
都不存在
是
否
归纳总结
(1)l1经过点A(3,2),B(3,-1),l2经过点M(1,1),N(2,1),
判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),
直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
题型2 两条直线垂直的判定与应用
典例剖析
典例剖析
典例剖析
使用斜率公式判定两直线垂直的步骤
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式对参数进行讨论.
提醒:若已知点的坐标含有参数,利用两条直线的垂直关系求参数值时,要注意讨论斜率是否存在.
归纳总结
如图,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5 m,宽AB=3 m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
典例剖析
题型3 平行与垂直的综合应用
典例剖析
利用坐标法解决实际问题的三个步骤
(1)建立恰当的直角坐标系.
(2)将“形”转化为“数”进行运算.
(3)将计算结果转化为实际问题所求解的问题.
提醒:利用平行、垂直关系式的关键在于正确求解斜率,特别是含参数的问题,必须要分类讨论;其次要注意的是斜率不存在并不意味着问题无解.
归纳总结
已知直线l1经过A(3,m),B(m-1,2),
直线l2经过点C(1,2),D(-2,m+2).
(1)若l1∥l2,求m的值;
(2)若l1⊥l2,求m的值.
题型四 由两条直线平行、垂直的条件求参数的值
典例剖析
1.两条直线平行时关注是否重合
由于斜率相等的两条直线可能平行,也可能重合,所以由两条直线平行得斜率相等,求参数的值后要注意检验,如本题中m=1或m=6时,经检验l1与l2不重合.
归纳总结
归纳总结
1.若直线l1的倾斜角为135°,直线l2经过点P(-2,-1),Q(3,-6),则直线l1与l2的位置关系是( )
A.垂直 B.平行
C.重合 D.平行或重合
D
分层练习-基础
C
分层练习-基础
A
B
分层练习-基础
5.已知△ABC中,A(0,3),B(2,-1),E,F分别为AC,BC的中点,则直线EF的斜率为________.
7.若A(-4,2),B(6,-4),C(12,6),D(2,12),则下面四个结论:
①AB∥CD;②AB⊥AD;③AC∥BD;④AC⊥BD.其中正确的序号有________.
-2
±2
①②④
分层练习-基础
8.已知A(1,5),B(-1,1),C(3,2),若四边形ABCD是平行四边形,求D点的坐标.
分层练习-基础
9.已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点);
(2)∠MPN是直角.
分层练习-基础
分层练习-巩固
10.满足下列条件的直线l1与l2,其中l1∥l2的是( )
①l1的斜率为2,l2过点A(1,2),B(4,8),且l1不经过A点;
②l1经过点P(3,3),Q(-5,3),l2平行于x轴,但不经过P点;
③l1经过点M(-1,0),N(-5,-2),l2经过点R(-4,3),S(0,5).
A.①② B.②③ C.①③ D.①②③
11.(多选)已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与CD平行,则m的值为( )
A.-1 B.0
C.1 D.2
D
BC
分层练习-拓展
12.如图,在平面直角坐标系Oxy中,设△ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)为线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F.若BE⊥AC,求证:CF⊥AB.
分层练习-拓展
课堂小结
两直线平行于垂直的判定
平行
垂直
斜率相等
斜率都不存在
斜率之积等于-1
一条直线斜率为0,另一条斜率不存在
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.3.1 两条直线平行与垂直的判定
学习目标
1.根据直线的斜率来判定两条不重合直线的平行与垂直(重点)
2.会利用垂直与平行的关系求直线的方程(重点、难点)
3.根据直线的方向向量、法向量来判定两条不重合直线的平行与垂直(重点)
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱
子之间还有一些小的钢筋连接,这些钢筋有的互
相平行,你能感受到过山车中的平行吗?两条直
线的平行用什么来刻画呢?
情景导入
设在xOy平面上的两条直线l1,l2的斜率分别为k1,k2,它们的方程分别是 y=k1x+b1和 y=k2x+b2.
平面几何中讲到,两直线与第三条直线相交,则这两条直线平行的充分必要条件是同位角相等.
设两条直线的倾斜角分别为α1,α2.
新知探究
首先,我们来研究两条直线平行(不重合)的情形.
如果l1//l2,则α1=α2,从而 tanα1=tanα2,即k1=k2=k.
此时,两条直线的方程分别为 y=k1x+b1, y=k2x+b2,并且b1≠b2.
反之,若k1=k2,并且b1≠b2,则l1//l2.
由此得到
显然,根据上述结论,可以得到∶
若k1=k2,并且b1=b2,那么两条直线重合.
l1//l2 k1=k2 且 b1≠b2.
如果两条直线斜率都不存在,它们都与 x 轴垂直但在 x 轴上的截距不同,则这两条直线平行,如图.
如果两条直线斜率都不存在,它们都与 x 轴垂直且在 x 轴上的截距相同,则这两条直线重合.
当l1,l2斜率都存在时, k1=k2 且 b1≠b2.
当l1,l2斜率都不存在时, 横截距不相等.
综上可得:
l1//l2
例1 已知直线l1:3x+2y-6=0,l2:6x+4y-10=0.试判断直线l1与l2是
否平行.
课本例题
例2 已知四边形的四个顶点分别为O(0,0), A(1,3), B( 3,2), C( 4, 1),试判断四边形OABC的形状,并说明理由.
课本例题
除平行外,生活中也存在很多垂直关系,比如十字路口,黑板相邻两边等等,上节课我们学习了两条直线平行的判定
方法,研究了两条平行直线的倾斜角之间的关
系,当斜率存在时,斜率也有联系,那么两条
垂直直线的倾斜角和斜率是否也有关系呢?
情景导入
设在xOy平面上的两条直线l1,l2的倾斜角分别为α1,α2,它们的斜率
分别为k1,k2.
因此,当两直线的斜率都存在时,可得到
新知探究
如果两条直线l1,l2中的一条斜率不存在,另一条的斜率为零,(即一条垂直于 x 轴,垂直于 y 轴)那么这两条直线也垂直.
当l1,l2斜率都存在时,k1 k2 = -1.
当l1,l2中有一条斜率不存在时,另一条的斜率为零.
综上可得:
l1⊥l2
例3 如图,已知平面直角坐标系中三点A(4,3),B(2,1),C(5, 2).
证明:△ABC是直角三角形.
证明:由条件可知,
因为kAB kBC=-1,
所以AB⊥BC,即△ABC是直角三角形.
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距b2 =1.
(1)重合
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距b2 =1.
(2)平行
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
解:直线l1,l2的方程可以分别化为
因此直线l1的斜率 在y轴上的截距
直线l2的斜率k2 =-λ,在y轴上的截距为b2 =1.
(3)垂直
课本例题
例4 已知 λ ≠-1,求 λ 取何值时,直线l1:2x+(λ+1)y=2, l2:λx+y=1:
(1)重合; (2)平行; (3)垂直.
(3)垂直
(1)重合
(2)平行
课本例题
我们知道斜率、方向向量、法向量都是刻画直线方向的几何要素,前面我们是根据斜率来判定两条直线平行,事实上也可以借助直线的方向向量或法向量来判定.
已知两条直线的一般方程分别为l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
则两条直线的法向量分别为 n1= (A1,B1),n2 = (A2,B2).
判断两条直线平行
l1//l2
法向量平行且两直线不重合
A1= λ A2,B1= λB2,C1≠λC2.
确保两直线不重合
新知探究
我们知道斜率、方向向量、法向量都是刻画直线方向的几何要素,前面我们是根据斜率来判定两条直线平行,事实上也可以借助直线的方向向量或法向量来判定.
已知两条直线的一般方程分别为l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,
则两条直线的法向量分别为 n1= (A1,B1),n2 = (A2,B2).
判断两条直线垂直
l1⊥l2
法向量垂直
(A1,B1) (A2,B2) = A1A2+B1B2 = 0.
l1⊥l2 方向向量垂直 (1,k1) (1,k2) =1+k1 k2= 0 k1 k2=-1.
例5 求过点(-3,4),且与直线l:3x-4y+29=0平行的直线.
课本例题
例5 求过点(-3,4),且与直线l:3x-4y+29=0平行的直线.
解:设所求直线的方程为3x-4y+C =0 (C ≠ 29).
因为过点(-3,4),
所以 3×(-3)-4×4+C =0,
解得C = 25.
因此,所求直线的方程为3x-4y+25 =0 .
与Ax+By+C=0平行的直线方程可设为Ax+By+C′ =0(C′ ≠ C).
课本例题
例5变式 求过点(-3,4),且与直线l:3x-4y+29=0垂直的直线.
求斜率后可用点斜式
例5变式 求过点(-3,4),且与直线l:3x-4y+29=0垂直的直线.
解:设所求直线的方程为4x+3y+C =0.
因为过点(-3,4),
所以 4×(-3)+3×4+C =0,
解得C = 0.
因此,所求直线的方程为4x+3y =0 .
与Ax+By+C=0垂直的直线方程可设为Bx-Ay+C′ =0.
例3 已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),P(-1,a-2),若l1⊥l2,则a的值为________.
易错辨析 忽视直线斜率不存在的情况致错
错因分析
0或5
本题容易由k1·k2=-1得a=0而出错,误认为直线l1的斜率存在.
已知点的坐标中有参数的,首先判断直线的斜率是否存在,本题中直线l1的斜率就要分存在与不存在两种情况解答.
错因分析
题型1 两条直线平行的判定与应用
典例剖析
典例剖析
典例剖析
看斜率
相等?
提醒:若已知直线上点的坐标,判断直线是否平行时,要考虑直线重合的情况.
平行
平行
不平行
都不存在
是
否
归纳总结
(1)l1经过点A(3,2),B(3,-1),l2经过点M(1,1),N(2,1),
判断l1与l2是否垂直;
(2)已知直线l1经过点A(3,a),B(a-2,3),
直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
题型2 两条直线垂直的判定与应用
典例剖析
典例剖析
典例剖析
使用斜率公式判定两直线垂直的步骤
(1)一看:就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步.
(2)二代:就是将点的坐标代入斜率公式.
(3)三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式对参数进行讨论.
提醒:若已知点的坐标含有参数,利用两条直线的垂直关系求参数值时,要注意讨论斜率是否存在.
归纳总结
如图,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5 m,宽AB=3 m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
典例剖析
题型3 平行与垂直的综合应用
典例剖析
利用坐标法解决实际问题的三个步骤
(1)建立恰当的直角坐标系.
(2)将“形”转化为“数”进行运算.
(3)将计算结果转化为实际问题所求解的问题.
提醒:利用平行、垂直关系式的关键在于正确求解斜率,特别是含参数的问题,必须要分类讨论;其次要注意的是斜率不存在并不意味着问题无解.
归纳总结
已知直线l1经过A(3,m),B(m-1,2),
直线l2经过点C(1,2),D(-2,m+2).
(1)若l1∥l2,求m的值;
(2)若l1⊥l2,求m的值.
题型四 由两条直线平行、垂直的条件求参数的值
典例剖析
1.两条直线平行时关注是否重合
由于斜率相等的两条直线可能平行,也可能重合,所以由两条直线平行得斜率相等,求参数的值后要注意检验,如本题中m=1或m=6时,经检验l1与l2不重合.
归纳总结
归纳总结
1.若直线l1的倾斜角为135°,直线l2经过点P(-2,-1),Q(3,-6),则直线l1与l2的位置关系是( )
A.垂直 B.平行
C.重合 D.平行或重合
D
分层练习-基础
C
分层练习-基础
A
B
分层练习-基础
5.已知△ABC中,A(0,3),B(2,-1),E,F分别为AC,BC的中点,则直线EF的斜率为________.
7.若A(-4,2),B(6,-4),C(12,6),D(2,12),则下面四个结论:
①AB∥CD;②AB⊥AD;③AC∥BD;④AC⊥BD.其中正确的序号有________.
-2
±2
①②④
分层练习-基础
8.已知A(1,5),B(-1,1),C(3,2),若四边形ABCD是平行四边形,求D点的坐标.
分层练习-基础
9.已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点);
(2)∠MPN是直角.
分层练习-基础
分层练习-巩固
10.满足下列条件的直线l1与l2,其中l1∥l2的是( )
①l1的斜率为2,l2过点A(1,2),B(4,8),且l1不经过A点;
②l1经过点P(3,3),Q(-5,3),l2平行于x轴,但不经过P点;
③l1经过点M(-1,0),N(-5,-2),l2经过点R(-4,3),S(0,5).
A.①② B.②③ C.①③ D.①②③
11.(多选)已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与CD平行,则m的值为( )
A.-1 B.0
C.1 D.2
D
BC
分层练习-拓展
12.如图,在平面直角坐标系Oxy中,设△ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)为线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F.若BE⊥AC,求证:CF⊥AB.
分层练习-拓展
课堂小结
两直线平行于垂直的判定
平行
垂直
斜率相等
斜率都不存在
斜率之积等于-1
一条直线斜率为0,另一条斜率不存在
同课章节目录
