湘教版高中数学选择性必修第一册第2章平面解析几何初步2.5.1圆的标准方程课件(共30张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第2章平面解析几何初步2.5.1圆的标准方程课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:47:04 | ||
图片预览











文档简介
(共30张PPT)
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.5.1 圆的标准方程
学习目标
1.掌握圆的标准方程,理解圆的标准方程及其推导过程(重点)
2.能够根据圆的标准方程正确地写出其圆心和半径(重点)
3.掌握圆的标准方程的特点,能根据已知条件求出圆的标准方程(难点)
《古朗月行》
唐 李白
小时不识月,呼作白玉盘.
又疑瑶台镜,飞在青云端.
月亮,是中国人心目中的宇宙精灵,古代的人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写,如果把天空看作一个平面,月亮当作一个圆,建立一个平面直角坐标系,那么圆的直角坐标方程如何表示?
《墨子·经上》云:“圆,一中同长也.”这句朴素的定义用数学语言来描述就是:圆是平面内到一定点的距离等于定长的所有的点组成的集合,这个定点即圆心,而定长就是半径,只要给定了圆心和半径,这个圆就确定了.
情景导入
用“坐标法”解决有关几何问题的基本步骤:
第一步;建立坐标系,用坐标系表示有关的量;
第二步:进行有关代数运算;
第三步:把代数运算结果“翻译”成几何关系.
代数
几何
几何
在初中,我们用几何方法研究了圆的几何性质. 现在,我们在平面直角坐标系中建立圆的方程,用代数方法进一步研究圆的性质.
情景导入
这就得到了圆心为C(a,b),半径为r的圆的方程:
在平面直角坐标系中,圆心为C(a,b),半径为 r 的圆的方程,也就是求圆上任意一点P的坐标(x,y)满足的条件.
它叫作圆的标准方程.
特别地,圆心在原点(0,0),
半径为 r 的圆的方程为:
x2+y2= r2.
新知探究
例1 求以C(3,5)为圆心且经过原点O的圆的方程.
课本例题
例2 已知某圆经过A(-2,2),B(6,0)两点,圆心M在直线2x-y=1上,
求该圆的方程.
待定系数法是求曲线方程常用的一种方法.
课本例题
例2 已知某圆经过A(-2,2),B(6,0)两点,圆心M在直线2x-y=1上,
求该圆的方程.
课本例题
已知某圆圆心C在x轴上,半径为10,且在y轴上截得的线段AB的长为16,则圆的标准方程为________.
易错警示 求圆的标准方程
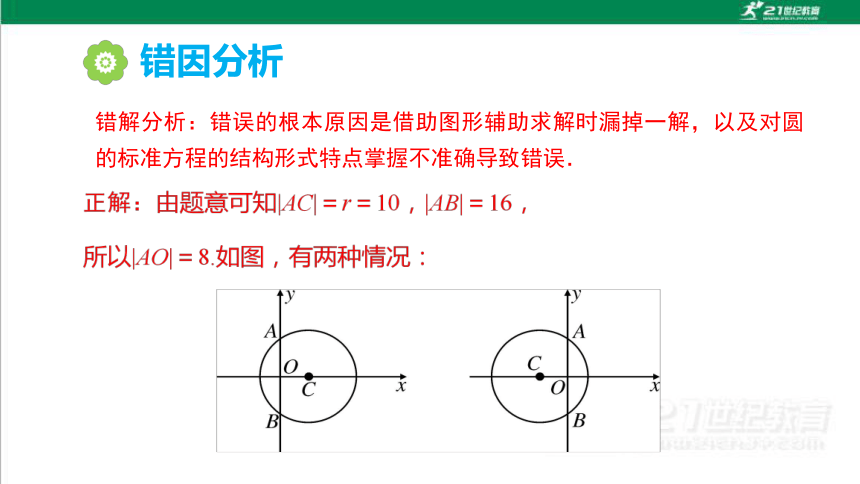
错因分析
(x+6)2+y2=100
错解分析:错误的根本原因是借助图形辅助求解时漏掉一解,以及对圆的标准方程的结构形式特点掌握不准确导致错误.
错因分析
错因分析
防范措施:
1.突出图形的作用
图形可以帮助我们直观地分析题意,能有效地避免漏解,提高解题的准确性.如本题通过图形能准确地判定出圆心在y轴左右两侧这两种情形,忽略此点易造成漏解.
2.准确认识圆的标准方程的结构特点
圆的标准方程的结构特点是:等号左边是平方和的形式,右边是半径的平方而非半径.
如本题中若不注意此点则易出现类似(x±6)2+y2=10的失误.
错因分析
题型1 用直接法求圆的标准方程
典例剖析
用直接法求圆的标准方程的策略
(1)首先求出圆心坐标和半径,然后直接写出圆的标准方程.
(2)确定圆心和半径时,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“过切点与切线垂直的直线必过圆心”等.
提醒:当圆与坐标轴相切时要特别注意圆心的坐标与圆的半径的关系.
归纳总结
经过点A(-1,3),B(4,2)且圆心在x轴上的圆的方程是________________.
典例剖析
题型2 用待定系数法求圆的标准方程
(x-1)2+y2=13
1.待定系数法求圆的标准方程的一般步骤
设方程
列方程组
解方程组
得方程
设所求圆的方程为(x-a)2+(y-b)2=r2
由已知条件,建立关于a,b,r
解方程组,求出a,b,r
将a,b,r代入所设方程,得所求原方程
如图,已知两点P1(4,9)和P2(6,3).
(1)求以P1P2为直径的圆的方程;
(2)试判断点M(6,9),N(3,3),Q(5,3)是在圆上、在圆内、还是在圆外.
题型3 点与圆的位置关系
典例剖析
归纳总结
判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:主要是把点的坐标代入圆的标准方程来判断:
点P(x0,y0)在圆C上 (x0-a)2+(y0-b)2=r2;
点P(x0,y0)在圆C内 (x0-a)2+(y0-b)2点P(x0,y0)在圆C外 (x0-a)2+(y0-b)2>r2.
分层练习-基础
1.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y-2)2=25 B.(x+1)2+(y+2)2=25
C.(x+1)2+(y+2)2=100 D.(x-1)2+(y-2)2=100
A
D
分层练习-基础
3.点P(m,5)与圆x2+y2=24的位置关系是( )
A.在圆外 B.在圆内
C.在圆上 D.不确定
A
A
分层练习-基础
5.一圆与圆C:(x+2)2+(y+1)2=3为同心圆且面积为圆C面积的两倍,此圆的标准方程为 .
8.过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=________.
(x+2)2+(y+1)2=6
(x+1)2+y2=2
或(x+3)2+y2=2
(x-2)2+y2=9
分层练习-巩固
9.已知A(0,1),B(2,1),C(3,4),D(-1,2),问这四点能否在同一个圆上?为什么?
分层练习-巩固
11.已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
分层练习-巩固
12.如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
分层练习-拓展
12.如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
分层练习-巩固
圆的标准方程:
圆心为C(a,b),半径为r的圆的方程:
点与圆的位置关系的判断:
课堂小结
圆上的点到定点的最值:
湘教版2019高一数学(选修一) 第二章 平面解析几何初步
2.5.1 圆的标准方程
学习目标
1.掌握圆的标准方程,理解圆的标准方程及其推导过程(重点)
2.能够根据圆的标准方程正确地写出其圆心和半径(重点)
3.掌握圆的标准方程的特点,能根据已知条件求出圆的标准方程(难点)
《古朗月行》
唐 李白
小时不识月,呼作白玉盘.
又疑瑶台镜,飞在青云端.
月亮,是中国人心目中的宇宙精灵,古代的人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写,如果把天空看作一个平面,月亮当作一个圆,建立一个平面直角坐标系,那么圆的直角坐标方程如何表示?
《墨子·经上》云:“圆,一中同长也.”这句朴素的定义用数学语言来描述就是:圆是平面内到一定点的距离等于定长的所有的点组成的集合,这个定点即圆心,而定长就是半径,只要给定了圆心和半径,这个圆就确定了.
情景导入
用“坐标法”解决有关几何问题的基本步骤:
第一步;建立坐标系,用坐标系表示有关的量;
第二步:进行有关代数运算;
第三步:把代数运算结果“翻译”成几何关系.
代数
几何
几何
在初中,我们用几何方法研究了圆的几何性质. 现在,我们在平面直角坐标系中建立圆的方程,用代数方法进一步研究圆的性质.
情景导入
这就得到了圆心为C(a,b),半径为r的圆的方程:
在平面直角坐标系中,圆心为C(a,b),半径为 r 的圆的方程,也就是求圆上任意一点P的坐标(x,y)满足的条件.
它叫作圆的标准方程.
特别地,圆心在原点(0,0),
半径为 r 的圆的方程为:
x2+y2= r2.
新知探究
例1 求以C(3,5)为圆心且经过原点O的圆的方程.
课本例题
例2 已知某圆经过A(-2,2),B(6,0)两点,圆心M在直线2x-y=1上,
求该圆的方程.
待定系数法是求曲线方程常用的一种方法.
课本例题
例2 已知某圆经过A(-2,2),B(6,0)两点,圆心M在直线2x-y=1上,
求该圆的方程.
课本例题
已知某圆圆心C在x轴上,半径为10,且在y轴上截得的线段AB的长为16,则圆的标准方程为________.
易错警示 求圆的标准方程
错因分析
(x+6)2+y2=100
错解分析:错误的根本原因是借助图形辅助求解时漏掉一解,以及对圆的标准方程的结构形式特点掌握不准确导致错误.
错因分析
错因分析
防范措施:
1.突出图形的作用
图形可以帮助我们直观地分析题意,能有效地避免漏解,提高解题的准确性.如本题通过图形能准确地判定出圆心在y轴左右两侧这两种情形,忽略此点易造成漏解.
2.准确认识圆的标准方程的结构特点
圆的标准方程的结构特点是:等号左边是平方和的形式,右边是半径的平方而非半径.
如本题中若不注意此点则易出现类似(x±6)2+y2=10的失误.
错因分析
题型1 用直接法求圆的标准方程
典例剖析
用直接法求圆的标准方程的策略
(1)首先求出圆心坐标和半径,然后直接写出圆的标准方程.
(2)确定圆心和半径时,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“过切点与切线垂直的直线必过圆心”等.
提醒:当圆与坐标轴相切时要特别注意圆心的坐标与圆的半径的关系.
归纳总结
经过点A(-1,3),B(4,2)且圆心在x轴上的圆的方程是________________.
典例剖析
题型2 用待定系数法求圆的标准方程
(x-1)2+y2=13
1.待定系数法求圆的标准方程的一般步骤
设方程
列方程组
解方程组
得方程
设所求圆的方程为(x-a)2+(y-b)2=r2
由已知条件,建立关于a,b,r
解方程组,求出a,b,r
将a,b,r代入所设方程,得所求原方程
如图,已知两点P1(4,9)和P2(6,3).
(1)求以P1P2为直径的圆的方程;
(2)试判断点M(6,9),N(3,3),Q(5,3)是在圆上、在圆内、还是在圆外.
题型3 点与圆的位置关系
典例剖析
归纳总结
判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:主要是把点的坐标代入圆的标准方程来判断:
点P(x0,y0)在圆C上 (x0-a)2+(y0-b)2=r2;
点P(x0,y0)在圆C内 (x0-a)2+(y0-b)2
分层练习-基础
1.以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )
A.(x-1)2+(y-2)2=25 B.(x+1)2+(y+2)2=25
C.(x+1)2+(y+2)2=100 D.(x-1)2+(y-2)2=100
A
D
分层练习-基础
3.点P(m,5)与圆x2+y2=24的位置关系是( )
A.在圆外 B.在圆内
C.在圆上 D.不确定
A
A
分层练习-基础
5.一圆与圆C:(x+2)2+(y+1)2=3为同心圆且面积为圆C面积的两倍,此圆的标准方程为 .
8.过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=________.
(x+2)2+(y+1)2=6
(x+1)2+y2=2
或(x+3)2+y2=2
(x-2)2+y2=9
分层练习-巩固
9.已知A(0,1),B(2,1),C(3,4),D(-1,2),问这四点能否在同一个圆上?为什么?
分层练习-巩固
11.已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆上,求a的值;
(2)已知点P(3,3)和点Q(5,3),线段PQ(不含端点)与圆N有且只有一个公共点,求a的取值范围.
分层练习-巩固
12.如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
分层练习-拓展
12.如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
分层练习-巩固
圆的标准方程:
圆心为C(a,b),半径为r的圆的方程:
点与圆的位置关系的判断:
课堂小结
圆上的点到定点的最值:
同课章节目录
