湘教版高中数学选择性必修第一册第3章圆锥曲线与方程3.2.2课时2双曲线简单几何性质的应用课件(共50张PPT)
文档属性
| 名称 | 湘教版高中数学选择性必修第一册第3章圆锥曲线与方程3.2.2课时2双曲线简单几何性质的应用课件(共50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 11:51:21 | ||
图片预览











文档简介
(共50张PPT)
第3章 圆锥曲线与方程
3.2 双曲线
3.2.2 双曲线的简单几何性质
课时2 双曲线简单几何性质的应用
1.进一步掌握双曲线的方程及其几何性质的应用,会判断直线与双曲线的位置关系.(逻辑推理)
2.能运用直线与双曲线的位置关系解决相关的弦长、中点弦问题.(数学运算)
1.前面我们学习了双曲线的方程、简单几何性质,你能写出双曲线的标准方程及性质吗?
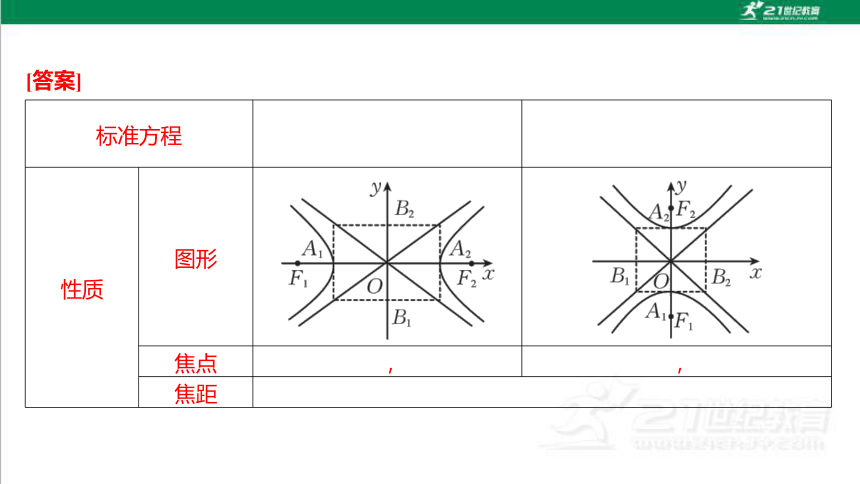
[答案]
标准方程
性质 图形
焦点 , ,
焦距
标准方程
性质 范围 或 , 或 ,
对称性 对称轴:坐标轴对称中心:
顶点 , ,
轴 实轴:线段 ,长为 .虚轴:线段 ,长为 .实半
轴长为 ,虚半轴长为
离心率
渐近线
续表
2.若直线与圆(椭圆)有且只有一个公共点,则直线与圆(椭圆)相切.那么直线与双曲线相切能用这个方法判断吗?
[答案] 不能.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)若直线与双曲线只有一个公共点,则直线与双曲线相切.( )
×
(2)若直线与双曲线的一条渐近线平行,则该直线与双曲线有两个交点.( )
×
CD
A.1 B.2 C.3 D.4
C
探究1 直线与双曲线的位置关系
问题1: 若直线和双曲线只有一个公共点,则直线和双曲线一定相切吗?
[答案] 可能相切,也可能相交,当直线和渐近线平行时,直线和双曲线相交且只有一个交点.
[答案] 四条,其中有两条切线,两条和渐近线平行的直线.
问题3: 判断直线与双曲线的位置关系要注意什么?
[答案] (1)联立直线方程与双曲线方程,消元后得到的方程不一定是一元二次方程,也可能是一次方程,这时,直线一定与双曲线的渐近线平行.(2)直线与双曲线只有一个公共点时,直线不一定与双曲线相切,也可能相交,这时,直线一定与双曲线的渐近线平行.
新知生成
位置关系 公共点 判定方法
相交 1个或2个 或
相切 1个 且
相离 0个 且
新知运用
(1)有两个公共点?
(2)有一个公共点?
(3)没有公共点?
方法指导 要研究直线与双曲线的交点个数,通常需联立直线与双曲线方程组成方程组,消去方程组中的一个变量,得到关于另一个变量的一元二次方程或一元一次方程,再对方程解的个数进行讨论.
探究2 与双曲线有关的弦长及中点弦问题
问题2: 椭圆中点弦问题常用什么方法解决?双曲线中点弦问题能用这种方法吗?
[答案] 涉及椭圆中点弦问题常用点差法或根与系数的关系解决,此法也能用在双曲线中点弦问题中.
新知生成
解决与双曲线有关的中点弦问题的方法
第一种方法:联立消元法,即联立直线和双曲线的方程,借助于一元二次方程的根的判别式、根与系数的关系、中点坐标公式及参数法求解.
第二种方法:点差法,根据双曲线弦中点的性质,求出直线的斜率,再用点斜式得出直线方程.
特别提醒:中点弦问题中判断点的位置非常重要.
新知运用
&2& 中点弦问题:可以联立方程组消元后,用判别式和中点坐标公式求解;也可以用点差法和中点坐标公式求解.注意都需要检验.
探究3 双曲线性质的综合应用
问题1: 双曲线与椭圆有哪些不同点?
[答案] 双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率
, , 的关系
问题2: 双曲线常与哪些知识结合命题?
[答案] 双曲线常与向量、直线等知识结合命题.
新知生成
与双曲线有关的综合问题
(1)当与向量知识结合时,注意运用向量的坐标运算,将向量间的关系转化为点的坐标问题,再根据根与系数的关系,将所求问题与条件建立联系求解.
(2)当与直线知识结合时,常常联立直线与双曲线的方程,消元后当二次项的系数不为0时,常常利用一元二次方程的根的判别式、根与系数的关系构造相关数量关系求解;当二次项系数为0时,直接分析求解.
新知运用
&3& 解决与双曲线有关的综合问题,常需要挖掘出题目中隐含的数量关系、垂直关系等,然后利用方程根与系数的关系构造等式或函数关系式进行合理的转化,这其中要注意利用根的判别式来确定参数的限制条件.
A
B
第3章 圆锥曲线与方程
3.2 双曲线
3.2.2 双曲线的简单几何性质
课时2 双曲线简单几何性质的应用
1.进一步掌握双曲线的方程及其几何性质的应用,会判断直线与双曲线的位置关系.(逻辑推理)
2.能运用直线与双曲线的位置关系解决相关的弦长、中点弦问题.(数学运算)
1.前面我们学习了双曲线的方程、简单几何性质,你能写出双曲线的标准方程及性质吗?
[答案]
标准方程
性质 图形
焦点 , ,
焦距
标准方程
性质 范围 或 , 或 ,
对称性 对称轴:坐标轴对称中心:
顶点 , ,
轴 实轴:线段 ,长为 .虚轴:线段 ,长为 .实半
轴长为 ,虚半轴长为
离心率
渐近线
续表
2.若直线与圆(椭圆)有且只有一个公共点,则直线与圆(椭圆)相切.那么直线与双曲线相切能用这个方法判断吗?
[答案] 不能.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)若直线与双曲线只有一个公共点,则直线与双曲线相切.( )
×
(2)若直线与双曲线的一条渐近线平行,则该直线与双曲线有两个交点.( )
×
CD
A.1 B.2 C.3 D.4
C
探究1 直线与双曲线的位置关系
问题1: 若直线和双曲线只有一个公共点,则直线和双曲线一定相切吗?
[答案] 可能相切,也可能相交,当直线和渐近线平行时,直线和双曲线相交且只有一个交点.
[答案] 四条,其中有两条切线,两条和渐近线平行的直线.
问题3: 判断直线与双曲线的位置关系要注意什么?
[答案] (1)联立直线方程与双曲线方程,消元后得到的方程不一定是一元二次方程,也可能是一次方程,这时,直线一定与双曲线的渐近线平行.(2)直线与双曲线只有一个公共点时,直线不一定与双曲线相切,也可能相交,这时,直线一定与双曲线的渐近线平行.
新知生成
位置关系 公共点 判定方法
相交 1个或2个 或
相切 1个 且
相离 0个 且
新知运用
(1)有两个公共点?
(2)有一个公共点?
(3)没有公共点?
方法指导 要研究直线与双曲线的交点个数,通常需联立直线与双曲线方程组成方程组,消去方程组中的一个变量,得到关于另一个变量的一元二次方程或一元一次方程,再对方程解的个数进行讨论.
探究2 与双曲线有关的弦长及中点弦问题
问题2: 椭圆中点弦问题常用什么方法解决?双曲线中点弦问题能用这种方法吗?
[答案] 涉及椭圆中点弦问题常用点差法或根与系数的关系解决,此法也能用在双曲线中点弦问题中.
新知生成
解决与双曲线有关的中点弦问题的方法
第一种方法:联立消元法,即联立直线和双曲线的方程,借助于一元二次方程的根的判别式、根与系数的关系、中点坐标公式及参数法求解.
第二种方法:点差法,根据双曲线弦中点的性质,求出直线的斜率,再用点斜式得出直线方程.
特别提醒:中点弦问题中判断点的位置非常重要.
新知运用
&2& 中点弦问题:可以联立方程组消元后,用判别式和中点坐标公式求解;也可以用点差法和中点坐标公式求解.注意都需要检验.
探究3 双曲线性质的综合应用
问题1: 双曲线与椭圆有哪些不同点?
[答案] 双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率
, , 的关系
问题2: 双曲线常与哪些知识结合命题?
[答案] 双曲线常与向量、直线等知识结合命题.
新知生成
与双曲线有关的综合问题
(1)当与向量知识结合时,注意运用向量的坐标运算,将向量间的关系转化为点的坐标问题,再根据根与系数的关系,将所求问题与条件建立联系求解.
(2)当与直线知识结合时,常常联立直线与双曲线的方程,消元后当二次项的系数不为0时,常常利用一元二次方程的根的判别式、根与系数的关系构造相关数量关系求解;当二次项系数为0时,直接分析求解.
新知运用
&3& 解决与双曲线有关的综合问题,常需要挖掘出题目中隐含的数量关系、垂直关系等,然后利用方程根与系数的关系构造等式或函数关系式进行合理的转化,这其中要注意利用根的判别式来确定参数的限制条件.
A
B
同课章节目录
