2025年辽宁省抚顺市新宾县白家中学中考数学模拟试卷(4月份)(含部分答案)
文档属性
| 名称 | 2025年辽宁省抚顺市新宾县白家中学中考数学模拟试卷(4月份)(含部分答案) |  | |
| 格式 | docx | ||
| 文件大小 | 404.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-27 22:58:19 | ||
图片预览




文档简介
2025年辽宁省抚顺市新宾县白家中学中考数学模拟试卷(4月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一个几何体如图水平放置,它的俯视图是( )
A. B. C. D.
2.古筝是中国独特的民族乐器之一,为了保持音准,弹奏者常使用调音器对每根琴弦进行调音.如图所示是某古筝调音器软件的界面,指针指向40表示音调偏高,需放松琴弦.下列指针指向的数字中表示需拧紧琴弦,且最接近标准音(指针指在0处为标准音)的是( )
A. 10
B. 20
C. -25
D. -5
3.下列食品标识图中,依次表示绿色饮品、绿色食品、有机食品和速冻食品,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.近年来,我国科学家在多个领域探索人工智能驱动的科学研究,其中“人工智能辅助的基因组选择”能在几周内分析上百万基因型,有效开发全球植物种质库里超700万份种质资源,极大提升了育种流程效率和精度,应用潜力巨大.其中数据“700万”用科学记数法表示为( )
A. 0.7×106 B. 7×105 C. 7×106 D. 7×107
5.下列算式计算正确的是( )
A. x+x2=x3 B. x5 x3=x15 C. -x3-(-x)3=0 D. -x(x-1)=-x2
6.如图,在平行四边形ABCD中,∠D=60°.以点B为圆心、AB的长为半径作弧交边BC于点E,连接AE;分别以点A,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AE于点O,交边AD于点F,若AB=4,则OF的长是( )
A. 2 B. C. 4 D.
7.已知一个袋子中装有5个红球,x个黑球,10个白球,这些球除颜色外其余都相同.若从袋子中摸出一个黑球和一个白球后(不放回),再摸出一个球是红球的概率为,则x等于( )
A. 1 B. 2 C. 3 D. 5
8.中国古代数学著作《九章算术》第七章主要内容是“盈不足术”,其中有这样一道盈亏类问题:“今有共买羊,人出五,不足九十;人出五十,适足.问人数、羊价各几何?”题目大意是:“有几个人共同购买一只羊,若每人出五元,还差九十元;若每人出五十元,刚好够.问有几个人,羊的价格是多少?”设有x人,羊的价格为y元,可列方程组为( )
A. B. C. D.
9.如图,正方形ABCD的对角线AC与BD相交于点O,点E在OB上,且BE=OE,连接CE并延长交DA的延长线于点F,则AF:FD的值为( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
10.如图,已知点M的坐标为(5,5),N为x轴正半轴上一点,且点N的横坐标大于5,直线MN绕点M顺时针旋转45°交y轴于点L,连接NL,当NL=OL+3时,点N的坐标为( )
A. (6,0)
B. (7,0)
C. (8,0)
D. (9,0)
二、填空题:本题共5小题,每小题3分,共15分。
11.分解因式:m2-9n2=______.
12.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=155°,∠2=30°,则∠3的大小是______.
13.如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为______.
14.在平面直角坐标系中,已知点A的坐标为(-1,0),点B的坐标为(0,2),AB是等腰直角三角形ABC的一条直角边;且点C位于第一象限,若抛物线y=ax2-x+1与直线AC有两个不同的交点,则a的取值范围是______.
15.如图,在矩形ABCD中,AB=10,AD=14,点E在边AD上,且DE=4,F是边AB上一动点,沿EF将△AEF翻折,点A翻折后落在A'点,连接A'B,A'C.若△A′BC的面积为28,则AF的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
计算:
(1)|-2|--;
(2)(x-)÷(1-).
17.(本小题8分)
西藏日喀则地震期间,政府急需将一批医疗物资运往灾区,某车队打算用A,B两种货车来运送这批医疗物资.已知A种货车比B种货车每辆多装40件医疗物资,且A种货车装运1200件医疗物资所用的车辆数与B种货车装运1000件医疗物资所用的车辆数相等.
(1)求A,B两种货车每辆可装多少件医疗物资;
(2)现有A、B两种货车共10辆,要运送2200件医疗物资,求至少需要A种货车多少辆.
18.(本小题8分)
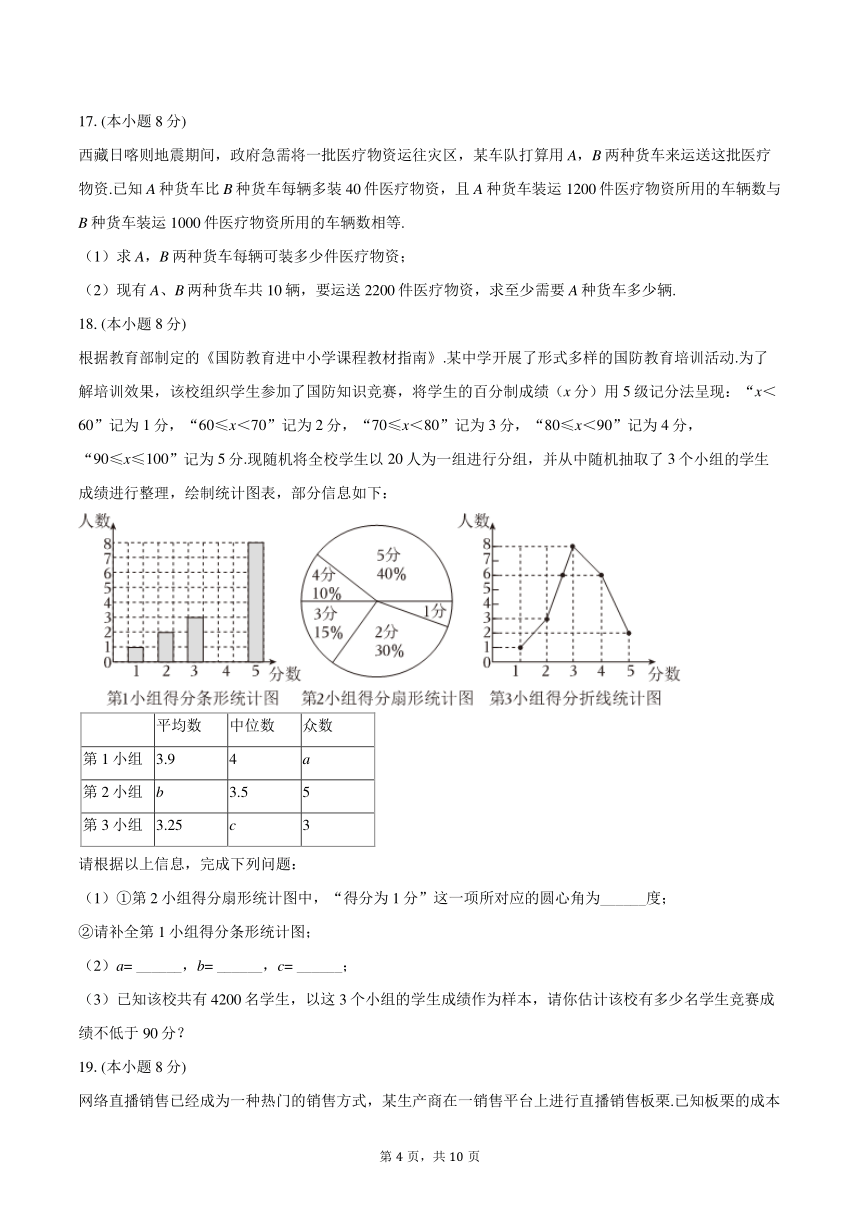
根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为______度;
②请补全第1小组得分条形统计图;
(2)a= ______,b= ______,c= ______;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
19.(本小题8分)
网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/千克,每日销售量y(千克)与销售单价x(元)之间满足一次函数关系,有关数据如下表,设公司销售板栗的日获利为w(元).
x/元 7 8 9
y/千克 2700 2600 2500
(1)求每日销售量y与销售单价x之间的函数关系式.(不用写自变量的取值范围)
(2)若销售单价不高于12元,当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少?
20.(本小题8分)
“1”腔热血护家园,“1”呼百应齐参与,“9”久守护永不变,在“全国消防日”之际,学校组织学生到消防队参观消防救援车实施救援演练的过程,图1是高空救援消防车实物图,图2是其侧面示意图,操作面OD与水平地面HG平行,操作面离地面的距离OH=1米,伸缩臂CO可绕着点O旋转,点A在OD上,AB为云梯的液压杆,其中AB可伸缩,已知套管OB=3米,且套管OB的长度不变.消防员为大家介绍:此时,∠AOB=30°,∠BAD=60°,CE⊥HG于点E,交OD于点F,云梯末端工作台C上升到了离地面CE=5.5米的高处.
(1)求此时液压杆AB的长度;(结果保留根号)
(2)通过消防员的操作,云梯伸缩臂CO绕点O逆时针旋转23°并伸长至OC',云梯末端工作台C的铅锤高度上升了4米至C',请问伸缩臂OC'比伸缩臂OC伸长了多少米?
(参考数据:sin53°≈0.8,cos53°≈0.6,结果精确到0.1)
21.(本小题8分)
如图,以△ABC的边AB为直径作⊙O分别交AC,BC于点D,E,过点E作EF⊥AC,垂足为F,FE的延长线与AB的延长线交于点G,E是劣弧BD的中点.
(1)求证:EF为⊙O的切线.
(2)若AF=4,AB=6,求BG的长.
22.(本小题12分)
截长补短是初中数学几何题中一种辅助线的添加方法,这种方法常用于证明两条短线段之和等于第三条长线段.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
例如:如图1,△ABC,△ADE都是等边三角形,EC与BD交于点F,连接FA,探究FA、FB、FC之间的数量关系.
思路梳理:
截长法:易证△BAD≌△CAE,∴∠ABD=∠ACE.易得∠CFB=60°.在线段FB上截取FG=FC,则可求得FA,FB,FC之间的数量关系为FB=FA+FC.
补短法:易证△BAD≌△CAE,∴∠ABD=∠ACE.易得∠CFB=60°.在FC的延长线上截取FH=FB,连接BH,则可求得FA,FB,FC之间的数量关系为FB=FA+FC.
(1)如图2,△ABC是等边三角形,D为线段BC上任意一点,连接AD,E为AB延长线上一点,且BE=CD,F为CB延长线上一点,且∠FAD=60°请猜想线段AF,EF,AD之间存在的数量关系,并说明理由.
(2)如图3,在Rt△ABC中,∠BAC=90°,AB=AC,若D是边BC下方一点,∠BDC=90°,探索线段AD,BD,CD之间的数量关系,并说明理由.
(3)如图4,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,D为AB边的中点,连接CD,过点A作AF⊥CD于点E,交BC于点F,连接DF.
①请猜想线段DC,FA,FD之间的数量关系,并说明理由;
②若AB=6,则FD的长为______.
23.(本小题13分)
在平面直角坐标系中,对“纵横值”给出如下定义:点A(x,y)是函数图象上任意一点,纵坐标y与横坐标x的差“y-x”称为点A的“纵横值”.函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”,最小值称为函数的“最劣纵横值”.例如:点A(1、3)在函数y=2x+1(3≤x≤6)的图象上,点A的“纵横值”为3-1=2,函数y=2x+1图象上所有点的“纵横值”可以表示为y-x=2x+1-x=x+1,当3≤x≤6时,x+1的最大值为6+1=7,最小值为3+1=4,所以函数y=2x+1(3≤x≤6)的“最优纵横值”为7,“最劣纵横值”为4.
(1)点P(-2,4)的“纵横值”为______.
(2)已知二次函数y=-x2+7x+1,当-2≤x≤4时,求它的“最优纵横值”和“最劣纵横值”.
(3)若二次函数y=ax2+2ax+c(a<0)的图象顶点在“纵横值”为5的函数图象上.
①二次函数y=ax2+2ax+c的“最优纵横值”为,求该二次函数的表达式.
②当a+1≤x≤a+3时,设二次函数y=ax2+(2a+1)x+c(a<0)的“最优纵横值”为t1,“最劣纵横值”为t2,且t2-t1=2a,求a的值.
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】(m+3n)(m-3n)
12.【答案】55°
13.【答案】16
14.【答案】且a≠0
15.【答案】
16.【答案】2-; x-1.
17.【答案】A种货车每辆可装240件医疗物资,B种货车每辆可装200件医疗物资;
至少需要A种货车5辆.
18.【答案】①18;②详见解答;
5,3.5,3;
1260名.
19.【答案】y=-100x+3400; 当销售单价定为12元时,销售这种板栗日获利w最大,最大利润为13200元.
20.【答案】解:(1)作BM⊥OD于点M,
∴∠BMO=90°,
∵∠AOB=30°,OB=3米,
∴BM=OB=(米),
∵∠BAD=60°,
∴AB==(米).
答:液压杆AB的长度为米;
(2)作C′N⊥OD于点N,
∴∠C′NO=90°,
∵CE=5.5米,OH=1米,
∴CF=5.5-1=4.5(米),
∵CE⊥HG,OD∥HG,
∴CE⊥OD,
∴∠OFC=90°,
∵∠AOB=30°,
∴CO=2CF=9(米),
∵云梯末端工作台C的铅锤高度上升了4米至C',
∴C′N=4.5+4=8.5(米),
由题意得:∠COC′=23°,
∴∠NOC′=53°,
∴OC′=≈8.5÷0.8=10.625(米),
∴OC′-OC=10.625-9≈1.6(米).
答:伸缩臂OC'比伸缩臂OC伸长了约1.6米.
21.【答案】证明见解答;
BG的长为6.
22.【答案】AF=AD+EF,理由见解答;
CD+BD=AD,理由见解答;
①DC=FA+FD,理由见解答;
②.
23.【答案】6;
函数“最优纵横值”为10,“最劣纵横值”为-15;
①y=-x2-2x+3;
②a的值为或.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一个几何体如图水平放置,它的俯视图是( )
A. B. C. D.
2.古筝是中国独特的民族乐器之一,为了保持音准,弹奏者常使用调音器对每根琴弦进行调音.如图所示是某古筝调音器软件的界面,指针指向40表示音调偏高,需放松琴弦.下列指针指向的数字中表示需拧紧琴弦,且最接近标准音(指针指在0处为标准音)的是( )
A. 10
B. 20
C. -25
D. -5
3.下列食品标识图中,依次表示绿色饮品、绿色食品、有机食品和速冻食品,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.近年来,我国科学家在多个领域探索人工智能驱动的科学研究,其中“人工智能辅助的基因组选择”能在几周内分析上百万基因型,有效开发全球植物种质库里超700万份种质资源,极大提升了育种流程效率和精度,应用潜力巨大.其中数据“700万”用科学记数法表示为( )
A. 0.7×106 B. 7×105 C. 7×106 D. 7×107
5.下列算式计算正确的是( )
A. x+x2=x3 B. x5 x3=x15 C. -x3-(-x)3=0 D. -x(x-1)=-x2
6.如图,在平行四边形ABCD中,∠D=60°.以点B为圆心、AB的长为半径作弧交边BC于点E,连接AE;分别以点A,E为圆心,大于的长为半径作弧,两弧交于点P,作射线BP交AE于点O,交边AD于点F,若AB=4,则OF的长是( )
A. 2 B. C. 4 D.
7.已知一个袋子中装有5个红球,x个黑球,10个白球,这些球除颜色外其余都相同.若从袋子中摸出一个黑球和一个白球后(不放回),再摸出一个球是红球的概率为,则x等于( )
A. 1 B. 2 C. 3 D. 5
8.中国古代数学著作《九章算术》第七章主要内容是“盈不足术”,其中有这样一道盈亏类问题:“今有共买羊,人出五,不足九十;人出五十,适足.问人数、羊价各几何?”题目大意是:“有几个人共同购买一只羊,若每人出五元,还差九十元;若每人出五十元,刚好够.问有几个人,羊的价格是多少?”设有x人,羊的价格为y元,可列方程组为( )
A. B. C. D.
9.如图,正方形ABCD的对角线AC与BD相交于点O,点E在OB上,且BE=OE,连接CE并延长交DA的延长线于点F,则AF:FD的值为( )
A. 1:2 B. 1:3 C. 2:3 D. 3:4
10.如图,已知点M的坐标为(5,5),N为x轴正半轴上一点,且点N的横坐标大于5,直线MN绕点M顺时针旋转45°交y轴于点L,连接NL,当NL=OL+3时,点N的坐标为( )
A. (6,0)
B. (7,0)
C. (8,0)
D. (9,0)
二、填空题:本题共5小题,每小题3分,共15分。
11.分解因式:m2-9n2=______.
12.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=155°,∠2=30°,则∠3的大小是______.
13.如图,直线AB与反比例函数图象交于A,B两点,与x轴交于点M且满足,连接AO并延长交反比例函数图象于点C,连接BC,若△ABC的面积为24,则k的值为______.
14.在平面直角坐标系中,已知点A的坐标为(-1,0),点B的坐标为(0,2),AB是等腰直角三角形ABC的一条直角边;且点C位于第一象限,若抛物线y=ax2-x+1与直线AC有两个不同的交点,则a的取值范围是______.
15.如图,在矩形ABCD中,AB=10,AD=14,点E在边AD上,且DE=4,F是边AB上一动点,沿EF将△AEF翻折,点A翻折后落在A'点,连接A'B,A'C.若△A′BC的面积为28,则AF的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
计算:
(1)|-2|--;
(2)(x-)÷(1-).
17.(本小题8分)
西藏日喀则地震期间,政府急需将一批医疗物资运往灾区,某车队打算用A,B两种货车来运送这批医疗物资.已知A种货车比B种货车每辆多装40件医疗物资,且A种货车装运1200件医疗物资所用的车辆数与B种货车装运1000件医疗物资所用的车辆数相等.
(1)求A,B两种货车每辆可装多少件医疗物资;
(2)现有A、B两种货车共10辆,要运送2200件医疗物资,求至少需要A种货车多少辆.
18.(本小题8分)
根据教育部制定的《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织学生参加了国防知识竞赛,将学生的百分制成绩(x分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制统计图表,部分信息如下:
平均数 中位数 众数
第1小组 3.9 4 a
第2小组 b 3.5 5
第3小组 3.25 c 3
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角为______度;
②请补全第1小组得分条形统计图;
(2)a= ______,b= ______,c= ______;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生竞赛成绩不低于90分?
19.(本小题8分)
网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/千克,每日销售量y(千克)与销售单价x(元)之间满足一次函数关系,有关数据如下表,设公司销售板栗的日获利为w(元).
x/元 7 8 9
y/千克 2700 2600 2500
(1)求每日销售量y与销售单价x之间的函数关系式.(不用写自变量的取值范围)
(2)若销售单价不高于12元,当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少?
20.(本小题8分)
“1”腔热血护家园,“1”呼百应齐参与,“9”久守护永不变,在“全国消防日”之际,学校组织学生到消防队参观消防救援车实施救援演练的过程,图1是高空救援消防车实物图,图2是其侧面示意图,操作面OD与水平地面HG平行,操作面离地面的距离OH=1米,伸缩臂CO可绕着点O旋转,点A在OD上,AB为云梯的液压杆,其中AB可伸缩,已知套管OB=3米,且套管OB的长度不变.消防员为大家介绍:此时,∠AOB=30°,∠BAD=60°,CE⊥HG于点E,交OD于点F,云梯末端工作台C上升到了离地面CE=5.5米的高处.
(1)求此时液压杆AB的长度;(结果保留根号)
(2)通过消防员的操作,云梯伸缩臂CO绕点O逆时针旋转23°并伸长至OC',云梯末端工作台C的铅锤高度上升了4米至C',请问伸缩臂OC'比伸缩臂OC伸长了多少米?
(参考数据:sin53°≈0.8,cos53°≈0.6,结果精确到0.1)
21.(本小题8分)
如图,以△ABC的边AB为直径作⊙O分别交AC,BC于点D,E,过点E作EF⊥AC,垂足为F,FE的延长线与AB的延长线交于点G,E是劣弧BD的中点.
(1)求证:EF为⊙O的切线.
(2)若AF=4,AB=6,求BG的长.
22.(本小题12分)
截长补短是初中数学几何题中一种辅助线的添加方法,这种方法常用于证明两条短线段之和等于第三条长线段.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
例如:如图1,△ABC,△ADE都是等边三角形,EC与BD交于点F,连接FA,探究FA、FB、FC之间的数量关系.
思路梳理:
截长法:易证△BAD≌△CAE,∴∠ABD=∠ACE.易得∠CFB=60°.在线段FB上截取FG=FC,则可求得FA,FB,FC之间的数量关系为FB=FA+FC.
补短法:易证△BAD≌△CAE,∴∠ABD=∠ACE.易得∠CFB=60°.在FC的延长线上截取FH=FB,连接BH,则可求得FA,FB,FC之间的数量关系为FB=FA+FC.
(1)如图2,△ABC是等边三角形,D为线段BC上任意一点,连接AD,E为AB延长线上一点,且BE=CD,F为CB延长线上一点,且∠FAD=60°请猜想线段AF,EF,AD之间存在的数量关系,并说明理由.
(2)如图3,在Rt△ABC中,∠BAC=90°,AB=AC,若D是边BC下方一点,∠BDC=90°,探索线段AD,BD,CD之间的数量关系,并说明理由.
(3)如图4,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,D为AB边的中点,连接CD,过点A作AF⊥CD于点E,交BC于点F,连接DF.
①请猜想线段DC,FA,FD之间的数量关系,并说明理由;
②若AB=6,则FD的长为______.
23.(本小题13分)
在平面直角坐标系中,对“纵横值”给出如下定义:点A(x,y)是函数图象上任意一点,纵坐标y与横坐标x的差“y-x”称为点A的“纵横值”.函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”,最小值称为函数的“最劣纵横值”.例如:点A(1、3)在函数y=2x+1(3≤x≤6)的图象上,点A的“纵横值”为3-1=2,函数y=2x+1图象上所有点的“纵横值”可以表示为y-x=2x+1-x=x+1,当3≤x≤6时,x+1的最大值为6+1=7,最小值为3+1=4,所以函数y=2x+1(3≤x≤6)的“最优纵横值”为7,“最劣纵横值”为4.
(1)点P(-2,4)的“纵横值”为______.
(2)已知二次函数y=-x2+7x+1,当-2≤x≤4时,求它的“最优纵横值”和“最劣纵横值”.
(3)若二次函数y=ax2+2ax+c(a<0)的图象顶点在“纵横值”为5的函数图象上.
①二次函数y=ax2+2ax+c的“最优纵横值”为,求该二次函数的表达式.
②当a+1≤x≤a+3时,设二次函数y=ax2+(2a+1)x+c(a<0)的“最优纵横值”为t1,“最劣纵横值”为t2,且t2-t1=2a,求a的值.
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】(m+3n)(m-3n)
12.【答案】55°
13.【答案】16
14.【答案】且a≠0
15.【答案】
16.【答案】2-; x-1.
17.【答案】A种货车每辆可装240件医疗物资,B种货车每辆可装200件医疗物资;
至少需要A种货车5辆.
18.【答案】①18;②详见解答;
5,3.5,3;
1260名.
19.【答案】y=-100x+3400; 当销售单价定为12元时,销售这种板栗日获利w最大,最大利润为13200元.
20.【答案】解:(1)作BM⊥OD于点M,
∴∠BMO=90°,
∵∠AOB=30°,OB=3米,
∴BM=OB=(米),
∵∠BAD=60°,
∴AB==(米).
答:液压杆AB的长度为米;
(2)作C′N⊥OD于点N,
∴∠C′NO=90°,
∵CE=5.5米,OH=1米,
∴CF=5.5-1=4.5(米),
∵CE⊥HG,OD∥HG,
∴CE⊥OD,
∴∠OFC=90°,
∵∠AOB=30°,
∴CO=2CF=9(米),
∵云梯末端工作台C的铅锤高度上升了4米至C',
∴C′N=4.5+4=8.5(米),
由题意得:∠COC′=23°,
∴∠NOC′=53°,
∴OC′=≈8.5÷0.8=10.625(米),
∴OC′-OC=10.625-9≈1.6(米).
答:伸缩臂OC'比伸缩臂OC伸长了约1.6米.
21.【答案】证明见解答;
BG的长为6.
22.【答案】AF=AD+EF,理由见解答;
CD+BD=AD,理由见解答;
①DC=FA+FD,理由见解答;
②.
23.【答案】6;
函数“最优纵横值”为10,“最劣纵横值”为-15;
①y=-x2-2x+3;
②a的值为或.
第1页,共1页
同课章节目录
