2.1《数列的概念与简单表示法》(上)
文档属性
| 名称 | 2.1《数列的概念与简单表示法》(上) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-04 12:10:58 | ||
图片预览






文档简介
课件23张PPT。第二章 数 列2.1 数列的概念与简单表示法(上)
高中数学老师欧阳文丰制作学习目标1. 理解数列的概念;
2. 掌握数列简单的几种表示方法;
3. 了解数列是一种特殊的函数。目标达成1.通过数学文化、生活实例感知数列;
2.通过自主学习、探究性学习达成目标。 传说古希腊毕达哥拉斯学派数学家研究的问题:
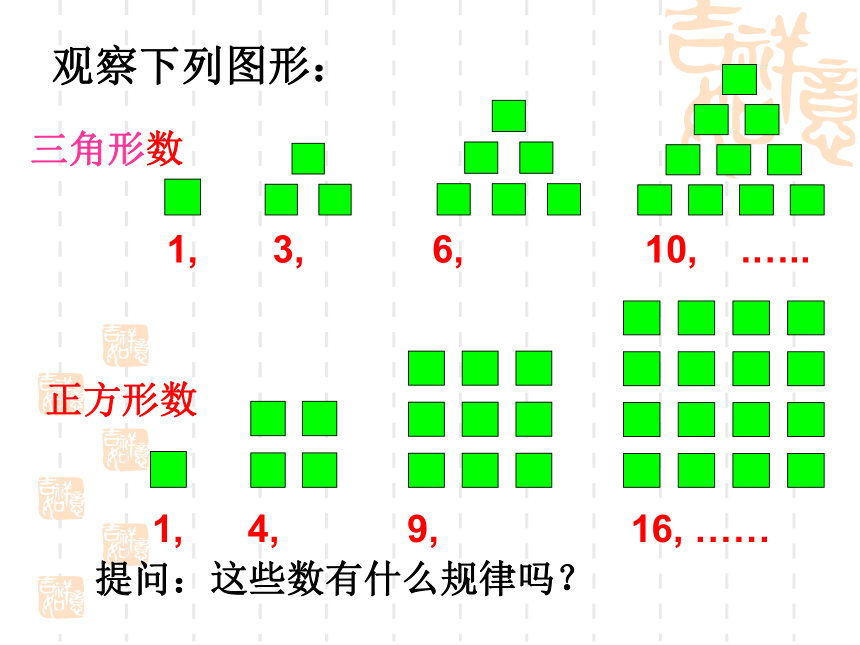
三角形数:1,3,6,10,···
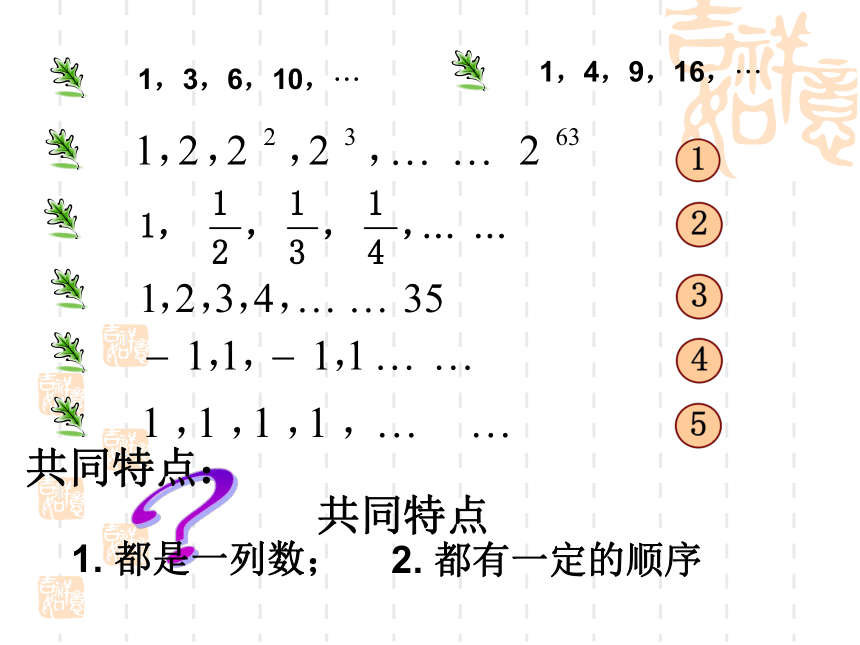
正方形数:1,4,9,16,···事 例 :三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……观察下列图形:提问:这些数有什么规律吗?1740,1823,1906,1989,2072,…2,4,8,16,32,…15,5,16,16,28,32,51 人们在1740年发现了一颗彗星,并推算出它每隔83年出现一次,则从出现那次算起,这颗彗星出现的年份依次为: 1984年到2008年,我国体育健儿共参加了7次奥运会,获得的金牌数依次为: 某种细胞,如果每个细胞每分钟分裂为2个,那么每过一分钟,一个细胞分裂的个数依次为:再来看几个问题:?共同特点共同特点:1. 都是一列数;2. 都有一定的顺序1,3,6,10,···1,4,9,16,···定义:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)12数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
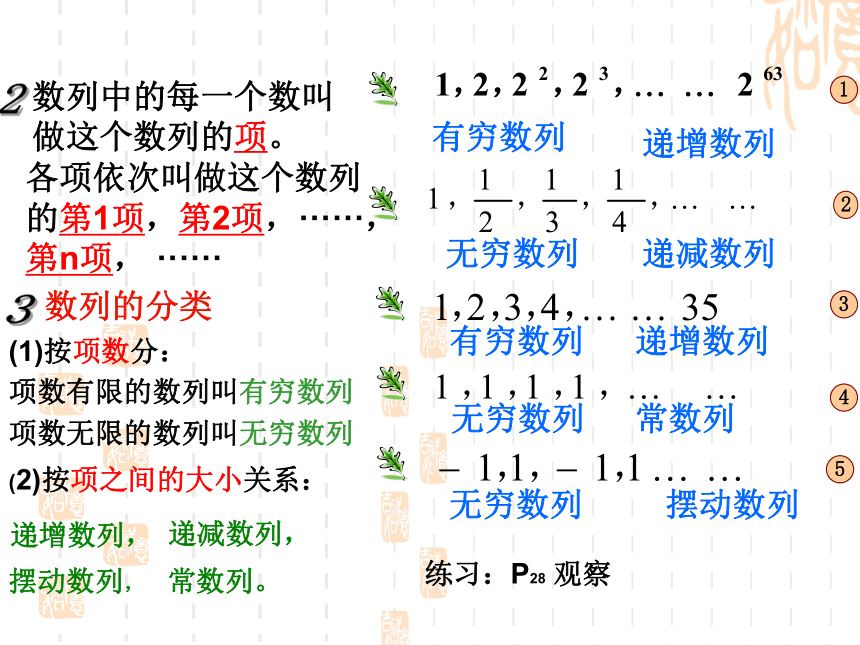
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列练习:P28 观察⑴全体自然数构成数列:0,1,2,3, … . ⑵1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.⑶无穷多个3构成数列:
3,3,3,3,3, … .⑷目前通用的人民币面额从大到小的顺序构成数列
(单位:元)
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.⑸-1的1次幂, 2次幂, 3次幂, 4次幂……构成数列
-1,1,-1,1, … .递增数列递减数列常数列递增数列摆动数列观察4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 例1:设某一数列的通项公式为高一(6)班考试名次由小到大排成的一列数例2每个序号也都对应着一个数(项)序号项 从函数的观点看,
是 的函数。
y=f(x)ann函数值自变量 从映射的观点看,数列可以看作是: 到 的映射数列项
序号数列项序号 (正整数或它的有限子集)项6数列的实质序号项即,数列可以看作是一个定义域为正整数集
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。序号通项公式1234567891024681012141618200是些孤立点-17数列用图象表示时的特点——一群孤立的点 例2 :图2.1-5中的三角形称为希尔宾斯基(Sierpinski)三角形。在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n达标测评1.根据数列的通项公式填表:2.已知数列{an}满足 写出它的前5项 4. 数列的前5项分别是下列各数,写出一个通项公式,……………………………………
本节课学习的主要内容有:1、数列的有关概念2、数列的通项公式;3、数列的实质; 4、本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2)会用观察法由数列的前几项求数列的通项公式。1.作业本:课本第33页2、4
2.《名师一号》21页自测5分钟
3.思考:课本34页B组第3题作 业补充练习
高中数学老师欧阳文丰制作学习目标1. 理解数列的概念;
2. 掌握数列简单的几种表示方法;
3. 了解数列是一种特殊的函数。目标达成1.通过数学文化、生活实例感知数列;
2.通过自主学习、探究性学习达成目标。 传说古希腊毕达哥拉斯学派数学家研究的问题:
三角形数:1,3,6,10,···
正方形数:1,4,9,16,···事 例 :三角形数1, 3, 6, 10, .….. 正方形数1, 4, 9, 16, ……观察下列图形:提问:这些数有什么规律吗?1740,1823,1906,1989,2072,…2,4,8,16,32,…15,5,16,16,28,32,51 人们在1740年发现了一颗彗星,并推算出它每隔83年出现一次,则从出现那次算起,这颗彗星出现的年份依次为: 1984年到2008年,我国体育健儿共参加了7次奥运会,获得的金牌数依次为: 某种细胞,如果每个细胞每分钟分裂为2个,那么每过一分钟,一个细胞分裂的个数依次为:再来看几个问题:?共同特点共同特点:1. 都是一列数;2. 都有一定的顺序1,3,6,10,···1,4,9,16,···定义:按一定顺序排列着的一列数称为数列问1:数列 ,2 , 改为13 ,… ,35 , 2 , ,… ,3531请问:是不是同一数列?问2:数列改为:-1,1,-1,1……1,-1,1,-1……,请问:是不是同一数列?不是不是(数列具有有序性)12数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项,第2项,······,第n项, ······
3数列的分类(1)按项数分:项数有限的数列叫有穷数列项数无限的数列叫无穷数列(2)按项之间的大小关系:递增数列,递减数列,摆动数列,常数列。有穷数列无穷数列有穷数列无穷数列无穷数列递增数列递增数列递减数列摆动数列常数列练习:P28 观察⑴全体自然数构成数列:0,1,2,3, … . ⑵1996~2002年某市普通高中生人数(单位:万人)构成数列:82,93,105,119,129,130,132.⑶无穷多个3构成数列:
3,3,3,3,3, … .⑷目前通用的人民币面额从大到小的顺序构成数列
(单位:元)
100,50,20,10,5,2,1,0.5,0.2,0.1,0.05,0.02,0.01.⑸-1的1次幂, 2次幂, 3次幂, 4次幂……构成数列
-1,1,-1,1, … .递增数列递减数列常数列递增数列摆动数列观察4 数列的一般形式可以
写成:简记为 其中是数第1项第2项第3项第n项5 的第n项
与项数之间的关系可以用一个公式来表示,列的第n项。??? 那么这个公式就叫做这个数列的通项公式。如果数列或??思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 例1:写出下面数列的一个通项公式,使它的前4项分别是下列各数:注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 思 考 :根据数列的前若干项写出的通项公式的形式唯一吗?请举例说明。? 注意:①一些数列的通项公式不是唯一的②不是每一个数列都能写出它的通项公式③ 例1:设某一数列的通项公式为高一(6)班考试名次由小到大排成的一列数例2每个序号也都对应着一个数(项)序号项 从函数的观点看,
是 的函数。
y=f(x)ann函数值自变量 从映射的观点看,数列可以看作是: 到 的映射数列项
序号数列项序号 (正整数或它的有限子集)项6数列的实质序号项即,数列可以看作是一个定义域为正整数集
( 或它的有限子集{1,2,…,n})的函数,当自变量从小到大依 次取值时对应的一列函数值。序号通项公式1234567891024681012141618200是些孤立点-17数列用图象表示时的特点——一群孤立的点 例2 :图2.1-5中的三角形称为希尔宾斯基(Sierpinski)三角形。在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n达标测评1.根据数列的通项公式填表:2.已知数列{an}满足 写出它的前5项 4. 数列的前5项分别是下列各数,写出一个通项公式,……………………………………
本节课学习的主要内容有:1、数列的有关概念2、数列的通项公式;3、数列的实质; 4、本节课的能力要求是:(1) 会由通项公式 求数列的任一项;(2)会用观察法由数列的前几项求数列的通项公式。1.作业本:课本第33页2、4
2.《名师一号》21页自测5分钟
3.思考:课本34页B组第3题作 业补充练习
